轮图和联图对应图构形的特征多项式
高瑞梅, 杨文金, 代 群
(1. 长春理工大学 理学院, 长春 130022; 2. 北京工业大学 信息学部, 北京 100124)
0 引 言
超平面构形是一类具有非孤立奇点的超曲面, 是有限维向量空间中有限个超平面形成的集合. 超平面构形在组合学、代数学、代数组合学、拓扑学等领域应用广泛[1]. 目前, 构形的研究主要集中于构形自由性理论的Terao猜想及复空间中构形余集的拓扑性质等问题上[2-6]. 研究表明, 构形的Orlik Soloman代数的Poincaré多项式, 以及复构形补空间的Betti数都与特征多项式联系密切. 因此, 关于重构形、子空间构形、图构形等的特征多项式也得到广泛关注[7-9].
目前, 构形理论的一个主要研究对象是Coxeter构形, 即Coxeter群的反射超平面构成的集合. 其中Al-1-型Coxeter构形, 即辫构形{xi-xj=0|1≤i 设K是一个域,V是域K上的n维向量空间,V中有限个超平面组成的集合称为一个超平面构形, 简称构形, 记为A. 用L(A)表示A中超平面所有非空交集构成的集合. 对于x,y∈L(A), 如果x⊇y, 则定义x≤y, 即L(A)是反包含关系确定的一个偏序集,L(A)称为A的交叉偏序集. 定义Möbius函数μ:L(A)×L(A)→如下: 1) 如果x∈L(A), 则μ(x,x)=1; 构形A的特征多项式χA(t)定义为 其中μ(x)=μ(V,x). 设G=(V(G),E(G))是简单图, 即不含重边也不含自环的无向图, 其中:V(G)是顶点集;E(G)是边集. 定义 AG={xi-xj=0|(i,j)∈E(G)}, 称AG是G对应的图构形. 若G有n个顶点, 则AG是n维向量空间中的一个中心构形. 定义1[13]设n为一个正整数, 一个n-圈Cn定义为一个包含n个顶点和n条边的图, 且满足下列性质: 将边记为e1,e2,…,en, 顶点记为a1,a2,…,an, 对每个j,ej的端点是aj-1和aj, 其中: 1≤j≤n;a0=an. 定义2[13]由一个n-圈添加一个新的顶点, 并将该顶点与圈的所有n个顶点相连, 得到的图称为n-轮图, 记为Wn. 定义3[13]设n是一个正整数, 一个n-路Pn定义为一个包含n条边和(n+1)个顶点的图, 且满足下列性质: 将边记为e1,e2,…,en, 顶点记为a0,a1,…,an, 对每个j,ej的端点是aj-1和aj, 1≤j≤n. 将图G对应图构形的特征多项式简称为G的特征多项式, 记为χG(t). 引理1[14]设e=(i,j)∈E(G),G-e表示图G去掉边e后的图,G/e表示图G中的边e缩为一点, 再将所得图中的重边用单边代替后得到的图. 3个简单图G,G-e,G/e的特征多项式之间的关系为 χG(t)=χG-e(t)-χG/e(t). 引理2[9]k个n-圈(k≥1,n≥3)简单相连所得图G的特征多项式为 定理1n-轮图Wn(n≥3)的特征多项式为 χWn(t)=t(t-2)[(t-2)n-1+(-1)n]. 证明: 对n利用数学归纳法. 当n=3时, 3-轮图对应的特征多项式为 χW3(t)=t(t-1)(t-2)(t-3)=t(t-2)[(t-2)2+(-1)3]. 假设对(n-1)-轮图, 结论成立. 先考虑n-轮图, 设e为Wn中圈的一条边, 则Wn-e为(n-1)个3-圈简单相连所得的图.Wn/e为(n-1)-轮图. 因此由引理2和归纳假设, 可得 χWn-e(t)=t(t-1)(t-2)n-1, χWn/e(t)=t(t-2)[(t-2)n-2+(-1)n-1]. 再由引理1, 可得 χWn(t)=χWn-e(t)-χWn/e(t)=t(t-2)[(t-2)n-1+(-1)n]. 证毕. 例1由定理1知, 如图1所示的5-轮图的特征多项式为 χW5(t)=t(t-1)(t-2)(t-3)(t2-4t+5). 定义4设G1={V1,E1},G2={V2,E2}均为简单图, 且G1∩G2=Ø. 定义G1与G2的联图G1∨G2的顶点集和边集分别为 V(G1∨G2)=V1∪V2, E(G1∨G2)=E1∪E2∪{(i,j)|i∈V1,j∈V2}. 定义5(m-1)-路与(n-1)-路的联图记为G(m,n). 例2联图G(2,3)如图2所示. 引理3[14]完全图Kn的特征多项式为 χKn(t)=t(t-1)(t-2)…(t-n+1), 简记为t(n). 定理2n-路Pn的特征多项式为 χPn(t)=t(t-1)n. 证明: 对n利用数学归纳法. 当n=1时, 易得 χP1(t)=t(t-1), 结论成立. 假设对(n-1)-路, 结论成立. 下面考虑n-路的情形, 取e=en, 则Pn-e为(n-1)-路和孤立点an的不相交并集,Pn/e为(n-1)-路. 因此由归纳假设, 可得 由引理1知, χPn(t)=χPn-e(t)-χPn/e(t)=t(t-1)n. 证毕. 定理3n-路Pn的特征多项式还可表示为 其中: t(k)=t(t-1)…(t-k+1),k=2,3,…,n+1; B=(1n-1,2n-1,…,(n-1)n-1,nn-1)T. 证明: 由定理2可知, 需先证下列等式成立: 由于式(1)的左右两端都有因式t(t-1), 即需证下列等式成立: 令 f(t)=(t-1)n-1, 由于C=AB, 则A-1C=B, 即 则 由于 deg(f(t))=deg(g(t))=n-1且g(i)=f(i)(i=2,3,…,n+1), 则g(t)=f(t), 结论成立. 例3由定理3可知, 4-路的特征多项式为 χG(t)=t(5)+6t(4)+7t(3)+t(2). 引理4[15]设G1,G2是简单图, 则G1,G2的联图G的特征多项式为 χG(t)=χG1(t)∘χG2(t), 其中“∘”表示t(k)∘t(l)=t(k+l). 由定理3和引理4可得: 定理4联图G(m,n)的特征多项式为 例4联图G(3,4)的特征多项式为1 预备知识
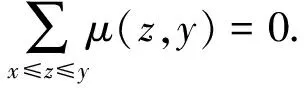
2 主要结果
2.1 轮图对应构形的特征多项式
2.2 联图的特征多项式

