基于现场数据和主元分析的主汽温系统多变量建模

侯晓宁

(华电郑州机械设计研究院有限公司， 郑州 450046)

0 引言

主汽温作为超超临界机组的一个重要参数，为了提高其控制水平，首要工作是了解其热工特性并建立适用于控制策略研究的模型。主汽温系统具有多变量、强耦合、大惯性、大迟延等特点，且现场往往不允许进行扰动试验，使传统建模方法已经不能满足要求。而分散控制系统(DCS)、监控信息系统(SIS)等的使用，使大量现场数据可以被方便地保存和查看，其中蕴含的大量信息可以被挖掘，同时，机组仿真技术已经能够较好地模拟现场运行特性，为主汽温系统的建模提供了条件。

主元分析法(PCA)是多元统计分析的一种重要方法，可以通过对大量过程数据进行多元统计分析，找出影响所监视参数变化的主要原因，达到降维的目的。将主元分析法应用于主汽温对象的建模过程中，可以从影响主汽温的诸多因素中提取出主要影响因素，用于系统建模。

采集某1 GW超超临界机组的现场运行数据，结合主汽温的运行机理，利用主元分析法，找出影响主汽温变化的5个主要因素，将其作为输入，建立主汽温的多变量模型。

1 基于主元分析的主汽温系统变量选择

PCA是一种掌握事物主要矛盾的统计分析方法，可以有效地对多个相关的变量进行处理，将其转化为少数几个相互独立的变量，分析出多元事物中的主要影响因素，剔除噪声和冗余，将原有的复杂数据进行降维。

假设X是一个n×m的数据矩阵，其中n为样本个数，m为变量个数，矩阵X可以分解为m个向量的外积之和[1]，即：

式中：ti∈Rn为得分向量；pi∈Rm为负荷向量(i=1,2,…,m)，X的得分向量也叫做X的主元[2]。

将矩阵X进行主元分解后写为

实际应用中k往往远小于m，E为主要由测量噪声引起的误差矩阵，将E忽略掉不会引起数据中有用信息的明显损失，则X可以近似表示为：

式中：ti为Tk矩阵中的第i行；Tk由构成主元模型的k个得分向量组成；λ是前k个主元对应的特征值λi(i=1,2,…,k)组成的k×k的对角矩阵。Pk为前k个主元负荷向量。T2统计量在第i时刻的值是由多个变量共同累加所得的一个标量，可以通过单变量控制图的形式对多变量工况进行监控[3]。

根据机组运行机理，初步确定对主汽温影响较大的11个因素[4]：主汽压力、高调门开度、主蒸汽流量、二级减温喷水量、一级减温喷水量、中间点温度、给水量、燃料量、给水温度、烟气含氧量、总风量。取这11个变量的现场运行数据组成样本矩阵X，对X进行主元分析，并通过计算每个时刻T2统计量的值，绘制出各个变量对T2统计量的贡献图，根据贡献图判断主汽温变化的主导因素。

对运行数据按上述过程进行处理后，得到的相关统计信息见表1。

表1 各主元相关统计信息

主元分析结果为：11个影响主汽温的过程变量，被压缩为3个主元，其可以解释所有数据86.9%以上的变化过程，满足主元分析中要求前k(k≤m)个主元的贡献率之和达到80%以上的要求。各主元的贡献率和其累加贡献率如图1所示。

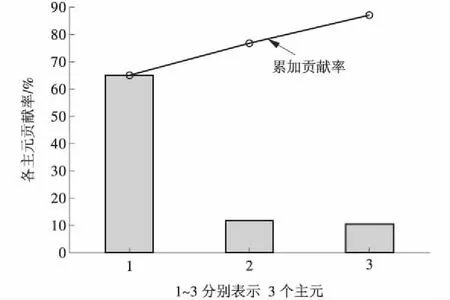
图1 各主元贡献率及其累加贡献率

对主汽温系统数据进行T2统计量的分析，T2统计量和主汽温变化曲线如图2所示，可以看出，主汽温波动较大的时刻和T2统计量较大的时刻相对应，在该采样时刻，各过程变量对第一主元的贡献得分如图3所示，可以看出，在T2统计量较大的时刻，变量3，4，7，8，10对 统计量的贡献较大，变量3，4，7，8，10分别为主蒸汽流量、二级减温喷水量、给水量、燃料量、烟气含氧量。

图2 统计量和主汽温变化过程曲线

图3 对应于T2统计量较大时刻第一主元贡献得分

由于第一主元可以解释全部数据的64.8%以上的变化过程，并且在 统计量较大的时刻，变量主蒸汽流量、二级减温喷水量、给水量、燃料量、烟气含氧量对第一主元的贡献较大，因此可以认为此时这5个变量对主汽温影响较大。

根据超超临界机组实际运行情况，燃料量和给水量直接影响主汽温，对主汽温起粗调作用，主蒸汽流量的大小直接影响烟气侧和蒸汽侧的传热，对主汽温影响较大，二级减温喷水量对主汽温起细调作用，烟气含氧量的高低直接反映风量和燃料量的配比是否合适，是反映炉膛燃烧效果的重要参数，而炉膛燃烧效果影响烟气侧和蒸汽侧传热，从而较大程度上影响主汽温。主元分析的结果和实际相符，可以将此5个因素作为主汽温系统输入变量。

2 主汽温系统的多变量辨识

主汽温系统存在多个变量，传统模型建立方法中的一种是测试建模法，其中常用的就是阶跃响应法，但在实际电力生产过程中的应用有严格的条件限制，过大的扰动会使正常生产过程受到严重的干扰，甚至造成重大事故，因此，一般的理论研究不能随意在实际系统中作扰动试验。另一种方法是将多入单出(MISO)系统视为多个单入单出(SISO)系统的叠加形式，这对于闭环运行系统的辨识带来的一定的问题，即在系统正常的运行数据中很难保证可以找到足够长时间的数据段，满足在这段数据中只有一个变量变化而其他量保持不变。本文以机理建模法建立的仿真机为平台，在此电厂1×103MW超超临界机组机理模型上进行阶跃试验，得到主汽温系统在各变量单独扰动下的飞升曲线，确定主汽温系统各传递函数的模型结构和各参数的取值，作为基准参数。

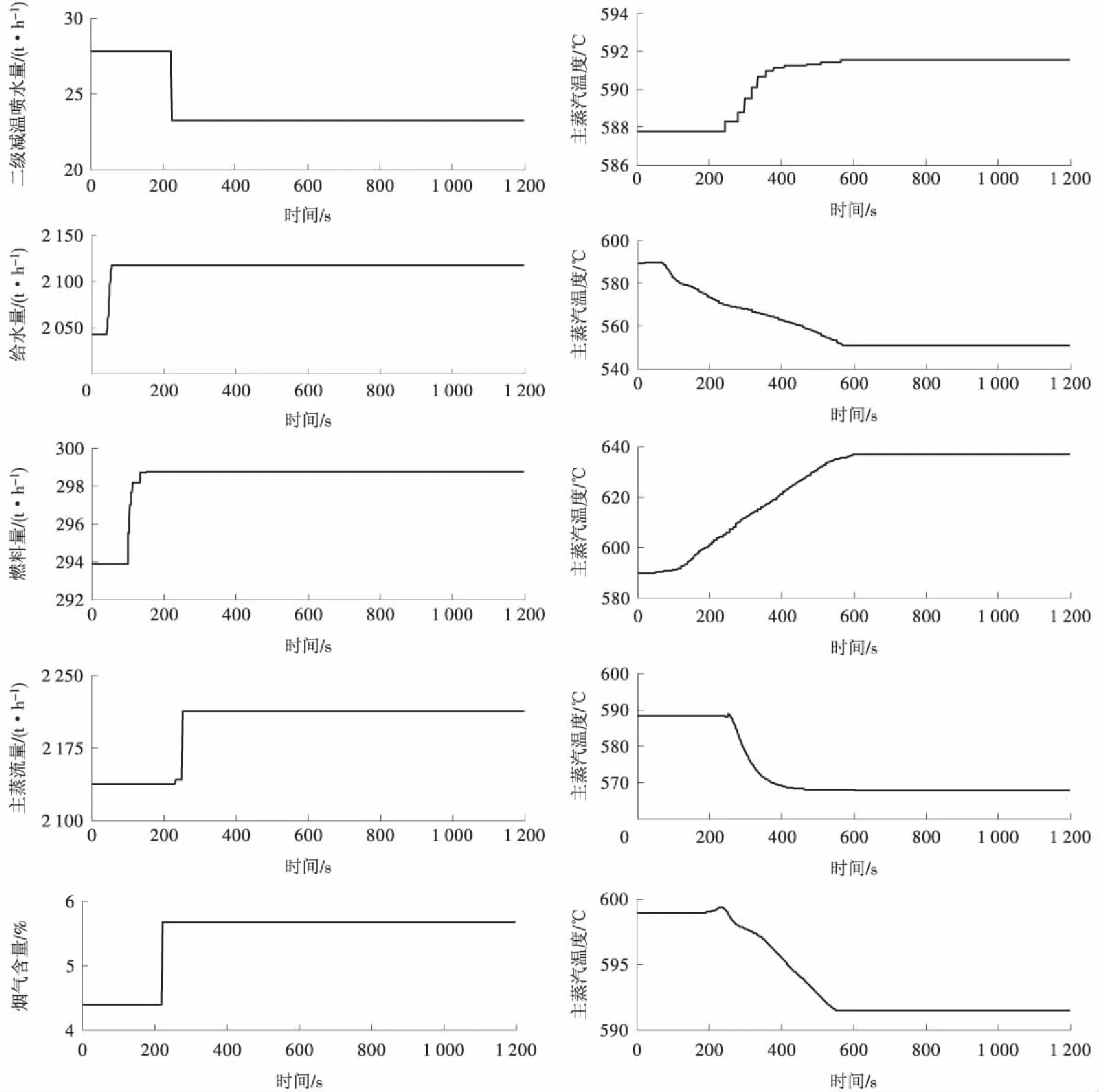
图4 各主要变量单独扰动下主汽温阶跃响应

试验过程对象均是有自平衡能力的，同时，通过专家经验判断，模型可以控制在三阶以内[5-7]，根据模型结构部分的分析，纯迟延环节和惯性环节之间可以进行转换。本文选取的传递函数采用形式为

适应度函数采用均方差标准，即

其中，K为增益系数，T1、T2为惯性时间常数，N为采样数据个数。

2.1 单位阶跃扰动下的建模

利用仿真系统，取机组75%负荷稳定运行工况，分别对影响主汽温的5个主要因素进行阶跃扰动试验，结果如图4所示。

利用PSO算法进行辨识，结果见表2。

表2 各阶跃响应辨识结果

图6 现场运行历史数据

2.2 主汽温系统多变量建模

综合前面分析，建立主汽温系统的多变量模型，输入量有5个，输出量为主汽温，结构如图5。

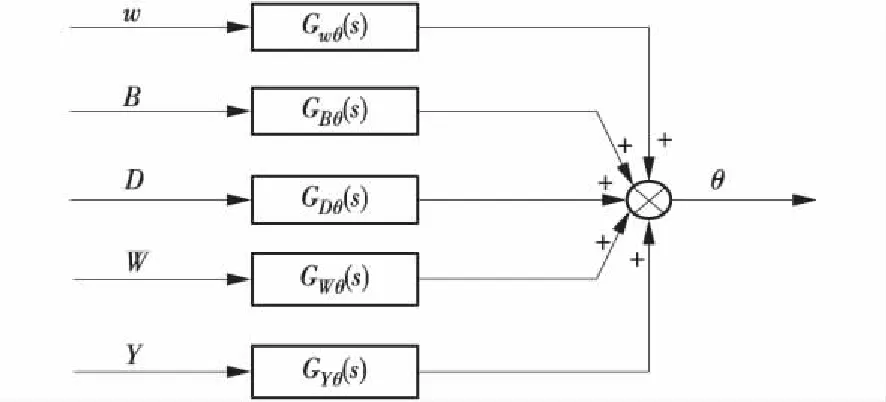
图5 主汽温多变量模型系统结构

图中，w为二级减温喷水量，B为燃料量，D为主蒸汽流量，W为给水量，Y为烟气含氧量，θ为主汽温，Gwθ(s)、GBθ(s)、GDθ(s)、GWθ(s)、GYθ(s)分别为各通道传递函数。

尽管仿真系统建模过程中存在不可避免的简化过程，导致输出模型数据和现场实际运行数据之间存在不可消除的误差，但可以在最大程度上模拟机组的静态特性和动态特性，因此，可以利用现场实际运行数据，以阶跃模型参数为基准，进行上下参数寻优，得到真正适合实际运行的多变量模型。

采集现场正常工况连续运行的历史数据，采样时间为10 s,选取其中75%负荷工况稳定运行数据，如图6所示，所选数据起于稳定点，止于稳定点。

本文采用以下方案对现场数据进行辨识：即以仿真机数据建立的模型参数为基础，在对多变量系统各通道传递函数参数进行同时辨识时，其寻优邻域值分别在表2的参数周围进行上下50%的浮动，作为现场数据辨识的初始值，对各参数进行寻优，若某个变量辨识结果处于寻优边界值，则单独对其进行寻优邻域的边界值进行50%的扩大，经30次尝试和修正，选取辨识效果最好的结果作为最终模型函数。用此方案，75%负荷下辨识结果如图7所示。

图7 本文方案的零初始值主汽温系统辨识结果

同时，为了对比上述方法和直接辨识法的优劣，采用同样的数据，只是根据理论知识，将各邻域选择为T1∈(0,5 000)，T2∈(0,2 000)，K值的选择根据对象特性定为(-20，0)或(0，20)，则通过30次训练后选取最好结果，如图8所示。对比图7和图8，前者均方差为0.677，后者均方差为1.56，显然前者的辨识效果要好于后者，证明本文所采取的多变量辨识方法是有效的。

图8 直接辨识法的零初始值主汽温系统辨识结果

采用本文方案得到75%负荷工况下，主汽温系统多变量模型各通道传递函数见表3。

2.3 模型的验证

上面辨识得到的模型基本可以反映主汽温系统输入和输出的关系，但是不能证明所得模型可以完全代表相同工况点的主汽温系统热工特性，因此，需要再用辨识数据时间段之外的数据进行模型的验证。本文选取一天后同样负荷工况稳定运行的数据，进行模型验证，验证所用现场运行数据如图9所示，同样，利用现场数据进行验证前，对数据进行滤波处理和零初始值处理，验证结果如图10所示。

从验证结果可以看出，本文所辨识的主汽温系统的模型的输出值与现场实际运行数据大体一致，所得模型可以用来进行主汽温系统控制的研究。

表3 多变量模型辨识结果

图9 主汽温系统模型验证现场数据

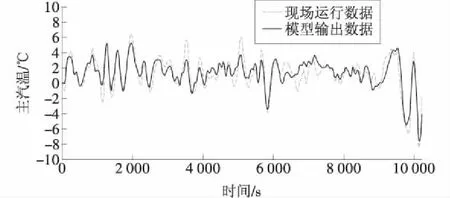
图10 零初始值主汽温系统模型验证结果

同样的，采用本文方法对90%负荷运行工况进行辨识，效果较好，证明本文方法的有效性。

3 结论

本文将机理建模、试验建模和智能优化建模相结合，建立了主汽温系统的多变量模型。以仿真系统中阶跃扰动试验建立的SISO系统模型参数为基础，通过从大量的现场运行数据中遴选出适用于建模的数据，利用粒子群智能寻优算法，以SISO模型参数为基准，进行上下寻优，对仿真系统模型进行进一步校正，得到适用于现场数据的主汽温多变量系统MISO模型，并通过验证，证明所建立出的模型可以用于主汽温系统控制的研究。