倾斜板表面微结构上液膜流动影响因素分析

杨 立 蒋 斌

（西南科技大学 绵阳 621010）

0 引言

液膜流动广泛的存在于自然环境中。平板上液膜流动是液体和气体或另一种不相溶的液体在平整或表面有微结构的板面上流动。液膜流动里包含着丰富的流体力学知识，这种流动形式具有优良的传热传质效果，广泛应用于填料塔、火箭发动机燃烧室冷却[1]、液膜蒸发器[2]和核电站安全壳液膜蒸发冷却方案[3]等。不少学者都对液膜流动进行了研究分析。李春曦[4]利用PDECOL程序研究了壁面微结构对超薄液膜流动的影响，研究发现不平整的微尺度基底引起液体局部压力的变化，各种壁面结构对液体表面变形有增强作用；谷芳[5]对倾斜波纹板上液膜流动进行了二维模拟分析发现小的接触角可以更好的润湿壁面；刘梅[6]对二维非平整倾斜表面上流动液膜的影响因素进行了分析指出表面张力、流体物性和入口速度均对液膜的流动有影响；吴正人[7]对不同尺度的三角形结构上液膜流动特性进行了数值模拟，结果表明液膜自由液面随三角形结构呈规律变化，当结构宽度足够大时，液面位置变化不再明显；蒋斌[8]分析了壁面接触角和表面张力对液膜表面的影响，发现表面张力的变化明显的引起了液膜边界发生波动。卢川[9]等人通过实验探究了下降液膜的不稳定性，指出重力对扰动波波长影响显著，惯性力对于扰动波的出现和维持有重要影响。本文通过数值计算，探究了倾斜版表面微结构上液膜流动的影响因素。

1 数学物理模型

1.1 物理模型

图1 物理模型Fig.1 Physical model

采取四边形结构化网格对模型进行网格划分，在液相入口1mm的高度上调整了不同的划分方案，分别得到8750、9500、10250、11250共4种不同数目的网格，并以此作网格无关性验证。结果表明：随着网格数目的增长，液膜厚度逐渐降低，当网格数目为10250时，液膜厚度与网格数目为11250时几乎一致，充分考虑计算精度和迭代时间，选择网格数为10250的划分方案，即在液相入口1mm的高度上使用大小为0.0625mm的网格进行网格加密。

1.2 数学模型

作如下假设：

（1）流体为连续不可压缩牛顿流体，层流流动；

（2）流体物性参数恒定为常数。

1.2.1 体积分数方程

在VOF模型中，各相流体共享一个方程组，每一相的体积分数在整个计算区域内被追踪，该方法能准确的计算存在自由液面的多相流动，其控制方程为：

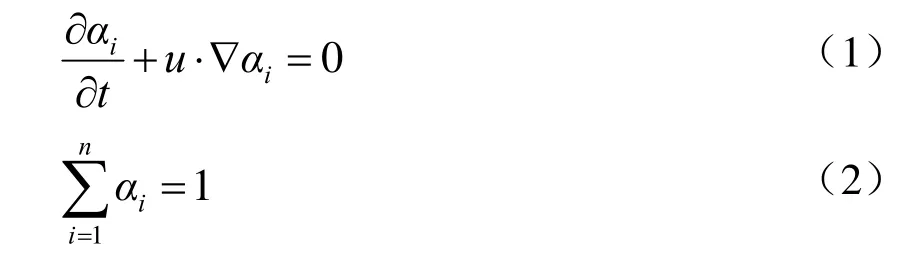
式中：ai为第i相的体积分数；u为第i相的速度，m/s。

本文只包含气液两相，取n=2，控制方程中的密度粘度由每个相共同决定，因此，气液两相系统中密度ρ和粘度μ表示为：

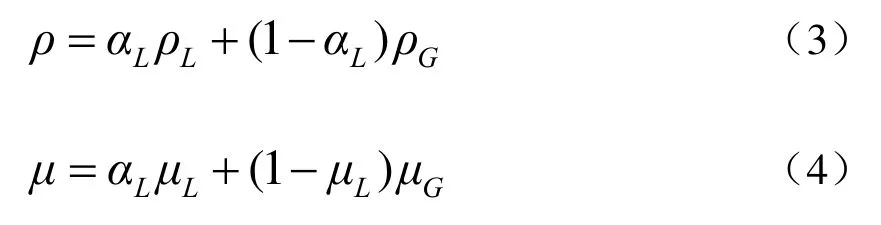
1.2.2 质量守恒方程

式中，ρ由式（3）计算得到。

1.2.3 动量方程

在整个区域内求解单一动量方程，所得到的速度场被所有相共用。动量方程通过物性参数ρ和u与体积分数相联系：

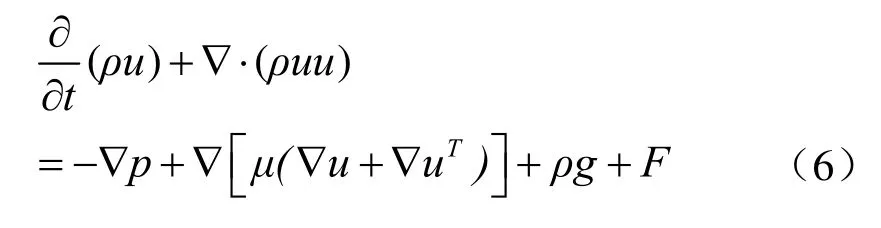
在存在自由液面的流动过程中，表面张力对流动的影响非常重要，不可忽略。本文采用Brackbill[10]提出的CSF模型计算表面张力源项，在动量方程中表面张力源项为：

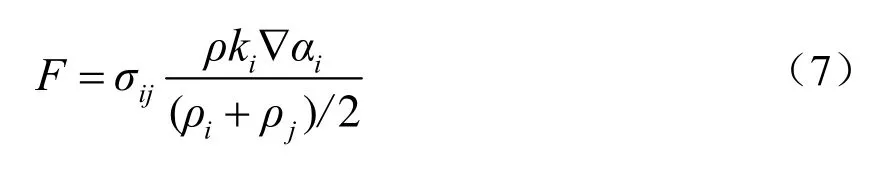
式中，σij为气液界面张力系数，N/m；k为界面曲率，由界面处单位法向量n⇀表示。

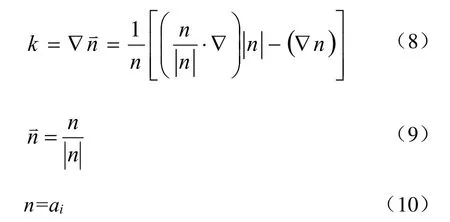
1.2.4 雷诺数定义

式中，δ为液膜厚度，m；υ为流体运动粘度，m2/s。

1.3 计算方法与边界条件

采用VOF模型，液体区域对边界层网格加密处理，压力项采用PRESTO！算法；压力-速度耦合方程的求解采用PISO（pressure implicit with splitting of operators）方法；动量项采用二阶迎风格式；体积分数项采用Geo-Reconstruct格式；时间步长取10-5；平板倾斜角度为45°。

液相入口为速度入口，出口为压力出口；气相进出口为压力进口和压力出口。对称边界条件除了可以描述有对称轴的物理模型外，还可以描述粘性流体中剪应力为零的滑脱壁面条件[11]，因此在气相界面不受任何力的作用，将气相侧（Top）视为壁面无滑脱条件，用Symmetry边界来描述。计算物性参数如表1所示。

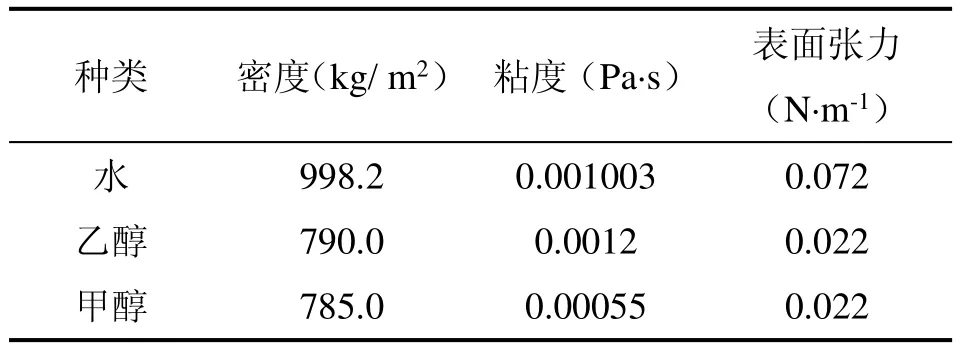
表1 流体物性参数Table 1 Physical properties of liquid

不同的微结构平板参数如表2所示。

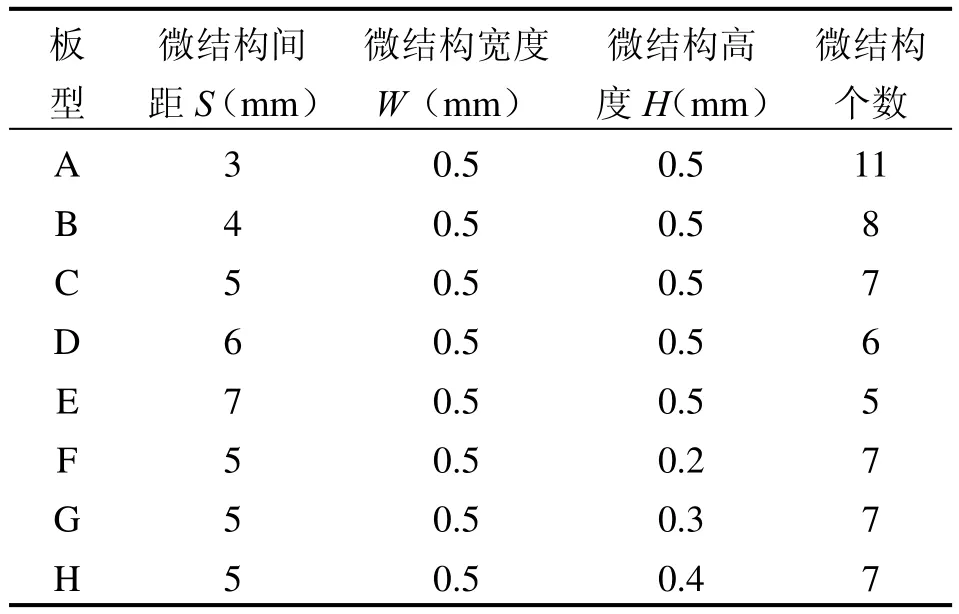
表2 微结构计算参数Table 2 Calculation parameters of Microstructure

1.4 分析段的选择

以体积分数为0.5作为气液相的交界面，即流体的自由液面。以版型C、介质水为例，图2是版型C上自由液面不同波段的划分和对比。将自由液面划分成9个部分，其中选取7个波段（每个5.5mm）并且将每个波段的形状进行比较。

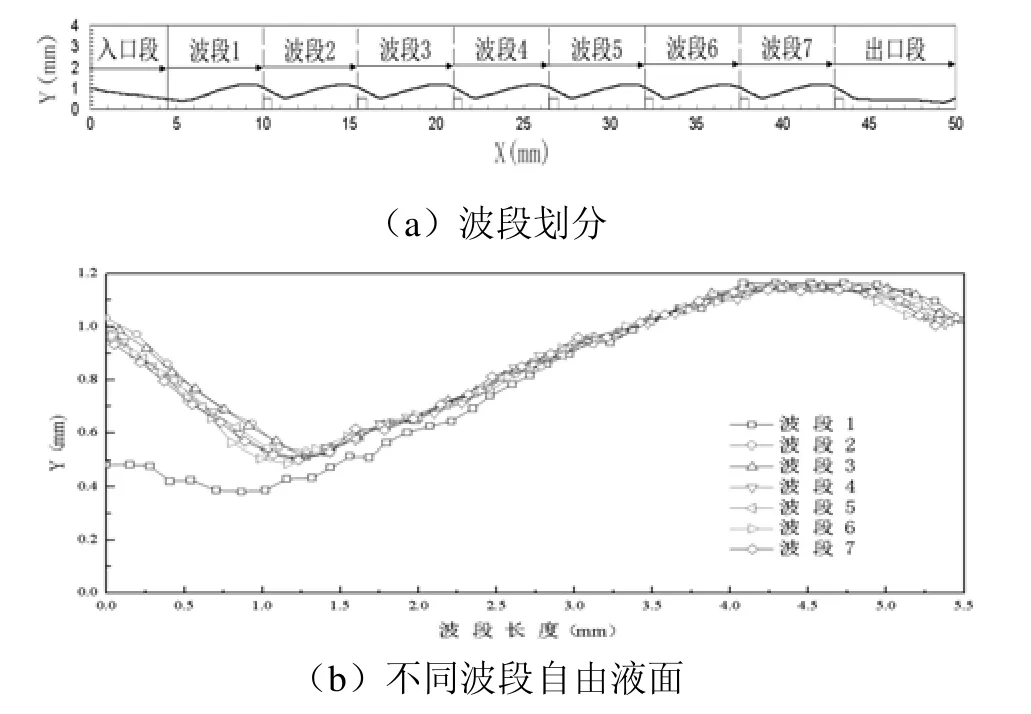
图2 不同波段的比较Fig.2 Comparison of different waves

由图2可以看出，波段2、3、4、5、6、7的形状相吻合，而波段1与其他部分波形不相同，不能用于分析；同时，从图4波段划分中也能看出入口段和出口段波形与微结构上的波形完全不同，故在以后的分析过程中，均不包含入口段，出口段以及波段1。

图3 不同接触角自由液面Fig.3 Free surface of liquid film with different contact angles

图3是不同接触角下，介质水流过版型C液膜的自由液面，从图中可以看出接触角10°至30°的范围内，波形几乎完全相同。研究还发现，随着接触角的增加，液膜自由液面波动增强，特别是当接触角不断增大时，液膜发生破断。为了在研究中液膜表面稳定且在分析段内有相同的波形，故在研究中均设置接触角为20°。

2 结果与分析

2.1 微结构参数的影响

2.1.1 微结构高度的影响

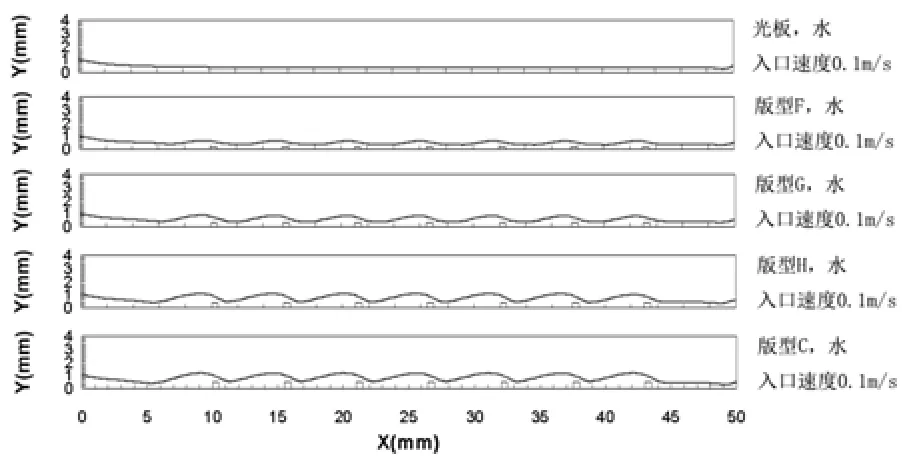
图4 不同高度的微结构上液膜自由液面Fig.4 Free surface of liquid film on the microstructure with different height

通过版型F、版型G、版型H和版型E在相同入口速度和物性参数条件下，研究了微结构高度对液膜流动的影响，从图4中可以看出没有微结构的光板上液膜流动是平坦的；当表面存在微结构时，液膜表面波动增强，呈现波浪状，且微结构高度越高，波浪幅度越大；液膜的波峰出现在微结构上游，并在下游处形成较薄的液膜。模拟结果和文献[12]中所描述的现象一致，也说明了本文数值方法的可行性。

2.1.2 微结构间距的影响

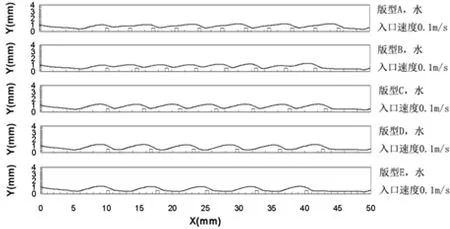
图5 不同间距的微结构上液膜自由液面Fig.5 Free surface of liquid film on the microstructure with different spacing

图5展示了不同间距（S=3,4,5,6,7mm）的微结构上液膜状态。可以看出液膜表面的波动程度随着间距的增大愈加明显，当间距S=3mm时，液膜并没有像其他间距那样在每一个微结构上下游出现波峰和波谷，而是相邻的两个微结构共享一个波峰和波谷，这可能是由于间距过小，不足以使流体在相邻两个微结构之间形成薄液膜。

2.2 流体物性的影响

2.2.1 流体粘度的影响

选用甲醇和乙醇作为研究介质，从表1可以看出，这两种流体表面张力相同，密度相差很小，但粘度相差较大。

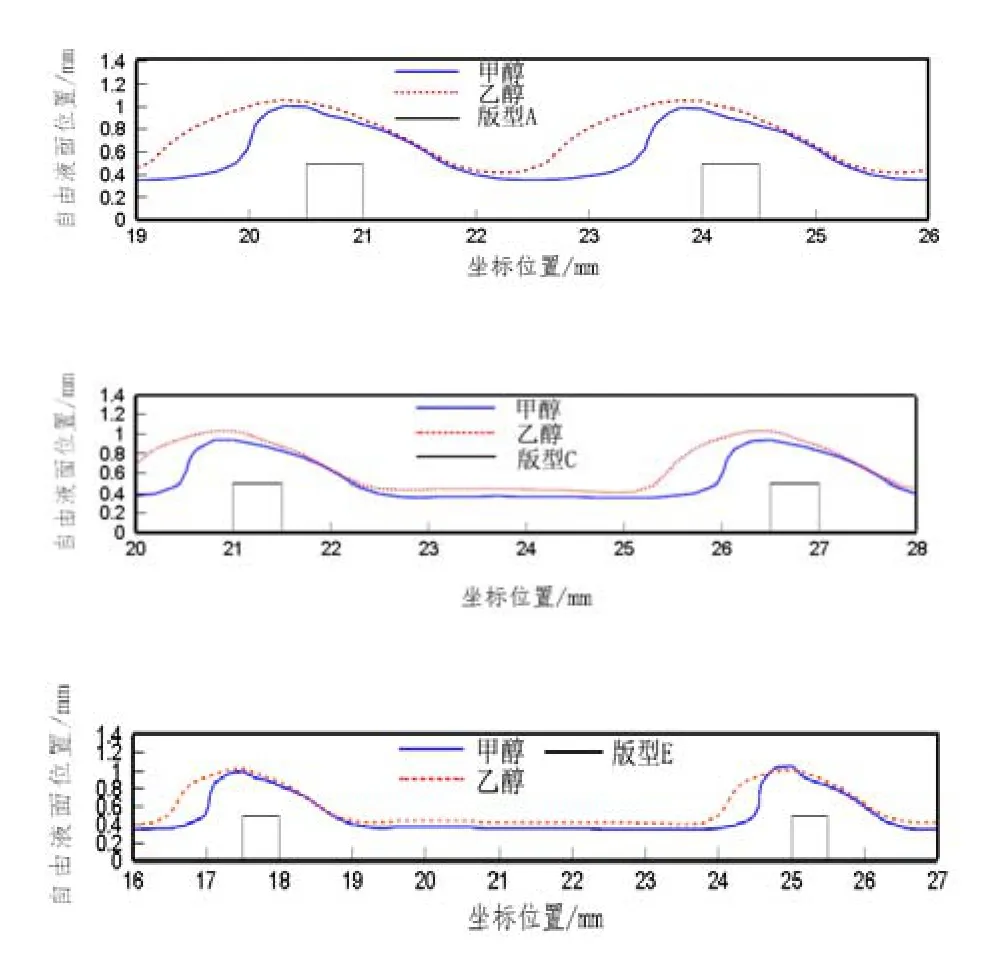
图6 不同粘度的流体自由液面位置Fig.6 Free surface of liquid film with different viscosity

图6为同一入口速度（0.1m/s），三种间距（S=3,5,7,mm）条件下，甲醇和乙醇的自由液面位置，从图中可以看出粘度较大的乙醇液膜比甲醇液膜更厚，且相对甲醇，乙醇液膜在微结构处形成的波浪形状更加平滑，粘度小的甲醇只在贴近微结构壁面附近凸起波动；同时从图中可以看出，相同入口条件下，两者液膜波峰出现的位置和微结构的相位差几乎相同，即减少流体粘度可以减少液膜厚度，但不影响其液面与微结构的相位差。

2.2.2 表面张力的影响

以版型C，流体介质为水，入口速度（0.1m/s）为例，探究了表面张力对液膜流动的影响。三种不同表面张力系数的液膜自由液面位置如图7所示。可以看出表面张力影响液膜的厚度，液膜厚度随着表面张力的增大而增大；从图中还可以看出液膜波峰微结构位置的相位差与表面张力有关，表面张力增大，相位差增大，液膜波峰出现在微结构偏上游位置。

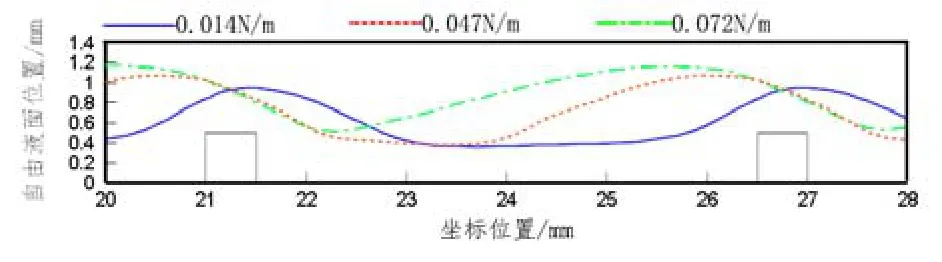
图7 不同表面张力系数液膜自由液面Fig.7 Free surface of liquid film with different surface tension

2.2.3 速度的影响

图8中流体介质为水，以版型C为例，探究了速度对液膜流动的影响。显然不同速度下（0.05m/s～0.2m/s），流体均随着微结构的出现而产生了波浪状的周期液膜。且随着速度的增大，液膜厚度先增加后减小，这可能是因为当速度过大时，对平板表面的冲刷效果超过了粘滞力使液膜粘附在平板上的效果。从图中还可以看出随着速度的增加，液膜波峰和微结构的相位差逐渐减小。

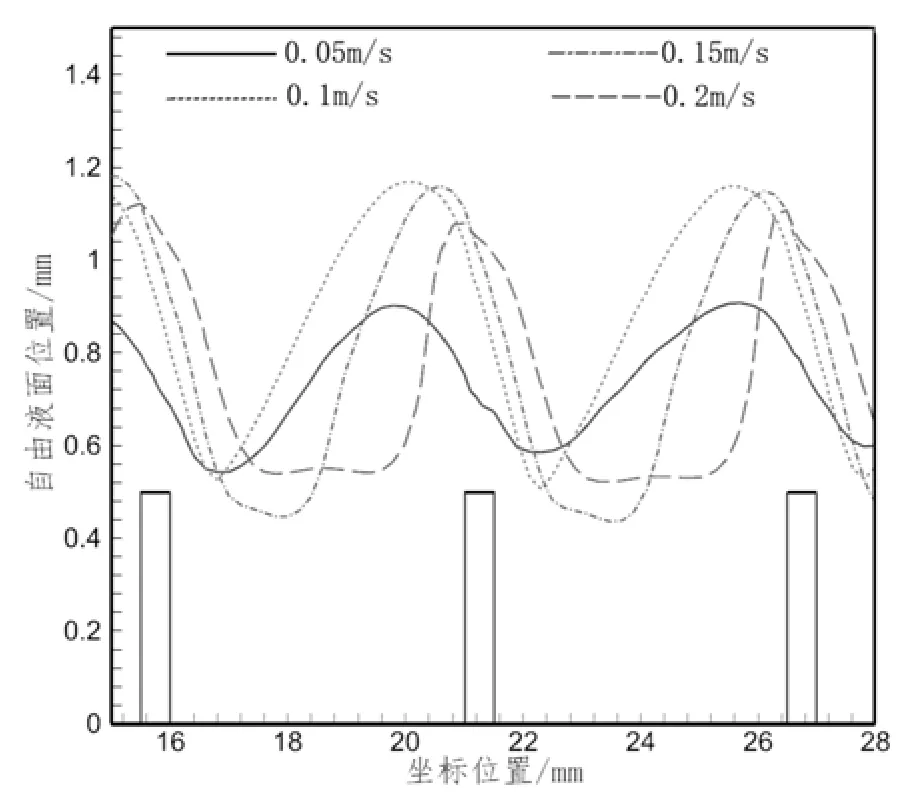
图8 不同速度液膜自由液面Fig.8 Free surface of liquid film with different speed

2.3 液膜的特征

下降液膜流过微结构时，引起液面波动产生波浪状液膜，增加了气液界面面积。界面面积的增加会增强传质的效果。以VOF体积分数0.5作为气液两相交界面，研究不同物性，不同微结构参数下的液膜振幅。

图9 不同参数液膜波动的振幅Fig.9 The amplitude of the fluctuation of the liquid film with different parameters

图9是相同入口速度（0.1mm）条件、不同微结构间距、不同物性参数下的液膜振幅，从图中可以看出在间距大小大于4mm时，液膜振幅出现规律性变化，随着微结构之间间距的增大，液膜振幅开始随之增大，随后趋于稳定。同时可以看出密度和表面张力相接近的甲醇和乙醇，在液膜振幅上出现统一规律，且乙醇液膜振幅大于甲醇液膜。另外，从图中可以看出当流体为水，微结构间距为3mm时，出现不符合规律的数据点，这是因为，如同2.1.2节中的分析，在介质为水时，由于微结构间距过小，此时液膜并没有在每一个微结构附近形成波动液膜，而是两个微结构共享一个波峰和波谷，此时液膜振幅不符合上述分析规律。

3 结论

通过有效的数值模拟，探究了表面有微结构存在的倾斜板上液膜流动问题，分析了不同参数对液膜流动的影响。研究结果表明。

（1）微结构的高度影响液膜表面的波动程度，更高的高度带来波动更大的液膜；微结构的间距增大，会使得液膜波动程度先增加后稳定不变。

（2）流体的粘度会影响液膜的厚度，但不会影响液膜波峰与微结构位置的相位差；而表面张力既改变液膜厚度也改变波峰与微结构位置的相位差，随着表面张力的增大，液膜厚度和相位差均增大；液体速度影响液膜厚度和相位差，速度越大，相位差越小。

（3）液膜的振幅由微结构间距和流体物性共同决定，但都表现出规律性，当微结构间距增大时，液膜振幅先增大后稳定不变。