从“小孩拉船”问题谈起

张万军

(乌鲁木齐市教育研究中心,新疆 乌鲁木齐 830002)

1 问题

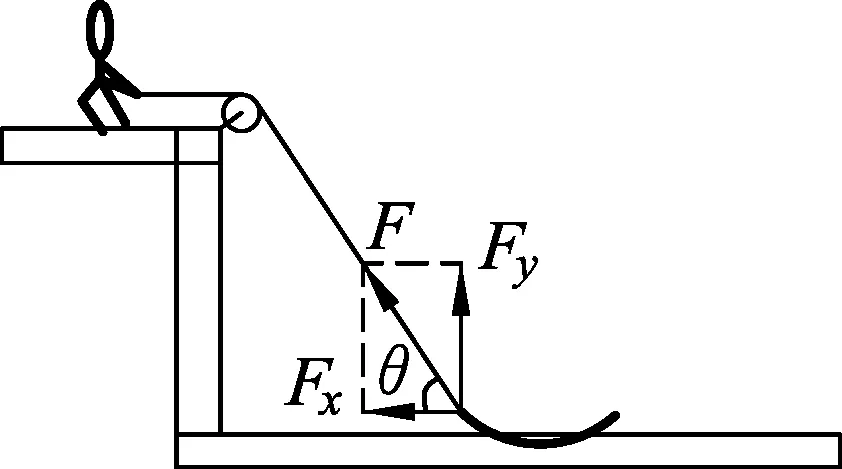
图1

如图1,小孩在岸上用绳子匀速拉船,船做什么运动?船的速度大还是小孩的速度大?

常见错误:小孩匀速运动,船当然就匀速运动了．船的速度是小孩的速度的一个分速度,即v船=v人cosθ，所以船的速度小于小孩的速度．

2 分析

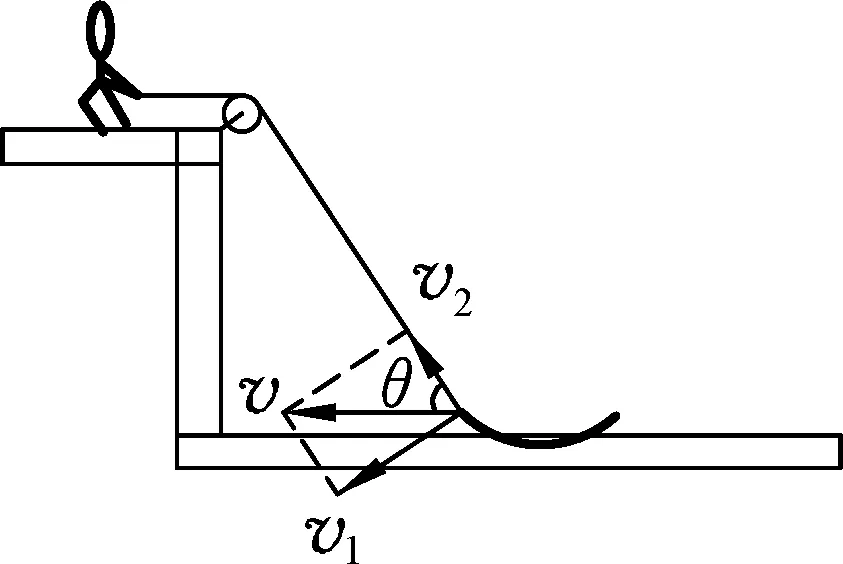
图2

事实上,如图2,一方面船随着绳子的收缩靠近岸边,另一方面,船绕着滑轮旋转．即船参与了两个运动:绕着滑轮转动的运动,线速度是v1;沿着绳子的运动,速度是v2．船的速度v实际上是v1、v2的矢量和,不是绳子速度的一个分速度．

从力的角度也可以说明船的运动是合运动不是分运动．物体运动的变化取决于其受到的合外力,船受到的力包括重力、拉力、阻力、浮力,这4个力合力在水平方向,而船实际运动的方向也在这个方向上．从牛顿第二定律可知,在直线上运动的物体,合力也在这条直线上,而合力当然对应着合运动．

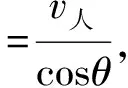
3 速度大小关系的实验验证

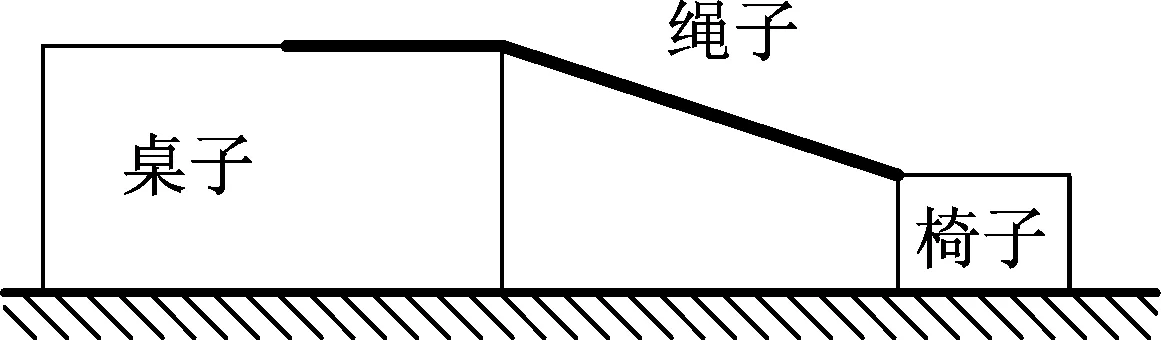
图3

上述问题也可借助于简易实验来进行验证.如图3,用绳子拉动椅子一段距离,用刻度尺量出绳头移动的距离x1,椅子移动的距离x2,可得到x2>x1,即椅子的速度大于桌子的速度．该实验简单易行，可定性地说明船的速度大于小孩速度.

4 定量分析

如图4,让船运动一段距离Δx,相应地绳子缩短了Δs,即t时刻人运动的距离有

x2=H2+s2，

t+Δt时刻有(x-Δx)2=H2+(s-Δs)2，

两式相减得

2xΔx+Δx2=2sΔs+Δs2.

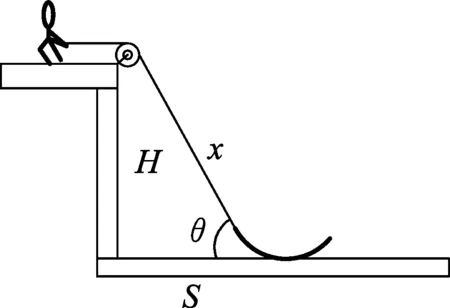
图4

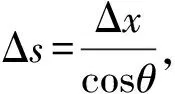
图5

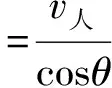
5 类似的问题

“小孩拉船”问题是一个应用很广泛的模型．许多问题都“相当于”这个问题,最后都可以“化归”为这个模型．请看下面几例．

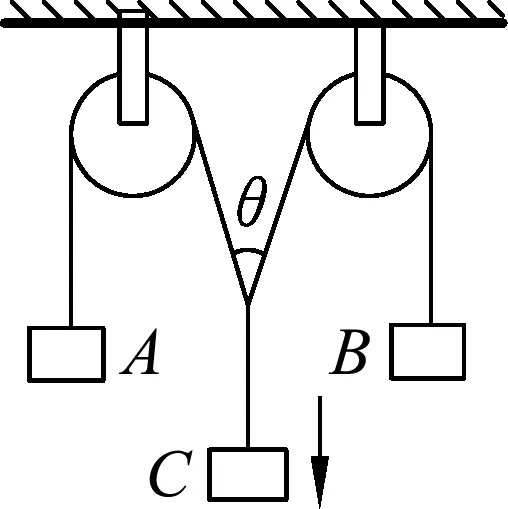
图6

例1.如图6,有3个相同的物块,如图6所示连接,释放C后,确定3个物块的速度关系．

这个问题本质上就是小孩拉船模型．A(或B)相当于小孩,C相当于小船．所以有

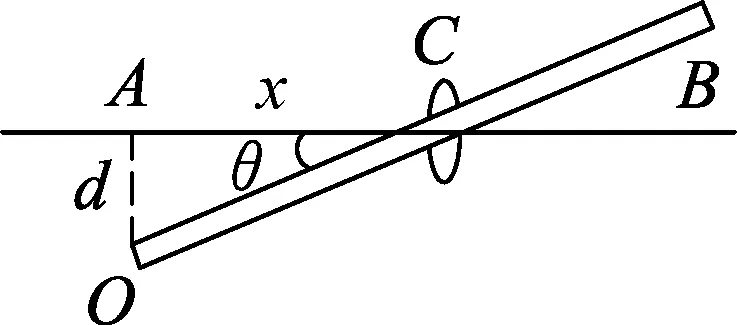
图7

例2.如图7,细杆绕固定点O点以角速度ω匀角速度转动,并推动小环C在固定的钢丝AB上滑动．当小环距A的距离为x时,小环的速度多大？(d是已知量)

小环C相当于小船,C与杆的接触点沿着杆的速度相当于小孩的速度．所以

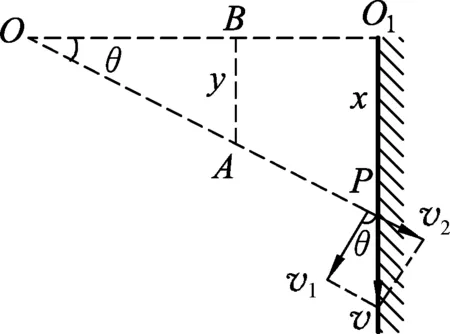
图8

例3.如图8,从距竖直墙壁为L的O点水平抛出一个初速度为v0的小球．O点还有一个可以转动的点光源,随时跟踪照射小球,小球会在竖直墙壁上留下影子,判断影子做什么运动．

刚抛出小球时,影子在O1,当小球在任意位置A点时,影子在墙上的P点．这个问题也可以看做小孩拉小船问题．

影子相当于小船,其速度v是v2(相当于小孩速度)和v1(绕O点转动的速度)的矢量合．

下面求一下点光源以怎样的角速度ω转动才能跟踪上小球．

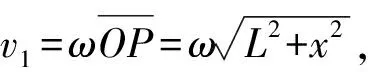
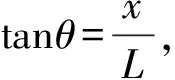
6 结束语

“小孩拉船问题”虽然古老,但不同时期的学生都会由此暴露出相同的问题,这些问题是很好的教学资源．只要用得好,会进一步加深学生对物理学习的兴趣以及对物理原理的理解,可以使“科学思维”这一物理学科核心素养通过具体问题的分析和“化归”落地．从这个角度来看,“小孩拉船问题”的价值可谓历久弥新．很多问题,表面上看起来“新鲜”,但本质上和“小孩拉船问题”如出一辙,只要我们善于观察和分析,就能将看似“新鲜”的问题“化归”为已知的熟悉的问题．在表面上不同的事物之间寻找它们的联系是物理学永远追求的主题．