基于权值变化的BP神经网络自适应学习率改进研究①

朱振国, 田松禄

(重庆交通大学 信息科学与工程学院, 重庆 400074)

引言

BP神经网络(Back-Propagation Neural Network),是由Rumelhart和McCelland等科学家提出, 利用输入信号前向传播、误差反馈信号反向传播和梯度下降的原理, 并通过链式求导法则, 获取权值更新变化大小的依据, 使权值可以按照一定的大小进行更新, 达到减小误差、得到理想输出的一种算法. 常用于预测、回归问题的判别, 是目前应用最为广泛的神经网络之一[1].

但传统BP神经网络, 比如: 学习率为固定值, 学习率设置偏大, 容易导致学习震荡甚至发散, 而无法收敛;学习率设置偏小, 容易导致学习速率慢, 收敛过于缓慢;对于这种由于学习率人为设定不合理的问题, 不能较好地建立输入输出的非线性映射关系, 而导致BP神经网络难以推广应用[2].

针对BP神经网络学习率的人为设定不合理的问题, 本文提出基于权值变化的自适应学习率模型, 改进了传统神经网络的固定学习率设置不合理的弊端; 并将正态分布结合神经网络的误差函数, 加快收敛速度;利用梯度上升法, 以保证正态分布的合理应用.

1 神经网络

对于三层 BP神经网络, 输入X1、X2、X3…Xn, 输出为Y, 隐含层输入权值为输出层权值为为阈值, L为层数, ij表示前层第i个的和后层第j个神经元表示激活函数[3]. 隐层神经元净输入值为:

f(·)的导数为:

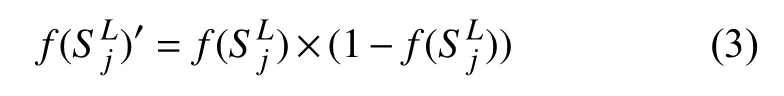
期望输出用d表示, 实际输出为Y; 误差函数err的表达式为[4]:

式(4)可以看出, 存在理想极小值点err=0, 但实际很难达到该点, 通常是根据误差反向传播与梯度下降法[5], 多次迭代更新权值, 使实际输出Y无限逼近期望输出d, 达到误差err逼近0的目的[6–9].

2 正态分布模型和自适应学习率的BP神经网络

2.1 正态分布模型

引入正态分布模型到BP神经网络中, 将误差err作为正态分布函数的自变量, 令正态分布模型的期望u为0, 正态分布函数值取得最大值, 误差err趋近于u, 如图1.

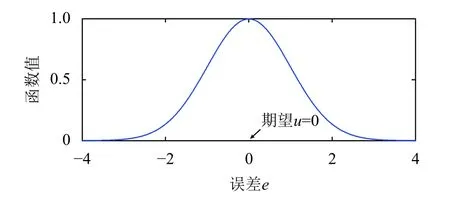
图1 正态分布函数图

当期望u=0时, 正态分布函数:

网络训练目标是取得正态分布函数最大值, 目标达成, 则网络误差为0, 权值更新达到最佳状态.

本文借鉴用于取得局部最小值的梯度下降法(要求误差函数为凹函数)思想, 反向推理, 采用梯度上升法(要求误差函数为凸函数)寻找正态分布的最大值.

以图1和式(5)为例, 解释梯度上升法能取得局部最大值的原理:

2.2 自适应学习率模型

提出基于权值变化的自适应学习率定义为:

其中t是BP神经网络的权值变化:

β(t)函数曲线图为图2.

图2 自适应学习率的曲线图

图2中n为β的倾斜参数. 由式(7)、式(8)及图2可以得出结论, 当训练接近理想时, 权值的变化t趋于极小的值, 此时学习率β也是一个极小的值, 不利于训练的进行, 于是用扩大t的值, 调整β函数对t的敏感程度.

图3 二次函数及其切线

对于现有固定学习率的神经网络, 学习率偏大, 容易产生震荡; 学习率偏小, 收敛速度慢, 网络拟合效果差, 不利于收敛; 本文提出的自适应学习率β, 根据权值变化自适应调整大小, 当权值变化大时, 此时学习率大;当网络权值变化小, 学习率小(如图2); 在即将达到目标输出时, 误差接近极小值点, 误差曲面的梯度变化小,即此时权值变化t较小, 从而学习率较小, 更有利于得到网络收敛, 对提高误差的精度, 具有显著的作用.

此外, 在每两个神经元之间, 其连接权值都有对应的学习率; 训练过程中, 每两个神经元的连接权值时刻在变化, 其对应的学习率也变化, 所以训练过程中, 产生数以万计的学习率, 以匹配权值的变化, 适应网络更新[10].

针对现有的几种典型自适应学习率, 与本文的自适应学习率作对比:

1) 自适应全参数学习率Adagrad[11–13]是使学习率参数自适应变化, 把梯度的平方根作为学习率的分母,训练前期梯度小, 则学习率大, 训练后期, 梯度叠加增大, 学习率小; 由于累加的梯度平方根和越来越大, 学习率会逐渐变小, 最终趋于无限小, 严重影响网络收敛速度.

2) 牛顿法, 用Hessian矩阵替代学习率, 并结合梯度下降法, 虽然可得最优解, 但要存储和计算Hessian矩阵, 增大计算复杂度[14,15].

3) 本文提出基于权值变化的自适应学习率, 利用参数10n调整学习率对权值变化的敏感度, 以至于不存在如Adagrad算法的学习率趋于无限小的弊端; 本文的自适应学习率, 只需把权值更新过程中权值的导数用于学习率中, 计算的复杂度远低于牛顿法[16,17].

2.3 权值更新

采用误差反向传播方式更新权值, 使误差e更快的取得极小值.

由式(3)～(式6)、式(8)得误差偏导为:

对于基于自适应学习率的网络权值更新, 依梯度下降法得权值更新为:

正态分布模型的权值偏导为:

由式(7)、式(9)、式(11)可得:

式(12)可以看出, 网络训练后期, 误差err趋于极小的值, 此时权值变化不明显, 收敛速度慢; 为提高收敛速度, 提出解决方法为:

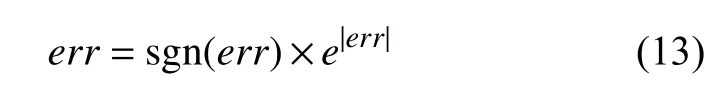
利用式(13)左边的err代替原来的误差err, 其中sgn(err)为符号函数, 定义为:

对于正态分布模型, 依梯度上升法得权值更新:

其中Wn为W更新后的权值.

对于传统模型, 依梯度下降法得权值更新为:

正态分布模型与自适应学习率结合, 依梯度上升法得权值更新为:

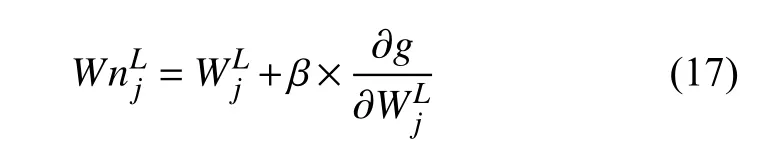
结合式(7)、式(13)、式(14)、式(17)得权值更新为:

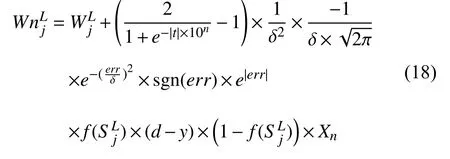
式(18)为结合梯度上升、正态分布模型、自适应学习率的权值更新方式, 与传统权值更新方式(式(16))相比, 改进后权值变化系数为:

3 实验验证

采用经典XOR问题, 验证改进BP网络; 标准XOR问题与验证XOR问题如表1.

表1 XOR问题

先用标准XOR问题对神经网络训练, 再用接近标准XOR输入对神经网络验证, 比较验证输出与标准输出, 判断优劣.

3.1 带正态分布的固定学习率模型与传统模型对比

设定学习率: 0.5, 误差限默认: 0.000 001, 迭代次数默认10 000次, 得基于正态分布模型的BP网络和传统BP网络误差曲线, 如图4.

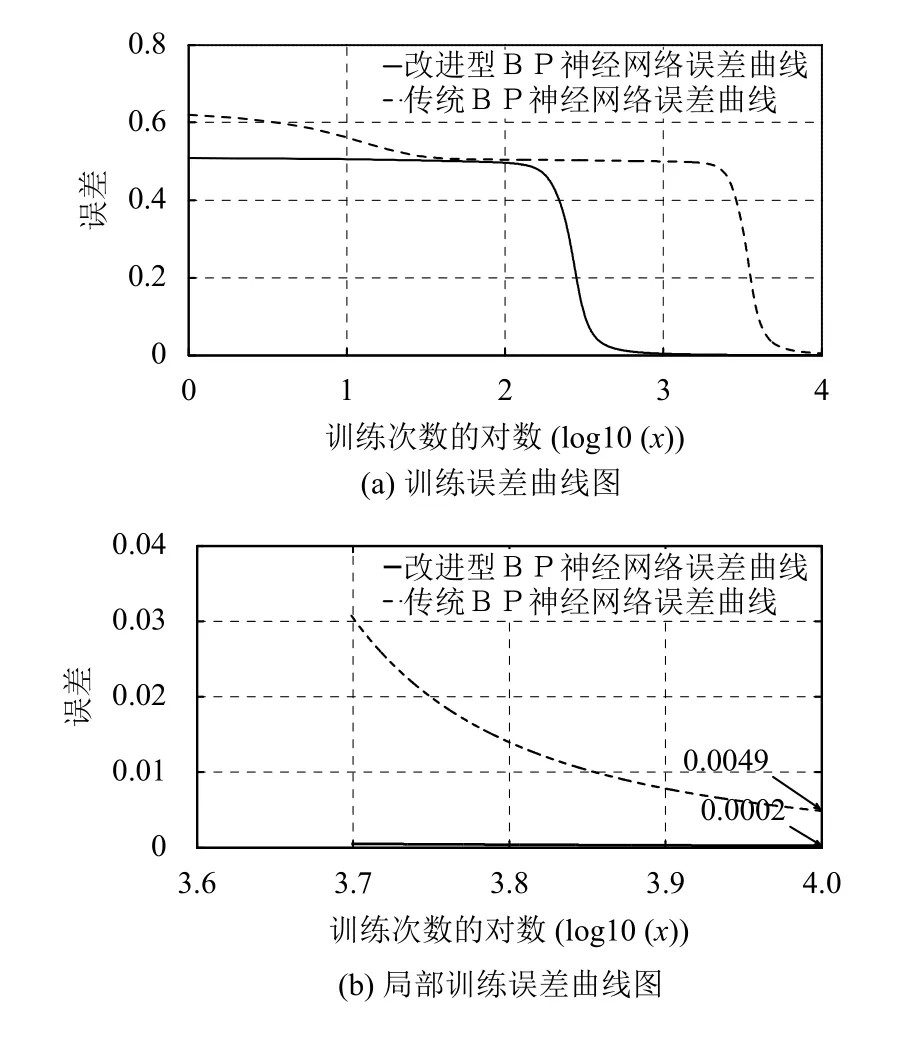
图4 正态分布模型与传统模型的误差对比

XOR异或问题的验证输出为表2.

表2 验证输出Y

从图4、表2可以看出, 基于正态分布模型改进后的网络, 其误差是传统模型的1/25, 误差明显降低, 且验证结果更接近于标准输出.

分别比较不同学习率和不同训练次数之间的误差,如表3.

从大量实验可以看出, 基于正态分布模型的BP网络与传统BP网络模型相比, 具有更小的误差或更快的迭代速度. (带*为改进模型实验误差, 带**为传统模型实验误差).

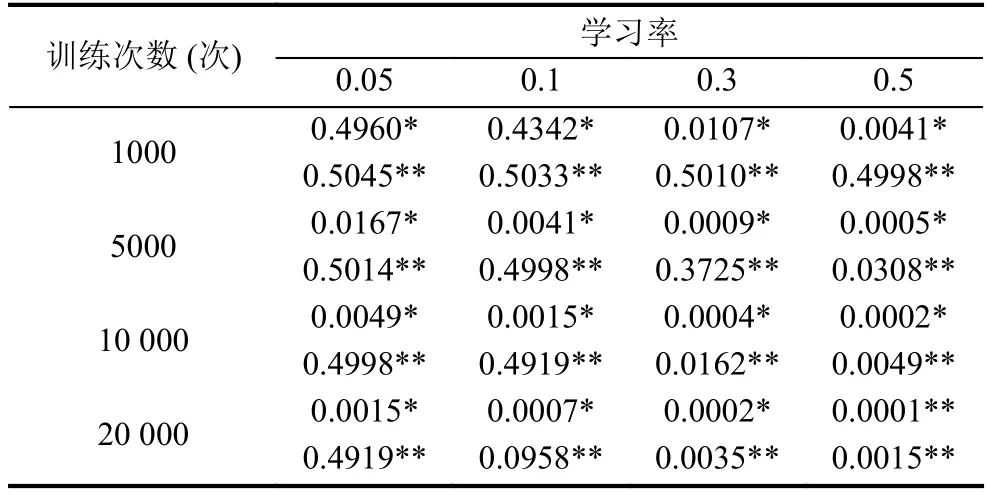
表3 不同学习率与训练次数的误差对比

3.2 自适应学率模型与固定学习率模型对比

自适应学习率的倾斜参数n设为3. 以权值变化作为自适应学习率变化依据, 采用梯度下降法更新权值.得隐含层自适应学习率变化曲线, 图5所示.

图5 自适应性学习率的变化

可以看出, 学习率是随权值的变化而自适应变化,每一轮迭代后, 权值变化不同, 导致学习率不同; 训练后期, 权值变化减小, 学习率减小, 自适应学习率相应减小.

对于固定学习率, 采用自适应学习率的算术平均值: 0.4567, 将改进型自适应学习率与固定学习率训练结果作对比, 如图6.

XOR异或问题的验证输出为表4.

可以看出, 自适应学习率模型的误差为固定学习率模型的1/2.2, 并且验证结果更接近标准XOR异或问题.

3.3 自适应学习率的正态分布模型与固定学习率模型对比

倾斜系数为3, 可得自适应性学习率的变化与训练次数之间的关系为图7.

固定学习率采用自适应学习率的算术平均值:0.1459, 与带自适应学习率和正态分布模型的BP神经网络对比, 如图8.

表4 验证输出Y

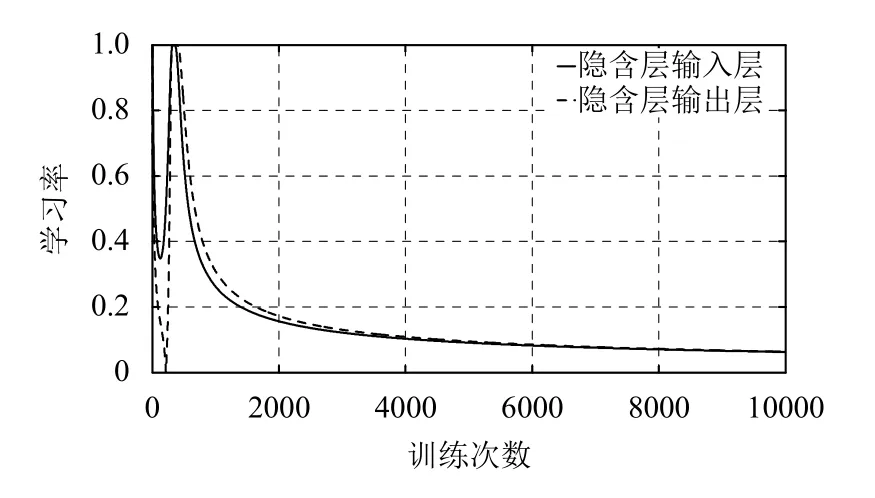
图7 自适应学习率的变化

图8 误差对比

XOR异或问题的验证输出为表5.

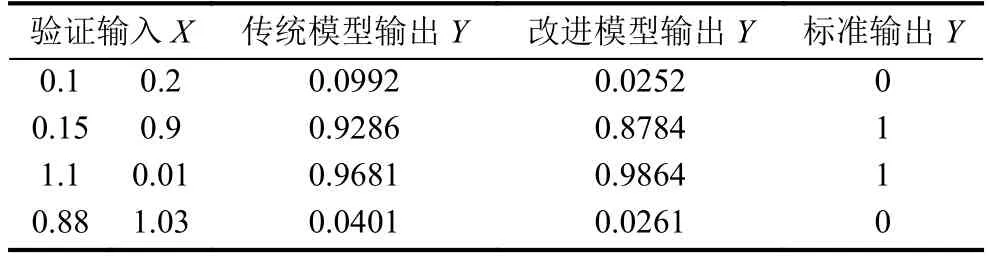
表5 验证输出Y

从图8、 表5可以看出, 改进BP神经网络的误差是传统模型的1/55, 改进的BP神经网络性能明显优于传统模型.

4 结束语

本文提出基于权值变化的自适应学习率、结合梯度上升法的正态分布模型, 提升BP神经网络的运算效率; 理论分析了提高收敛速度、降低误差的原理, 通过仿真结果表明, 改进后的BP神经网络在提高收敛速度、降低误差方面具有更好的成效.