行列式计算方法在初等数学中的应用综述
2018-07-17 02:23:32刘燕玉
数学学习与研究 2018年13期
◎刘燕玉
(铜仁学院大数据学院,贵州 铜仁 554300)
行列式是高等代数中的一个重要内容,它在许多的领域中都有非常广泛的应用,如解行星运动的微分方程组、运筹学中线性规划、网络理论、多元统计分析、应用回归分析等[1-9].本文论述利用行列式的计算方法解决一些初等数学问题,从而说明用高等数学理论与方法解决初等数学中较难的问题,其方法更简便,同时也更有技巧性[1].
一、利用行列式证明等式与不等式
根据行列式的性质,我们可以构造行列式来证明等式和不等式.下面分别列举一个例子来说明.
例1已知a+b+c=0,求证a3+b3+c3=3abc.
证明令D=a3+b3+c3-3abc,则
命题得证.
例2已知a≥b≥c≥0,求证b3a+c3b+a3c≤a3b+b3c+c3a.
证明令D=a3b+b3c+c3a-(b3a+c3b+a3c),则
=b(c-a)(b+c)(b-c)-a(c-b)(a+c)(a-c)
=(b-c)(a-c)(a+b+c)(a-c),
而a≥b≥c≥0,则D≥0,命题得证.
二、利用行列式分解因式
我们可以利用行列式的性质对多项式分解因式.下面列举一个例子来说明.
例3分解因式:(cd-ab)2-4bc(a-c)(b-d).
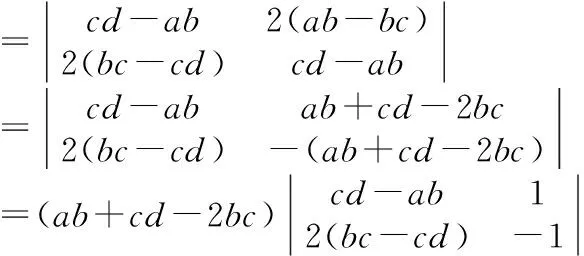
=(ab+cd-2bc)2.
三、行列式在几何中的应用
(一)用行列式表示直线方程、平面方程与圆的方程
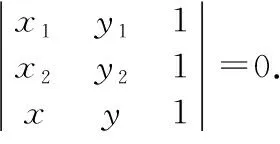
(1)

同理,若平面有三个不同的已知点Α(x1,y1),B(x2,y2),C(x3,y3),圆O过A,B,C,则圆O的方程为
(二)用行列式判别三线共点与三点共线
平面内三条互不平行的直线
L1:a1x+b1y+c1=0,
L2:a2x+b2y+c2=0,
L3:a3x+b3y+c3=0
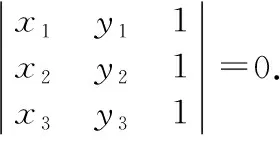
(三)用行列式表示三角形面积
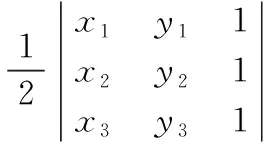
(2)
的绝对值.
(四)利用行列式表示平面法向量
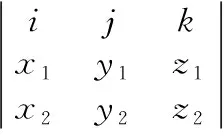
猜你喜欢
绵阳师范学院学报(2020年11期)2020-11-30 05:18:38
数学小灵通(1-2年级)(2020年9期)2020-10-27 03:24:26
新高考·高一数学(2018年5期)2018-11-22 11:03:52
乡村地理(2018年3期)2018-11-06 06:51:10
乡村地理(2018年4期)2018-03-23 01:53:38
商丘职业技术学院学报(2017年5期)2017-11-14 12:03:31
乡村地理(2017年4期)2017-09-18 02:53:52
小星星·阅读100分(低年级)(2017年1期)2017-01-20 19:20:46
考试周刊(2016年89期)2016-12-01 12:38:39
铜仁学院学报(2016年5期)2016-10-19 06:56:30

