让学习从“问题”开始

孙静 朱冬春

【摘 要】在教学中教师要关注学生发现和提出问题能力的培养。具体可以从以下几方面着手：让学生利用经验迁移，发现和提出问题；借助同伴互问互答，解决问题；充分利用知识间的联系，有效沟通问题；通过练习的拓展延伸，进一步升级问题。在提出和发现问题中经历知识再发现的过程，获得思维能力的发展。

【关键词】小学数学；发现和提出问题；策略

《义务教育数学课程标准（2011年版）》提出，要增强学生“发现和提出问题、分析和解决问题能力”，这无疑突显了增强学生发现和提出问题能力的重要性。应当这样认为，问题能力不仅可以让学生经历再发现的过程，而且可以使学生获得“数学化”和“再创造”的思维能力的发展。

究竟什么是发现问题和提出問题？基于数学的视角，笔者认为，发现问题、提出问题，就是用数学的视角观察、用数学的思维提问。当学生面对生活现象时，会自觉地应用数学的眼光进行观察，敏锐地捕捉其中的数学信息，“经过多方面、多角度的数学思维，从表面上看来没有联系的一些现象中找到数量或空间方面的某些联系或矛盾，并把这些联系或矛盾提炼出来，用数学语言、数学符号集中地以‘问题形态表述出来。”本文将结合学生的学习过程，从三个方面谈谈如何培养学生发现和提出问题的能力。

一、经验迁移，发现问题

已有的经验对于新的学习具有迁移作用。一方面，当已有经验形成正迁移时，学生可以通过发现知识之间的联系，提出问题，使旧的经验直接促进新知的生长；另一方面，如已有经验产生负迁移时，学生仍可以发现和提出两者内在的矛盾冲突，经多角度思考问题，在冲突的解决中使新旧知识得以系统化。

案例：《三角形的面积》导入环节教学片段

师引导学生复习平行四边形面积算法和推导方法。

师：平行四边形的面积我们已经会求了，今天我们要来研究三角形的面积，你有什么问题想问吗？

生1：三角形的面积怎么算？

生2：三角形能用割补法吗？

生3：三角形与平行四边形面积有什么区别？

通过回顾平行四边形的面积推导方法，引导学生发现和提出自己的问题。学生充分利用以前学习平行四边形时的活动经验，以旧引新，在自主的学习状态下产生强烈的问题意识，主动提出问题。所提问题，正是教学的重点和学习的难点。

数学知识之间紧密联系，某一领域的知识往往由简单到复杂，由低一层次发展到高一层次，前面学习的知识和方法往往对后续学习产生影响。教学时，我们可以引导学生基于已有学习经验，发现疑惑，提出疑难问题，让新知识的学习从问题开始。

二、同伴互问，解决问题

最好的“问”是由学习者自己来问，由学习者互相来问。学生在广泛观察，比较事实、现象的基础上，经过分析、综合事物或现象的本质属性，提出“是什么”“为什么”“怎么做”的问题。学生倾听同伴的想法，提出问题，带着问题在对话交流中学习，使问题得以解决。

案例：《三角形的面积》教学片段

学生通过自主探究，形成三角形面积转化的几种不同方法（如下图），教师组织全体学生逐一解读。

师：请大家仔细看看作品和算式，你看得明白吗？有没有问题要问他？

生1： 为什么除以2？

生2：前面两种方法算式一样，为什么图形不一样？

生3：后面两种方法为什么不用除以2？

生4：2×6的2，3×4的3是怎么来的？

随着学生的提问，全体学生一起逐个解决问题。

关于对前两种拼组法的理解，学生的问题聚焦在“怎么会想到这种方法？”因为学生在《平行四边形面积》一课中有了割补法的经历，那么学习三角形面积时首先想到的转化方法还是割补，学生在比较现象的基础上思维产生了矛盾，他们很难从割补转到拼组的方法上来。因而会将矛盾转化为疑问“为什么要除以2”“你怎么知道两个部分面积相等”等。当然，课堂上学生提出的疑问，借助同伴的解答，通过沿着三角形的高画一条辅助线的方法在图形上获得了理解。解决了面积相等的疑问，那么先计算平行四边形的面积6乘4，再除以2，学生也就明白了。

关于后两种割补法，学生的疑难点在于“怎么割补，”因为用割补法把三角形转化成平行四边形，需要用到中位线的知识，超过学生的认知范围。割补后如何寻找对应条件？对于学生来说又是一大挑战。如何帮助学生解决疑难？课堂上依旧借助生生互问互答，引导学生通过图式的沟通来解释算式的含义，学生自然发现在割补时都利用中点分割出小三角形再补成长方形，前一种方法是底乘高的一半，后一种方法是底的一半乘高。

在这个学习过程中，有的学生即便只想到一种转化方法，但在同伴的帮助下获得了更多的方法。学生经历了发现问题—解读问题—解决问题的过程，推进思维的深入。

三、沟通问题，发现联系

不同数学方法或知识虽然各有侧重，但在数学思想方法的统领下又常常表现出内在的整体性。发现联系，利用联系，可以有效地帮助学生沟通问题，促进学习，形成系统的知识结构。

案例：《三角形的面积》教学片段

教师通过课件引导回顾关于三角形面积的四种不同的转化和推导方法（如上图）。

师：观察转化后的图形和计算方法，你对前面的问题有什么新发现？

生1：三角形的面积计算都可以转化成平行四边形。

生2：前两种方法是拼组，后两种方法是割补。

生3：三角形的面积都可以用底×高÷2来计算。

学生经过分析、思考、综合，在寻找联系、提出新发现的过程中，进一步沟通了几种方法的内在联系，建立三角形面积的概念，理解了三角形面积计算的内涵，并将学生的思维引向深入。

再如教学《分数解决问题》时，教师给出的情景是“有一条公路，如果甲队单独修，3天完成；乙队单独修，6天完成。如果两队合修，多少天完成？”学生通过假设一个具体的路的总长，进行计算，解决问题。出现几种不同的方法：①6÷（6÷3+6÷6）=2（天）；②180÷（180÷3+180÷6）=2（天）；③600÷（600÷3+600÷6）=2（天）；④1÷（1÷3+1÷6）=2（天）。教师这样引导学生：“观察比较前3种方法，并与第4种把总长看作单位‘1来思考的方法进行比较，有什么发现？”学生发现，甲每天修的[13]不变，乙每天修的[16]不变，几种方法都是“工作总量÷甲乙工作效率之和=工作时间”。学生能积极主动地把符号所代表的新知识与自身认知结构中原有的观念加以联系，用联系的观点去沟通问题，从联系的角度去寻找共性，从而产生深层的认知。

四、延伸拓展，问题升级

有效的练习设计，也可以给学生创设条件提出和发现问题。例如《三角形的面积》一课的练习，要求学生在方格纸上画面积是6平方厘米的三角形，比比谁画得多。有的学生一下子画出很多（见右图），有的只画出一个，还有的学生画错了。因此学生自然产生疑问“有什么窍门吗？”“这样的三角形底和高是多少呢？” “是不是也可以先想一个平行四边形呢？”“确定了底和高，三角形的形状是不是只有一种呢？”学生在不断提问中理解，只要思考同底等高的三角形有无数种或先思考面积的2倍即12就简单了。在一项数学学习研究开展的整个过程中，都应当指向新的知识点引导学生发现和提出问题，为新的学习起航。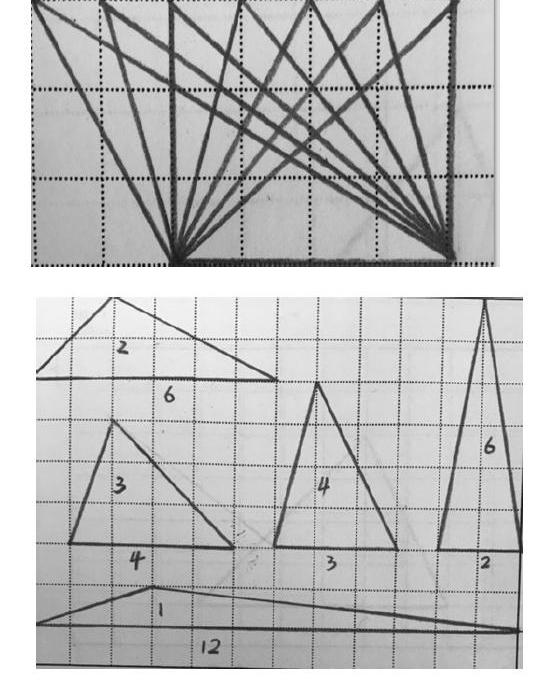

学贵有疑，学起于疑。思维以疑问为起点，有疑问才有思维，经过思维方能解疑。探索知识的过程总是从问题开始，又在问题中得到发展。学生经过多方面、多角度的数学思维，用数学语言将“问题”表述出来，真实的学习也就发生了。

参考文献：

[1]郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，2012.

[2]赵瑞生.基于“理解类型层次理论”的教学设计[M].上海：上海教育出版社，2015.

（浙江省海寧市实验小学 314400）