一种利用霍尔导数曲线反求地层参数的新方法
冉令博,杨二龙
(东北石油大学 石油工程学院,黑龙江 大庆 163318)
霍尔曲线法由霍尔于1963年提出,布尔等人于1989年提出近似解析方法,根据注入流体在霍尔曲线图上的不同直线段斜率,体现了各注入时期渗流阻力变化,其变化幅度反映了注聚合物的有效性[1]。H. Ferreira等[2]研究发现,水平注水井与直井的霍尔曲线图存在明显不同。为了分析注采井间储层动态特征,B. Izgec等[3-7]提出了改进霍尔曲线法(MHA),与常规的霍尔曲线相比,加入了积分的解析解与数值解两条曲线,通过霍尔积分导数曲线与霍尔积分曲线的相对位置可以判断任意时刻地层孔道动态特征,但MHA方法只能定性的识别孔道特征,而且实际生产中工作制度经常改变,这与改进霍尔曲线法采用的理想模型有所不同,公式中包含与注入参数有关的项易受到工作制度改变而产生误差。目前国内外对霍尔曲线进行了许多研究[8-13],但还没有学者应用霍尔曲线求取地层参数定量识别孔道特征。本文在MHA方法的基础上提出修正系数,并根据生产数据对其进行修正,进而求取地层渗透率定量识别储层孔道特征。
1 改进霍尔曲线法的修正
改进霍尔曲线法(MHA)是在同一个坐标系中绘制出霍尔积分曲线,以及霍尔积分导数的数值解和解析解这三条曲线,并且数值解与解析解曲线相重合。一般情况下,导数曲线叠加在积分曲线上,但当渗透率变大时就发生了分离,积分曲线和导数曲线分离的距离还可定性识别孔道特征(见图1)。

图1 改进霍尔曲线法示意图Fig.1 Modified Hall curve method
利用大庆油田某区块一口注入井的生产资料数据绘制改进霍尔曲线,发现霍尔积分导数解析解与数值解曲线趋势一致,但并不重合(见图2),因此需对MHA公式进行修正。霍尔积分解析解(见式(3))中拟表皮系数S*的计算过程含有参数Δtsup(见式(1)),Δtsup由注入量和时间计算得到,工作制度的改变会对其造成影响,为了避免工作制度的改变对解析解的影响,对解析解中与工作制度有关的Δtsup进行修正。
(1)
将区块各井的月注入量及累积产水量代入式(2),求出一系列时间点的积分导数的数值解DHIn。
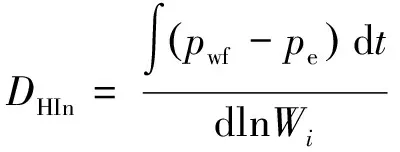
(2)
式中,pwf为井底流压,MPa;pe为油水界面压力,MPa;Wi为累积注水量,t;IH为霍尔积分,MPa·月;t为注入时间,月;i为注入速度,t/月。

图2 修正前改进霍尔曲线Fig.2 Uncorrected modified Hall curve
将地层动静态参数及生产数据代入到式(4)—(8),并结合式(3),令DHIn=DHI,建立等式求出Δtsup',最后根据本文提出的系数修正公式(9)得到修正系数β。
DHI=α1Wi[ln(re/rw)+S*]
(3)
导数解析解DHI中各参数计算公式如式(4)—(8):
(8)
其中,re为驱替前缘半径,m;rw为井筒半径,m;μ为黏度,mPa·s;k为渗透率,mD;h为储层厚度,m;φ为孔隙度;ct为综合压缩系数,MPa-1;qn为月注水量,t;Sor为残余油饱和度。
式(9)为本文提出的修正系数公式:
(9)
其中,n为总井数,口。
得到计算参数b的新公式为:
(10)
2 地层参数求解
将大庆油田某区块的生产数据代入式(1),并利用DHIn=DHI建立等式求出Δtsup',然后根据式(9)计算出该区块的修正系数为1.2,则修正后的参数b计算公式为:
(11)
利用修正后的解析解公式计算出DHI,同DHIn及霍尔积分绘制在同一坐标系下,DHI与DHIn两条曲线重合(见图3),可见修正结果较好。
将某井的月注入量及累积产水量代入式(2),求出霍尔积分导数的数值解DHIn,将渗透率k作为未知数带入式(3)—(5)及式(7)、(8),结合修正后得到的式(11)求得DHI,令DHIn=DHI,即可得到地层渗透率k。

图3 修正后改进霍尔曲线Fig.3 Corrected modified Hall curve
3 应用实例
大庆油田某区块有水井42口,将每口水井的生产数据(某单井生产数据见表1)代入式(2)进行计算,然后将计算结果代入修正后的式(3),求得各井地层渗透率,并将所求结果与各井实际地层渗透率相比较(见图4),发现误差小于8%的井占全区总井数的91.4%,验证本文所提修正方法合理有效,同时能够准确计算地层渗透率。
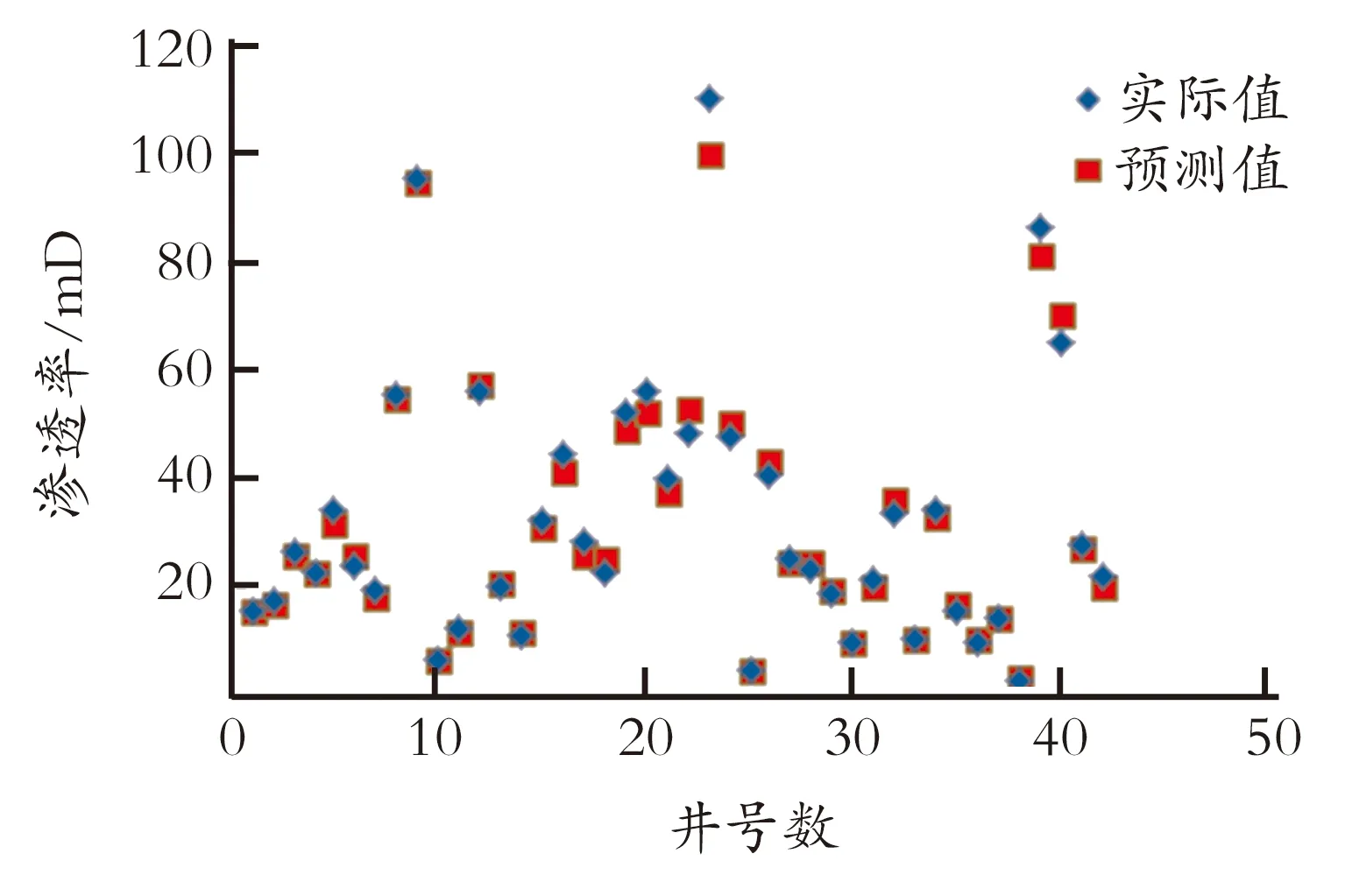
图4 渗透率实际值与预测值对比Fig.4 Actual permeability and predicted permeability
某注入井井筒半径0.304 8 m,原油黏度6.7 mPa·s,原油体积系数1.115,原始地层压力11.08 MPa,残余油饱和度0.3,综合压缩系数0.000 84 MPa-1,孔隙度0.2,砂岩厚度29.7 m,渗透率15.7 mD。

表1 某注入井部分生产数据Table1 Production data of one injection well
根据计算结果绘制霍尔曲线如图5所示。由图5可知,在累积注水量达到5.4×104t时储层开始出现优势渗流通道,表明储层在长期注水冲刷下孔吼结构发生改变,易产生大孔道。该井投产初期周围实际地层渗透率为15.70 mD,该井初期周围地层渗透率为16.41 mD,误差4.52%,误差较小。计算累积注水量为(5.4~10.0)×104t的地层平均渗透率为36.77 mD,渗透率较投产初期明显增加,也说明地层经注入水长期冲刷形成高渗通道。

图5 某注入井修正后改进霍尔曲线示意图Fig.5 Corrected modified Hall curve of one injection well
4 结论
(1)为避免工作制度对改进霍尔曲线的影响,利用本文提出的修正系数,通过区块实际生产数据对B. Izgec的改进霍尔曲线法进行修正,确定Δtsup的修正系数β为1.2,修正后的曲线更加符合油田实际生产特征。
(2)将全区水井投产初期数据计算出的各井渗透率与实际水井地层渗透率相比较,误差小于8%的井占总井数的91.4%,验证本方法合理有效,对指导油田开发方案调整,进一步认识储层状况有着重要意义。
(3)利用修正后的改进霍尔曲线公式预测某注入井后期地层渗透率为36.77 mD,较投产初期16.41 mD明显增大,说明地层渗透率变大,出现优势渗流通道,与改进霍尔曲线规律一致,可定量的识别优势渗流通道的存在。

