致密砂岩储层孔隙结构多重分形特征定量表征
姜 鹏,贾慧敏,马世忠
(1.东北石油大学 地球科学学院,黑龙江 大庆 163000;2.中石油华北油田 山西煤层气勘探开发分公司,山西 晋城 046000)
致密砂岩油、气为我国重要的非常规油气资源,其储层孔隙结构对油气渗流具有重要的影响,需精细、定量表征,分形几何为储层孔隙结构的定量表征提供了途径[1]。贺承祖等[2]提出了砂岩孔隙结构分形维数计算的方法,之后何琰等[3]、李中锋等[4]对不同区块砂岩孔隙结构的分形特征进行了研究。马新仿等[5]提出了用分段回归方法计算分形维数。尹帅等[6]对常规及非常规储层岩石分形特征进行了研究,并分析了其对渗透率的影响。牛鑫磊等[7]对煤系地层中致密砂岩的分形特征进行了研究,认为部分砂岩分形维数具有两段分形特征。孙瑛莹[8]、吴浩等[9]研究了不同类型砂岩储层孔隙结构的分形特征。目前对致密砂岩储层分形特征的研究未重视其多重分形特征,仍然延续了以往一段分形或两段分形的方法,未对砂岩孔隙结构的分形区间进行深入研究,对致密岩储层孔隙结构的描述不够精细。本文采用压汞方法对大庆油田外围某致密储层FY油层的孔隙结构特征进行了研究,重点从分形区间和分形维数角度研究了不同类型储层孔隙结构多重分形特征,以期为致密砂岩储层孔隙结构的精细定量描述提供借鉴。
1 基于压汞数据的孔隙结构分形特征表征
贺承祖等[2]计算得到砂岩孔隙结构分形特征定量表征模型:
lgSw=(Df-3)lgpc-(Df-3)lgpmin
(1)
式中,pmin为最大孔隙所对应的毛细管压力,Sw为湿相饱和度(Sw=1-SHg),pc为毛细管压力,Df为分形维数。
由式(1)可知,在双对数坐标中,毛细管压力(pc)和湿相饱和度(Sw)成一条直线,该直线的斜率为Df-3,进而可以求出分形维数。
马新仿等[5]提出利用分段回归的方法计算岩样的分形维数,更能反映岩样孔隙结构微观特征,因此,根据不同岩样孔隙结构的实际特征,在lgpc-lgSw直角坐标中,利用最小二乘法划分了各岩样的分形区间,并根据分形区间分段进行线性回归,分别计算了不同分形区间的分形维数。并采用李振等[10]提出的方法,以各个分形区间孔隙体积占总孔隙体积的百分比进行加权平均,求出各岩样的综合分形维数。
2 压汞实验及结果
2.1 实验岩样制备
选择大庆油田外围FY致密储层岩样,加工成5.0 cm×2.5 cm规格的岩柱,并用甲苯将岩样抽提、洗净、烘干。其中1#、2#、3#、4#岩样分别选自该I、II、III、IV类储层。
2.2 实验过程
首先利用QT-STY-2型气体渗透率测定仪和QKY-2型气体孔隙度测试仪,分别测定各岩样渗透率、孔隙度,结果见表1。

表1 实验岩样基本物性参数Table 1 The basic physical parameters of experimental samples
在室温下(20 ℃)利用美国康塔仪器公司的PoreMaster-60压汞仪开展高压压汞实验,实验严格按照石油行业标准《岩石毛管压力曲线的测定》(SY/TSP346—2005)进行操作。
2.3 实验结果
图1为4块岩样高压压汞曲线,表2为4块岩样压汞实验结果数据。图1和表2表明,在汞饱和度-毛细管压力半对数图中,1#岩样压汞曲线位于左下方,水平段较长,进汞饱和度较高,排驱压力较小,表明1#岩样孔隙结构相对简单,孔隙结构均质性较强,物性条件相对较好;4#岩样压汞曲线位于右上方,无水平段,进汞饱和度低,排驱压力较高,表明4#岩样孔隙结构复杂,分选性差,非均质性强,物性条件最差;2#、3#岩样位于相对中间位置,进汞饱和度和排驱压力适中,物性条件好于4#岩样,差于1#岩样。
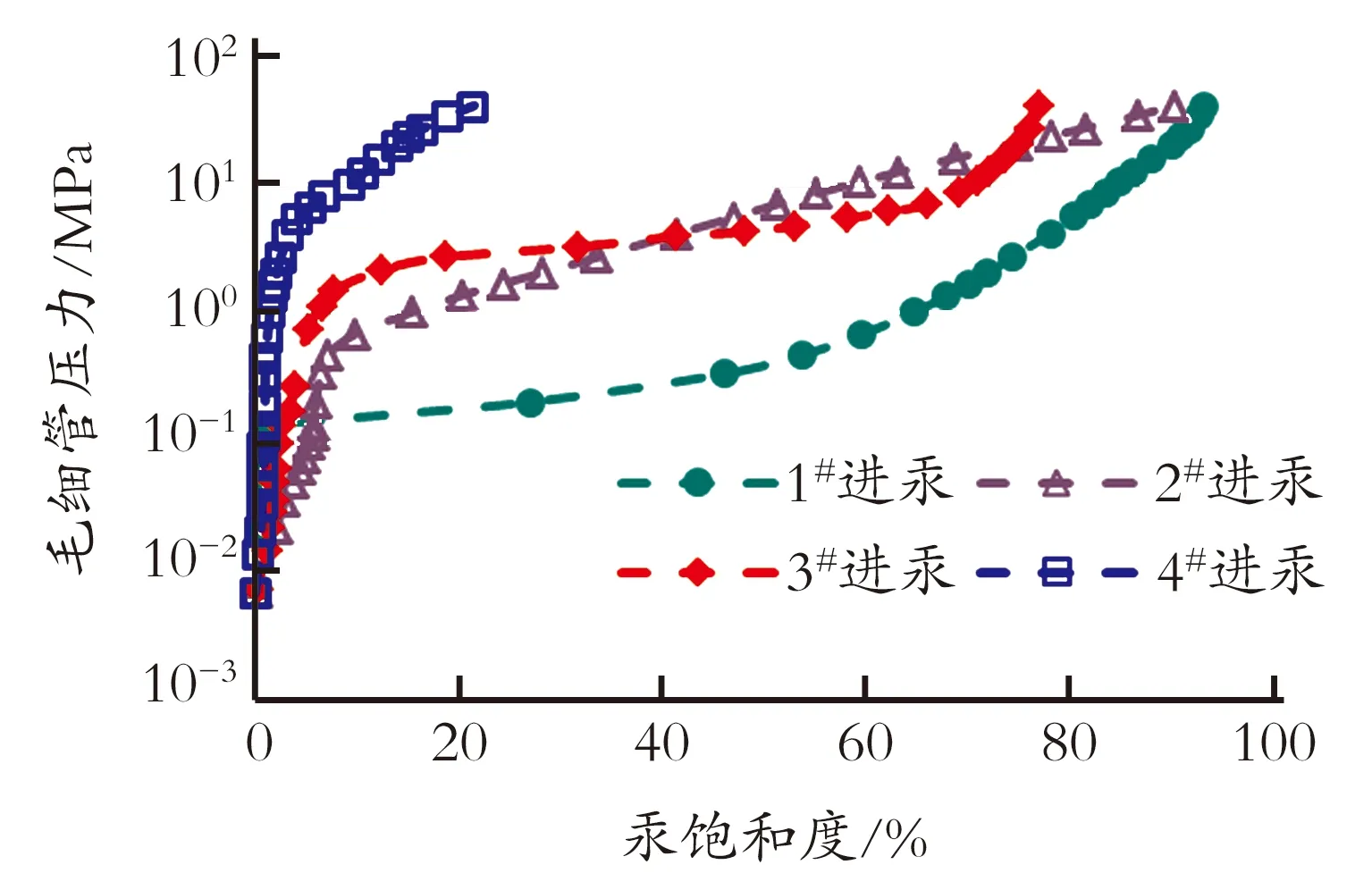
图1 实验岩样压汞曲线Fig.1 Mercury intrusion cures of test samples
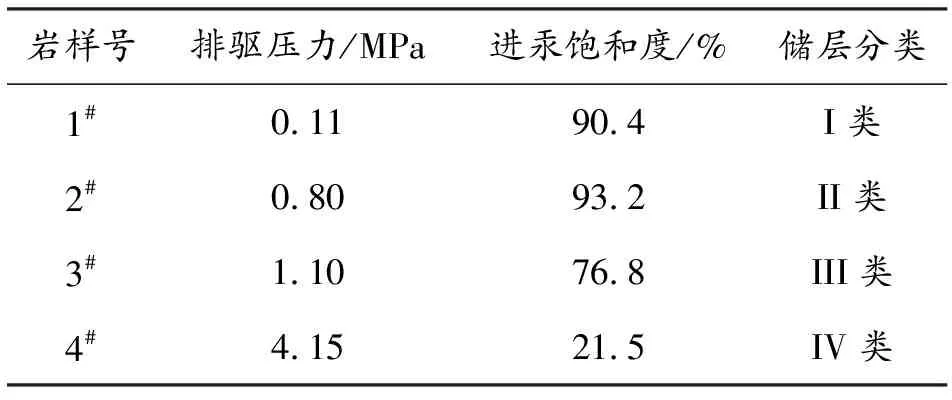
表2 实验岩样压汞实验结果Table 2 The outcome of mercury intrusion experiments for sandstone samples
3 孔隙结构多重分形特征
根据第1节中提出的方法,对4块岩样压汞实验结果进行处理,结果见图2、表3。

图2 致密砂岩岩样孔隙结构分形特征Fig.2 Fractal features of pore structure for tight sandstone samples
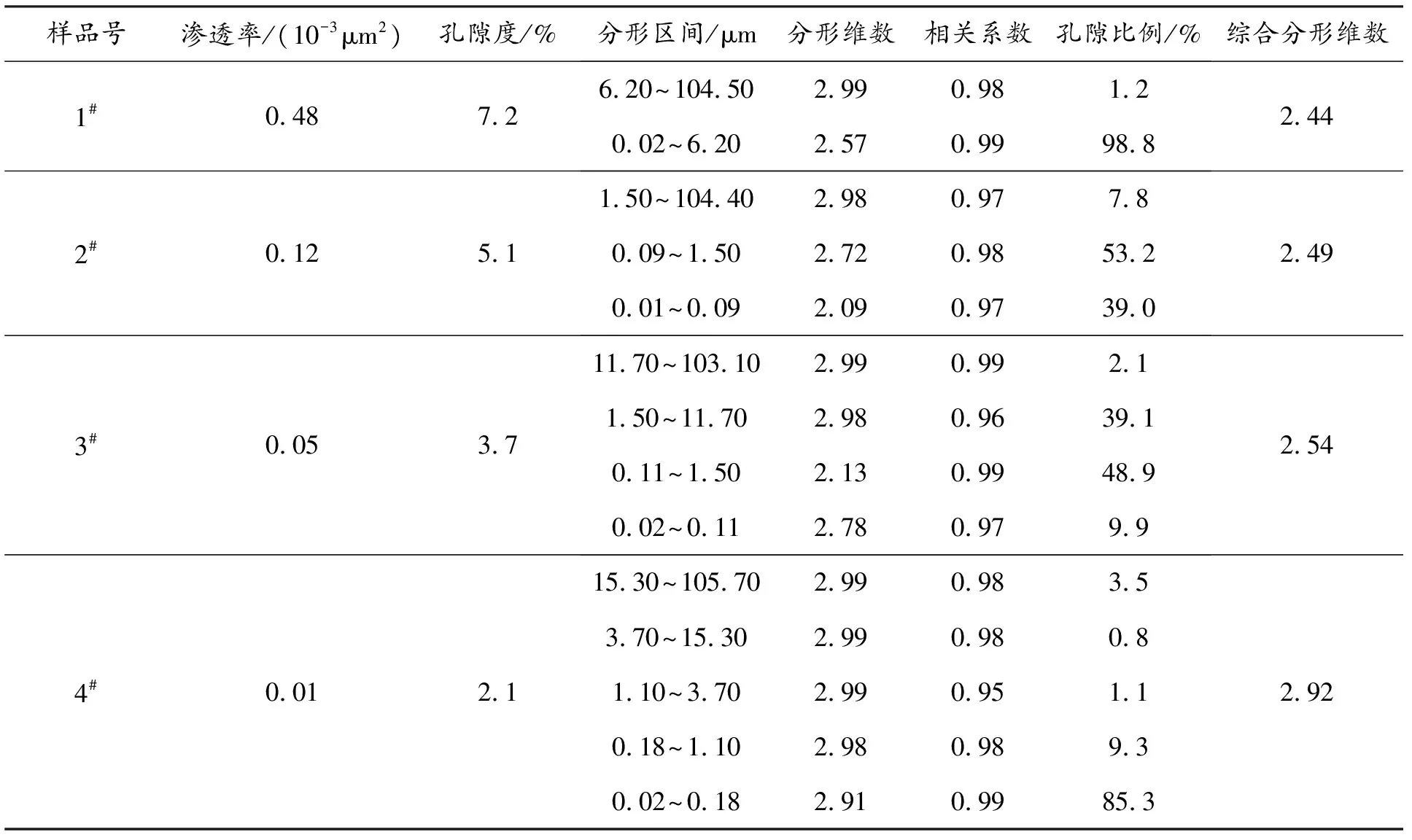
表3 实验岩样基本参数及孔隙结构分形特征Table 3 The basic physical parameters and fractal features of pore structure for experimental samples
3.1 多重分形区间
由图2可见,同一致密砂岩岩样,在整个微观孔隙空间上具有不同的分形区间,即致密砂岩微观孔隙结构具有多重分形特征。如1#岩样有2个分形区间,分别为0.02~6.20 μm和6.20~104.50 μm;而4#岩样则具有5个分形区间,分别为0.02~0.18 μm、0.18~1.10 μm、1.10~3.70 μm、3.70~15.30 μm、15.30~105.70 μm。多重分形可以更加精细地表征储层不同级别微观孔隙结构,如图3(a)所示,以6.20 μm为界限,1#岩样孔隙半径分布曲线呈双峰型,每个峰对应一个分形区间。同样如图3(d)所示,分别以15.30、3.70、1.10 μm和0.18 μm为界限,4#岩样孔隙半径分布曲线呈五峰型。因此多重分形既是致密砂岩微观孔隙结构的客观特征,也是其精细表征的有效方法。
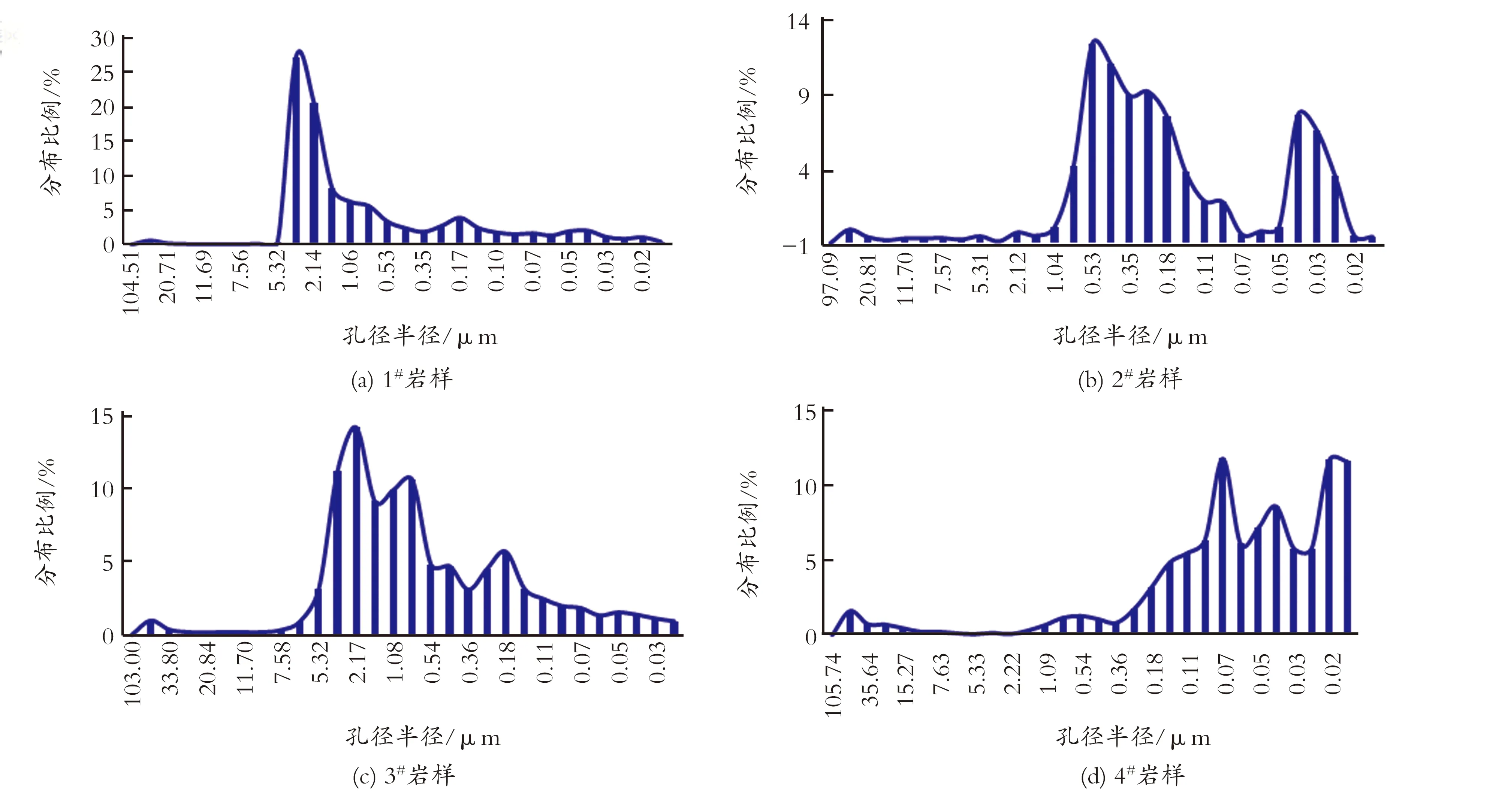
图3 致密砂岩岩样孔隙半径分布曲线Fig.3 The distribution curve of pore radius for tight sandstone samples
不同岩样孔隙分形区间个数不同。由图1可知,在孔隙半径为0.02~106 μm,1#、2#、3#、4#岩样,分别具有2、3、4、5个分形区间。同时,表3表明,不同岩样的分形区间个数随渗透率和孔隙度的降低而增加,这表明储层物性条件越差,分形区间越多。另外,图3表明,分形区间个数与孔隙半径分布曲线峰值个数相同,因此,砂岩微观孔隙结构分形区间个数可以作为储层评价的关键参数,1#、2#、3#、4#岩样分形区间增多,孔隙结构非均质性增强,且储层物性条件依次变差。
由表3可知,不同岩样分形区间不存在统一的界限,如1#岩样的分形区间界限为6.20 μm,2#岩样的分形区间界限分别为1.50、0.09 μm,3#岩样的分形区间界限分别为11.70、1.50、0.11 μm,4#岩样的分形区间界限分别为15.30、3.70、1.10、0.18 μm。因此,通过孔隙半径对致密砂岩孔隙进行统一划分不能准确反映微观孔隙结构分形特征,不同砂岩孔隙结构分形区间具有独特性和差异性。
3.2 多重分形维数
表3中同一岩样不同分形区间的分形维数表明,孔隙半径越大的分形区间其分形维数越大,这是因为孔隙半径越大,分形区间内孔隙结构的非均质性越强。如图3(b)所示,2#岩样孔隙半径为1.50~104.40 μm时,峰值处(20.80 μm)孔隙比例仅占该区间全部孔隙的20%左右,孔隙大小分布较为分散,孔隙分选性较差,非均质性强,因此分形维数最大,为2.98;孔隙半径为0.09~1.50 μm时,峰值处(0.42~0.53 μm)孔隙比例达到60%左右,而孔隙半径为0.01~0.09 μm时,峰值处(0.03~0.04 μm)孔隙比例达到87%以上,孔隙大小分布越来越集中,均质性增强,分形维数依次降低为2.72和2.09。
由表3可知,对于不同岩样,储层渗透率、孔隙度越小,分形区间越多,岩样的综合分形维数越大。这表明综合分形维数能够表征岩样微观孔隙结构的非均质性,综合分形维数越大孔隙结构非均质性越强,储层物性条件越差。如4#岩样综合分形维数为2.92,其孔隙半径分布曲线有5个峰值,孔隙非均质性强,且孔隙半径主要分布在0.02~0.18 μm,比例高达85.3%,储层物性条件较差。
4 结论
(1) 致密砂岩微观孔隙结构具有多重分形特征,即在整个微观孔隙空间上具有不同的分形区间,根据储层孔隙结构多重分形特征可以进行储层评价,划分储层类别。
(2) 孔隙结构分形区间个数能够表征储层非均质性,分形区间个数越多,非均质性越强,物性越差。不同岩样孔隙分形区间个数不同,分形区间个数与孔隙半径分布曲线峰值个数相同,并随着渗透率、孔隙度的降低而增加。
(3) 同一岩样,孔隙半径越大的分形区间的分形维数越大,分形区间内孔隙结构非均质性越强。不同岩样的综合分形维数越大,分形区间越多,储层渗透率、孔隙度越小。储层综合分形维数可作为储层评价的重要指标。

