追根溯源，解法自然成——以一道习题谈解题教学

◎王永生

(江苏省南京市六合区棠城学校，江苏　南京　211512)

一、背　景

“明明讲清了，学生为什么不会做？”一堂精彩的数学解题课下来，常常听到很多同仁发出这样的感慨，出现这样的局面，到底问题在哪儿呢？笔者以为：不少教师在进行解题教学时，往往只是站在教师角度一味地将自己的理解灌输给学生，而没能考虑到引导学生怎么想，师生之间没有形成有效的沟通路径，整个教学过程自然演变成教师单向的“讲清”，学生无奈地接受，效果自然不好.

笔者也在反思，很多数学问题的解决并不是一蹴而就的，它需要经历信息的输入与加工、思维的辩证与调整以及解法的选择与改进.因此，面对一个数学问题，先确定问题所涉及的重要知识点，并以此进行知识本源的联想，顺藤摸瓜，提出可能解决问题的方向，再适当地调整、修改和优化，让解法自然生成.在教学八上轴对称图形一道习题时我进行了一次尝试并对此深有体会.

二、教学片段

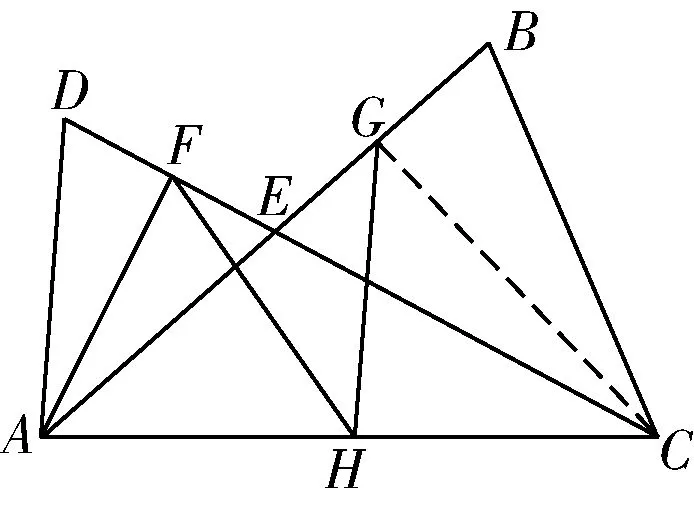
例题如图所示，AB，CD交于点E，AD=AE，CB=CE，F，G，H分别是DE，BE，AC的中点.求证：FH=GH.

很多学生审完题后，都被这复杂的图形和烦冗的条件弄得不知所措，学生解题能力提高关键是教会学生怎么想，于是先向学生指出：从知识转化角度，数学习题一般都要运用所学过的知识源加以解决，然后笔者开始引导学生思考：

问题1本题是求线段相等，那么现阶段已学过的求线段相等的有关知识有哪些？

相比之前绞尽脑汁的思考，面对这一问题，学生纷纷作答，补充完善.生1：“全等三角形对应边相等”(知识源1)；生2：“等角对等边”(知识源2)；生3：“角平分线上的点到角两边距离相等”(知识源3)；生4：“线段垂直平分线上的点到线段两端距离相等”(知识源4)；生5：“线段间的和差关系及等量代换”(知识源5).

问题2这些知识源就是解决本题的思考方向和突破口，那么本题应该选用哪个知识源来求线段FH=GH？

考虑到H为AC中点，AH=CH，学生首先考虑知识源1，连接CG，构造△GHC，试图证△GHC≌△FHA，但始终找不到其他条件，如果考虑知识源2，连接FG，将线段FH、GH构造到△FHG，但想证角等更不容易；而知识源3、4更是建立在特定的几何图形中才能应用起来，显然FH、GH又不是这样特殊的线段，基于知识本源的思考，一下陷入困境，这时我深知断不可急于给出解法，因为对思路的探索过程毫无疑问应是解题教学的重中之重，不然之前所做的一切就白费了，整个教学也就再次回归到“怎么做”的模式，这里一定要舍得花时间，于是我开始引导学生关注题干条件能得到什么或关联哪些知识点？

问题3抓住条件AD=AE，F是DE的中点，你能想到什么知识？

学生经过这一提示，很快会关联到等腰三角形“三线合一”的性质，易得AF⊥DC，图中也就出现了基本图形直角三角形，我顺势提出问题.

问题4关注问题线段和所得结论之间的关系，你又能联想到什么知识点？

反思本例的教学，当看到学生陷入思维僵局的时候，我没有急于给出解答的方法，而是引导学生追根溯源，先让学生回顾初中阶段“求线段相等”的有关知识源，这样学生一下有了思考的方向，尽管相关的知识源很多，但因为有些知识源适用的范围有限制，学生们不难有所取舍，选择合适的知识源形成一定的思路，后来在探索过程中再次遇到障碍，这时我没有因为时间的原因，加快讲解，而是选择在一旁适时进行思维调控，慢慢引导学生对题中条件逐一剖析，关联出有关基本图形、基本知识点，最终在这样不断的知识关联中解法自然生成，这也正体现了“数学问题一般都是借助已有知识经验加以解决”的转化思想.

三、教后反思

由此可见，多数情况下，要解答一个数学问题，探寻正确解法的过程并非一帆风顺，而是曲折起伏，但是探寻正确解法的思路却是“有序可循”：那就是从分析题目的已知入手，从一些具体条件展开联想，尽量使条件的指向丰富，提取出一些有用信息，然后再对照问题需“要求什么，必须有什么……”进行分析，追溯和这一问题有关的知识源有哪些？再结合题意选择一个知识源作为思考的方向，如果确实不知所措，这时可以以题干条件关联程度近的知识点切入思考，看它是否给我们以启示，当发现还走不通时，再换与题干知识关联程度相对较远的知识点着手探究，直至生成正确解法.

总之，通过这种追根溯源的思维方式进行解题，往往能打开解决问题的思维通道，明确解决问题的思考方向，使学生形成良好的思维习惯，从而从根本上提升学生分析问题、解决问题的综合能力.