美国NAEP数学试题的认知水平分析及其启示*

余春妹　唐恒钧　杨光伟

(浙江师范大学教师教育学院 321004)

美国具有代表性的评价项目——NAEP(National Assessment of Educational Progress)的实施及其所产生的影响，与PISA、TIMSS一样，都表明国际组织及各国对教育发展、教育质量的状况和发展趋势给予了高度的重视.基础教育质量监测和评估是教育质量提升、进行国际教育质量比较、教育改革的重要抓手[1].基础教育质量监测、大规模的学业水平测试为教师、学校、相关教育行政部门改变教育教学方法和制定教育教学政策将提供一定的数据和依据.分析美国NAEP近六次公布的八年级数学样题对我国基础教育质量监测有一定的参考价值.

1　NAEP概况

美国的教育进展评估(National Assessment of Educational Progress，简称NAEP)，主要由国家评估管理委员会(National Assessment Governing Board,NAGB)和教育部下辖的教育统计中心(National Center for Education Statistics,NCES)共同完成[2].它是美国具有代表性的教育评估项目，主要评估学生对学校课程的掌握情况，向公众报告学生学业成就.NAEP的测试对象是4、8年级和12年级的学生.测试科目包括阅读、数学、科学、写作、艺术、公民、经济、地理和美国历史等9个学科[3].其中，数学、阅读和科学是最主要的测试科目.NAEP评价的类型可以按照不同的维度进行分类，如按评价层级可以分为全国评价、州级评价和城区评价，按时间可以分为短期评价和长期趋势评价[4].全国评价和州级评价至少每隔两年对4、8年级的学生数学和阅读进行评估.

NAEP测评框架的建立是政府、教育界、商界和公共部门等大量专家共同合作的成果，力图反映美国社会对数学素养的基本要求，力图反映学生在不同年级所需要具备的数学知识、技能和潜力，提供关于美国学生对于数学在日常生活中的应用能力的基本信息[5].因此，对基于NAEP测评框架编制的试题进行分析能够让我们更加了解美国对学生数学能力、数学素养的要求.

NAEP考察学生数学课程方面学业成就时，设定了数学课程中的课程内容和数学认知能力的评估维度.八年级数学内容包括数的性质和运算(20%)、测量(15%)、几何(20%)、数据统计和概率(15%)、代数(30%).NAEP通过题目的复杂性评估学生的数学思维，将复杂性区分为低(20%)、中(50%)、高(25%)三个水平，并通过“量尺分数”(scale score)评价学生的数学表现.量尺分数是指将接受测验者在该项测验答对的题数，依据测验原理订定数学公式，并依据此数学公式转换成可以在测验之间、考生之间相互比较的分数.4、8年级数学的量尺区间是 0～500分.美国NAEP项目还将测量结果以国家报告卡的形式(The Nation’s Report Card)向公众报告.从时间角度划分，NAEP数学评估报告分为趋势评估报告和主评估报告；按评估的层级划分为全国评估报告、州级评估报告和城区评估报告.NAEP数学评价还在内容和年级方面对计算器的使用作了要求.

NAEP的试题包括学科测验和背景调查问卷两大部分.学科测验是依据评价框架中规定的内容领域进行编制，测量不同年级学生应达到的知识和能力水平[6].NAEP学科试题类型包括：多项选择题( multiple-choice items) 、简单建构反应问题( short-constructed response) 、扩展建构反应问题( extended-constructed response)[7].其中，多项选择题即给出多个选项选择其中一项；简单建构反应问题类似于简答题，要求学生根据题目给出数字等简短性的回答；扩展建构反应问题类似于拓展性开放题，不仅要求学生给出答案，还要求学生做出解释.八年级数学多项选择题占总试题的50%，建构反应问题占50%.背景调查问卷一般为选择题，涉及学生的基本信息及学生学习和生活的背景信息，主要针对学生、学校、教师进行问卷调查，为分析学生学业成就提供背景信息.

由于NAEP并没有公布全部试题，因此研究以NAEP官网[8]公布的八年级数学样题作为分析对象.

2　数学认知水平分析框架

教育目标既为教与学指明了方向，也是教育教学、教育评价等方面的依据.基于此，本研究将采用教育目标分类学的已有框架分析NAEP试题.布卢姆把认知目标分为：知识、领会、运用、分析、综合、评价[9].威尔逊(S.M. Wilson)引入布卢姆教育目标分类原则，将数学学科的认知目标划分为计算、领会、运用、分析4个层次.这里的“计算”包括了布卢姆认知目标的“知识”；“分析”相当于布卢姆认知目标的“分析、综合、评价”[10].国内顾泠沅借鉴国外研究经验和成果，结合本国的教育教学现状，对教学目标分层进行了探索.

顾泠沅先后两次(1990、2007)组织专门力量在上海市青浦区(原为县)进行大样本测试，从初中二年级学生在数学学习中大量外显行为所表征的教学目标中析取其内隐的主要因素，由此确定目标框架的层次并研究分类的连续性[11]，将数学教学目标分为四个层次：计算、概念、领会、分析.这四个层次总体上划分为记忆、理解两个不同思维水平.记忆包括操作性记忆水平和概念性记忆水平；理解包括说明性理解水平和探究性理解水平.

因此顾泠沅将学生数学认知分为四个水平：水平1——操作性记忆水平，计算；水平2——概念性记忆水平，概念；水平3——说明性理解水平，领会；水平4——探究性理解水平，分析.其中水平1、2(记忆水平)属于较低认知水平，水平3、4(理解水平)属于较高认知水平[12]，水平4(探究性理解水平)通常称作高认知水平[13].

为了更有操作性，需要将四个数学认知水平在NAEP试题具体化.

水平1——计算，属于操作性记忆水平.它是指学生按照课本要求的程序或步骤进行基本计算或者对问题中的元素进行常规操作(包括几何中的基本作图).这里表现为学生能够根据已经学习过的程序或步骤进行简单的计算，或者根据题目要求进行基本的几何作图.例如，2003年第一题“计算238+462的和”；2009年19题“下面哪个方程与方程2x+6=32 的解相同”.这里，只需按照基本加法计算程序即可求出.又如，2013年第35题“画出下面菱形的对称轴”，学生只要根据画对称轴的程序、步骤操作即可.

水平2——概念，属于概念性记忆水平.这一水平表现为用与课本一致或几乎完全一样的方式回忆或者复述定义、概念、命题、规则、表达形式或者数学事实，或者呈现已经学习过的数学事实或术语、基本概念的含义.鉴于美国NAEP试题对概念本身考查较少，例如“哪些是一元二次方程”此类题目出现少，主要是关注学生运用概念、原则、定理等回答数学问题或者解决实际问题.因此，这里表现为学生回忆或者呈现已学过的数学定义、基本概念、命题、规则等基础知识直接解决问题，即学生在知道、了解某数学定义、基本概念、数学事实等情况下即可完成任务.例如，2005年第4题“将图中纸筒沿虚线剪开，问剪开后的形状”，此题考查学生对棱柱侧面展开图的了解；2011年第8题“如果n是任意整数，下面哪个表达式一定是奇数”.该题考查数的性质和运算，小学已学偶数和奇数的特征，因此学生只需知道这一数学事实即可回答问题.

水平3——领会，属于说明性理解水平.它表现为学生不仅仅能回忆课本中的数学基础知识，还能理解复杂的数学概念、原理、数学结构等的内涵，能够根据逻辑关系读懂推理思路，对于题目字面背后的意义能够理解；可以根据课本例题解决常规的问题，包括对常规问题的不同变式作出比较，分析条件异同和类型，这些都是课堂中反复训练过的.这里表现为学生能够理解所学过的复杂数学概念、原理、法则、数学结构的内涵；对较为复杂的题目能够根据逻辑关系读懂推理思路，并运用所理解的内涵和推理解决常规问题.所谓“常规问题”指学生运用已学过的数学方式方法能够回答的问题，这些方式方法是学生在课堂上经常练习或者老师平时反复强调的.例如，2007年第8题：已知某自行车商店5天内每天卖出的数量及这些数量的平均数和众数，问哪个统计量更能代表此商店5天卖出的自行车数量并给予解释.此题考查学生运用统计量解决实际问题，学生需要理解平均数和众数的内涵和特征以及结合现实情境解决问题，因此属于第3认知水平.例如，2011年第24题“已知单位正方形的面积是25平方米，估计阴影部分图形的面积”，该题考查学生解不规则图形的能力，学生需要将不规则图形转换为规则图形，在理解几何图形性质和特征的情况下解决常规问题.

水平4——分析，属于探究性理解水平.这一水平表现为对于没有接触过或接触较少的非常规问题作出分析，把分析过程综合起来、通盘考虑，对于问题的解决过程或者方案可以作出判断或评价.具体表现为综合所学习的数学知识技能，分析、评价、创造性地解决“非常规问题”.所谓“非常规问题”是指与所学内容关联度不大的题目或者学生接触较少、不熟悉的题目归为非常规题目，也包括拓展性、一般化或特殊化的数学问题，以及复杂程度较高的数学推理题.例如，2011第43题“给出六个四位数，只有三个数是完整的，第四个数每个位值上的数字都未知，假如这六个数之和为奇数，请列举一个第四个数并给出理由”；2013年47题“如果s和t都是大于10的不同的素数，为什么s+t的和不可能是素数”.

3　NAEP试题数学认知水平分析

对美国NAEP 2003、2005、2007、2009、2011、2013近六年304道八年级数学样题[14]进行比较，从总体认知水平、不同数学领域间的对比、各年间的对比三个维度进行数学认知水平的比较分析.

3.1　总体水平

图1表明美国NAEP这六次试题水平2题目比例最高，其次是水平3，比例最低的是水平4的题目.这说明美国基础教育评价较注重基本概念的记忆、理解和运用.概念性水平高达47%，接近一半的题目是考查学生对定义、基本概念、命题、规则等基础知识的回忆、呈现.说明性理解水平占总水平的36.6%，说明考查学生对复杂概念、原理、法则等内涵的理解和对较为复杂的题目根据逻辑关系读懂推理思路，并运用所理解的内涵和推理解决常规问题的能力也比较重视.操作性记忆水平和探究性理解水平的题目量相似，但是水平1稍高于水平4，即四个数学认知水平中考查学生综合所学习的数学知识技能，分析、评价、创造性地解决非常规问题能力的试题最少.进一步，如将水平1和水平2的题目相加，美国NAEP的数学试题56.5%属于记忆层次，即超过一半的题目考查学生的操作性记忆和概念性记忆.

从数学总体认知水平的比较中，我们发现美国NAEP测试主要评价学生对数学基础知识和基本技能的掌握，要求学生能够回忆、呈现、理解数学基本概念、原则、数学事实等解决常规问题.

图1　试题总体认知水平

3.2　不同数学领域间的对比

从美国NAEP数学试题涵盖的内容领域来看，2003年到2013年期间公布的304道样题中，涉及“数”的题目有72个，“代数”的78个，“测量”的47个，“几何”的64个，“统计与概率”的43个.图2显示各内容领域水平2和水平3的试题远远多于水平1和水平4的试题，主要考查学生概念性记忆和说明性理解能力.“数”这部分内容，水平2的试题多于其他3个水平总和，重在考查学生回忆和呈现数的定义、基本概念、命题、表达形式等知识直接解决问题的能力.

图2　不同领域试题的认知水平

“数与几何领域”的题目概念性记忆水平比例最高，尤其是“数”，高达60%.“代数”、“数据统计和概率”的题目在水平2和水平3的比例相当，均在总题量的40%左右.“测量”领域水平3的题目多于其他内容领域.在四个内容领域的题目中，水平1和水平4比例较低，特别是探究性理解水平，“测量”的题目该水平仅占2.1%.相对来说，“数据统计与概率”在水平4的题目比例要高于同水平的其他内容领域，为总题量的9.4%；“代数与测量”在第1水平的题目要多于其他内容领域.这可能是因为“数据统计与概率”涉及对数据理解、分析及随机事件判断和决策能力，因此考查高水平的试题较多.而“代数与测量”的基本技能是运算与作图，学生只需按照一定程序或步骤进行基本的计算或作图即可完成任务.

3.3　各年试题间的对比

总体上，NAEP数学试题前三年四个水平的题目分布相似.即水平2的题目居多，尤其是2003年；其次是水平3，接着水平1，最后是水平4.2009和2011这两次NAEP的数学试题四层次认知水平分布雷同，即水平3试题量多于水平2，水平2试题量高于水平1，试题量最少的仍是水平4.2013年NAEP数学试题与前三次的前三个水平分布相似，不同的是2013年数学试题在探究性水平中的题目多于水平1，表明美国开始重视高认知水平题目的编制，重视考查学生综合所学知识灵活、创造性地解决非常规问题的能力及数学推理、探究能力.然而，2013年水平2的试题比水平3的试题多21.2%，这可能是因为水平4的题目增多或者是试题设计者考虑测试时间有限所致.

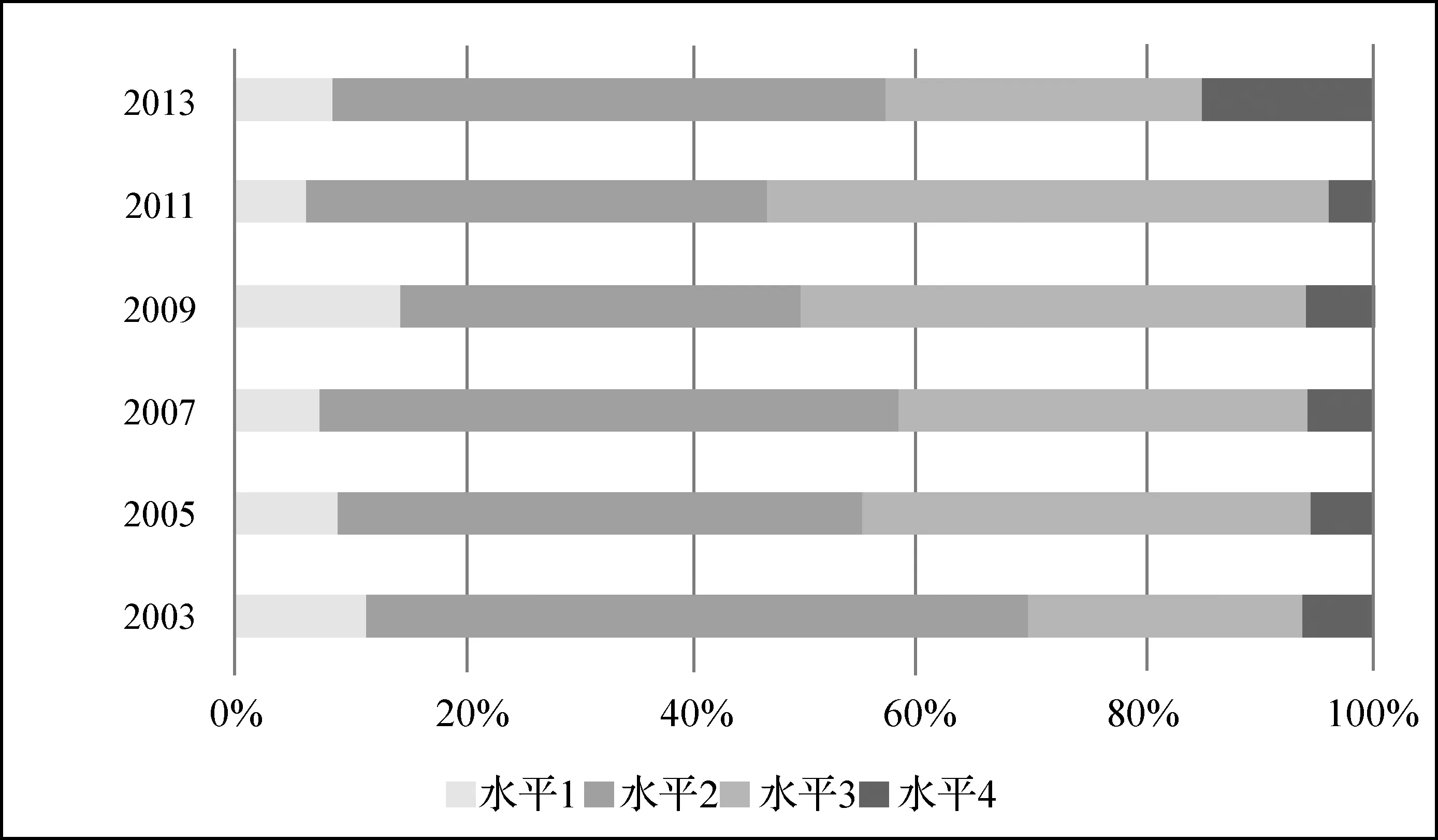
图3　不同年份试题的认知水平

通过各年间数学认知水平对比，发现水平2和水平3的题目仍然超过水平1和水平4.除2003、2009两年处于水平1的试题比例超过10%，其余均低于10%；2003、2005、2007、2013四年概念性记忆水平的试题比例接近或超过50%；说明性理解水平的题目比例仅2009、2011两年超过40%，其余均低于40%；除了2013年处于水平4的试题比例超过10%，其余均低于10%.

从总体而言，自2003年以来，理解层次的试题比例在不断上升.

4　启示

以上对NAEP试题在总体水平、不同内容领域、各年间变化三个层次的数学认知水平的比较分析，至少存在以下三个方面值得我国在开展基础教育质量监测时予以重视.

4.1　试题的设计应重点考察数学的核心概念

国际数学测试的一个重要特点是以核心数学知识为基本载体，建立评价框架及设计评价试题[15].NAEP数学试题评价的内容包括数、测量、几何、数据分析与概率、代数五个领域的核心知识、概念，它们反映了义务教育数学课程的核心内容.同时，美国NAEP对这些核心概念掌握程度提出了不同的要求，从上述数学认知水平的分析中可以看出.

数学这门科学包含不同分支的知识，数学教育应选择哪些内容作为课程内容、重点评价哪些数学知识、概念等方面都值得教育专家、教育研究者思考.对相关评价内容的确定，要关注有关知识领域的核心概念，这些知识领域是具有良好知识结构、能够体现学生的知识水平和理解能力的核心知识[16].PISA、TIMSS两大国际学生学业评价项目的数学评价内容均来自于数学学科的主要领域，即注重考查学生对数学核心概念的理解和应用能力.数学核心内容是数学基本技能的体现，同时也是数学思维的载体.试题设计重视考察数学核心知识、概念，有利于提高学生数学能力和数学思维水平.

另外，试题评价的内容应体现学科内容的时代性.即数学评价内容应有助于解决当前现实社会生活的问题，重点评价有利于个体当前及未来发展的核心概念.例如，在信息化、大数据时代，国际组织及各国都比较重视数据分析及概率统计观念和能力的考察.NAEP评价中“数据统计与概率”领域认知水平的分布表明美国对学生数学统计观念、随机概念的关注，重视培养学生运用数学统计与概率知识分析、解决问题的能力.同时我国2011版数学课程标准对抽样与数据分析、事件的概率的内容标准作了具体的阐述，也表明对数据分析与统计概念内容的重视.

因此，数学教育质量监测试题的设计应重点对数学核心知识、概念的考察.同时也要考虑数学内容的时代性，重视考察有利于学生解决当前或未来生活可能会遇到的有关数学问题的核心概念，提高学生解决问题能力.

4.2　学业成就评价应重点关注学生的数学基础

NAEP测试是美国具有代表性的教育评价项目，是国家性统考的学业水平测试[17].从NAEP分析的数据可以看出，其主要考考察学生基于课程的数学基础知识和基本技能，关注的是学生的数学基础.

学业成就评价，通常是指以国家课程标准为依据，以学业评价标准为准则，以学科内容为目标，运用质性和量化的方法，测评学生在一定时期内的知识、能力和情感的发展水平，并进行价值判断的过程[18].它的功能主要是评价学生学业水平；向教育行政部门、学校、家长反映学生的学业成就；诊断教育教学过程中的问题从而采取相关策略解决问题.因此，数学学业成就评价有别于选拔类的考试，它最终目的是提高数学教育质量和公民的数学素养.

目前我国比较典型的全国性测试要属中考、高考，但是这两类考试选拔性、甄别性的色彩比较浓，它们的评估结果难以代表我国大多数学生的数学学业成就.因此我国应重视建立体现大多数学生学业成就的教育质量评价体系，关注学生的数学基础，提高学生数学学习兴趣，进而促进“四基”课程目标的实现.这也体现了基础教育质量监测价值取向的定位问题，即基础教育的“基础性”问题[19].

4.3　教育质量监测应侧重于考察学生的数学思维水平

NAEP近六次数学评价水平2和水平3的试题比例较高，水平1和水平4的比例较低.同时，从图3我们能够发现从2005年至2011年NAEP的数学试题水平3、4题目比例在逐步提高，特别是2011年高达53%.2013年水平4——高认知水平的题目比以往增加一倍，重视探究理解能力的考察.从近年来NAEP试题来看，NAEP测验设计更加重视高级思维能力与复杂认知活动，加强对学生探索实践能力的评价，强调解决问题与数学探索能力[20].简而言之，NAEP数学评价侧重于考察学生的数学思维水平，重视学生数学思维的发展.

数学是一门逻辑性、抽象性、应用性比较强的学科.对数学的学习有利于学生思维水平的提高，同时学习数学也需要学生有一定的思维能力.数学学习要以学生的数学思维水平为前提，数学思维水平高必然促进数学学习成效[21].即数学学习与数学思维水平是相互联系的.

基础教育质量监测应侧重基础知识技能的考察，但是对于八年级学生来说应在掌握基础知识技能的基础上逐步提高数学思维水平，提高逻辑思维能力和推理、探究能力.高认知水平任务有助于发展学生高层次的思维能力[22].国外的学业成就调查，既重视知识的掌握，也重视能力特别是学生高级思维能力的发展[23].因此，在教育质量监测中我们应侧重数学思维水平的考察.同时，评价试题中应适当增设高认知水平的题目，提高学生数学思维水平，促进学生创新能力和解决问题能力的发展.

NAEP测评是比较全面、系统的教育评估体系， 它的测评工具是各领域学者和专家共同合作的成果.我国学业成就评价试题编制在借鉴其他国家经验的基础上，要符合本国教育发展规律和特点，在吸收、创新过程中建立我国基础教育质量监测体系.