基于椭圆的极点-极线性质构造非扭转叶片前缘的方法研究

王 跃曹利新谢耕樵

（1.大连理工大学机械工程学院；2.大连理工大学 电子信息与电气工程学部）

0　引言

叶轮作为透平机械的核心零件，在航空、航天、船舶等领域发挥着重要作用，因为叶片前缘的几何形状对进气端的流场产生影响，因而其对叶盘及整机的性能影响极大。为了简单便捷地进行实体建模和数控加工，传统的设计方法通常将叶片前缘形状设计为钝形和圆形[1]，但是近年来越来越多的实验和数值研究表明，采用椭圆形前缘可以明显改善叶片的气动性能，而且性能提高的益处远大于加工椭圆前缘的困难。初雷哲等[2]对叶轮前缘造型分别为钝头、圆形、椭圆形三种结构进行了数值模拟研究，发现椭圆形前缘与钝头、圆形造型相比，可以使压气机的通流能力、压比、效率达到最佳；同样也有实验结果验证了椭圆形前缘可以提高叶轮性能，Goodhand和Miller[3]针对低速单级压缩机，通过实验进行了叶片前缘形状对其性能影响的研究，结果表明：在保持其他零部件几何形状不变的情况下，长短轴比为3:1的椭圆形前缘较圆形前缘可使压缩机减少流动损失41%；董雷等[4]在使用数值模拟和实验验证中发现：在不同机器马赫数（Mu）下，不同长短轴比例的叶片椭圆前缘对叶片性能影响不同，达到最佳效果得视具体情况而定。

在叶片的设计阶段，通常给出了压力面与吸力面上两端点处的坐标和切矢，如何构造叶片的椭圆形前缘使其与叶片的压力面和吸力面光滑连接，目前相关的文献讨论很少。于源等[5]在分析叶片圆角构成的基础上，利用迭代法找到了各类型叶片圆角的圆心及半径，进而实现了前缘的几何造型。但工程中也有设计人员为了建模方便，利用三维建模软件首先构造叶片中性面，再按照叶片上各点的厚度对中性面进行偏置得到压力面与吸力面，然后直接利用面倒圆命令构造圆形前缘。这种简单的前缘构造方法无法满足叶片气动性能的要求。鉴于上述情况，本文以非扭转叶片前缘的构造为例，在深入研究椭圆极点极线性质的基础上，提出了一种新的椭圆形前缘构造方法。该方法可以满足设计人员对椭圆长短轴比例的要求，并可实现其与压力面和吸力面的光滑连接。

1　椭圆的极点-极线性质

为构造椭圆前缘，首先需要得到椭圆弧，一般绘制椭圆有两种方式[6]：间接法和直接法。间接法是通过二次曲线对数据点的无约束线性拟合，当二次曲线方程的参数符合椭圆的约束条件时，即可通过二次曲线方程化简得到椭圆的各个参数；直接法是通过椭圆方程对数据点进行非线性求解，得到椭圆的特征参数：椭圆中心坐标（x0，y0）、长短轴半径a、短轴半径b、长轴与x轴的夹角θ。上述两种方法都有局限性，如所需数据点比较多、间接法因噪声和失真干扰得到曲线不是椭圆、直接法存在解的收敛性问题等，因此这两种方法都不适用于叶片椭圆前缘的构造。考虑到构造叶片前缘条件的特殊性，本文采用椭圆极点-极线性质来反求椭圆。

参考图1，若P，Q和K为椭圆上的任意三点，椭圆在这三点处的切线分别交于A，B，C三点，弦PQ称作A点对应的极线，A点称作PQ对应的极点，三角形APQ为椭圆的极三角形。同理弦PK，QK分别称作B点、C点所对应的极线，B点、C点分别称作弦PK，QK的极点，三角形BPK，CQK同样为椭圆的极三角形。

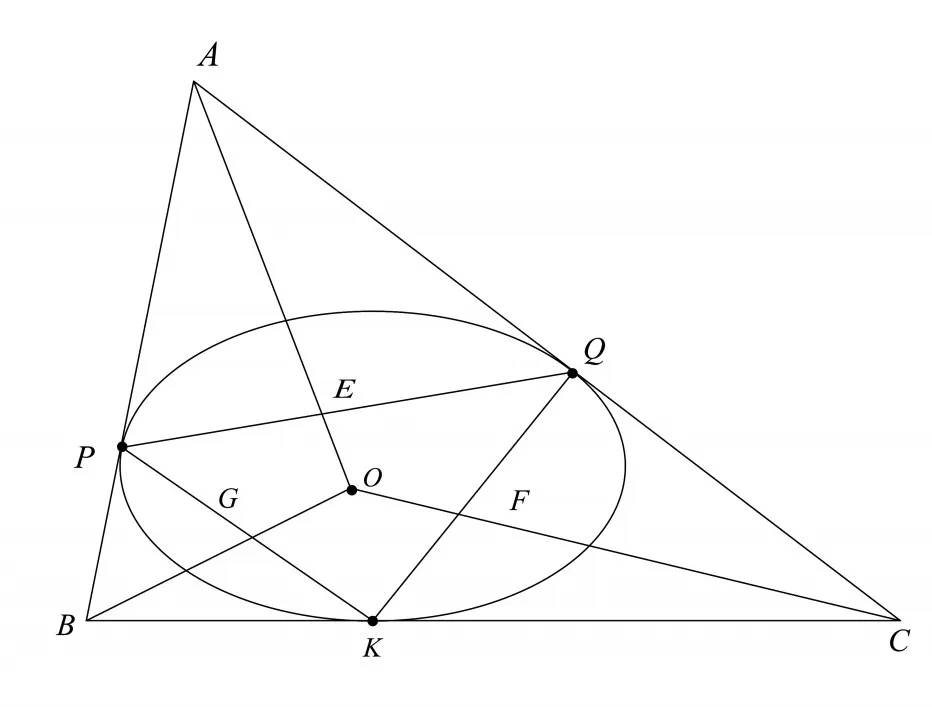
图1　椭圆的极点-极线性质Fig.1　Pole and polar properties of ellipse

二次曲线可以用极点和极线表示[7]，参考文献[6]中杨忠根通过推导给出椭圆（特殊二次曲线）的极点-极线性质如下：

性质如图1所示，极点A、极线PQ的中点E和椭圆中心O共线，同理3个极三角形APQ，BPK和CQK的极线边PQ，QK和KP上的中线延长线必共点于椭圆中心O。

由上述性质可知，三个点及过三个点的三条切线即可唯一确定一个椭圆。在构造非扭转叶片前缘时，通常只知道压力面与吸力面上叶片曲线两端点处的坐标及其切矢，若想利用椭圆的极点-极线性质构造椭圆弧，还缺少椭圆上一个点及该点处的切矢。另外，叶片设计人员通常希望通过椭圆的长短轴比例来控制椭圆的形状，下面讨论此种情况下椭圆弧的构造方法。

2　已知椭圆上两点及对应点切线构造椭圆弧的方法

叶片因其在工业领域的重要地位，众多学者对叶片模型构造、结构优化、加工工艺、结构强度、气动性能等方面进行了深入研究[8-11]，从而为建立叶片前缘奠定详实理论基础。在实际的叶片前缘建模过程中，遇到的情况通常是已知叶片压力面与吸力面上叶片曲线两端点处的坐标和切矢。对于非扭转型叶片，压力面与吸力面上叶片曲线两端点处的切矢共面，可以利用第2节中椭圆的极点极线性质推导该类叶片前缘的构造方法。

如图2所示，假设P，Q两点为压力面与吸力面上偏置盖盘曲线的两个端点，直线AB，AC为P，Q点处相应偏置盖盘曲线的切线（两切线共面），现要构造一个通过P，Q两点且与AB，AC相切的椭圆，同时椭圆的长短轴比例可控。

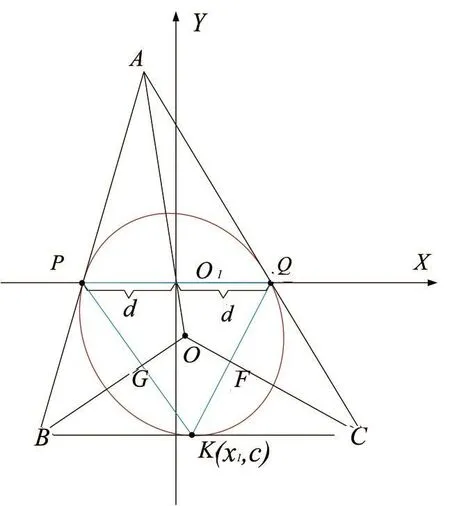
图2　根据椭圆上两点构造椭圆弧Fig.2　Constructing elliptical arc according to two given points

以直线AB和AC的交点A作为待构造椭圆的一个极点，PQ为A点对应的极线。以直线PQ为X轴、PQ中点坐标原点O1，按照右手定则建立如图2的平面坐标系{O1XY}。因此点P，Q坐标分别为（-d，0)，(d，0），d为线段PQ长度的一半；同时考虑到叶片前缘的特点和构造方便，令椭圆的另一条切线BC平行于X轴，切线BC距X轴的距离为c。设直线AC，AB的斜率分别为k1，k2，且k2≠-k1，那么直线AB，AC，BC直线方程可以分别表示为：

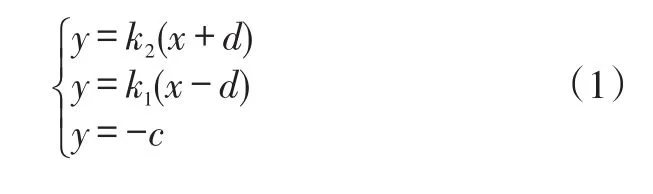
求 解 式（1）可 得 极 点A，B，C的 坐 标 为，若设椭圆的第三个切点K的坐标为(x1,-c)，G，F分别为极线PK和QK的中点，则中线AO1，BG，CF的方程可表示为：

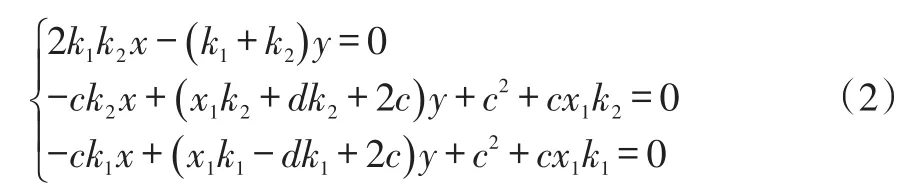
由椭圆的极点-极线性质可知AO1，BG，CF三条直线有共同交点O，求解式（2）可得椭圆中心O(x0，y0)的坐标为同时可得K点的横坐标，即K点为直线AO1的延长线与直线BC的交点，利用该性质可以快速得到求解椭圆所需三个点的坐标，这就是使直线BC平行于直线PQ的原因。

下面来求解椭圆的方程，由于椭圆中心O(x0，y0)坐标上面已求得，平面上任意位置的椭圆的方程[7]可以表示为：

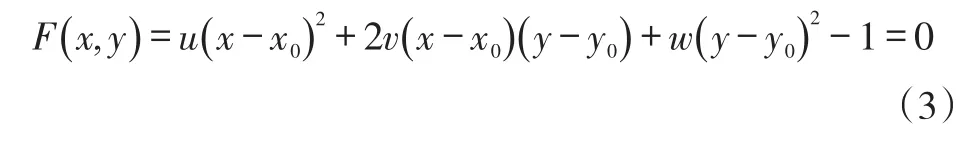
u，v，w为待定系数，将P，Q，K三点的坐标带入式（3）即可求出u，v，w三个变量，它们均为k1,k2,d,c四个参数的函数。将式（3）改写为一般二次曲线的形式：

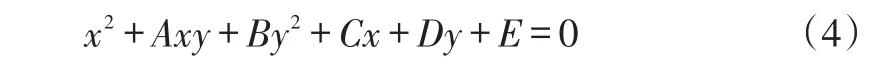
式中：

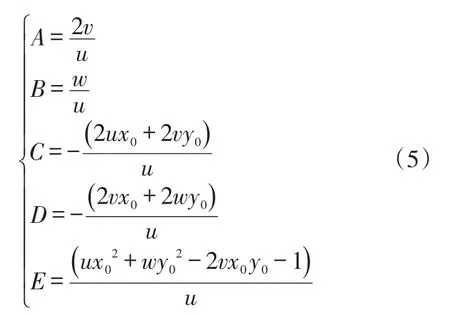
文献[8]给出了一般二次曲线的系数与椭圆特征参数之间的对应关系，其中本文只涉及到椭圆的长半轴a、短半轴b、长轴与x轴的夹角θ，即：

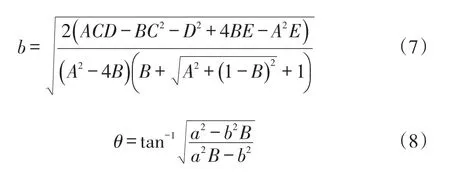
将式（5）代入式（6）、（7）可得椭圆长短轴的比例为：

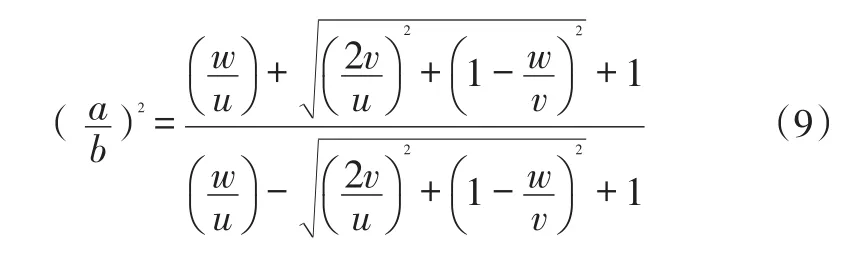
由于u，v，w均为参数k1，k2，d，c的函数，故椭圆长短轴的比例也仅取决于k1，k2，d，c四个参数。实际构造叶片前缘时k1，k2，d为已知参数，因此只需根据设计给定的椭圆长短轴比例式（8）求解参数c即可获得椭圆造型所需全部特征参数：椭圆中心坐标（x0，y0），长短轴半径a，短轴半径b，长轴与x轴的夹角θ。

从上面构造椭圆弧的方法可以看出，由于将椭圆的第三条切线选取在与叶片曲线前缘两端点的连线方向上，为椭圆弧的设计带来了极大的方便。此时的椭圆弧除了保证与叶片曲线前缘两端点相切外，仅需给定椭圆的长短轴的比例即可确定椭圆的形状与大小，方法简单，便于工程应用。

3　算例验证

本节通过两组数值算例验证前面所讨论算法的正确性，即检验反求出满足一定长短轴比例的椭圆是否与已知直线AB，AC切于点P，Q。在MATLAB软件中进行编程求解，思路为首先输入k1，k2，d，长短轴比例四个参数，利用公式（9）首先求出c的值，再通过P，Q，K三个点的坐标求出平面任意椭圆方程的参数u，v，w，最后表示出椭圆的5个特征参数：椭圆中心坐标（x0，y0），长短轴半径a，短轴半径b，长轴与x轴的夹角θ。

当k1=-5，k2=8，d=2时，得到长短轴比例分别为4:1，3:1的相切椭圆特征参数如表1所示；同样计算当-k1=k2=4.949 6，d=1.25时，与之相切的长短轴比例分别为4:1、3:1的椭圆特征参数如表2所示。对表1，2的数据进行绘图处理得到对应图3和图4，从下图可验证所求出椭圆均切于两条相交直线的特定点P，Q，因此证明上述推导理论的正确性，所以该方法可用来求解非扭转叶片前缘的椭圆方程。

表1　-k1≠k2时不同长短轴比例椭圆弧参数Tab.1　The parameters of the elliptical arc with different axial ratio of ellipse when-k1≠k2

表2　-k1=k2时不同长短轴比例椭圆弧参数Tab.2　The parameters of the elliptical arc with different axial ratio of ellipse when-k1=k2

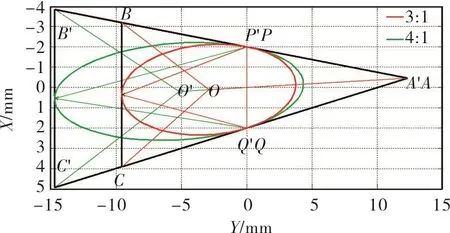
图3　-k1≠k2时椭圆长短轴比例分别为4:1，3:1Fig.3　Axial ratio of ellipse as 4:1,3:1 when-k1≠k2

图4　-k1=k2时椭圆长短轴比例分别为4:1，3:1Fig.4　Axial ratio of ellipse as 4:1,3:1 when-k1=k2

4　结论

针对非扭转叶片的椭圆形前缘构造问题，在深入研究椭圆极点-极线性质的基础上，提出了一种与叶片压力面和吸力面光滑连接的椭圆形前缘构造方法。该方法能保证所构造的椭圆弧与叶片压力面和吸力面上叶片曲线两端点相切，通过将椭圆的第三条切线选取在与叶片曲线前缘两端点的连线方向上，使得椭圆的形状仅取决于第三条切线的位置；进而利用椭圆的一般方程与椭圆特征参数间的对应关系，获得了影响椭圆形状的唯一设计参数，即椭圆的长短轴的比例。该方法原理简单、计算量小，在保证椭圆形前缘与吸力面和压力面一阶连续的同时，椭圆长短轴的比例还可以根据叶片气动性能的需要任意改变。