完全非弹性碰撞中的动能损失

董静雨

(石家庄市第二中学　河北 石家庄　050000)

2017年高考改革，将《物理·选修3-5》列为必考内容，在2018年高考中，与动量相关的知识也有很大可能成为高考热点．在动量守恒类问题中，碰撞问题，高考只要求一维情况，而在一维碰撞中，又可分为弹性碰撞、非弹性碰撞和完全非弹性碰撞3大类．其中，完全非弹性碰撞为重点问题，其特点是两物体碰撞后共速且有最大动能损失．

1　完全非弹性碰撞中的动能损失

在一般参考书中，对于完全非弹性碰撞的讨论仅限于碰撞过程中动量守恒

m1v1+m2v2=(m1+m2)v共

碰撞过程中动能损失最多

对于以上两个方程的解，并没有做过多的说明．

我们在平时做题过程中，会遇到大量的完全非弹性碰撞问题，对于大多数的题目都要求解以上两个方程．为此，我们不妨先求解以上两个方程的一般解的形式．

如果令

u=v1-v2

那么在碰撞过程中系统损失的动能为

通过求解发现，碰撞中损失的动能具有相当简洁的形式．对于这一结果，我们可以从如下角度讨论．

2　在质心系中探究动能损失

由于碰撞类问题常忽略外力作用，故在质心参考系中进行讨论是非常方便的．

根据柯尼希定理，质点系相对于基本参考系的动能等于质心动能和各质点相对于质心参考系的动能(简称相对动能)之和，有

式中M为质点系中各质点质量总和，vc为质心相对于基本参考系的速度，mi为各质点质量，vic为各质点相对于质心的速度．

一维两体碰撞问题中，设两质点质量分别为m1和m2，两质点相对于基本参考系的速度分别为v1和v2，两质点相对质心的速度分别为v1c和v2c．质点1相对于质点2的相对速度

u=v12=v1-v2=v1c-v2c

因为质心系为零动量参考系，即质心系中质点系的总动量必为零，故有

m1v1c+m2v2c=0

联立以上两方程解得

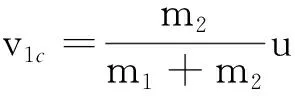
在质心系中，二质点相对于质心系的相对动能为

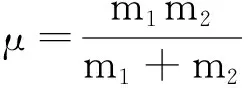
根据柯尼希定理，二质点系的动能可以写为质心动能与两质点在质心系的相对动能之和

3　实例分析

在清楚了完全非弹性碰撞中动能如何损失之后，对于高三复习中遇到的此类问题的求解将带来便利．碰撞中损失的动能可以转化为内能：如子弹打木块、板块；转化为势能：弹簧压缩到最短(拉伸到最长)，物块滑上光滑水平面上的非固定光滑斜面到最高点．

【例1】如图1所示，在光滑的水平面上有一质量为M的长木板，以速度v0向右做匀速直线运动，将质量为m的小铁块轻轻放在木板上的A点，这时小铁块相对地面速度为零，小铁块相对木板向左滑动．由于小铁块和木板间有摩擦，最后它们之间相对静止，已知它们之间的动摩擦因数为μ，问：在全过程中有多少机械能转化为内能？

解析：小铁块放到长木板上后，由于它们之间有摩擦，小铁块做加速运动，长木板做减速运动，最后

达到共同速度，一起匀速运动．过程中小铁块和长木板动量守恒，最终为共速状态，故该过程可等效为完全非弹性碰撞，因此全过程所产生的内能为损失的全部相对动能为

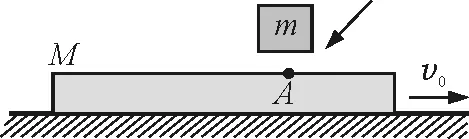
图1　例1题图

【例2】如图2所示，质量为M的滑块静止在光滑的水平面上，滑块的光滑弧面底部与水平面相切，一质量为m的小球以速度v0向滑块滚来，设小球不能越过滑块，求小球滑到的最大高度？

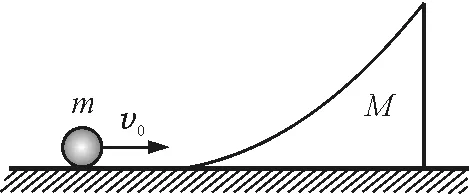
图2　例2题图

由此求得小球上升的最大高度为

以上关于完全非弹性碰撞模型的分析，从高中物理水平上升到普物水平，有助于师生从理论角度对完全非弹性碰撞过程中能量的损失与转化的把握，从而在实际解题过程中迅速解决问题．

参 考 文 献

1舒幼生. 力学(物理类). 北京： 北京大学出版社，2005. 152～153

2程稼夫.力学篇.合肥：中国科学技术大学，2013.197～198