自适应低空机动目标角跟踪算法*

鲁鹏威，贾方秀，王晓鸣，刘 铭

（1.南京理工大学智能弹药技术国防重点学科实验室，南京 210094；2.西安交通大学人居环境与建筑工程学院，西安 710049）

0 引言

在现代战争中，大量的空中机动目标出现在战场，并且以其高机动性、高灵活性、全天候作战和有效的攻击火力，承担着越来越重要的作用，使战争由平面发展到立体空间，对战略战术和军队组成等产生了重大影响。但是，随着地面雷达和低空导弹的日益完善以及反空火力的增强，空中机动目标在作战中的危险性不断增加。由于雷达对低空目标的快速反应能力很差、波束宽等原因，基于雷达体制的防空系统将无法完成对低空、超低空目标的探测与跟踪［1］。依靠地形地物的遮蔽和地面杂波的干扰，在低空飞行的目标不易被发现，所以低空和超低空突防成为空中单位的主要作战方式。

目前，在轻型防空武器系统超低空防空领域，仅有角测量的条件下，国内外学者提出了大量角跟踪算法。王勇等人［2］提出了“当前”统计模型下的扩展卡尔曼角跟踪算法，实现了目标的角跟踪，但是跟踪精度不高；Al-Emadi等人［3］提出了一种利用同步信号参考与振荡信号的角度跟踪技术的测量转换器，表现出优异的跟踪性能，但是所利用的系统较为复杂；任波等人［4］提出了非线性预测滤波算法，在选取恰当的加权矩阵条件下，可以实现有效的跟踪，但是，加权矩阵很难解析求到，主要根据经验给定，不能保证最优结果。本文针对轻型防低空武器系统，以低空机动目标为研究对象，分析其飞行轨迹，提出了一种基于角度的自适应跟踪算法，通过仿真证明了该算法的有效性和优越性，并且可以在简单的系统中实现。

1 算法设计

空中作战单位在低空或者超低空飞行时，一般采用地形跟随飞行方式，利用地物作掩护，在贴近地面的高度上隐蔽接近攻击目标［5］。低空机动目标的飞行特性主要分为机动飞行和非机动飞行。非机动飞行主要表现为巡航飞行；机动飞行包括以下的飞行方式：悬停跳跃、平飞加速、定常爬升、定常转弯、减速转弯、蛇形飞行和高速拉起等。

本文设计的低空机动目标自适应角跟踪算法的基本思路如图1所示。首先根据低空机动目标的飞行特性，建立合适的模型；然后根据建立的模型对滤波进行初始化设计；在初始化设计后，进行扩展卡尔曼滤波计算；滤波结束后进行模型的自适应修正，以提高接下来跟踪的精度；最后是滤波结果的输出。

1.1 建立目标模型

模型的设计对估计精度有很大的影响，在该算法中，将低空机动目标看作质点，观测用的传感器在坐标原点，具体的几何关系如图2所示。

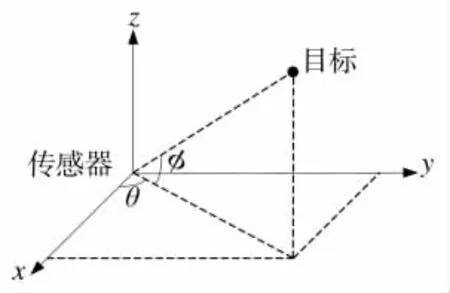
图2 目标与观测量的几何关系图

根据图2，建立如下的随机非线性系统：

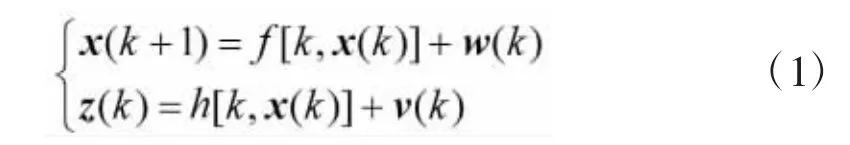
式中，f和 h 都是非线性方程；w（k）是以 Q（k）为协方差矩阵的系统过程噪声，v（k）是量测噪声，其协方差矩阵是 R（k）；x（k）是系统的状态向量，z（k）是系统的观测向量，具体关系如下：

综合之前的低空机动目标的飞行特性，建立“当前”统计模型，连续系统模型的描述如下［6］：

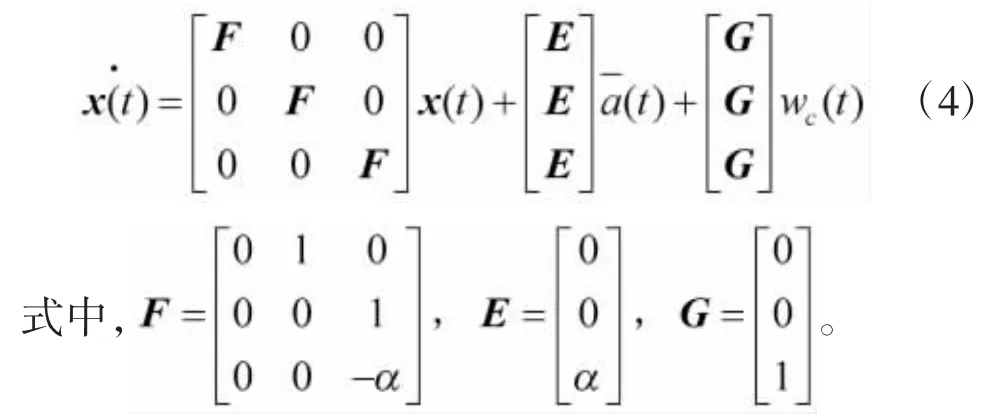
将“当前”统计模型离散化，得到离散形式的动力学模型如下：

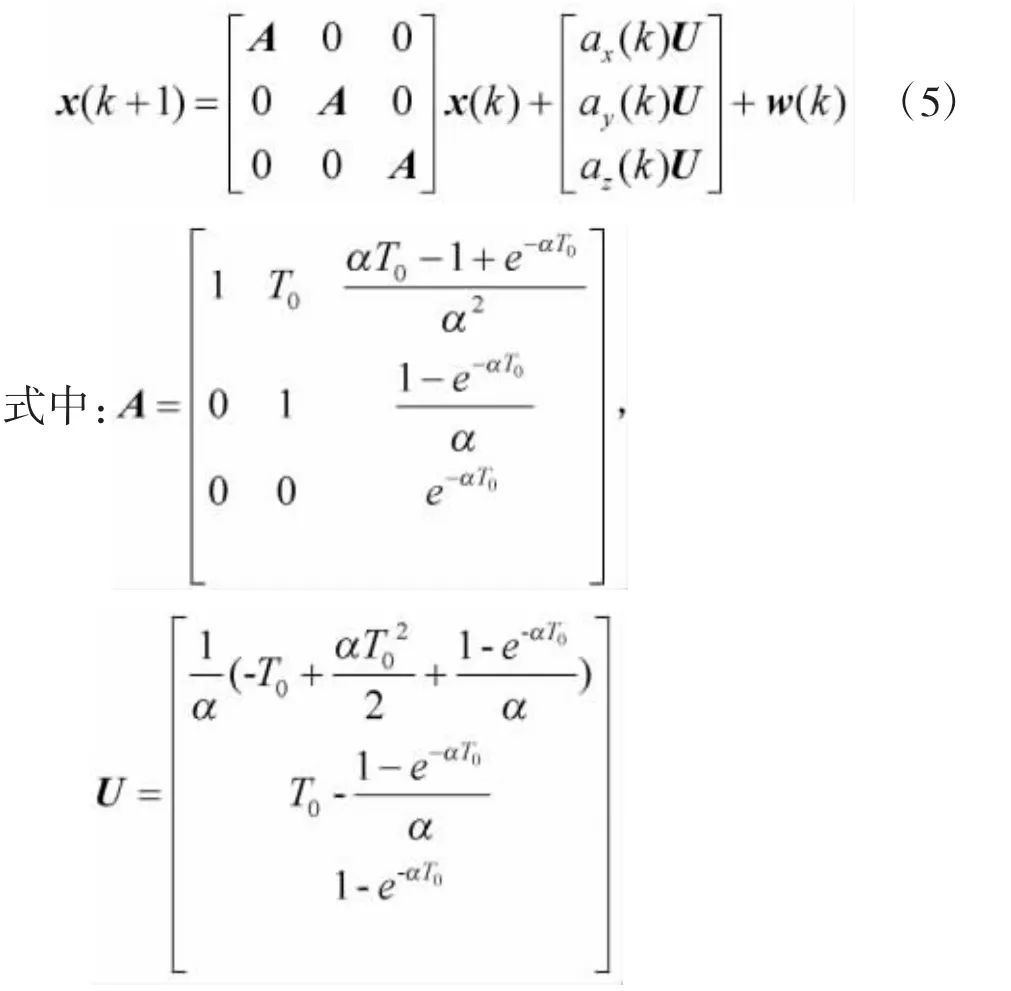
过程噪声方差Q的表示如下：

式中，aM与a-M是目标在某一方向所能达到的最大正加速度和最大负加速度，a是目前加速度的预测值。

1.2 扩展卡尔曼滤波

1.2.1 计算预测均值和方差

根据前文建立的模型，由于系统的非线性，采用扩展卡尔曼滤波进行状态估计［7］。首先计算飞行目标的预测均值和方差，计算公式如下：

心理距离四个维度之间的联系是潜在的自动化，与此同时，它们还具有相似性的特征。例如Pronin和 Olivola (2008) 证实了人们在对自己或者对他人进行未来决策时存在相似，但对现在的自己做决策则不同，这表明尽管分属不同距离维度，时间距离和社会距离存在一定的相似性。[29]Boroditsky (2000) 的研究同样证明，人们能够使用空间维度上的部分结构化信息用于处理时间问题，这说明时间距离和空间距离同样具有相似性关联。[30]此外，这四个维度还存在相互影响的联系，时间、空间和社会距离之间是相互影响的，当其中一种距离维度发生改变后，其他两种距离维度也将随之产生相应的变化。

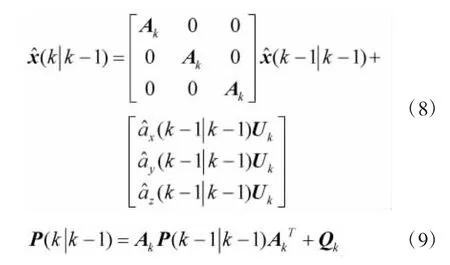
1.2.2 计算雅克比矩阵

1.2.3 计算观测预测、协方差矩阵和滤波增益

观测预测的计算如下：

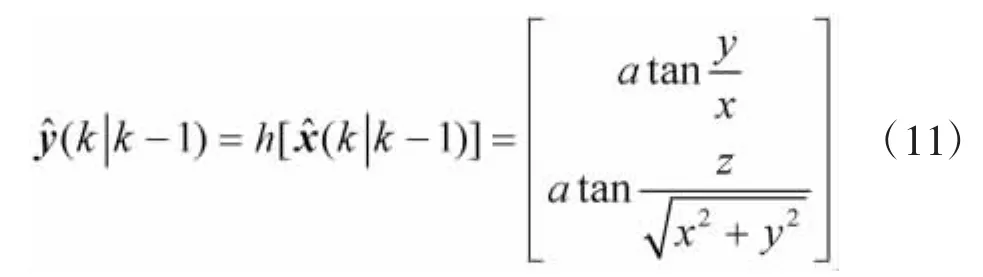
新息协方差矩阵计算如下：

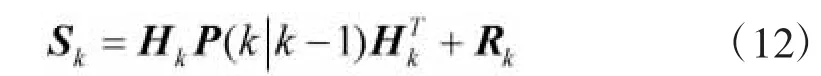
卡尔曼滤波增益计算如下：

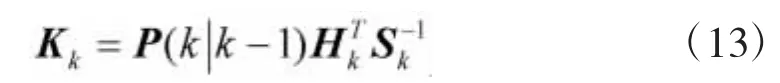
后验均值计算如下：

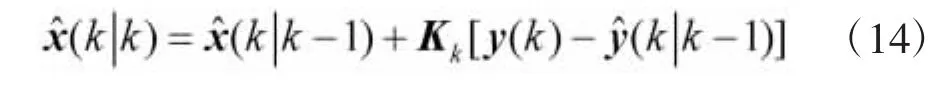
协方差矩阵计算如下：

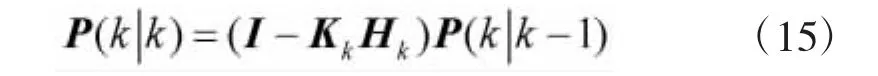
1.3 机动频率自适应

在“当前”统计模型中，机动频率α是根据跟踪目标机动程度来确定的，机动频率越小，目标的机动程度越大。低空机动目标可以进行机动性小的巡航飞行，也能够实现机动性强的飞行，所以，在该模型中，对机动频率进行自适应调整将会提高跟踪精度。

最小均方（LMS）算法具有计算简单、易于收敛等特性，可以很好地应用在实时性要求高的跟踪算法中，所以利用LMS算法对机动频率进行自适应调整［8］。

在LMS算法中，它的更新方程如下：

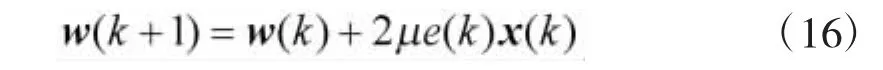
式中，μ是收敛因子，e（k）是预期输出与实际输出之差，x（k）是系统的输入，为了保证算法的收敛性，μ应该在一定的范围内取值。

将LMS算法应用到本文的扩展卡尔曼滤波中，将整个滤波系统看作一个网络，机动频率α就是这个网络的权值，e（k）x（k）是观测预测与实际观测之差，即，所以，可以得到机动频率α的调整公式：

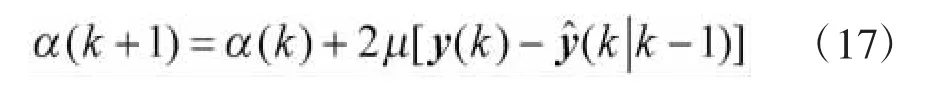
2 仿真与分析

考虑低空机动目标的飞行特性，利用计算机生成飞行轨迹，仿真的轨迹特征见表1，目标的飞行轨迹见图3，图中每个点之间的时间为0.1 s。然后计算出目标的高低角和方位角，作为理论数据，将观测误差以正态分布随机加到理论数据上，作为观测数据。本次仿真的采样时间为0.1 s，观测方位角和高低角的误差方差为1°，方位角理论值和观测值见图4，高低角理论值和观测值见图5。

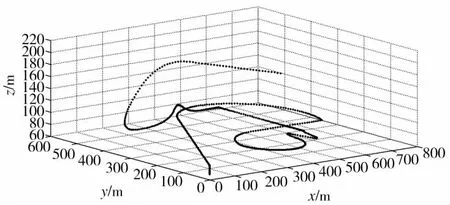
图3 飞行轨迹图

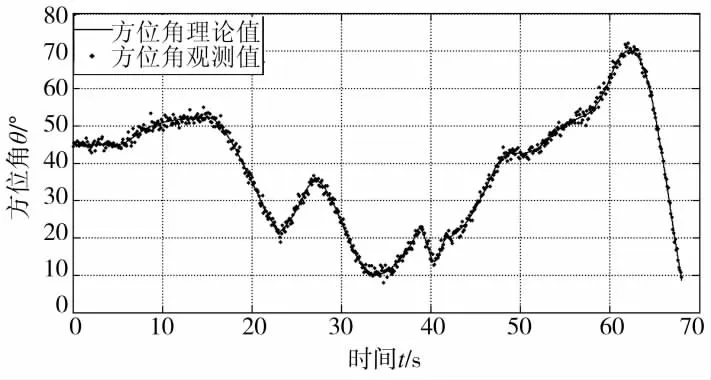
图4 方位角理论值和观测值

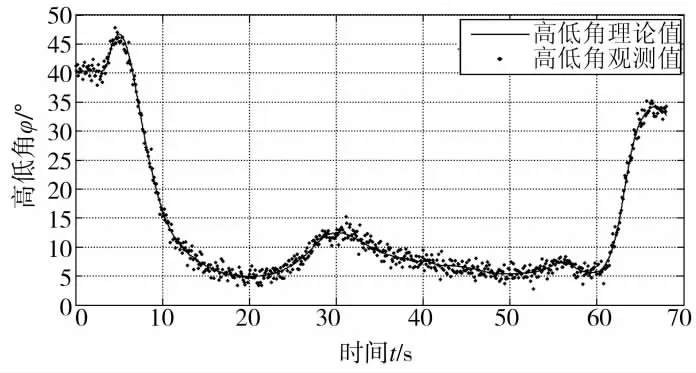
图5 高低角理论值和观测值

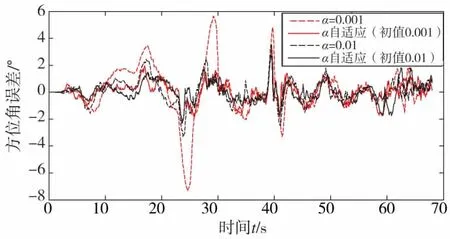
图6 方位角误差图

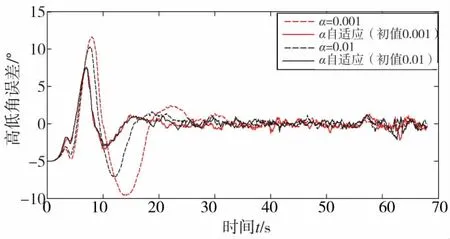
图7 高低角误差图

在进行仿真时，对固定的机动频率和自适应机动频率分别进行仿真，固定的机动频率取值为0.001和0.01，自适应机动频率的初始取值与其相同，方位角的误差见图6，高低角的误差见图7，计算整个过程的平均均方根误差见下页表2。

从方位角误差图和高低角误差图可以看出，机动频率自适应的角跟踪算法的误差明显小于单一机动频率的角跟踪算法。固定机动频率角跟踪中，当α取值为0.01时，误差总体上比α取值0.001时小；而在自适应机动频率角跟踪算法中，在经过一定的自适应步长后，不同初值对误差的大小影响不大。另外，在目标飞行状态改变较大的时候，固定机动频率的误差明显增大，而自适应机动频率的误差也有所增大，但是误差比固定机动频率的角跟踪算法要小。

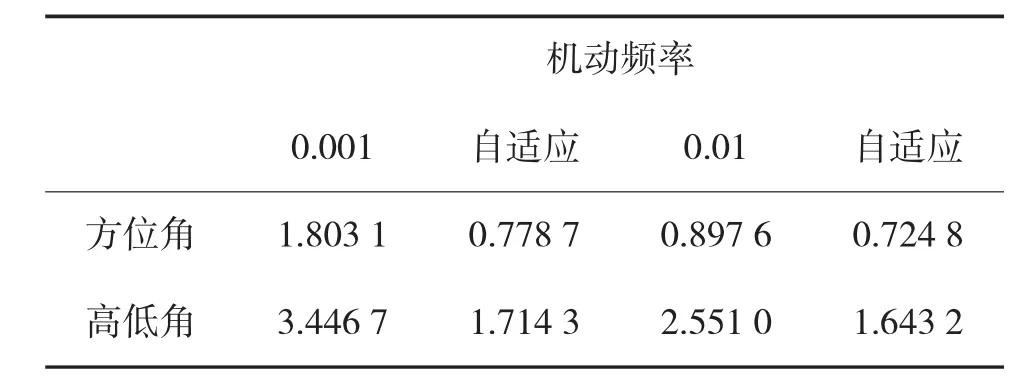
表2 几种角跟踪的平均均方根误差

通过几次仿真可以看出，自适应角跟踪算法的跟踪精度比传统的角跟踪算法的跟踪精度要高，并且初值的选取对跟踪精度的影响不大，都会把误差控制在一个很小的范围内。

3 结论

本文分析了低空机动目标的飞行特征，针对轻型防低空武器系统，设计了自适应角跟踪算法，并且详细阐述了算法的实现过程。对该算法进行仿真对比分析后，证明了该角跟踪算法的优越性，有良好的跟踪精度，同时具有计算速度快、稳定性好等优点。