ISG混合动力汽车模型预测控制能量管理策略*

徐赛培，宋 璐，付主木⋆，宋书中

（1.河南科技大学信息工程学院，河南 洛阳 471023；2.河南科技大学电气工程学院，河南 洛阳 471023）

0 引言

随着汽车保有量的逐年增加，使交通安全、环境和能源等问题日益严重。由于混合动力汽车兼具较低的排放性和良好的燃油经济性，使之成为近年来国内外的研究热点。模型预测控制是在滚动时域内反复优化控制序列来预测未来系统的行为，在受约束的多变量系统中有实现高性能的能力［1-2］，已有不少学者将模型预测控制应用在混合动力汽车的控制中，结合模型预测控制的优点进一步提高了混合动力系统的燃油经济性［3-5］。

混合动力汽车的能量管理控制策略需要解决的根本问题是在满足驾驶员对整车需求转矩的基础上，最优的分配发动机、电机系统的转矩输出［6-8］。Borhan等［9］提出利用需求转矩指数衰减的数学模型预测未来需求转矩值，将非线性模型近似为一个分段线性函数，利用二次规划算法对目标函数进行求解；Johannes等［10］提出利用模型预测控制方法设计一个级联控制器，预测车辆的短期负荷高峰和反复加载周期，有效地降低了燃油消耗；赵韩等［11］基于随机模型预测控制算法对并联混合动力汽车的转矩分配问题进行了研究，取得了良好的节油效果；孟凡博等［12］建立了发动机的动态模型，从混合动力汽车实际行驶的道路数据中提取和建立马尔可夫链，有效地提高了混合动力汽车的燃油经济性；罗禹贡等［13］针对混合动力汽车巡航过程的跟踪安全性和燃油经济性的优化问题，提出了基于非线性模型预测理论的混合动力汽车预测巡航控制策略。目前国内外在混合动力汽车能量管理方面取得的许多研究成果中，大多仅限于混合动力系统本身的研究，把驾驶员行为考虑在内的控制策略尚不多见。

文中针对ISG混合动力汽车，采用马尔可夫链预测车辆需求功率，对求得的需求功率模型结合驾驶员行为进行随机学习控制，将模型预测控制与动态规划算法相结合，通过优化得到混合动力汽车的转矩分配策略，使燃油消耗最小化。

1 ISG混合动力系统模型

文中所研究的ISG混合动力汽车整车动力系统结构如图1所示，ISG装在与发动机输出轴相连的两个离合器中间，发动机、电机功率可直接输出，电机功率还可作为辅助功率输出。

汽车动力学方程如下：

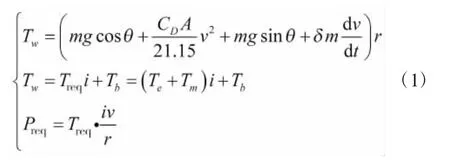
式中，Tw为车轮需求转矩，m为汽车的整备质量，CD为风阻系数，A为迎风面积，δ为旋转质量换算系数，θ为坡道角度，r为车轮半径，v为车速，i为传动比，Treq为动力源需求转矩，Te为发动机转矩，Tm为电机转矩，Tb为制动力矩，Preq为驾驶员需求功率。

2 驾驶员需求功率的随机学习模型

2.1 基于马尔可夫链的驾驶员模型

在车辆实际行驶过程中，将整车的需求功率视为具有马尔可夫性质的随机过程，其转移概率通过统计标准循环工况下的需求功率来获得。

首先将需求功率离散化为有限个实数值：

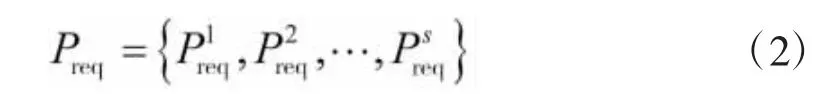
则在k时刻驾驶员需求功率为Preqi条件下，在k+1时刻驾驶员需求功率为Preqj的转移概率为：

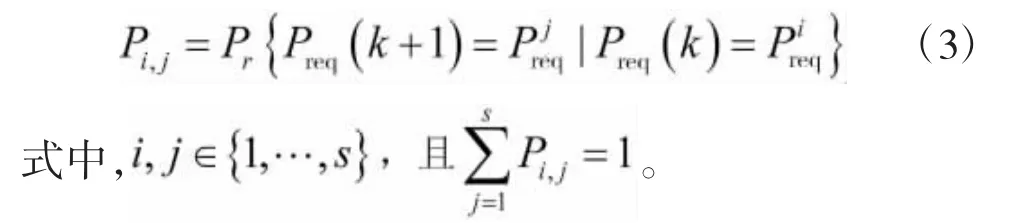
2.2 驾驶员模型的随机学习

车辆的动力学模型可以从物理和对象参数中得出，驾驶员的随机模型也可以从数据中识别。转移矩阵P中转移概率的值由最大似然法确定：

式中，i，j∈{1，…，s}，mi，j表示需求功率从 Preqi转移到Preqj的次数，mi表示需求功率从Preqj转移的次数之和：

把驾驶员自身状态、驾驶环境等一些影响驾驶行为的随机变量定义为驾驶员行为。式（3）从批处理数据中确定了转移概率矩阵，但是随着时间的变化，驾驶员行为也会发生变化，所以马尔可夫链需要通过递归算法进行更新。使δi∈{0，1}s定义转移的发生，因此，转移矩阵P可以递推地表示为：

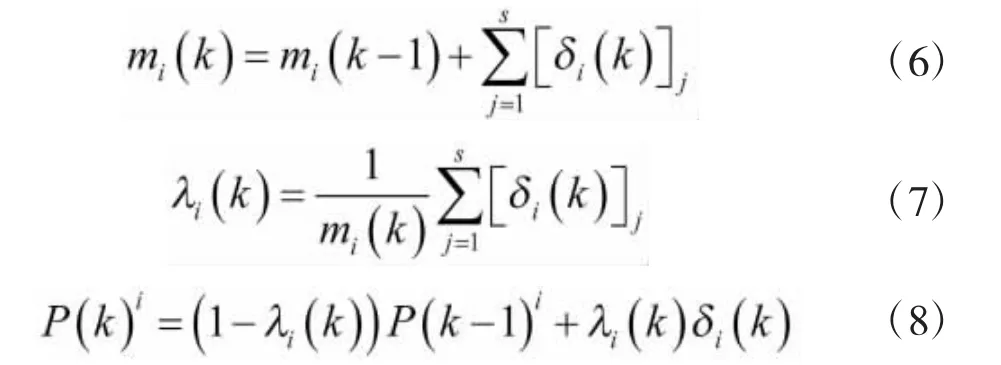
式（6）更新了需求功率从Preqi转移的次数之和，式（7）储存了从每个状态转移的总数，式（8）更新了转移矩阵。实际上，在每个时刻，转移矩阵P只有一行更新。

由于式（6）～式（8）对新数据的敏感度随数据量增加而减少，如果驾驶员行为固定的将不会影响计算，但是在实际的驾驶中，由于受交通状况、路况和驾驶员自身的状态等因素影响，驾驶员的行为也会受到影响。为了克服这些限制，保持数据的灵敏度不变，式（6）和式（7）由式（9）代替：

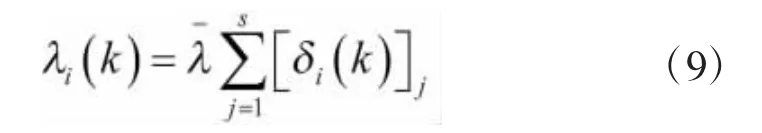
3 模型预测控制能量管理策略

电机/发动机的转矩分配是ISG混合动力汽车优化能量管理的基本控制问题，优化目标包括燃油消耗和电池SOC的平衡。转矩分配的前提为需求转矩是发动机转矩和电机转矩之和，预测区间内的总需求转矩可通过需求功率求取，因而电机/发动机的转矩两者确定一者即可。因此，文中选取电机转矩为控制变量，电池SOC为状态变量。

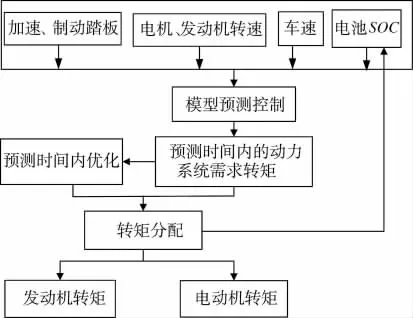
图2 模型预测控制流程图

3.1 模型预测控制的具体步骤

模型预测控制的具体步骤如下：

1）通过传感器得到当前k时刻的车速、电机、发动机转速等信号，通过估算得到系统的当前状态。

2）预测接下来时间p内车辆的需求功率，每隔周期k预测一次，由驾驶员需求功率的随机模型得到未来p时间的功率需求预测序列，并根据式（1）计算出时间p内对应的动力源的需求转矩、转速和车速。

3）通过优化算法在［k，k+p］内进行优化，得到预测期内最佳的电机转矩序列，，以及相应的发动机转矩序列

4）将3）算出的最优转矩分配比序列中第1个时刻的电机转矩Tm（k+1）、发动机转矩Te（k+1）作为当前控制周期结束k+1时刻控制器输出的命令，发送给电机、发动机。

下一个控制循环，再依次执行1）～4），由k+1时刻车辆的状态得出k+2时刻最佳的电机、发动机转矩，反复执行上述步骤，即可得出每个控制时刻最佳的电机转矩和发动机转矩。

3.2 模型预测控制求解

动态规划算法适合求解有约束的非线性最优化问题，随机模型预测控制的学习算法中，在预测时间内计算转矩的分配，计算量已大幅减小，因此，文中采用动态规划算法求解有限时域内目标函数的最小值。

在总控制周期k至k+p内，目标函数可表示为：

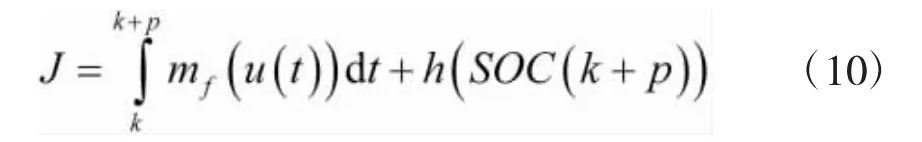
能量管理策略的目标是在满足动力学方程约束的条件下，最小化目标函数。但是在实际应用中，经过多个步长周期，车辆的模型参数和约束条件可能会有所不同，而且在优化过程中，每个控制周期的步长也要满足计算要求，因此，将上述最优控制问题转化为每个阶段最小燃油目标函数，可表示为：

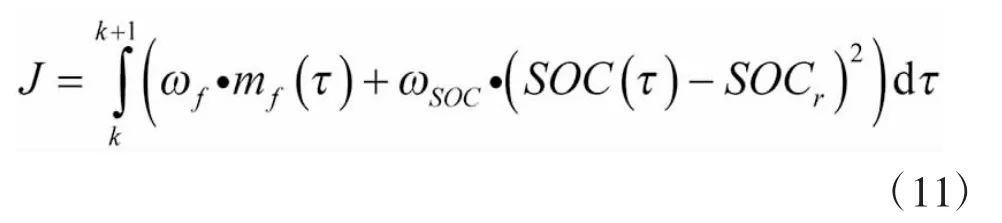
式中，mf为燃油消耗率，ωf＞0 和 ωSOC＞0 为相应权值，SOCr为期望的电池SOC参考值。

根据Bellman最优化原理，可将式（11）转化为：

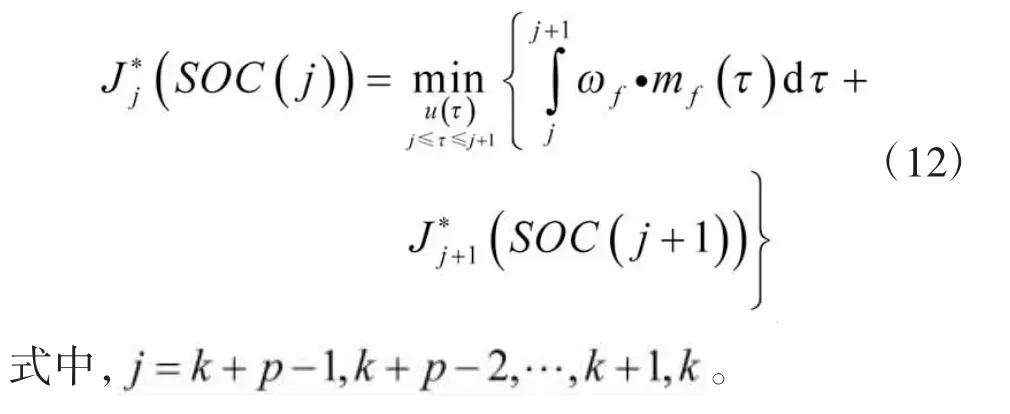
4 仿真分析

为验证所设计的ISG混合动力汽车的模型预测控制能量管理策略，在Matlab/Simulink和Advisor环境中的CYC_ECE_EUDC和CYC_REP05路况下进行仿真，电池SOC初值设置为0.7，表1为仿真所用的整车主要部件参数。所设计的随机模型预测控制能量管理策略仿真结果如图所示。

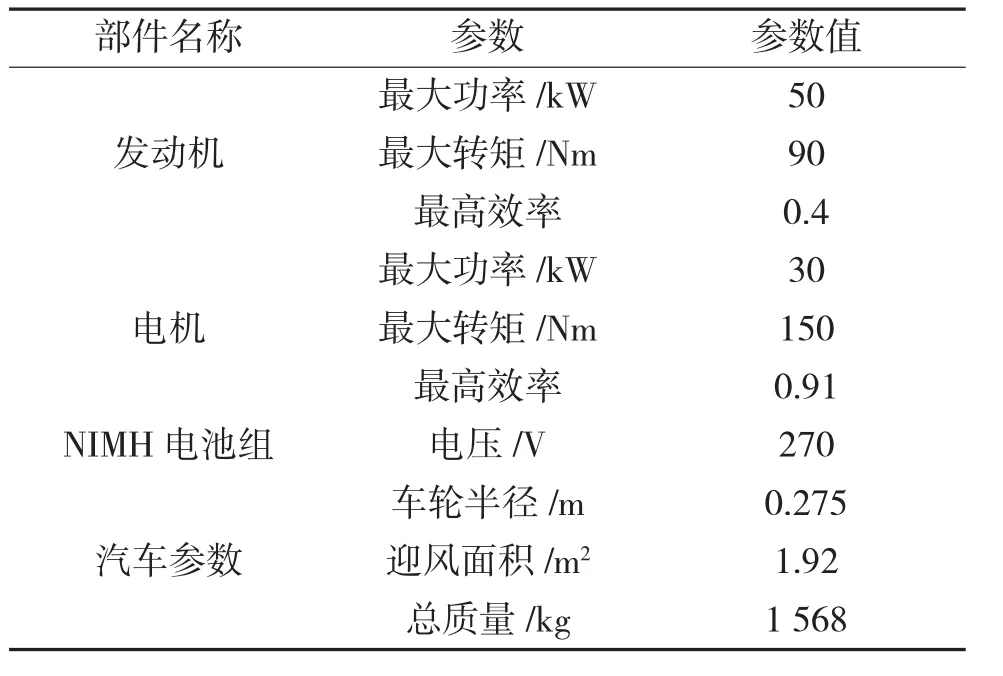
表1 整车主要部件参数

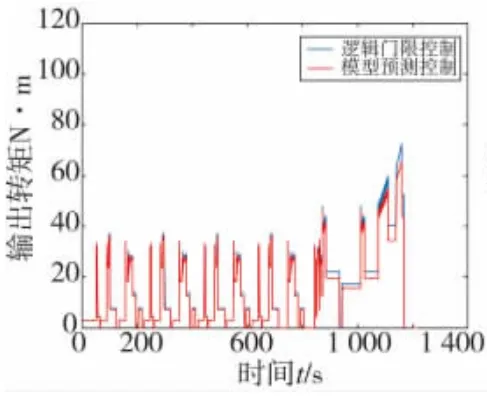
图3 EUDC工况下发动机转矩变化曲线

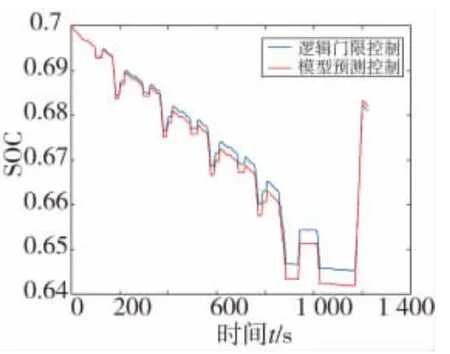
图4 EUDC工况下电池SOC变化曲线

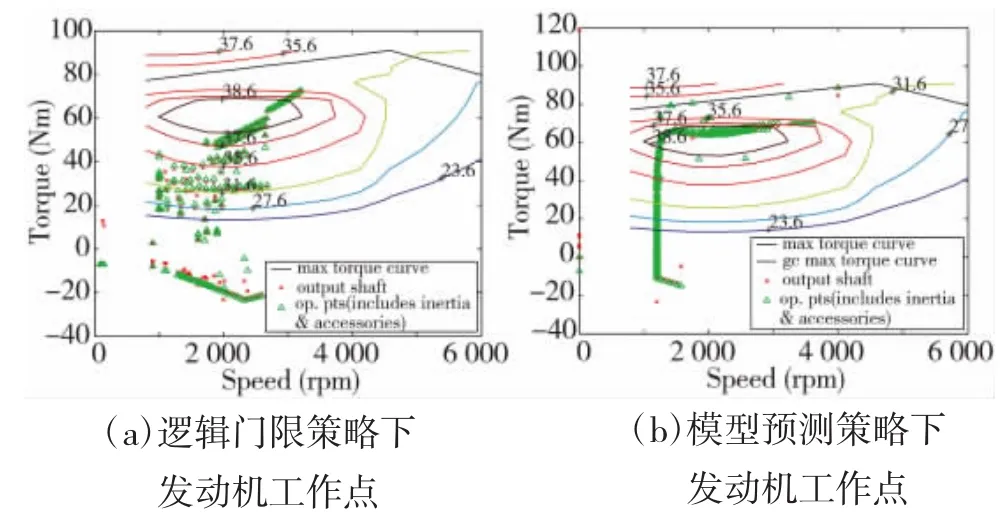
图5 EUDC工况下两种策略的发动机工作点分布

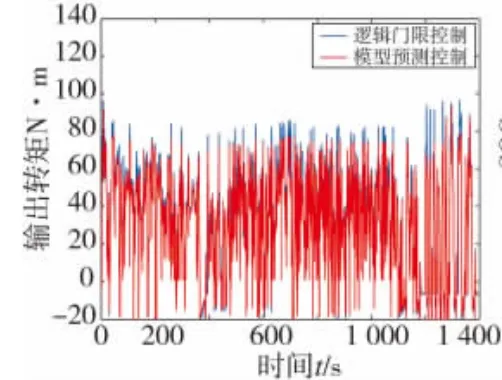
图6 REP05工况下发动机转矩变化曲线

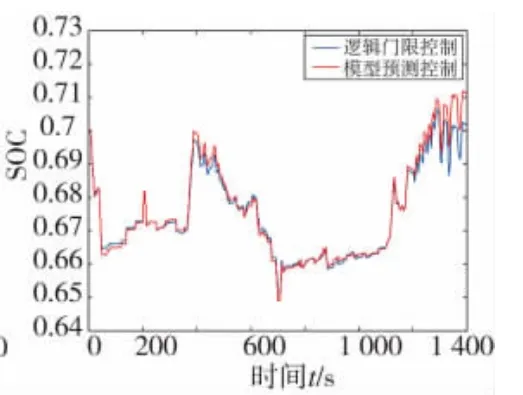
图7 REP05工况下电池SOC变化曲线

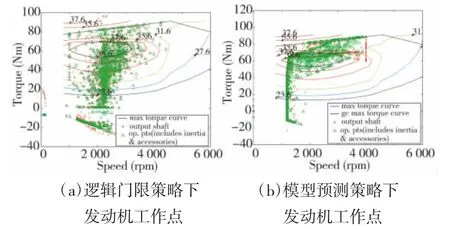
图8 REP05工况下两种策略的发动机工作点分布

由图3～图8可知，文中所设计的模型预测控制策略与逻辑门限相比，汽车在加速或者爬坡时，发动机转矩波动较小，大多数发动机工作点在高效区域内工作，发动机的工作效率明显提高，有利于节省燃油并降低排放，在两种行驶工况下，末端电池SOC有小幅提升，能更好地维持电池SOC平衡。

模型预测控制与逻辑门限控制策略相比，在CYC_ECE_EUDC道路循环下，燃油经济性从60.6 mile/gal到64.5 mile/gal，提高了6.5%。在CYC_REP05道路循环下，燃油经济性从63.4 mile/gal到67.3 mile/gal，提高了6.2%。

5 结论

文中提出了一种对驾驶员需求功率随机模型学习的方法，在求得驾驶员功率需求的马尔可夫链模型后，对驾驶员行为进行随机学习，使系统对驾驶员习惯和不同交通状况的变化进行调整。动态规划算法结合模型预测控制以燃油消耗最小化为目标进行滚动优化，在Advisor和Matlab/Simulink平台上搭建仿真模型，基于驾驶员需求功率随机模型学习能够更准确的预测汽车的动力需求，与逻辑门限控制策略相比，该控制策略能够有效改善ISG混合动力汽车的燃油经济性。