基于最小资源损耗的火力分配研究

刘志超，石章松，姜 涛，刘志坤

（海军工程大学，武汉 430000）

0 引言

传统的火力目标分配往往是以联合毁伤概率最大［1-4］或所有来袭目标总期望生存值最小为模型［5］进行的一次分配，这种情况造成了火力资源的浪费，在单批来袭目标数目少，来袭批次多的情况下无法进行持续抗击。文献［6］在联合毁伤概率最大的基础上，提出使所用的火力单元总量最小作为第2个目标函数，采用一种改进的多目标粒子群优化算法进行求解，在与单目标函数对比中显示了一定的有效性，但在毁伤概率最大和消耗火力单元总量最小这两个相斥的目标上需要合适的效费比指标进行方案选择。武器目标分配实质是一个整数型非线性组合优化问题［7］，求解方法多种多样，目前解决武器目标分配的算法大致可分为以整数规划法、动态规划法、启发式搜索法等为代表的传统算法，以禁忌搜索算法、遗传算法、粒子群算法、蚁群算法和模拟退火算法等为代表的智能算法和将上述两种以上算法结合起来对武器目标分配进行求解的混合算法三大类［8］。

现代战争中，为了实现最大军事效益，饱和攻击模式由传统的一次性将尽可能多的弹药投向敌方平台转变为利用敌方平台防御间隙进行少量多批次的打击。为在有限资源约束下抗击更多批次来袭目标，本文在满足抗击毁伤概率指标P和武器弹药资源约束的前提下，建立最小资源损耗武器目标分配模型并采用粒子群禁忌混合搜索算法对问题进行求解。粒子群算法操作简单，全局寻优能力强，但运行到后期收敛速度较慢、求得的解精度不高，而禁忌搜索算法全局搜索能力弱、局部搜索能力强且收敛速度快，进行两种算法的结合可有效提高对模型最优解的搜索能力。

1 最小损耗武器目标分配数学模型

问题可描述为，同一批次来袭目标数小于空闲火力单元数时，假设每批空中来袭目标有m个，记为T1，T2，…，Tm，进入了 n 个空闲火力单元 W1，W2，…，Wn的防区，其资源数量分别为 Q1，Q2，…，Qn，每个火力单元只能同时打击一个目标，每个目标都遭到打击且可分配多个火力单元进行打击，令Xij表示决策变量，若分配第i个火力单元拦截第j个目标，则Xij=1，否则Xij=0，Pij表示第i个火力单元对第j个目标的毁伤概率，最小资源损耗武器目标分配模型如下

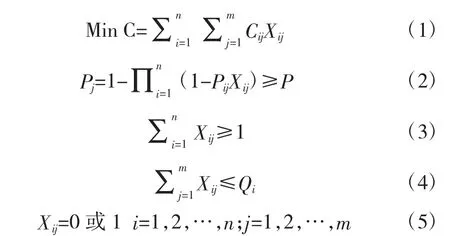
式中，Cij为资源价值，式（2）～ 式（4）表示在满足抗击毁伤概率指标P和武器弹药资源约束的前提下，每个来袭目标都能受到火力打击分配，式（2）中P可根据专家意见或弹药实际情况由指挥员进行设定。

2 求解最小损耗武器目标分配模型的禁忌搜索离散粒子群混合算法

2.1 离散粒子群优化算法

对粒子群算法的研究目前主要集中于连续型的粒子群算法，而任务分配是一个离散问题，为对其进行求解人们设计了离散粒子群算法并将其与其他算法结合，从而实现优势互补。在离散粒子群算法中，每个粒子都是一个备选解，最小资源损耗武器目标任务分配的关键在于确定哪个来袭目标由哪个或者哪几个火力单元进行抗击，每个粒子长度等于空闲火力单元数量n，粒子由按空闲火力单元编号顺序排列的目标编号组成，表示一种可能的分配方案，设空闲火力单元数量n等于5，目标数目m等于3，第l个粒子为

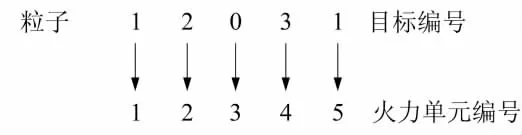
表示：火力单元1攻击来袭目标1；火力单元2攻击来袭目标2，火力单元3空闲，火力单元4攻击来袭目标3，火力单元5攻击来袭目标1。若某来袭目标未分配火力单元进行打击或对某来袭目标毁伤概率不满足毁伤概率指标P，则资源损耗设为无穷大，以此来筛选出符合约束条件的粒子。

粒子群算法的关键在于粒子，粒子通过对个体极值和全局极值的学习来更新自己的速度和位置信息，进而向最优解靠近，典型粒子速度和位置更新公式如下：

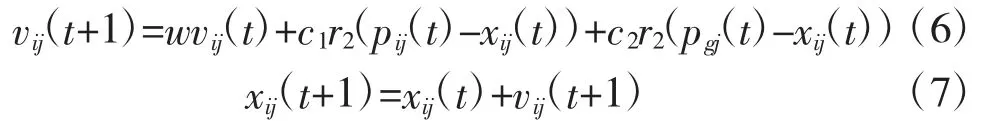
式（6）第1项是粒子对当前速度的继承，w为惯性权重，第2项表示粒子向自身经历过的最好点靠近，第3项表示粒子向群体中优秀个体或群体中的历史最优点靠近。C1，C2为学习因子，r1和 r2为［0，1］间的随机数，l=1，2，…M，M 为粒子数量，j=1，2，…，n，针对所研究问题的实际特点，对粒子群算法位置和速度更新公式重新定义如下

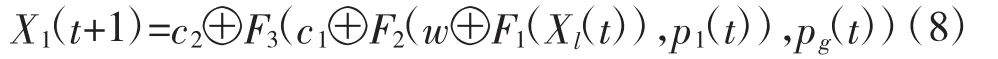
式中：X1=（xl1，xl2，…，xln）为粒子 l在迭代中的位置；pl=（pl1，pl2，…，pln）为粒子 l的个体极值；pg=（pg1，pg2，…，pgn）为全局极值；w，c1，c2均介于［0，1］之间。位置更新公式构成如下，设Ψl，Φl为临时变量。

这对应式（6）第1项，该式代表一个概率为w的粒子位置矢量的置换操作，rand（）＜w时，产生两个［1，n］上的随机数a和b，然后将粒子位置矢量的第a和第b个位置的数值进行互换操作，即第a个火力单元攻击的目标和第b个火力单元攻击的目标进行置换操作，rand（）＞w时Ψl（t）=Xl（t）。

这对应式（6）第2项，该式代表一个概率为的粒子位置矢量的交叉操作，若rand（）＜c1，产生两个［1，n］上的随机数a和b，然后将粒子位置矢量的第a至第b个位置的数值与个体极值pl相应位置的数值进行交叉操作，即将第a个火力单元攻击的目标至第b个火力单元攻击的目标与个体极值pl中第a个火力单元攻击的目标至第b个火力单元攻击的目标进行互换，rand（）≥c1时Φl（t）=Ψl（t），进行式（9）的计算。

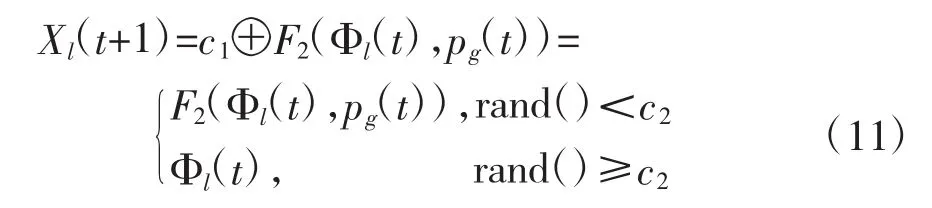
这对应式（6）第3项，该式代表一个概率为的粒子位置矢量的交叉操作，若rand（）＜c2，产生两个［1，n］上的随机数a和b，然后将粒子位置矢量的第a至第b个位置的数值与全局极值pg相应位置的数值进行交叉操作，即将第a个火力单元攻击的目标至第b个火力单元攻击的目标与全局极值pg中第a个火力单元攻击的目标至第b个火力单元攻击的目标进行互换，rand（）≥c2时Xl（t+1）=Φl（t），进行式（10）的计算，经过式（9）～式（11）不断迭代更新，最终的pg（t）即为全局最优解。

2.2 禁忌搜索离散粒子群优化算法

禁忌搜索算法是人工智能的一种成果，它可通过引入一个灵活的禁忌表存储结构和相应的禁忌准则来避免迂回搜索，并通过破禁策略来赦免一些被禁忌的优良状态，进而保证多样化的有效搜索以最终实现全局优化。它对初始解要求较高，好的初始解会有效提高收敛速度和搜索到的最优解质量，其主要思想为给定一个初始解和利用邻域函数选定若干候选解，若候选解适应度优于当前最优解，则替代当前最优解并按照规则进行禁忌表更新，若候选解中不存在优于当前最优解的解，则在候选解中选出最优状态的解作为当前解并按照规则进行禁忌表更新，重复迭代过程，直到满足预设停止规则。

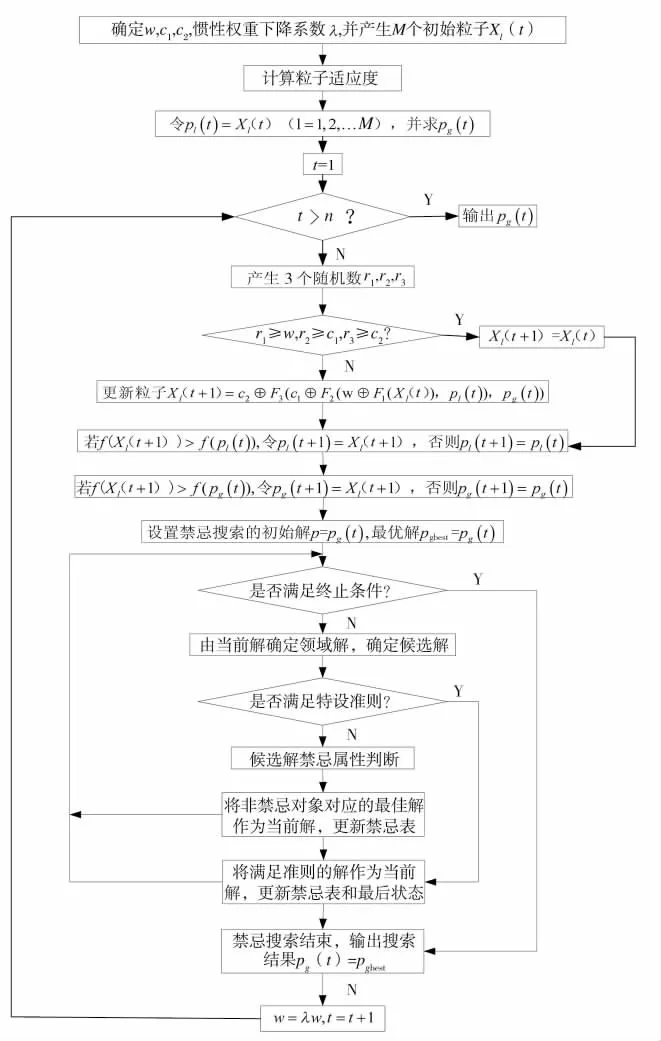
图1 粒子群禁忌混合搜索算法流程图

本文中禁忌搜索离散粒子群算法是在每次迭代中离散粒子群算法给出的全局极值pg（t）的基础上，使其任意两个火力单元对应的位置为0作为候选解集，直接进行禁忌搜索，若某粒子优于当前最优解pg（t），则忽视其禁忌状态对当前全局极值pg（t）更新操作，若没有改进，使其任意一个火力单元对应位置为0作为候选解进行禁忌搜索，若某粒子优于当前最优解pg（t），则忽视其禁忌状态对当前全局极值pg（t）更新操作，若没有改进，结束禁忌搜索并判断是否满足结束条件，不满足时进行新一轮的循环，粒子群禁忌混合搜索算法流程图如图1所示。

3 仿真实验

假设某时刻某海上防空平台空闲火力单元有8个 W1，W2，…，Wg，某批空中目标 T1，T2，T3，T4同时来袭，空闲火力单元资源价值Ci如表1所示，武器对目标杀伤概率如表2所示。

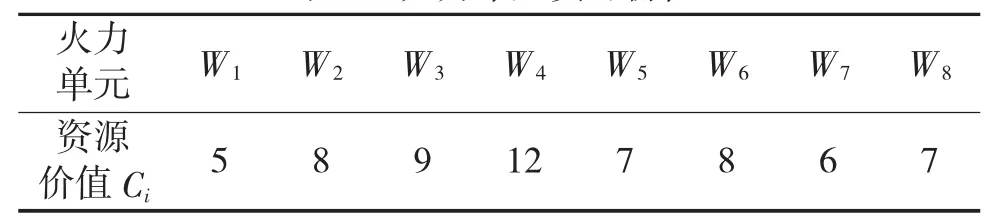
表1 火力单元资源价值

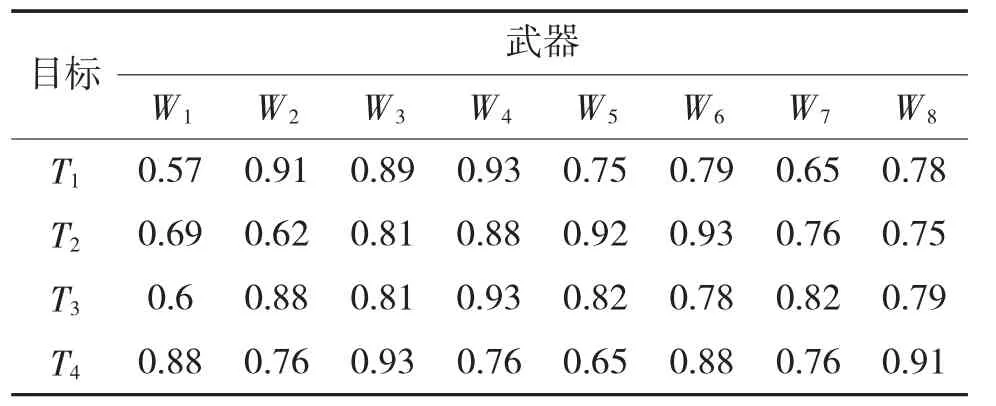
表2 武器对目标杀伤概率

分别采用粒子群算法和粒子群禁忌搜索算法对实验进行仿真计算。仿真参数设置如下：粒子数取50，惯性系数w初始设置为0.9，线性下降至0.4，c1取值0.8，c2取值0.8，两种算法各迭代100次，重复循环30次，对比在不同要求毁伤概率P下，每次循环中得出的资源消耗最小值和平均值大小。毁伤概率P分别取值0.8，0.9，如图2～图5所示。

从一次抗击资源总消耗来看，在要求毁伤概率P=0.8和P=0.9的情况下，粒子群禁忌混合搜索算法和粒子群算法最优值分别为 26（4，1，0，0，2，0，3，0）和 33（3，1，0，0，2，0，3，4），但从每次循环平均值看，粒子群禁忌混合搜索算法性能明显优于粒子群算法，每100次迭代得到最优解的可能性更加稳定。

4 结论

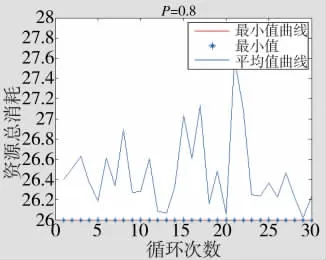
图2 粒子群禁忌混合搜索算法

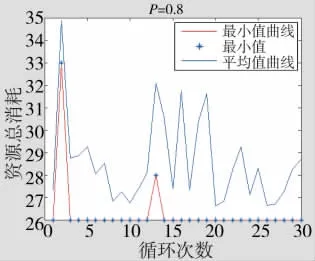
图3 粒子群算法

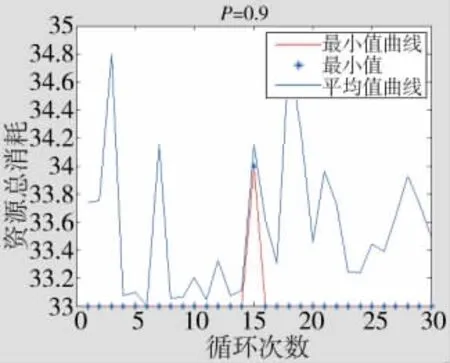
图4 粒子群禁忌混合搜索算法

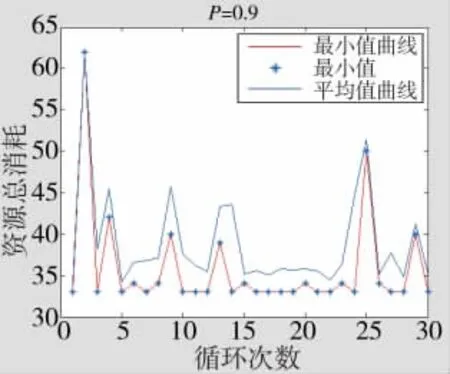
图5 粒子群算法

为充分利用火力资源，解决传统火力分配中目标存活概率最小或对目标毁伤概率最大存在的资源浪费情况，本文提出了在满足抗击毁伤概率指标P和武器弹药资源约束前提下的最小资源损耗武器目标分配模型，由指挥员根据同一批次来袭目标威胁度和火力资源的剩余情况合理设定毁伤概率，在火力资源充足的情况下可将毁伤概率指标P均设置在同一较高标准上，在火力资源不足的情况下可根据来袭目标威胁度分别设置其毁伤概率指标P，避免过饱和打击中的火力资源浪费，并通过算法改进，采用粒子群禁忌混合搜索算法对问题进行求解，仿真结果表明，相对于粒子群算法，粒子群禁忌混合搜索算法得出的解质量更高，相同迭代次数中得出最优解的性能更加稳定。