基于贝叶斯网络的汽车制动系统可靠性分析*

陈琳 谢学飞

（南通职业大学）

随着人们对汽车行驶安全性的重视，对汽车制动系统进行可靠性分析显得尤为重要。然而，汽车制动系统存在很多不确定因素，这给汽车制动系统可靠性分析带来了一定的困难[1]。文献[2]将故障树分析法应用到汽车制动系统中，找出了系统薄弱环节。然而，故障树分析法计算比较繁琐，不能进行多态分析。相比于故障树分析法，贝叶斯网络是一种处理不确定性知识和进行概率推理的重要工具[3-4]，文献[5]利用贝叶斯网络对汽车液压制动系统进行了分析，验证了该方法的有效性。但是，以上的分析结果都是建立在事件的精确概率基础上的。现如今，系统部件的失效概率以及事件之间的逻辑关系很难表达，呈现出模糊性，因此，文章提出一种利用模糊贝叶斯网络对汽车制动系统进行可靠性分析的方法，更好地解决了复杂系统的可靠性和安全性问题。

1 汽车制动系统贝叶斯网络的建立

汽车气压制动系统主要由制动踏板机构、制动阀、制动管路及制动器等组成。当制动踏板自由行程不符合要求、制动管路泄漏、制动器间隙不当或有关零部件受到损坏时，就会发生制动失效、制动不灵、制动跑偏、制动拖滞及制动噪声等故障[6]。汽车制动系统故障发生的原因比较多，且故障发生形式表现出多态性，又因为系统各部件发生故障的统计数据很难获得，所以有必要采用改进的可靠性分析方法对汽车制动系统进行分析。贝叶斯网络是一种处理不确定性知识和进行概率推理的重要工具，是关于概率关系的有向图解描述，它能够结合观测的数据信息和专家知识，具有描述事件多态性和信号逻辑关系非确定性的能力，现已经逐渐应用于可靠性分析领域。

文章首先根据汽车气压制动系统的使用情况及发生故障的部件，以制动功能失常为顶事件，由上到下，逐步找出所有导致制动功能失常的原因，建立贝叶斯网络模型，如图1所示。

图1 汽车气压制动系统的贝叶斯网络模型

2 贝叶斯网络的多态节点描述及概率值确定

2.1 贝叶斯网络的多状态节点描述

在对复杂系统进行可靠性分析时，一般是把研究对象看作是二态的，所谓二态性是指系统及其部件只有“正常”和“失效”2种状态[7]。但是，实际上很多系统及其部件表现出来的不仅仅只有2种状态，从“正常”到“失效”中间往往还包含着多种工作状态，比如，汽车制动系统中的制动阀，它不仅包括正常和漏气2种状态，还存在部分漏气的状态。所以说仅考虑二态就过于简单了，而且会存在很大误差。相比故障树，贝叶斯网络在分析能力上更具有优势，它具有多态逻辑表达能力，因此文章采用贝叶斯网络对系统进行可靠性分析，在考虑“正常”和“失效”2种状态的基础上，考虑“部分失效”状态，并用 0，1，2 分别表示“正常”“部分失效”“失效”3 种状态[8]。

2.2 模糊贝叶斯网络节点概率值的确定

针对数据缺乏、贝叶斯网络先验概率难以获得的问题，文章采用模糊理论与贝叶斯网络结合的方法来对汽车制动系统进行故障诊断。在用模糊贝叶斯网络进行分析时，最关键的是得到模糊先验概率，并通过解模糊化得到精确值。

2.2.1 建立评判等级

模糊数反映了人们对模糊概念或模糊信息的认识，强调了人在系统可靠性分析与评价中的重要性[9-10]。由于线性的隶属函数具有运算简便的特点，故文章采用三角模糊数来描述事件的失效概率。模糊数的获得通过专家打分法得到，为了将专家对事件发生概率的评判结果与模糊数联系起来，又因为汽车制动系统各部件发生故障的概率比较小，引入“非常高”“高”“偏高”“中等”“偏低”“低”“非常低”7个语言变量，为便于计算，将三角模糊数统一用 F=（a，b，c）进行表示，如：事件发生概率偏低，模糊数为（0.1，0.3，0.5）。

2.2.2 专家打分

为了更准确地利用模糊数来量化事件失效概率，有必要邀请多位专家对各个事件进行打分，综合各个专家的评判结果。各个专家的基本信息，如表1所示。

表1 各个专家基本信息

根据表1中的信息，利用层次分析法[11]得到各个专家的权重，用Wj表示，j为专家序号：W1=0.122 9，W2=0.428 4，W3=0.393 2，W4=0.139 5。

根据建立起来的评判集，设计基本因素专家打分表，邀请专家进行打分，为了结果的准确性，需要结合部分原始数据进行多轮打分，从而形成最终分析结果，经过计算得到综合模糊失效率，如表2所示。

表2 各个根节点综合模糊失效率

2.2.3 去模糊化

模糊化指把精确的量转换为模糊集的过程，更有利于模糊推理，但是在利用贝叶斯网络计算叶节点概率以及各根节点后验概率时必须要先得到各根节点的精确概率值，所以需要对模糊失效概率进行去模糊。去模糊化的方法有很多种[12]，例如：极右最大法、均值面积法及重心法等。由于均值面积法计算比较简单，文章采用均值面积法将模糊失效概率转化为精确失效概率，如表3所示。

表3 各根节点精确失效概率值

2.3 模糊贝叶斯网络条件概率的获得

同样，贝叶斯网络中的条件概率（CPT）值也要进行调整。CPT值是用来表示节点间的逻辑关系的，通过指定每个节点的CPT值来描述此节点在其父节点的所有取值组合下处于不同故障状态的条件概率。为方便得到CPT值，将传统逻辑门转换为T-S门，再将T-S模糊故障树转换为相应的贝叶斯网络，只需用T-S门规则给贝叶斯网络对应节点的CPT赋值就可以了。由文献[11]的定义可知，多态逻辑门的T-S规则：在多状态系统中或门的输出事件的状态为所有输入部件状态中最坏的部件状态；而与门的输出事件的状态为所有输入部件状态中最好的部件状态。

2.4 贝叶斯网络的概率计算

对汽车气压制动系统的贝叶斯网络模型各节点概率进行赋值后，可以实现预测、诊断、分析及优化设计等功能。在计算贝叶斯网络节点概率值的时候，贝叶斯网络比较复杂，特别是对系统进行多态分析时，计算量较大。因此必须选用贝叶斯网络工具箱（BNT）对其进行计算，进行可靠性评估[13]。基于M ATLAB的BNT是一个很灵活的工具，只需进行编程就可计算出所有节点的概率值，叶节点（T）处于不同状态的概率：p（T=0）=0.255 983，p（T=1）=0.364 301，p（T=2）=0.379 716，由叶节点概率P（T=i）的值可知该汽车制动系统的可靠性不高，部分失效和失效概率均超过35%。

由BNT还可以求出各根节点的后验概率，如表4所示。通过后验概率，比较它们的数值大小，可以找出对顶事件发生影响最大的基本事件，找出系统的薄弱环节。这是故障树法所不具有的优势。由各基本事件的后验概率可以对汽车气压制动系统进行故障诊断，诊断推理是由结论推知原因，在明确故障模式的情况下，推理故障原因。若故障已发生，在维修的同时，可以排除故障源，提高可靠性；如故障未发生，推理可以给汽车气压制动系统的优化设计提供资料，根据原因大小次序，对薄弱环节加以强化。后验概率越大，对气压制动系统制动失常的影响也就越大。由于文章的贝叶斯网络CPT值是由T-S门规则调整得来的，因此表4中的P（Xi=2|T=1）=0，也就是说，当系统部分故障时，各部件完全故障的可能性为0。

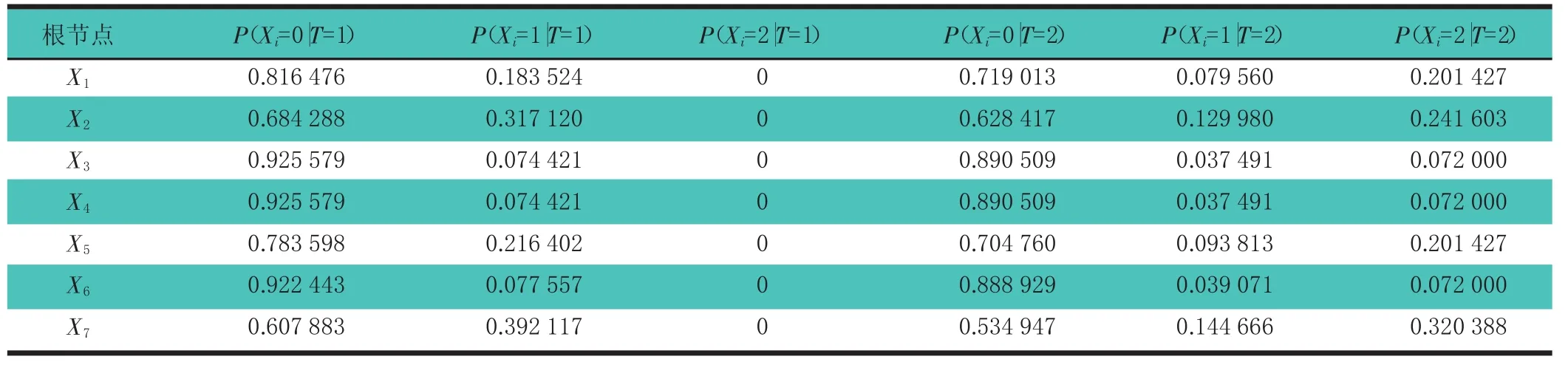
表4 各基本事件的后验概率

由表4可知，当T处于1状态，也就是系统部分故障时，检测到完好的各根节点概率排序如下：X3=X4＞X6＞X1＞X5＞X2＞X7，发生部分故障的根节点概率排序为：X7＞X2＞X5＞X1＞X6＞X3=X4。可以发现 2 种情况下，概率排序正好是相反的，这与实际情况相符。而且通过概率排序，发现X7为系统发生部分故障时的最薄弱环节，制动系统执行机构失常最能导致整个系统发生故障，而整个系统发生故障后又会引起其他一系列部件受损，因此设计人员可以对此进行优化设计，减少故障发生率，从而提高整个气压制动系统的可靠性。

当T处于2状态，系统发生严重故障时，检测到完好的各根节点的概率排序为：X3=X4＞X6＞X1＞X5＞X2＞X7；发生部分故障的根节点的概率排序为：X7＞X2＞X5＞X1＞X6＞X3=X4；发生严重故障的根节点排序为：X7＞X2＞X5=X1＞X6＞X3=X4。当系统发生故障时，可以按照以上顺序对故障原因进行一一排除。同时，综合分析3个概率排序，可得X7为该汽车气压制动系统的最薄弱环节。

3 结论

1）文章将模糊理论引入多态汽车制动系统的故障分析中，拓宽了贝叶斯网络解决不确定性问题的适用范围，相比于二态而言，考虑到了不同故障状态对汽车制动系统的影响，分析结果更符合实际，具有较强的工程实用价值。

2）该方法利用模糊数描述部件的多种故障状态，采用模糊子集描述部件的模糊故障率，运用贝叶斯网络的条件概率表描述部件间的故障逻辑联系，解决了部件间联系的不确定性。

3）将模糊贝叶斯网络应用于汽车制动系统的故障诊断中，仅是一个初步探索，还有待进一步改进，特别是条件概率的取值，文章只是利用T-S规则进行了调整，可以尝试其他方法获得更准确的概率值。