几类电力控制数为1的平方图

赵　敏,陈　琴

(中国计量大学 理学院,浙江 杭州 310018)

1　简　介

近三十多年来,图的控制数理论已成为图论的一个重要研究领域,在相关学科领域具有广泛的应用.根据不同的应用背景,人们定义并研究了多种控制参数[1-9].关于图的控制理论的全面研究进展可参看文献[8,9].2002年,Haynes等在文[10]中首先研究了电力网的监控问题.电力公司为了实现对整个电力网运行的监控,需要在电力网中选择一些电力节点来放置监控设备(PMU).由于PMU成本的昂贵性,我们希望在保证整个电力网被完全监控的前提下,选择尽可能少的节点放置PMU.如果电力网中所有的电力节点和电力传输线都能被放置在电力网中的PMU所监控,那么就称整个电力网被这些PMU监控.Haynes等把这类电力网的监控问题转化到图论上,发现它与图论中经典的点覆盖及控制集问题有着密切的关系.

用G=(V,E)代表整个电力网,G的顶点代表电力节点,边代表连接两个电力节点的传输线.一个PMU监控它所在的电力节点及与此节点关联的边和这些边的另一个端点(这些节点和边称为被监控).其它被监控的规则如下:

1)如果一条边被监控,则与它关联的点也被监控;

2)如果两个相邻的点被监控,则连接这两点的边也被监控;

3)如果一个点与k条边关联(k>1),并且这k条边中有k-1条被监控,则这k条边都被监控.我们称电力控制集具有“传递性”.

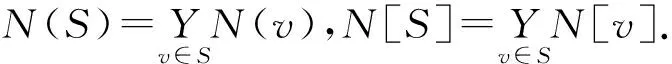
设S⊆V(G),若N[S]=V(G),则称S为图G的控制集.最小控制集的基数称为控制数,记为γ(G).基数恰为γ(G)的控制集称为G的γ(G)-集.若S为G的控制集,则称S控制图G.根据电力网中特定的“监控”规则,Hayne等[9]定义了电力控制集的概念.设S⊆V(G)是监控集,如果G的所有点和边都被监控,则称S为G的电力控制集,最小电力控制集的基数称为电力控制数,记为γP(G).基数恰为γP(G)的电力控制集称为G的γP(G)-集.若S为G的电力控制集,则称S电力控制图G.文中其它未加定义的术语和记号可参看文献[8]和[9].

本文将研究平方图的电力控制集问题,给出几类电力控制数为1的平方图.

2　主要结果

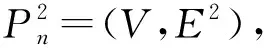
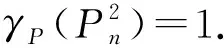
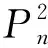
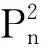
设圈

C

n

=(

V

,

E

),其中

V

={

v

1

,

v

2

,…,

v

n

},

E

={

v

i

v

i+1

|

i

=1,2,…,

n

}.则

其中

E

2

={

v

i

v

i+1

,

v

i

v

i+2

|

i

=1,2,…,

n

},这里点的下标取

n

的模.如图2所示.

图2　图

类似定理2.1,可以证明以下结果:

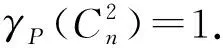
关于路与圈的k次方图的电力控制数,我们有下列结果:

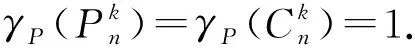
下面我们讨论平方格子图的电力控制数.图P2□Pn与P3□Pn的平方图如图3.我们有下列结果:

定理2.4:设Pn是阶数为n≥2的路.那么γP((P2□Pn)2)=1.

证明:设D={(1,2)},则D监控N[(1,2)]={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3)}(图3(a)中黑色的点).对于N[(2,2)]={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(2,4)}中的点,除了点(2,4)外,其余点均被D监控,所以(2,4)也被D监控.同理,对每个i=1,2,j=3,4,…,n-2,N[(i,j)]中的点,除了点(i,j+2),其余点均被D监控,所以(i,j+2)也被D监控.因此,D是平方图(P2□Pn)2的电力控制集,即γP((P2□Pn)2)=1.

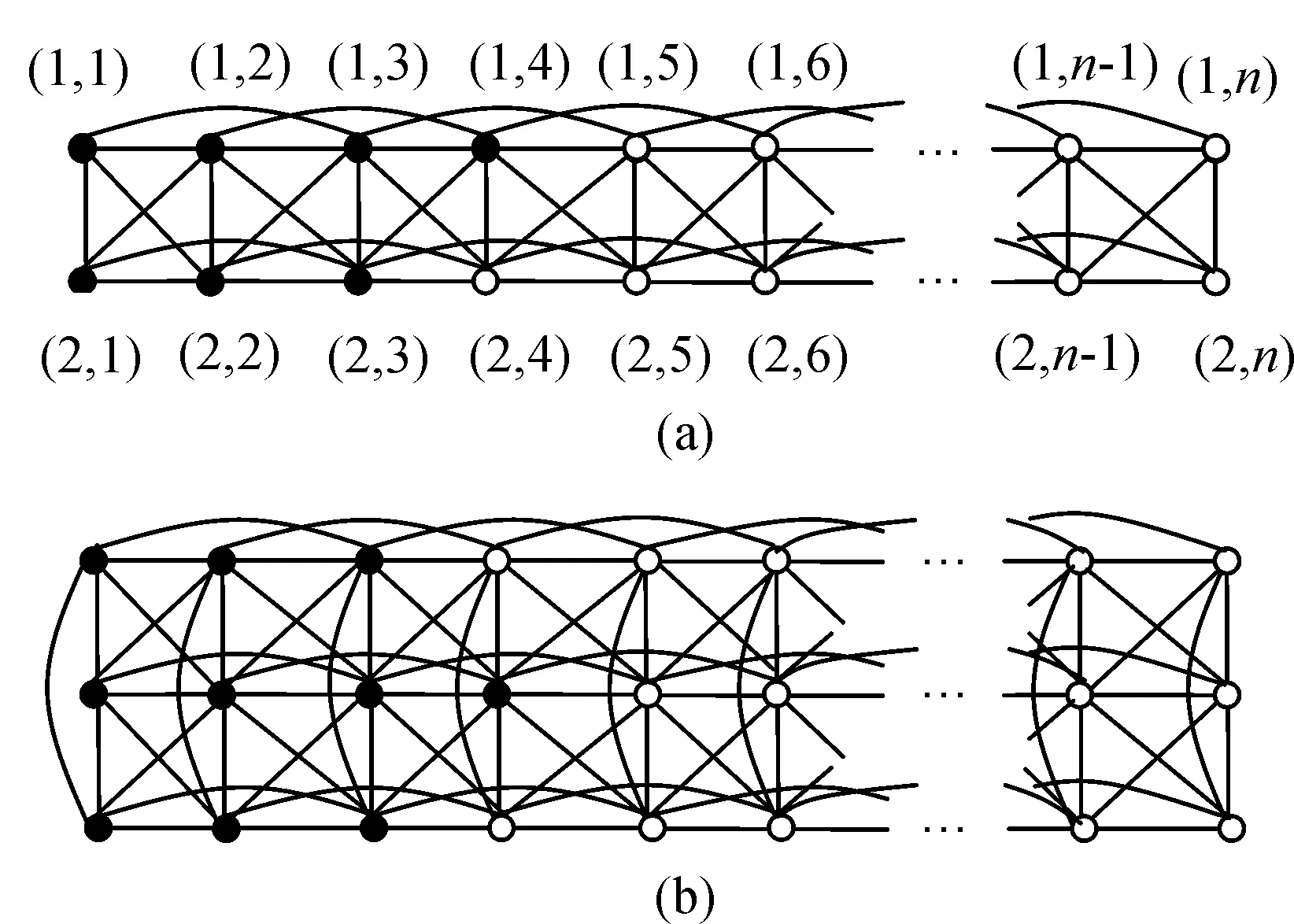
图3　P2□Pn与P3□Pn的平方图Figure 3　The square graphs of P2□Pn and P3□Pn

定理2.5:设Pn是阶数为n≥3的路.那么γP((P3□Pn)2)=1.

证明:设D={(2,2)},则D监控N[(2,2)]={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3)}(图3(b)中黑色的点)对于N[(1,2)]中的点,除了点(1,4)外,其余点均被D监控,所以(1,4)也被D监控.同理,对于N[(3,2)]中的点,除了点(3,4)外,其余点均被D监控,所以(3,4)也被D监控.依次考察i=2,1,3,对每个j=3,4,…,n-2,因为N[(i,j)]中的点,除了点(i,j+2),其余点均被D监控,所以(i,j+2)也被D监控.因此,D是平方图(P3□Pn)2的电力控制集,即γP((P3□Pn)2)=1.