基于分级规划策略的拟人机械臂仿人运动规划算法研究

王春荣，夏尔冬，赵 京，熊昌炯，刘建军，卫 沅



基于分级规划策略的拟人机械臂仿人运动规划算法研究

王春荣1，夏尔冬1，赵 京2，熊昌炯1，刘建军1，卫 沅3

(1. 三明学院机电工程学院，福建 三明 365004；2. 北京工业大学机械工程及应用电子技术学院，北京 100124；3. 河南科技大学车辆与交通工程学院，河南 洛阳 471003)

为使拟人机械臂具有高精度的仿人运动，提出一种通过触发条件和分级规划策略的仿人运动新方法。将人臂运动过程离散为不同运动阶段，在每一个运动阶段都有与之对应的规划层，在不同的规划层中，拟人机械臂的运动特点不同。利用各自的特点建立不同规划层下的运动模型及臂姿预测指标，对拟人机械臂臂姿进行预测。最后，以NAO机器人为实验平台，比较所提方法与最小势能法(MTPE)的静态臂姿与动态臂姿预测，并与运动捕捉系统(OptiTrack)采集的真实人臂运动数据进行比较。实验表明，该方法具有较小的静态臂姿和动态臂姿预测误差，能使拟人机械臂产生高度逼真的仿人运动。

拟人机械臂；仿人运动；分级规划策略；臂姿预测

人类作为自然界长期进化的高等生物，在结构和功能上有着许多独特的优越性，如人臂的安全性、柔顺性、运动灵活性等。把人体的相关特性融入并应用到机器人相关研究中，不仅可以使机器人的结构和功能产生质的飞跃，还可以帮助仿人机器人更好地融入人类社会生活并与人类进行高效、友好地沟通协作，甚至成为人类的伙伴[1-3]。对于拟人机械臂而言，只有与人相似的结构是不够的，更重要的是希望能够像人臂一样运动，具有与人臂相似的运动特性。因此，拟人机械臂的仿人运动规划就显得尤为重要。

臂姿预测作为拟人机械臂仿人运动规划的基础，一直以来都是仿人运动的重点及难点。臂姿预测方法的准确性对拟人臂仿人运动精度有着重要的影响。目前，关于拟人臂臂姿预测的方法主要包括静态预测和动态预测。在静态预测中，学者们主要将研究重点放在了运动过程中的某些特殊时刻(如开始、结束等)，采用基于指标或基于特性的方法来实现静态臂姿的预测，如YANG等[4]建立了一系列的指标，并用多目标优化方法来预测臂姿；KIM等[5]利用手臂的几何特性解决了逆运动学求解问题，并实现了臂姿的预测；ZHAO等[6]建立了一个虚拟扭簧模型，并利用多元统计回归方法解决了变弹簧系数，实现臂姿预测。在动态预测中，学者们主要对运动过程中手臂状态的变化进行研究[7]，不同的关节组合构成了丰富多彩的运动类型[8-10]。对于静态臂姿预测方法，无论是基于指标还是基于特性，都存在不可避免的缺陷。在基于指标的研究当中，单一指标往往不能够满足仿人运动的需要，而多指标体系由于权重系数的影响，又存在很多不确定性。在基于特性的研究中，尽管有很多方法能够提取人臂臂姿特性，但是其准确性还有待进一步的验证。对于动态臂姿预测方法，大部分的研究目的只是为了实现计算的简化，并未反映出人臂运动的内在机理。

因此，本文提出了一种分级规划策略，将完整的运动过程离散为不同的运动阶段，每一阶段都有与之对应的规划层，在不同的规划层中建立各个规划层中的运动模型和臂姿预测指标，并将其融入到拟人机械臂的仿人运动规划中，使拟人臂可以高度逼近人臂的真实运动。

1 拟人机械臂模型

本文采用由法国Aldebaran Robotics公司研制的仿人机器人NAO为实验平台。目前，在学术领域内，NAO是应用非常广泛的仿人机器人[11]。该机器人全身共有25个自由度，其中具有两个对称结构的5自由度拟人臂，每只手臂包括3自由度的肩关节、1自由度的肘关节及1自由度的腕关节。图1所示为NAO机器人手臂结构简图。利用DH参数法对其手臂进行运动学建模，DH参数见表1，其中1，2，3分别为NAO大臂、小臂及手部的长度。

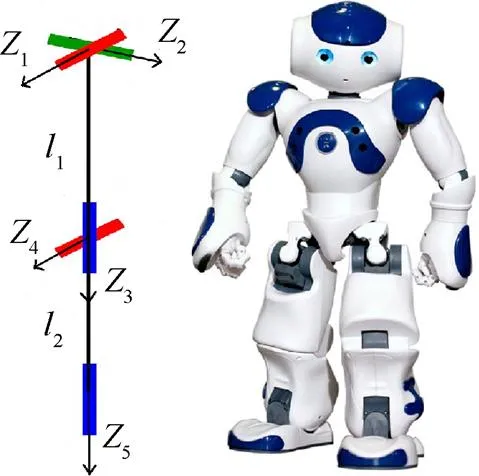
图1 NAO手臂坐标系

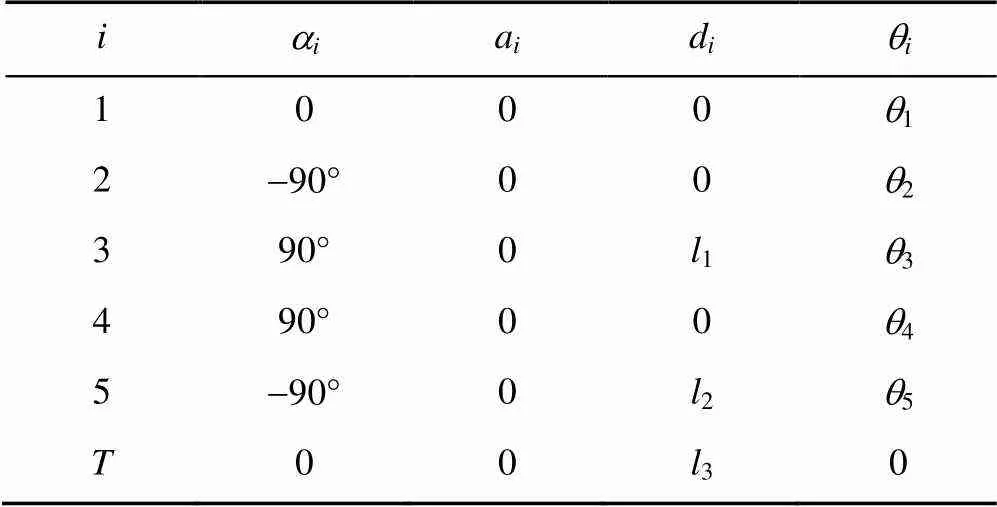
表1 NAO手臂的DH参数

目前，仿人运动实验大多采用运动捕捉技术来获取人体运动信息[12-13]，本文利用如图2所示的由NaturalPoint公司研制的OptiTrack全身运动捕捉系统来获取实验者们的手臂运动数据。该捕捉系统是一种高级光学动作捕捉系统，通过配备的8个Flex摄像头，可以准确地对穿着运动捕捉衣的实验者身体的关键部分进行动作捕捉，其自带的软件通过视觉系统识别和处理这些标志，具有很高的精度。

图2 运动捕捉系统

尽管NAO不具备人臂常用的7自由度配置，但是明确的生理关节配置使其依然广泛地应用到了仿人运动规划当中[14]。本文将通过运动捕捉系统采集到的人体运动数据转换为NAO配置下的运动数据，以避免不同个体人臂臂长的差异性影响，同时也可实现实验结果数据的统一表达。利用等比例缩放方法，将人臂臂姿转换为NAO的臂姿[15]。以肘关节为例，假设通过运动捕捉系统得到的人臂肘部在笛卡尔坐标下的位置为

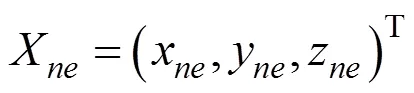
进一步求得人臂肘部在肩部的球坐标系下对应的坐标参数为

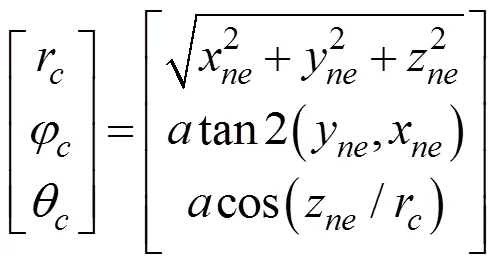
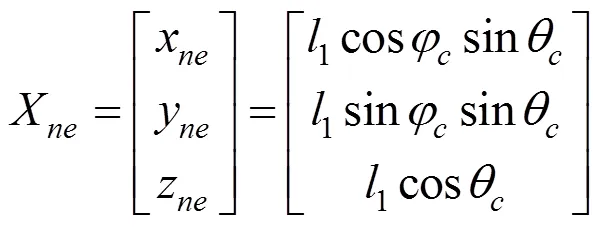
同理，可以得人臂腕部、手部在NAO关节配置中的具体位置，具体推导过程与意义详见文献[15]。通过该方法，使NAO的手臂运动能够符合人臂运动的特点。

2 分级规划策略

手臂的运动是复杂多样的，不同关节的协调组合形成了丰富多彩的运动类型。本文基于手臂运动的特点，提出了一种分级规划策略(hierarchical planning strategy，HPS)来实现拟人臂的仿人运动。HPS由2个判定条件(距离判定条件及姿态判定条件)和3个规划层组成。判定条件将完整的运动过程划分为不同的运动阶段，每一阶段又对应了不同的规划层。在不同的规划层下，拟人臂的运动方式有所不同。

2.1 触发条件

从运动过程的角度来看，触发条件的作用是对运动过程进行离散化。因此，触发条件的确定对于运动过程的解耦有着十分重要的作用。将NAO的参数代入到判定条件中，使其可以直接地应用到拟人臂仿人运动规划中。NAO手臂的关节配置按照生理关节划分可以定义为

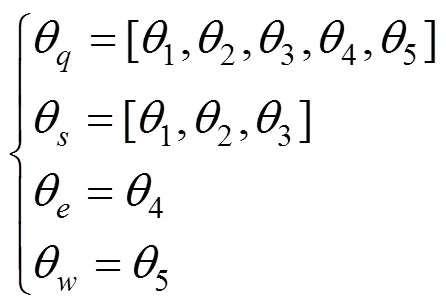
其中，θ为NAO手臂的机械关节；θ、θ和θ分别为NAO手臂的肩关节集合、肘关节集合和腕关节集合。

2.1.1 距离判定条件

在人臂运动过程中存在着一些关键臂姿，常发生在运动的开始阶段或结束阶段，并影响着整个运动过程。确定距离判定条件的目的是为了能够准确地划分出这些阶段。速度是影响人臂运动的重要因素，在生物力学等领域内关于人臂速度及关节角速度都进行了大量的研究[16-17]，因此本文利用相关研究成果来确定距离判定条件。在运动过程中，始末腕部关节差可以表示为

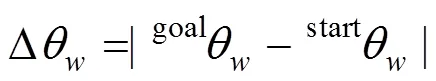
其中，start和goal分别为初始及目标腕部关节角。

腕关节的运动时间可以通过范数近似表达为

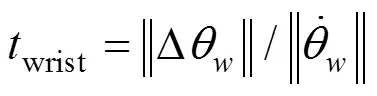
在HPS中，腕部的轨迹可以近似于一条直线[18]，因此手臂的运动时间可以表示为

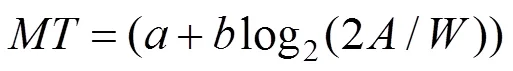
其中，为运动时间；和为回归系数；为初始点到目标点中心的距离；为目标区域的宽度。

手臂平均运动速度为

因此，判定距离条件可以表示为

2.1.2 姿态判定条件

通过基于采样的实验方法来获取姿态判定条件，如图3所示，共有10名志愿者参与到实验当中 (其中8名男性，2名女性，平均身高1.73 m，平均体重62.58 kg)。姿态判定条件主要是用来判断运动过程中特殊运动的发生与否，在运动过程中，当手部姿态与目标姿态接近时，手部姿态在接下来的运动中将保持不变，并会影响整个手臂的状态。因此需要确定姿态变化的临界值。在实验中，手部姿态proc可以通过计算实时获取，并以此计算目标姿态goal与手部姿态proc的差。实验内容为不同方向的抓取实验，图3所示为水平方向上的实验示意图，其中图3(a)所示为初始位姿，目标物体在实验者的胸前，图3(b)为目标位姿。实验中目标物体的距离及实验者手臂尺寸数据均进行归一化处理，并选取一组数据为基准数据，即

其中，S为基准量；r为目标物体到胸前的距离；l为手臂长度。对于其他实验者而言，目标物体距离胸前的距离可以表示为

其中，为其他实验者手臂长度。

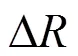
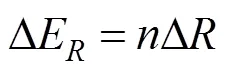
其中，为权系数。

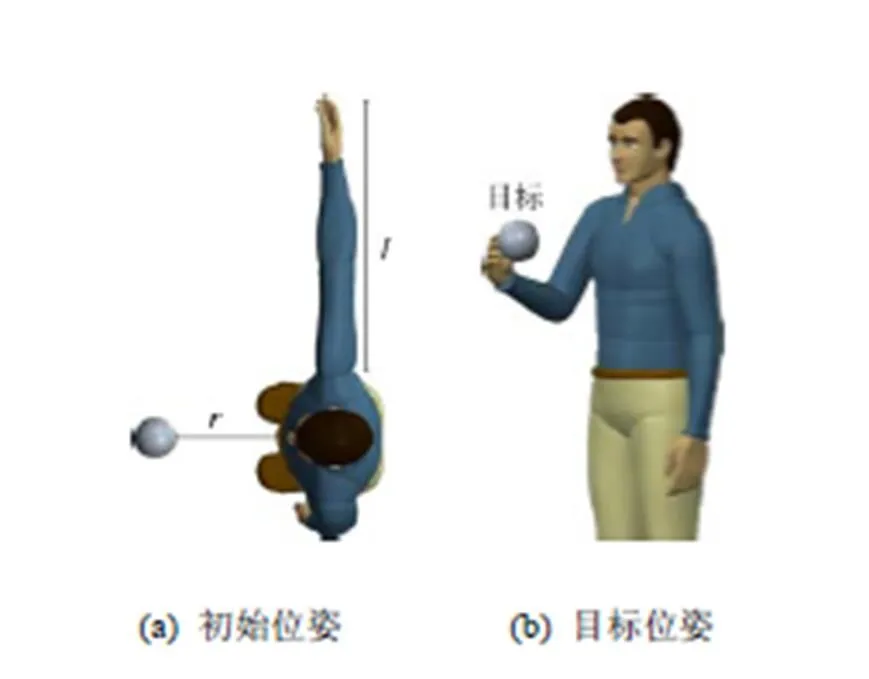
图3 姿态判定条件实验

2.2 规划层

触发条件将运动分为不同的阶段，每个阶段都有其特有的运动方式。

(1) 一级规划。从运动过程角度来看，人臂运动可以看作是移动和抓取的过程。一级规划所描述的就是移动的过程。在一级规划层中，并不需要考虑末端的姿态，腕部的运动以随动的形式呈现。

(2) 二级规划。二级规划描述的是抓取的过程，在运动过程中腕部运动起到了主导作用，决定了任务完成的质量。

(3)三级规划。三级规划描述的是运动中的一类特殊运动，即在运动过程中当手部姿态与目标姿态接近时，人臂将保持手部姿态不变的情况下完成整个运动。

2.3 分级规划算法

在HPS中，拟人臂的关节状态可以表示为

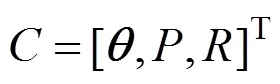
其中，(1,2,3,4,5)、(,,)和(,,)分别为NAO关节角、末端位置和姿态。根据目标臂姿假说[19]，人们的手臂在运动之前会根据目标信息在头脑中会预先确定最终的手臂姿态，即目标臂姿。因此根据目标臂姿假说，可以得到任务完成时最终的手臂臂姿。因此，初始状态Cstart和最终状态Cgoal可以根据任务条件及要求获得，过程量Cproc在运动过程中通过计算获得，则分级规划策略流程如图4所示。

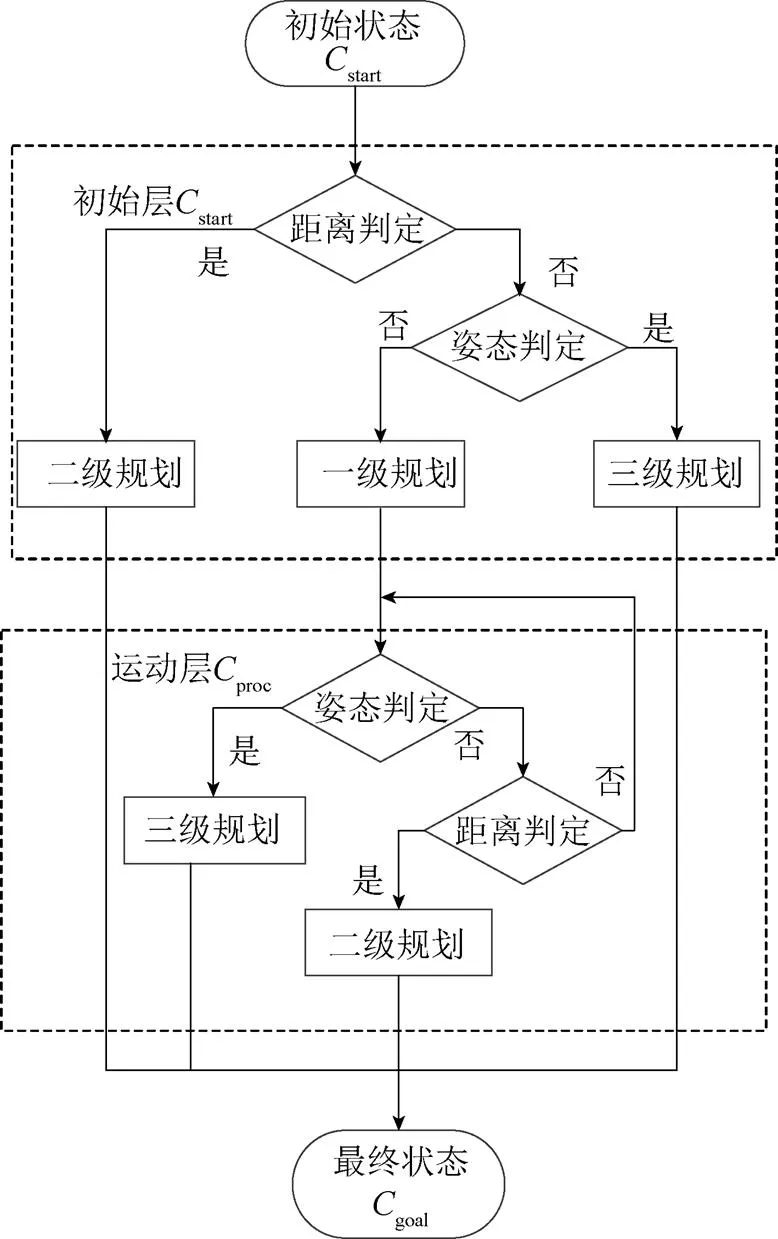
图4 分级规划策略流程图

具体HPS算法如下：

(1) 初始状态start和最终状态goal已知。过程量proc通过计算实时获取。

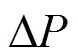
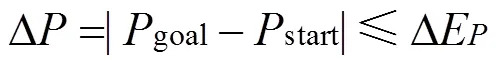
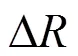
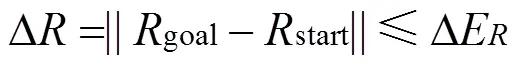
拟人臂在接下来的运动中采用三级规划。

(3) 当式(15)不满足时，即不满足姿态判定条件，拟人臂将采用一级规划。运动进入到运动层，过程量Cproc在运动过程中通过计算获取。

(4) 在运动层，选择规划层的方法与初始层中相同，过程量proc取代初始状态start来进行判定条件的计算。当规划层发生变化时，相应的拟人臂运动状态也发生改变。需要注意的是，过程量proc在运动过程中根据运动实时变化。

(5) 最终，通过二级规划或三级规划，拟人臂达到目标，即满足条件

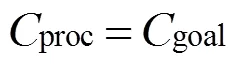
初始层与运动层的规划方法几乎一样，唯一不同的就是初始判定条件：在初始层，首先进行距离判定，而在运动层则是姿态判定。初始层适用于在运动开始前，目标物体非常接近末端执行器的情况，因此距离判定为第一优先级。在运动层，姿态判定为第一优先级。

3 臂姿预测指标

根据不同规划层的运动特点，分别建立了不同的臂姿预测指标。

3.1 一级规划层中臂姿预测指标

一级规划层中，由于不需要考虑末端姿态，因此拟人臂可以简化为达点运动模型，即仅考虑肩关节及肘关节。在日常生活中，达点运动是最常见的运动，本文利用最小势能指标[6](minimum total potential energy，MTPE)作为该规划层的臂姿预测指标。MTPE由重力势能(gravitational potential energy，GPE)和弹性势能(elastic potential energy，EPE)两部分组成，其表达式可定义为

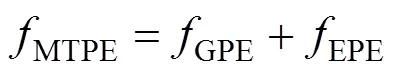
GPE可以通过下式计算得到，即

其中，m，m分别为大臂、小臂的质量；h、h分别为大臂、小臂质心的高度。

通过一种变系数的虚拟扭簧模型来计算MTPE，即

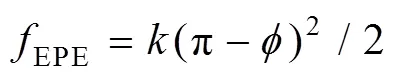
其中，为肘部旋转角；为弹簧系数，详细说明详见文献[6]。

因此，一级规划中的臂姿预测指标H为

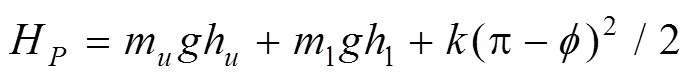
3.2 二级规划层中臂姿预测指标

在生物物理学中，达点运动是由大臂主导，而在抓取运动中，则是小臂起到主导作用。在运动中，小臂进行了大量的运动，而大臂受到小臂牵引靠着惯性进行随动，其运动距离相对较短，意味着肘关节运动距离较短。因此在二级规划层中，以肘关节最短距离为优化目标，设肘关节中心点的初始位置为(0,0,0),目标位置为(x,y,z),肘部距离最短可表示为

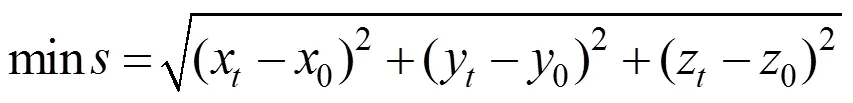
因此，二级规划层中的臂姿预测指标HS为

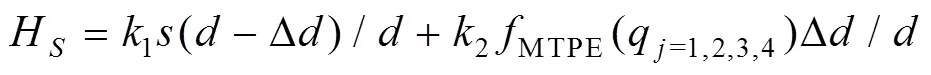
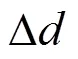
3.3 三级规划层中臂姿预测指标

三级规划描述的是手部姿态不变的特殊运动，因此取末端姿态最小变化为优化目标，其表达式为

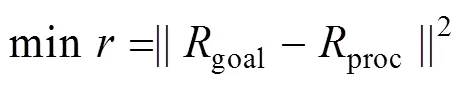
因此，三级规划中的目标函数H为

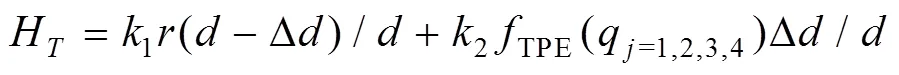
综上，HPS中的优化目标可表示为

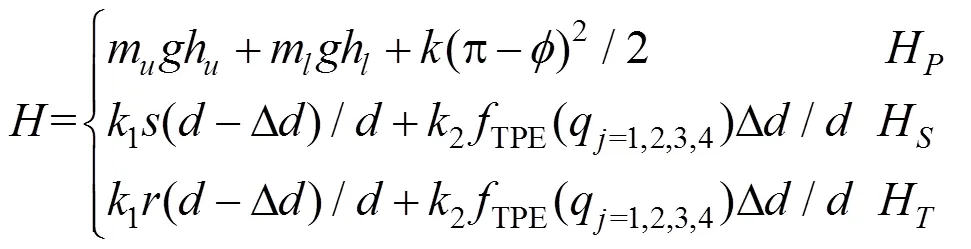
其中，权系数1、2及过渡项用来保证拟人臂在不同规划层中的平稳过度，防止关节角的突变。但当运动中只包含二级规划或三级规划，即运动中并未出现规划层的变化时，1及过渡项为1，2为0。

4 实验验证

4.1 实验设置

一共有20名志愿者参与到实验中，每名实验者需要完成12个达点运动实验，每个实验完成5次(20×12×5)。取每名实验者在不同点处的平均值与HPS在NAO平台上预测的值进行比较。这12个点在同一竖直面上按照3行4列的形式均匀分布，每两点之间间隔为10 cm。实验者们按要求以手臂自然下垂作为初始位姿开始运动，运动数据通过运动捕捉系统获取并作为比较数据(图5)。

图5 分级规划策略验证实验

利用梯度投影法(gradient projection method，GPM)来进行逆运动学的计算。GPM是一种基于广义逆的算法，其将逆运动学问题的解分为最小范数解和齐次解两部分，即GPM的表达式为

4.2 运动过程识别率

HPS主要用来实现运动过程的划分，因此首先验证运动过程中不同运动阶段的识别率。通过计算比较运动过程中规划层发生改变时末端位置与目标位置的距离来判定HPS运动预测的准确率。如图6所示，横坐标表示12个目标点，纵坐标表示运动过程解耦时末端位置与目标位置的距离。图中每一个柱形条代表实验者们在该点处的平均值(=[0.823 0.690 0.626 0.648 0.701 0.584 0.546 0.533 0.621 0.489 0.436 0.455])和标准偏差(=[0.054 0.062 0.068 0.072 0.051 0.074 0.081 0.081 0.073 0.080 0.089 0.083])。从图中可以看出，HPS中的触发条件不仅能够准确地判断出运动的变化，而且在针对不同个体时也依然具有一般性。

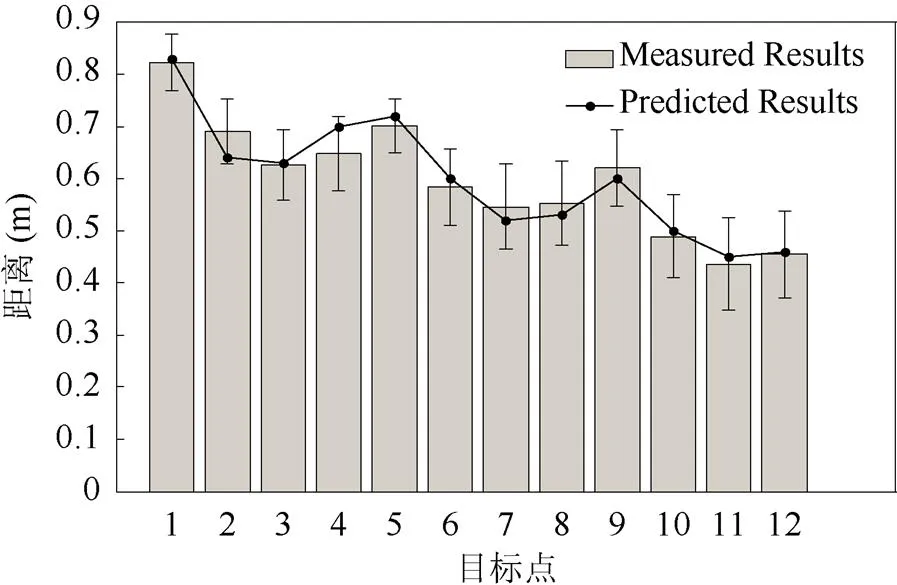
图6 运动过程识别率

4.3 静态臂姿预测

由于肩关节固定，末端位置已知，因此通过肘部预测值与实际值的误差来评价预测方法的性能。由于人臂与拟人臂尺寸不同，需要对图5中的目标点位置进行坐标变换，将其转换到拟人臂坐标下，从而在拟人臂坐标中进行臂姿预测比较[15]。为了验证HPS算法在不同规划层中的有效性，在不同规划层中随机选取目标点，利用HPS算法进行臂姿预测并与实际臂姿进行比较。比较结果如图7所示，红色虚线为拟人臂预测位姿，蓝色实线为手臂实际位姿，并在Blender软件中进行重现，以便观察。HPS在不同规划层中预测的拟人机械臂的臂姿都与人臂十分接近。

为了进一步验证本文提出HPS算法的性能，在仿人机器人平台NAO上分别利用精度较高的MTPE算法与HPS算法对图5中的12个目标点进行臂姿预测，并与实际臂姿进行比较。表2为两种算法在不同规划层下肘关节位置误差的平均值与方差对比。图8给出了其中3个实验点两种算法预测的臂姿对比。分析表2可以发现，HPS比MTPE具有更小的误差平均值，由于运动过程是复杂多样的，MTPE仅仅依靠单目标来预测臂姿存在着一定的局限性，并不能准确地反映运动过程中的所有情况，而本文提出的HPS算法将运动过程细分，根据不同运动过程的手臂运动特点，建立相应的臂姿预测指标，能够准确地预测出不同运动过程中的臂姿，因此具有较小的误差。同时，图8中也可看出HPS算法预测的臂姿与实际的臂姿非常接近，进一步表明其优越性。

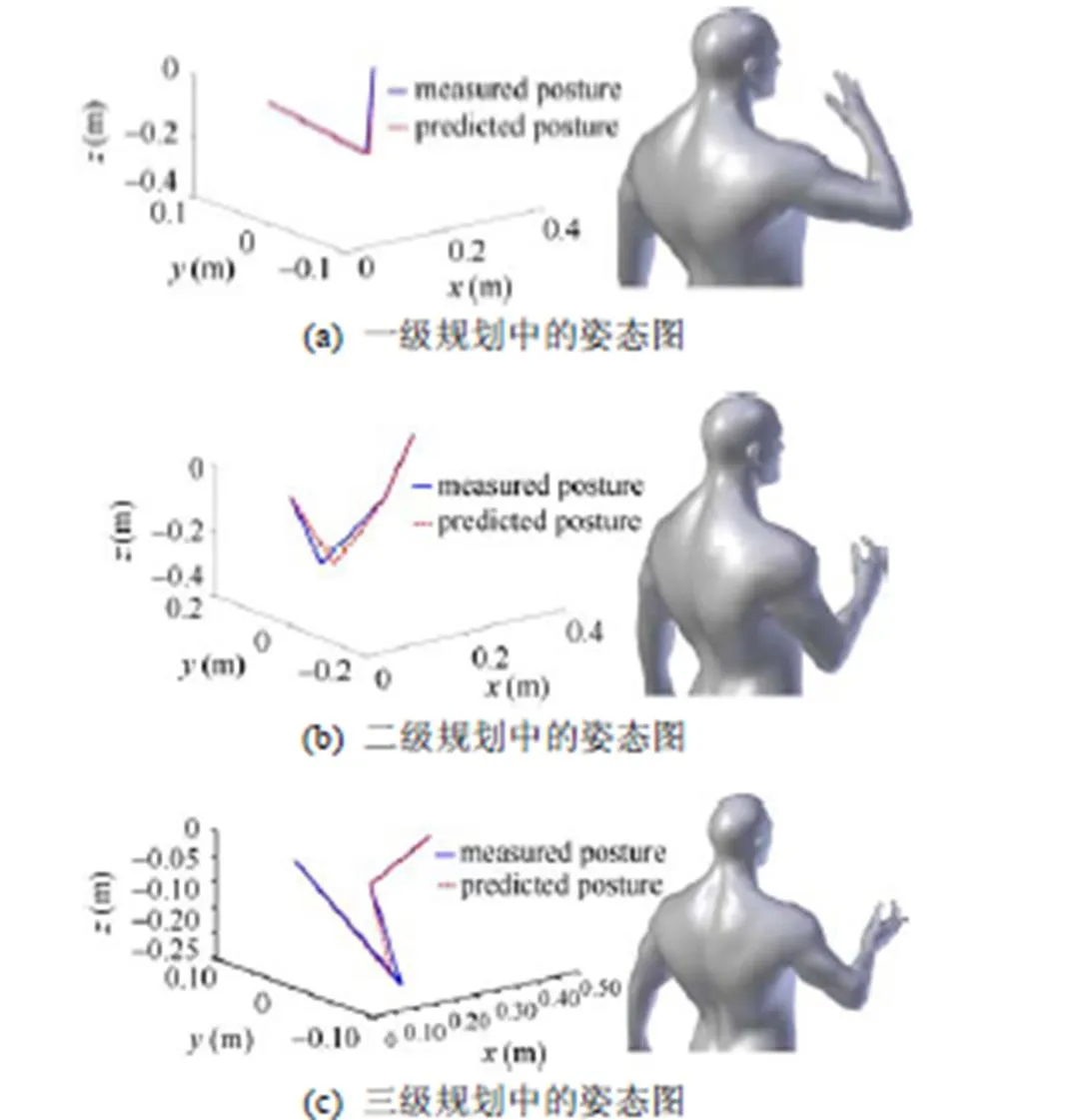
图7 实验者H的臂姿预测数据

表2 HPS算法与MTPE算法产生的肘关节位置在不同规划层中的比较(cm)

图8 静态臂姿预测对比

4.4 动态臂姿预测

通过比较整个运动过程中肘关节的位置与实际测量的位置的误差，来验证动态臂姿的相似性。利用HPS算法与MTPE算法在实验平台NAO机器人上达到图5中12个目标点的整个运动过程的预测臂姿比较。表3给出了两种算法预测整个运动过程肘关节位置的误差平均值与方差对比。

分析表3可以发现，对于动臂臂姿预测HPS比MTPE具有更小的误差平均值。图9为第二组实验中，利用HPS算法在NAO平台上规划得到的手臂臂姿与人臂实际臂姿的运动对比图；图10为该运动中NAO手臂的构型简图及利用HPS算法所规划的关节角。利用HPS算法，拟人臂能够在整个运动过程高度逼近真实人臂运动，从而准确地实现仿人运动。

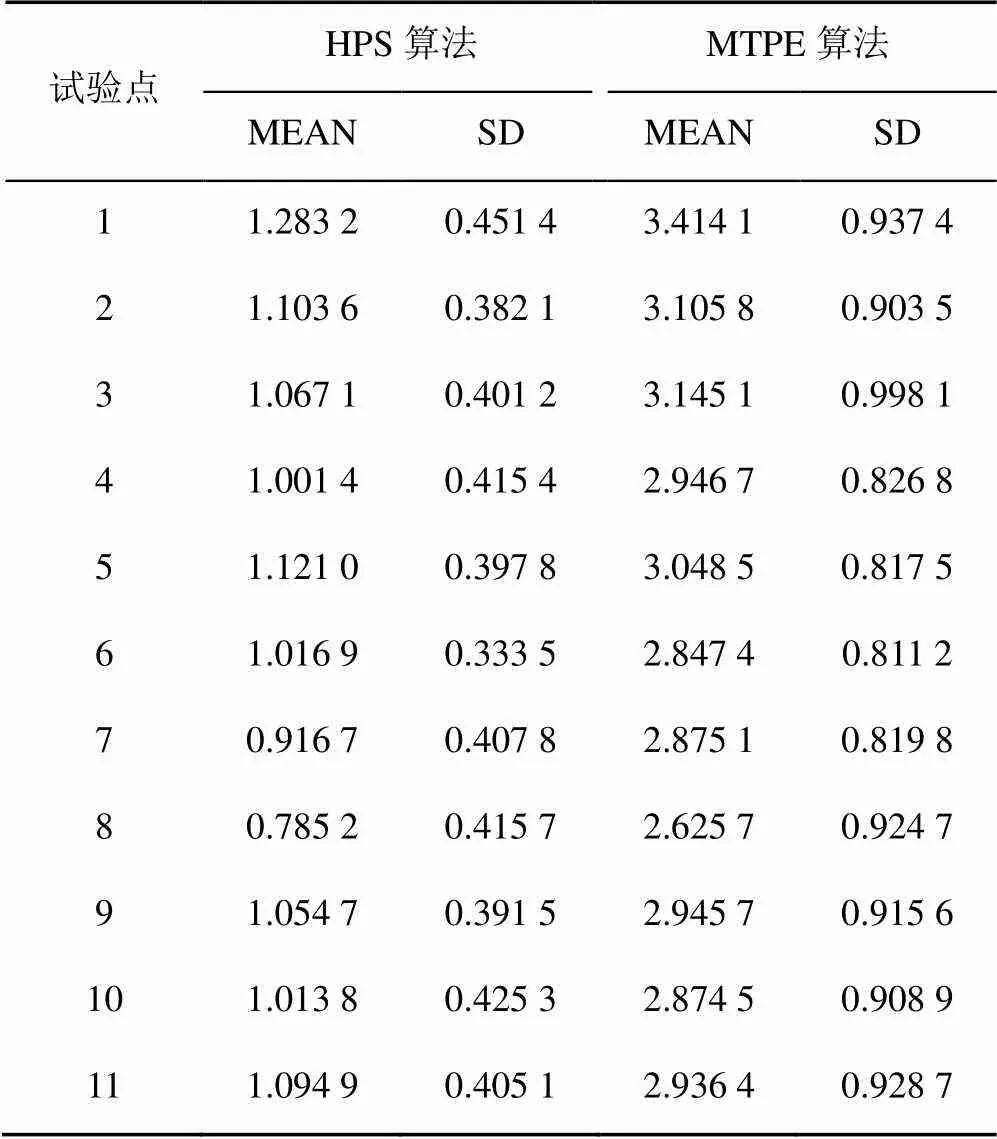
表3 动态臂姿预测值(cm)

图9 实验者与NAO手臂运动对比图

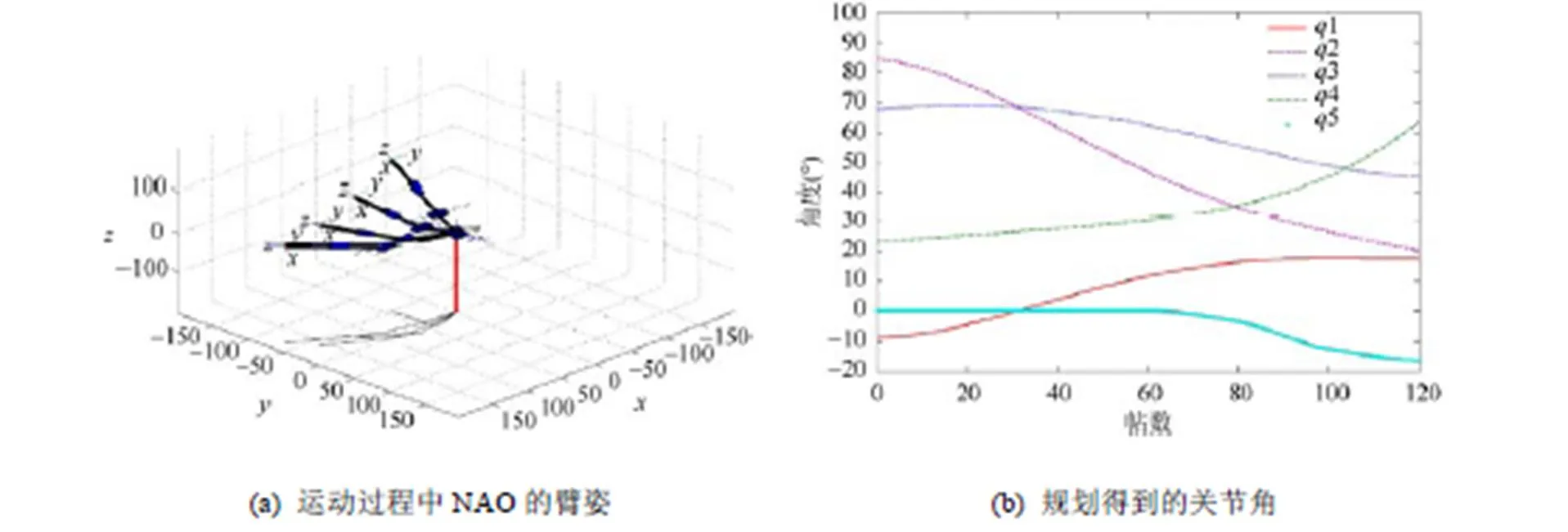
图10 利用HPS规划所得的达点运动

综上所述，本文提出的HPS算法将运动过程细分，根据不同运动过程的手臂运动特点，建立相应的臂姿预测指标，能够准确预测出不同运动过程中静态臂姿，与复杂的动态臂姿。从对比结果中可以看出，无论是静态预测还是动态预测，通过HPS算法所得到的肘部误差平均值均低于MTPE算法。因此，利用本文提出的HPS算法能够使拟人机械臂具有高度逼真的仿人运动。

5 结束语

本文提出了一种拟人臂分级规划策略，对人臂运动过程进行划分，确定影响运动过程变化的约束条件，并进行了定量化的表达。通过建立不同运动过程中的规划层，在不同的规划层中，拟人臂具有不同的运动特点，根据拟人臂的特点，建立了各个规划层下的运动臂姿预测指标，并利用梯度投影法实现了拟人臂仿人运动规划。最后，在仿人机器人NAO为实验平台上，验证所提出的HPS算法与MTPE算法的静态、动态臂姿预测，并与真实人臂运动数据进行比较。实验表明，所提出的HPS算法具有较小的预测误差，能使拟人机械臂产生高度逼真的仿人运动。同时，该方法也同样适用于运动过程简单、重复性高同时对末端路径具有较高要求的新型工业机器人，使其在与人共同完成任务时具有更高的效率。

[1] LAW J, SHAW P, LEE M, et al. From saccades to grasping: a model of coordinated reaching through simulated development on a humanoid robot [J]. IEEE Transactions on Autonomous Mental Development, 2014, 6(2): 93-109.

[2] 曾德标, 万世明, 李迎光, 等. 装配机器人加工站位设置混合优化算法[J]. 图学学报, 2016, 37(4): 496-501.

[3] 许国玉, 曹虎辰, 刘少刚. 基于特征线段匹配的救援机器人建图方法[J]. 图学学报, 2013, 34(4): 83-87.

[4] YANG J, MARLER T, RAHMATALLA S. Multi-objective optimization-based method for kinematic posture predication: development and validation [J]. Robotica, 2011, 29(2): 245-253.

[5] KIM H, LI Z, MILUTINOVIC D, et al. Resolving the redundancy of a seven DOF wearable robotic system based on kinematic and dynamic constraint [C]// IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2012: 305-310.

[6] ZHAO J, XIE B Y, SONG C Y. Generating human-like movements for robotic arms [J]. Mechanism and Machine Theory, 2014, 81(11): 107-128.

[7] WANG X, VERRIEST J P. A geometric algorithm to predict the arm reach posture for computer-aided ergonomic evaluation [J]. Journal of Visualization and Computer Animation, 1998, 9(1): 33-47.

[8] LIU W H, CHEN D S, STEIL J. Analytical inverse kinematics solver for anthropomorphic 7-DOF redundant manipulators with human-like configuration constraints [J]. Journal of Intelligent & Robotic Systems, 2017, 86(1): 63-79.

[9] CORDELLA F, ZOLLO L, SALERNO A, et al. Human hand motion analysis and synthesis of optimal power grasps for a robotic hand [J]. International Journal of Advanced Robotic Systems, 2014, 11(1): 1-13.

[10] ROSELL J, SUAREZ R, ROSALES C, et al. Autonomous motion planning of a hand-arm robotic system based on captured human-like hand postures [J]. Autonomous Robots, 2011, 31(1): 87-102.

[11] 袁丽, 田国会, 李国栋. NAO机器人的视觉伺服物品抓取操作[J]. 山东大学学报: 工学版, 2014, 44(3): 57-63.

[12] ZHANG L, WANG L, GUO L, et al. A method for humanoid robot pushing task based on teleoperation with human motion recognition [J]. Diangong Jishu Xuebao/Transactions of China Electrotechnical Society, 2015, 30(s1): 536-542.

[13] 卫沅, 赵京. 基于运动捕捉下的7R机械臂的实时控制[J]. 机械工程学报, 2013, 49(23): 68-73.

[14] ALIBEIGI M, RABIEE S, AHMADABADI M N. Inverse kinematics based human mimicking system using skeletal tracking technology [J]. Journal of Intelligent Robot System, 2017, 85(1): 27-45.

[15] ARTEMIADIS P K, KATSIARIS P T, KYRIAKOPOULOS K J. A biomimetic approach to inverse kinematics for a redundant robot arm [J]. Autonomous Robots, 2010, 29(3-4): 293-308.

[16] TAKEDA Y, IWAHARA M, KATO T, et al. Analysis of human wrist joint impedance: does human joint viscosity depend on its angular velocity [C]//IEEE Conference on Cybernetics and Intelligent Systems. New York: IEEE Press, 2004: 999-1004.

[17] LIVESON J, SHETTY J. Ulnar nerve conduction velocity as function of wrist position [J]. American Journal of Physical Medicine & Rehabilitation, 2001, 80(5): 380-382.

[18] FLASH T, HOGAN N. The coordination of arm movements: an experimentally confirmed mathematical- model [J]. Journal of Neuroscience, 1985, 5(7): 1688-1703.

[19] XIE B Y, ZHAO J, LIU Y. Human-like motion planning for robotic arm system [C]//IEEE 15th International Conference on Advanced Robotics. New York: IEEE Press, 2011: 88-93.

On Human-Like Motion Planning Algorithm of Anthropomorphic Mechanical Arms Based on Hierarchical Planning Strategy

WANG Chunrong1, XIA Erdong1, ZHAO Jing2, XIONG Changjiong1, LIU Jianjun1, WEI Yuan3

(1. School of Mechanical & Electronic Engineering, Sanming University, Sanming Fujian 365004, China; 2. School of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China; 3. School of Vehicle and Traffic Engineering, Henan University of Science and Technology, Luoyang Henan 471003, China)

In order to make anthropomorphic mechanical arms generate human-like movements accurately, a novel human-like motion planning method is proposed, which combines the trigger conditions and hierarchical planning strategy (HPS). The method decomposes the complete arm movements into a set of different motion processes, each of which has corresponding planning hierarchies. The anthropomorphic mechanical arms reveal different characteristics in different planning hierarchies. The motion models and posture prediction indicators in varying planning hierarchies are built based on the respective characteristics to predict the postures of anthropomorphic mechanical arms. The experiment is acted on humanoid robot NAO as the platform, and then the prediction results of static and dynamic arm postures is performed by the proposed method and the minimum total potential energy (MTPE) are compared. In addition, the prediction results are compared with the real arm motion data collected by motion capture system (OptiTrack). The experimental results show that the errors of static and dynamic posture prediction of proposed method could be reduced, and the anthropomorphic mechanical arms can generate the human-like movements accurately through the proposed method.

anthropomorphic mechanical arms; human-like movements; hierarchical planning strategy; arm posture prediction

TP 241

10.11996/JG.j.2095-302X.2018030553

A

2095-302X(2018)03-0553-09

2017-10-24；

2017-12-21

国家自然科学基金项目(51475016)；福建省自然科学基金项目(2016J01741)；福建省教育厅科技项目(JAT170531)；福建省引导性项目(2016N0029)；三明市科技项目(2014-G-6)

王春荣(1986-)，男，福建漳州人，讲师，博士。主要研究方向为机器人运动学与动力学。E-mail：callchunrong@foxmail.com

夏尔冬(1986-)，女，湖北黄冈人，讲师，硕士。主要研究方向为人工智能。E-mail：382831159@qq.com