对称不变形状上下文特征提取与匹配
贾耕云,赵海英,周 倩,李学明
对称不变形状上下文特征提取与匹配
贾耕云,赵海英,周 倩,李学明
(北京邮电大学信息与通信工程学院,北京 100876)
形状上下文是一种广泛应用的图像形状特征提取与匹配算法,针对其特征不具有对称不变性,无法对互相对称的相似图像建立匹配的问题,提出了一种具有对称不变性的改进形状上下文特征提取与匹配算法。在形状边缘采样点上计算形状上下文中的角度关系描述时,令该点的梯度方向为极坐标系的0°,并比较特征0到π与π到2π两个角度区间内其他边缘点的数量大小,根据比较结果,调整极坐标系中角度增加的方向,从而使特征具备对称不变性。在迭代变形与计算形状上下文时,仅在第一次迭代中使用改进的形状上下文特征,从而使匹配更加稳定。仿真实验证明,该算法能够有效地在互相对称的相似图像间建立匹配,提高检索精度。
图像匹配;形状上下文;对称不变性;匹配稳定性
形状特征是一类重要的图像特征,其中形状上下文(shape context)[1-2]是一种应用广泛的图像形状特征,该方法使用图像轮廓点作为特征点,在对数极坐标系下计算每一点与轮廓上其他点的位置关系组成直方图,在很多匹配、识别、检索任务上都取得了较好的效果,如MNIST[3]字体识别等。该算法在处理非线性形变以及少量离群点时具有一定的鲁棒性,并具有平移、尺度和旋转不变性。
在现实生活中,互相对称的相似图像广泛存在。如图1所示,两幅图像中的形状以竖直方向为对称轴互相对称,且由于形状不具备自身对称性,即不存在任何直线,使以该直线为对称轴进行对称变换后的图像与原图一样,所以一个形状无法通过旋转得到另一个。

图1 互相对称的形状与形状上的对应点
形状上下文特征不具备对称不变性,当在互相对称的两个形状的对应点上,如图1中红框里的两个顶点上,分别提取形状上下文特征时,差别会很大,从而无法对两个形状建立正确的匹配,也无法对含有这种图像的集合进行有效地检索。一种直接的解决方法是对数据集中的每个图像,都增加对称变换的图像,然后对两个图像进行匹配,但这种方法将大幅增加运行时间,效率较低。为解决该问题,本文提出了一种改进的形状上下文特征提取方法,其以边缘点梯度方向作为特征极坐标起始方向,并根据该边缘点两侧其他点的数量,对极坐标旋转方向进行调整,从而使形状特征具备对称不变性。与传统形状上下文算法相比,该方法能有效地直接在对称图像之间建立匹配关系。
1 研究现状
图像检索与匹配基于如颜色、纹理、形状、空间位置等图像的各种特征,根据情况单独或联合使用。此外还有一些难以直接描述其物理含义的特征,如SIFT(scale-invariant feature transform)特征[4]等,对图1中所示的二值形状图像,其没有丰富的局部灰度变化与分布特征,因此SIFT等基于灰度梯度统计的方法难以有效提取特征,而其含有清晰的形状边界信息,对这种图像,使用形状特征进行匹配和检索效果最好。
基于形状特征的匹配与检索,其核心在于形状特征的提取,迄今为止已有很多方法被提出,可分为函数表示法、多边形近似、内部空间关系特征、尺度空间法以及变换域方法等[5]。形状上下文描述的是一种形状的内部空间关系特征,在这一类形状特征提取方法中,比较典型的还有链 码[6]、基于中轴的shock graph[7]以及基于张量尺度的方法[8]等。
针对形状上下文方法,MORI等[9]提出了剪枝形状上下文方法,只计算部分轮廓点的形状上下文特征来表示轮廓,或对形状上下文进行向量量化,提高了图像检索效率。XIE等[10]则提出基于形状骨架以优化边缘采样,并根据骨架端点建立一个由粗到细的匹配框架,降低计算复杂度,减少了计算时间。温丽华和赖康生[11]将形状上下文与序贯相似性检测结合起来,缩短了非匹配字符的匹配时间,提高了效率。徐衍鲁等[12]提出将SIFT与形状上下文结合,将两种特征级联匹配。郑丹晨和韩敏[13]提出一种利用角点典型形状上下文特征进行快速形状识别的方法,仅以少数角点作为代表点生成直方图,对目标形状关键特征进行描述,通过减少匹配的特征数目降低了采样点匹配时间。吴晓雨等[14]提出寻找采样点最多的角度区间的方法改变图像角度,从而给出了加入旋转不变性的另一种方法。
上述方法均对形状上下文特征提取与匹配算法进行了一定程度的改进,但均未解决传统算法不具备对称不变性的问题。
2 基于形状上下文的图像特征提取与匹配
(1) 特征提取。首先提取目标形状的边缘并随机采样边缘点(图2(a)~(b)),并计算边缘点的方向,然后再采用如图2(c)所示的极坐标系统对每个点计算其他与剩余边缘点的位置关系,其中距离根据图中点之间的平均距离归一化,得到如图2(d)所示的形状上下文直方图。
(2) 匹配。首先对两组边缘点根据其形状上下文和边缘方向特征计算相似度,用Hungarian算法得到两组边缘点的匹配,如图3所示;然后对待匹配图像进行仿射和薄板样条(thin plate spline,TPS)变换,使待匹配图变形为与目标图更相似的图像,并计算变形后的特征相似度。重复以上计算相似度-匹配-变形的步骤直至预设的变形次数。

图2 形状上下文特征提取

图3 形状匹配对应点
关于旋转不变性,文献[2]介绍了一种为形状上下文特征引入旋转不变性的方法,在计算直方图时定义边缘点的切向量方向为极坐标0°,使特征具备旋转不变性。
3 对称不变性形状上下文特征提取与匹配
3.1 对称不变性
图像的对称变换改变图像点与点之间的角度位置关系,但距离关系不变。如对图像沿竖直轴做左右对称变换,则对应点的左右位置关系反转。为使形状上下文特征能够在对称变换中保持不变,应使特征极坐标中的角度部分做相应变换。即需对极坐标系0°位置和角度增加的方向(顺时针或逆时针)做相应调整,如图4所示。

图4 极坐标0°位置与角度增加方向示意图
定位极坐标系0°位置。以该点的梯度方向作为极坐标系中的0°,由于点梯度方向会随对称变换进行相应变换,因此该方法可以使0°位置具备对称不变性。
对角度增加的方向。考察面向梯度方向时需考虑该点左右两侧其他边缘点的数量,角度从数量多的一侧开始增加。若两点是两个互相对称图像中的对应点,则其应以梯度方向开始,互相反向旋转一周才能获得相同的形状上下文特征描述。同时,梯度方向的左右两侧点的数量多数情况下也具有这种反向性,因此该方法可使角度增加的方向具备对称不变性。在图4(a)中梯度方向右侧半圆区域内边缘点多,角度顺时针增加;图4(b)梯度方向左侧半圆区域内边缘点多,角度逆时针增加。
3.2 匹配稳定性
通过定义梯度方向为极坐标0°,然后自适应改变角度增加方向,引入对称不变性并保持了旋转不变性,但该方法提取的特征稳定性有所降低,更容易使非对应部位出现相似的特征,这种问题在引入文献[2]的旋转不变性时也会出现。
为了解决这个问题,在迭代计算形状上下文与图像变形的流程中,仅在第一次迭代时使用对称不变的形状上下文提取算法,经过一次TPS变换后,使用传统的形状上下文特征(无旋转不变性)。由于对称不变形状上下文特征在第一次匹配时能够提供足量的正确匹配,因此第一次TPS变换能够判断目标图像是否与待匹配图对称,进而使目标图像实现对称变形,如图5所示,这使得第二次迭代时目标图与待匹配图恢复非对称关系,从而能够使用稳定性更高的传统形状上下文匹配算法。
若两幅图像仅有一部分相互对称,使用提出的改进算法,可以在第一次迭代匹配时得到基本正确的匹配结果。但由于在后续的迭代匹配与变形中对图像进行的是全局变形,从而在第二次及以后的匹配中,匹配效果会变差,因此本算法只能对局部对称的图像进行一次粗略匹配,无法通过多次变形获得高精度的匹配。

图5 互相对称的相似图像以及第一次TPS变换结果
((c)中蓝色“+”为(a)经过一次TPS变换的结果)
3.3 算法与分析
本文算法具体步骤为:

步骤2. 根据当前循环次数的取值,选择计算形状上下文直方图的方法,其中距离关系计算在两种方法中一致,区间划分均采用对数形式,并使用所有点距离的均值进行归一化。



若>1,则按照传统形状上下文匹配算法计算特征,最终角度值即为初始角度,即



其中,为形状上下文的直方图,而边缘点角度差为


根据损失矩阵,对两组采样点用Hungarian算法进行匹配,得到匹配损失最小的一组对应关系,即
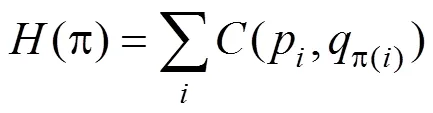
步骤4. 根据采样点的对应关系,对目标形状图像进行TPS变换,使目标形状按照与原形状图像更相似的方向变形,得到目标形状的一组新的采样点。


算法分析:
在每一次循环中,均根据上一次的匹配结果对一幅图像进行TPS变换,变换使得两幅图像上互相对应的边缘点之间距离降低。因此图像更加相似,从而两幅图像形状上下文特征的卡方距离得以降低,具体变换的过程参考文献[2]。虽然本文算法引入了对称不变性,但仅在第一次循环中使用了改进的形状上下文特征,因此收敛性得以保持。
为了降低离群点的影响,本文算法还在式(6)的损失矩阵中引入虚拟点,一旦某个点与其他所有点的损失都高于给定阈值,则该点会与虚拟点进行匹配,因此互相匹配的点都能够保持一定程度的相似性,增强了算法的鲁棒性。

4 仿真实验与分析
4.1 数据集与参数设置
为验证改进形状上下文特征匹配算法的有效性与准确性,在MPEG-7数据集中,选择了100个形状作为图像集,该图像集中有互相对称的相似图像,但每个图像都不具备自身对称性,100个图像共分为10类,每类10个。另外还收集了一些典型民族服饰图案作为图像集,包含10类共59个形状图案。如图6所示,在这两个数据集上分别进行匹配与检索仿真实验。

4.2 仿真实验
4.2.1 对称图像匹配实验


图6 实验用数据集

图7 形状上下文损失变化曲线
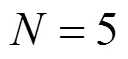

图8 匹配实验部分结果
如图8所示,本文算法能够对互相对称的图像建立较为准确的匹配,包括部分形变(图8(a)中第1列的鸟图案和第3列的锤子图案)以及旋转(图8(a)中的锤子图案)的情况下仍有良好的匹配效果,而传统算法则无法使对应点建立匹配。
4.2.2 检索实验


图9 检索实验结果
由图9可以看出,本文提出的对称不变形状上下文算法在100个MPEG-7图像上检索效果略优于IDSC算法,且明显优于传统形状上下文算法(包括没有和有旋转不变性两类),在传统民族服饰图案检索上,本文算法效果明显优于其他算法。实验还验证了匹配稳定性问题,如图中红色“*”曲线所示,若在4次迭代中均使用对称不变形状上下文特征,其检索效果弱于旋转不变的传统形状上下文算法。
5 结束语
本文针对形状上下文特征提取与匹配算法不具备对称不变性的问题,提出了一种改进的形状上下文算法。算法在提取形状上下文特征时,令采样点的梯度方向为极坐标0°,并比较梯度方向两侧采样点数量,调整极坐标角度增加方向,使特征获得对称不变性;同时,在迭代匹配步骤中,仅在第一次迭代使用对称不变特征,加强了匹配的稳定性。实验证明,本文算法能有效地对互相对称的相似图像建立匹配,并提高检索的准确率。
[1] BELONGIE S, MALIK J, PUZICHA J. Shape context: a new descriptor for shape matching and object recognition [C]//NIPS’00 Proceedings of the 13thInternational Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2001: 831-837.
[2] BELONGIE S, MALIK J, PUZICHA J. Shape matching and object recognition using shape contexts [J]. IEEE Transactions on Pattern Analysis and MachineIintelligence, 2002, 24(4): 509-522.
[3] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition [J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[4] LOWE, D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[5] YANG M Q, KPALMA K, RONSIN J. A survey of shape feature extraction techniques [M]//Pattern Recognition Techniques, Technology and Applications. Vienna: IN-TECH Open Access Publisher, 2008: 43-90.
[6] IIVARINEN J, VISA A J E. Shape recognition of irregular objects [C]//Proceedings of SPIE 2904: Intelligent Robots and Computer Vision XV: Algorithms, Techniques, Active Vision, and Materials Handling. Berlingham: the International Society for Optics and Photonics, 1996: 25-32.
[7] SIDDIQI K, SHOKOUFANDEH A, DICKINSON S J, et al. Shock graphs and shape matching [J]. International Journal of Computer Vision, 1999, 35(1): 13-32.
[8] ANDALÓ F A, MIRANDA P A V, TORRES R S, et al. Shape feature extraction and description based on tensor scale [J]. Pattern Recognition, 2010, 43(1): 26-36.
[9] MORI G, BELONGIE S, MALIK J. Efficient shape matching using shape contexts [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(11): 1832-1837.
[10] XIE J, HENG P A, SHAH M. Shape matching and modeling using skeletal context [J]. Pattern Recognition, 2008, 41(5): 1756-1767.
[11] 温丽华, 赖康生. 基于形状上下文的字符识别算法的改进[J]. 工业控制计算机, 2014, 27(7): 137-139.
[12] 徐衍鲁, 马燕, 李顺宝, 等. 结合颜色不变量的SIFT和形状上下文图像匹配算法[J]. 计算机科学, 2014, 41(Z11): 144-146,177.
[13] 郑丹晨, 韩敏. 基于改进典型形状上下文特征的形状识别方法[J]. 计算机辅助设计与图形学学报, 2013, 25(2): 215-220.
[14] 吴晓雨, 何彦, 杨磊, 等. 基于改进形状上下文特征的二值图像检索[J]. 光学精密工程, 2015, 23(1): 302-309.
[15] ZHENG Y, DOERMANN D. Robust point matching for nonrigid shapes by preserving local neighborhood structures [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(4): 643-649.
Symmetry Invariance Shape Context Feature Extraction and Image Matching
JIA Gengyun, ZHAO Haiying, ZHOU Qian, LI Xueming
(School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China)
Shape context is a popular algorithm of image shape feature extraction and matching, traditional shape context algorithm lacks symmetry invariance, which means it can not match two similar but symmetrical shapes. To overcome this shortcoming, this article proposed an improved shape context algorithm with symmetry invariance. The method defines the gradient direction of a sample point as its 0 rad in log polar coordinates when computing the angle relations in shape context, then compare the number of sample points in 0 rad to π rad and π rad to 2π rad, and adjust the angel increasing direction in the coordinate according to the results. In the process of iterative shape warping and shape contexts calculation, the symmetry invariance descriptors are only applied in the first iteration to obtain a more stable matching result. Experimental results show that the proposed algorithm can effectively establish match between two similar and symmetrical shapes, and therefor improve the retrieval precision.
image matching; shape context; symmetry invariance; matching stability
TP 391
10.11996/JG.j.2095-302X.2018030470
A
2095-302X(2018)03-0470-07
2017-01-14;
2017-05-11
国家自然科学基金项目(61163044);北京市科委基金课题(D171100003717003);财政部项目(GSSKS-2015-035)
贾耕云(1992–),男,山东泰安人,硕士研究生。主要研究方向为文化计算与模式识别。E-mail:jiagengyun@bupt.edu.cn
赵海英(1972–),女,山东烟台人,副教授,博士。主要研究方向为文化计算与模式识别。E-mail:zhaohaiying@bupt.edu.cn

