曹冲称象与思维转换

王林 戚婷婷

小朋友，你听过曹冲称象的故事吗？在曹冲五六岁的时候，有一天，孙权送来了一头大象，曹操想知道这头大象的质量，可是没有人能想出办法，因为那时候没有能称大象的大秤。曹冲说他有办法。他让人把大象赶到船上，在船贴近水面的地方做上记号，然后把大象赶下船，往船上装石头，当水面达到记号的时候，再称船上这些石头的质量，这样就知道大象的质量了。曹冲在这里进行了“等量代换”，也就是进行了思维的转换。

其实，在解决数学问题时，也常常用到这种思维转换。不信？你来看。

例1.星期天，淘气去爬山。他沿着一条长为12千米的路上山，然后原路返回。上山每小时走2千米，下山每小时走6千米。你知道淘气在上下山过程中的平均速度吗？

[分析与解]看完题目，可能你会说，这有什么呀，谁不会呢，（ 2+6）÷2，直接计算就可以了。果真如此吗？不需要“思维转换”吗？如果你真的这样想，就错了。

要解决的问题是“淘气在上下山过程中的平均速度”，注意是“上下山全过程”，因此，应该是上山和下山的总路程除以上山和下山所用的总时间。上、下山总路程为“12×2”千米，上山时间为“12÷2”小时，下山时间为“12÷6”小时。所以上下山过程中的平均速度为12×2÷（12÷2+12÷6） =3（千米/时）。

例2.李老师买了3千克苹果和5千克梨，共付款19元；张老师买了5千克苹果和3千克梨，共付款21元。小朋友，你知道苹果和梨每千克多少元吗？

[分析与解]观察题目中的数据，你是不是觉得挺简单的？李老师买了苹果和梨共8千克，张老师买了苹果和梨也是共8千克，另外，两位老师共买苹果3+5=8（千克），共买梨也是5+3=8（千克），所以列算式（ 19+21）÷2即可求出苹果和梨的价钱了。怎么样，是不是觉得自己这样计算挺牛的呀？其实这样计算是错的。

不妨把你的思维转个弯，转换一下。先把已知条件列出来：

苹果：3千克 梨：5千克 共19元

苹果：5千克 梨：3千克 共21元

你会发现，两人所买的苹果、梨的质量不同，钱数也不相同。如果能让苹果的质量或梨的质量相同，这个问题是否更容易解决呢？当然了，它们之间基本的数量关系是不能改变的。

可以用“扩倍法”让苹果或梨的质量相同。所谓的扩倍法就是把苹果、梨和钱数扩大相同的倍数。

方法1：把苹果的质量转换成相同。

把李老师买的水果质量和钱数分别乘5，张老师买的水果质量和钱数分别乘3，这样两位老师买的苹果的质量数就相同了，而不同的仅仅是梨的质量数和钱数。

苹果：3×5千克 梨：5×5千克 共19×5元

苹果：5×3千克 梨：3×3千克 共21×3元

通过观察发现：两位老师付款的总钱数不同，这是因为两人买的梨的质量不同。每千克梨的价格为（ 19×5-21×3）÷（5×5-3×3）=2（元），每千克苹果的价格为（ 19-2×5）÷3=3（元）。

方法2：把梨的质量数转换成相同。

把李老师买的水果质量和钱数分别乘3，张老师买的水果质量和钱数分别乘5，这样两位老师买的梨的质量数就相同了。

苹果：3×3千克 梨：5×3千克 共19 ×3元

苹果：5×5千克 梨：3×5千克 共21 ×5元

通过观察发现：两位老师付款的总钱数不同，这是因为两人买的苹果的质量不同。每千克苹果的价格为（ 21×5-19×3）÷（5×5-3×3） =3（元），每千克梨的价格为（19-3×3）÷5=2（元）。

方法3：把两位老师买的水果数和钱数分别加在一起，可知8千克苹果和8千克梨共“19+21”元，所以1千克苹果和1千克梨共（19+21）÷8=5（元）。

3千克苹果 5千克梨 共1 9元

1千克苹果 1千克梨 共5元

小朋友，后面的计算你自己完成吧！怎么样，有信心吗？试试转换思维呦！

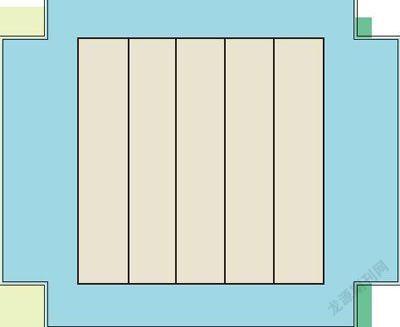
例3.一个正方形被分成了五个小长方形（如右图），每个小长方形的周长都是48厘米，你知道这个正方形的周长是多少吗？

[分析与解]读完题目，是不是有点儿郁闷？要求出正方形的周长，一般来说需要知道正方形的边长。可是，这里不仅不告诉这些条件，居然还把正方形分成了五个小长方形。好在告诉了每个小长方形的周长。不过，知道这些有什么用呢？

你不妨转换一下思维，很容易发现正方形与这五个小长方形之间的关系。小长方形的长与正方形的边长相等，五个小长方形的宽之和与正方形的边长相等，因此，小长方形的长是宽的5倍（想想为什么）。

小長方形周长的一半（即一条长和一条宽）是48÷2=24（厘米）。把小长方形的宽看作1份，则长是5份，小长方形的宽是24÷（1+5）=4（厘米），长（即正方形的边长）是4×5=20（厘米），所以正方形的周长是20×4=80（厘米）。

思路一变天地宽。怎么样，问题解决了吧！你想对了吗？

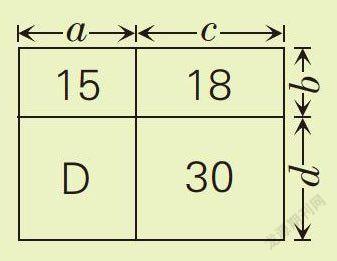
例4.把一块长方形菜地分成4个小长方形（如右图），已知长方形A的面积是15平方米，长方形B的面积是18平方米，长方形C的面积是30平方米，问长方形D的面积是多少平方米？

[分析与解]题中要求“长方形D的面积是多少平方米”，可是长方形的长和宽一个都不知道。不要着急，你不是学会了“转换思维”吗？先不要忙着计算，咱们来玩个“假设游戏”，假设长方形A的长为a米，宽为6米（自己试着在图形上标出对应的字母），则其面积为“a×b”平方米。同理，设长方形C的长为c米，宽为d米，则其面积为“c×d”平方米。同时可以发现，长方形B的面积为“b×c”平方米。长方形D的面积为“a×d”平方米。如果把A和C两个长方形的面积相乘，得到“A×C=a×b×c×d”平方米。同样把B和D两个长方形的面积相乘，得到“B×D=b×c×a×d”平方米。

至此发现：A和C两个长方形的面积相乘=B和D两个长方形的面积相乘。因此，长方形D的面积为15×30÷18=25（平方米）。

怎么样？有趣的问题是不是有趣地解决了呀？