有趣的搭配
倪艳


小朋友,我们在生话中经常遇到简单的搭配和排列问题,下面让我们一起来探索其中的规律,寻找解决这粪问题的方法。
例1.学校要在3名男生和4名女生中挑选男、女节目主持人各一名,挑选的结果会出现多少种可能?
我是这样解的
可以用字母A1、A2、A3表示3名男生,用B1、B2、B3、B4表示4名女生,用连线的方法寻找问题的答案:
从图中可以看出,先挑选好1名男主持人,再挑选女主持人,挑选的结果就会有4种可能;因为有3名男主持人,所以挑选的结果就有3个4种不同的可能,也就是3×4=12(种)可能。
例2.一列客车在苏州、南京之间往返行驶,中间停靠常州、镇江,每两地之间的距离都不相同,铁路局要印几种火车票?
我是这样解的
先画示意图(如下图),从图中可以看出,从苏州“往”南京,要印火车票3 +2 +1=6(种)。由于“往”和“返”的火车票的始发站和终点站是不同的,例如从苏州去常州与从常州回苏州,虽然票价相同,但却是两种不同的火车票,因此要印的火车票是(3+2+1)x2=12(种)。
例3.用1、2、3、4这四个数字可以组成多少个没有重复数字的三位数?
我是这样解的
按从小到大的顺序思考,百位上是1的三位数有:123、124、132、134、142、143,共6個;百位上是2的三位数有:213、214、231、234、241、243,也是6个;同样,百位上是3和4的三位数也各有6个,因此,一共有6×4=24(个)。
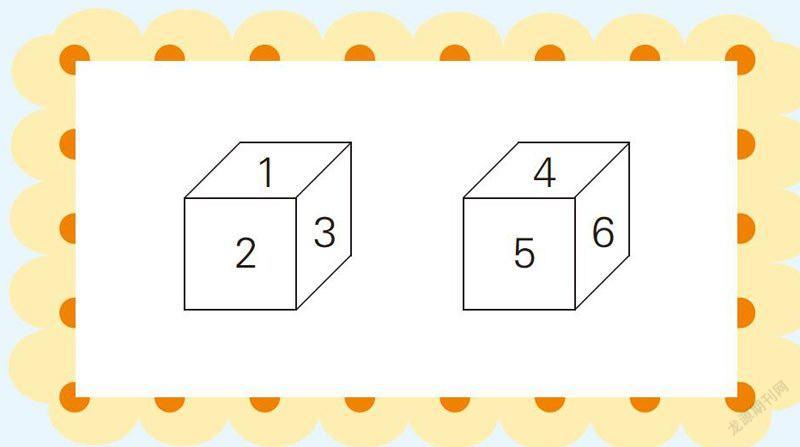
例4.一个骰子的六个面分别写有1-6,如果用两个骰子同时掷(如下图),朝上的两个数相加,一共会出现几种不同的和?和最大是多少?最小是多少?
我是这样解的
可以分步思考,即先确定第1个骰子朝上的数依次为1、2、3、4、5、6,然后依次加上第2个骰子朝上的数,列表如下:
从上表中可以发现,一共会出现11种不同的和,分别是2、3、4、5、6、7、8、9、10、11、12,其中和最大是12,最小是2。
回顾上面的解题过程,我们不难发现,弄清题意,有序思考,不重不漏地列出所有搭配情况,我们就能确定所求问题的答案;画图、列表是解决这类问题的重要策略。

