基于模糊加权马尔科夫模型的晋祠泉域降水预测

王晓敏

（太原市晋祠水利管理处，山西 太原 030024）

大气降水作为晋祠泉域岩溶地下水主要补给来源之一，其降水量的多少对当地岩溶水的开发利用及保护起着决定性作用，因此，建立一个适合该地区降水预测模型是一项十分重要的工作。然而，由于气象条件的多样性、变异性和复杂性，以及降水过程存在着大量的不确定性[1]，使得降水预测的精度难以保证。针对降水的这些特征，许多科研工作者已经开展了许多研究工作，如尤凤春[2]基于奇异谱分析方法，用重建分量对石家庄市的降水进行了趋势预测。孙才志[3]利用山西省河曲水文站50年的降水资料，用加权的马尔科夫链预测了区内未来降水的丰枯变化，并结合模糊集理论中的级别特征值理论，模拟预测了当地未来降水量。葛彩莲[4]基于BP神经网络模型，对青海省10个气象站的降水资料进行了分析预测。根据晋祠泉域的实际情况，并综合考虑各种降水预测方法的特点，对马尔科夫模型进行改进，以期找到一种适合晋祠泉域降水量的预测方法，为晋祠泉域水资源的优化配置和泉水复流提供技术支持。

1 模型简介

马尔科夫过程是一种随机过程，已被广泛应用于随机预报[5-8]，其过程中的“将来”状态只与“现在”的状态有关，与“过去”的状态无关。为弥补马尔科夫过程只重视“现在”及预测结果多直接采用状态划分范围的均值的不足。本次预测运用加权的方法来充分合理利用全部已知信息，运用模糊数学中的级别特征值法求出预测值。模型的具体计算步骤如下：

步骤一：状态分组，利用均值~标准差法对降水序列进行状态划分，具体分级标准见表1。

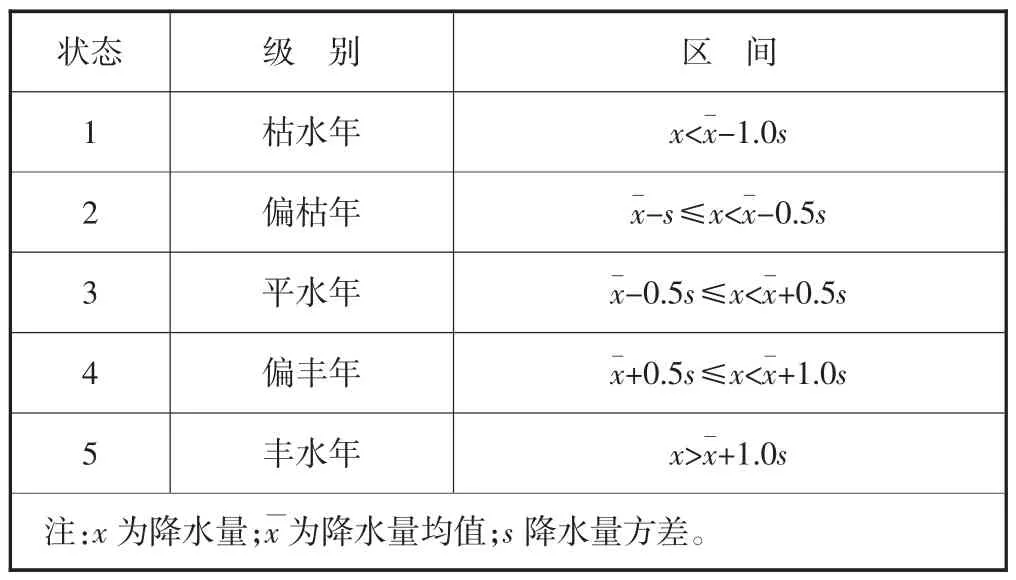
表1 均值标准差法分级标准

步骤二：转移概率矩阵计算，转移概率矩阵是转移频数的矩阵，计算见公式（1）。

式中：Pij为转移概率；fij为第i状态经某步转移为第j状态的频数。

步骤三：马氏性检验，随机序列是否满足马氏性是马尔科夫模型应用的关键，马氏性常用χ2检验法检验。若样本容量足够大，且统计量服从自由度为（m～1）的χ2分布。则给定显著性水平α，当序列统计量为时，随机序列满足马氏性。

步骤四：k阶自相关系数的归一化处理，对降水量序列的各阶自相关系数进行归一化处理，以此作为马尔科夫链不同滞时（步长）的权重，归一化权重因子计算见公式（2）：

式中：rk为k阶自相关系数；xi为第i时段的降水量；为降水量平均值；n为降水序列长度，归一化后的权重因子见公式（3）：

式中：rk为k阶自相关系数；m为预测降水量时需要计算到的最大阶数。

步骤五：n+1时段的状态预测，分别以n+1时段前的若干时段为初始时刻，结合与其相对应的状态转移概率矩阵预测该n+1时段的状态概率，i为状态（i∈（1，2，3，4，5），k为滞时（k=1，2，…，m），预测的同一状态概率进行加权求和作为该状态的预测概率，即pi=预测概率最大状态的即为n+1时段的状态。

步骤六：降水量预测，利用模糊集理论中的级别特征值法将降水状态预测中得到的区间值具体到一个数值。首先根据公式（4）计算各状态的权重，并将计算出的5个权重构成权重集D={d1，d2，d3，d4，d5}。

式中：η为最大概率作用系数，其值通常取2或4，本次计算取2。

为级别特征值。则预测值见公式（5）。

式中：i是确定的所预测概率最大的状态，Ti和Bi分别是i状态下的上下限值。

在预测时，需将预测值放入原序列，重复第二到六步骤。

2 模型计算

2.1 模型的模拟检验

晋祠泉域面积2030 km2，是山西省19个岩溶大泉之一，泉域多年平均降水量为463.6 mm。根据泉域1956年—2011年的降水资料，利用改进的马尔科夫模型（模糊加权马尔科夫模型）进行模型计算，并对晋祠泉域2012及2013年的降水量进行模型检验。计算步骤及结果如下。

晋祠泉域降水状态划分，通过计算降水量的均值及无偏估计标准标准差，对照表1进行年降水的降水状态划分，结果见表2。

转移概率矩阵计算，以1956年—2011年的状态转移频数，计算的1—5步长的状态转移概率矩阵结果如下。

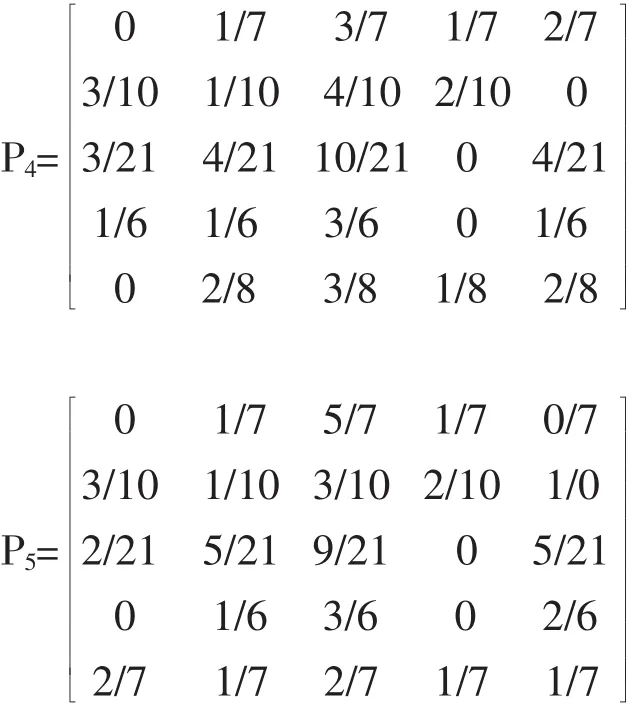
马氏性检验，根据χ2检验，χ2=36.22＞χ20.05（16）=26.3，可知晋祠泉域的年降水量序列满足马氏性。

晋祠泉域降水序列的各阶自相关系数和权重值，降水自相关系数r1=－0.239，r2=0.141，r3=0.125，r4=－0.021，r5=－0.017，各阶自相关系数归一化后作为的滞时权重为w1=0.438，w2=0.259，w3=0.229，w4=0.040，w5=0.032。

降水量预测，根据2007年—2011年的降水量及其相对应的状态转移概率矩阵，预测出的2012年降水量状态预测概率见表3。

表3 2012年降水量状态预测概率

由表3可知，i=3时，Pi=0.427时值最大，说明预测的2012年为平水年的可能性最大。

利用模糊集理论中的级别特征值法计算得2012年的降水量级别特征值为2.798＜3，所以P2012=BiH/（i+0.5）=458.005，实际值为499.9，残差为41.895，相对误差为8.38%。运用同样的方法重复步骤2～5，计算得2013年i=3时，Pi=0.349时的值最大，说明预测2013年同样最有可能为平水年，2013年的级别特征值为3.418＞3，所以P2013=TiH/（i+0.5）=531.318，实际值为527.9，残差为3.418，相对误差为0.65%（见表4）。

由表4可知，模糊加权马尔科夫模型在晋祠泉域预测的降水量相对误差在10%以内，满足水文预报中

表4 模型检验

大于20%的误差要求[8]，所以可以利用模糊加权马尔科夫模型对晋祠泉域的降水量进行预测。

2.2 降水量预测

利用晋祠泉域1956年—2013年的降水资料，重复2.1中的2～5步骤，最终预测出的2014年—2020年的降水量见表5及图1。

表5 2014年—2020年降水量预测

图1 晋祠泉域降水量预测结果

由表5及图1的预测结果可知，晋祠泉域2014年—2020年的降水量范围在451.66～480.81 mm之间，最大相差29.2 mm，平均值为460.86 mm。降水量总体的趋势较平稳，预测年份均属于平水年。

3 结语

基于模糊加权马尔科夫模型对晋祠泉域的降水量进行了模拟预测，结果表明改进的马尔科夫模型对晋祠泉域的降水量模拟效果较好，该方法可作为晋祠泉域降水量预测模型，为泉域的水资源开发利用规划及水资源管理提供技术支持。本模型有待改进的是均值～标准差法确定的降水状态划分标准，范围仍有些偏大，在一定程度上影响了模型模拟预测的精度，是今后需要进一步研究的问题。

［1］王文科，廖健榕.模糊分析在水文地质学中的应用［M］.西安：西安地图出版社，1997：1-3.

［2］尤凤春，史印山，周煜.奇异谱分析方法在夏季降水预测中的应用［J］.气象，2002，28(11)：22-25.

［3］孙才志，林学钰.降水预测的模糊权马尔可夫模型及应用［J］.系统工程学报，2003，18（04）：294-299.

［4］葛彩莲等，蔡焕杰，王健等.基于BP神经网络的降水量预测研究［J］.节水灌溉，2010（11）：7-10.

［5］冯耀龙，韩文秀.加权马尔可夫链在河流丰枯状况预测中的应用［J］.系统工程理论与实践，1999，19（10）：89-93.

［6］Sen Zekai.Critical drought analysis by second-order Markovorder［J］.Journal of Hydrology，1990，120（4）：183-202.

［7］王文圣，丁晶，金菊良等.随机水文学（第二版）［M］.北京：中国水利水电出版社，2008：20-23.

［8］水利部水文局.GB/T 22482-2008水文情报预报规范［S］.北京：中国标准出版社，2008.