斜拉桥钢索模型的双曲型偏微分方程数值解及Matlab实现
杨树林
(中国石油大学胜利学院 教学科研处,山东 东营 257061)
斜拉桥在桥梁工程领域应用广泛,越来越多地出现在江河之上,但仍有许多问题有待进一步探索。例如,斜拉桥常用张紧的钢索来进行承载、运输和牵引等作业,而钢索在运营过程中张力会发生改变,导致受力不均,从而影响整个斜拉桥的质量。因此,对斜拉桥钢索模型进行模拟,确定其主要影响因素,对于工程设施运行的安全和行人的人身安全至关重要。较之前人对斜拉桥钢索模型进行的研究,笔者从弦振动的基本理论出发通过建立相应的双曲型偏微分方程初边值问题的新模型对斜拉桥钢索问题进行深入探讨。
1 模型假设
(1)假设斜拉桥钢索的质量均匀分布;
(2)假设斜拉桥钢索上每一小段只有“横振动”,即振动发生在一个平面内,且各点的运动方向垂直于平衡位置;
(3)假设斜拉桥钢索振动的幅度及任意点切线的倾角都很小;
(4)假设斜拉桥钢索的初始位移方程接近悬链线方程[1]。
2 模型建立
考虑到斜拉桥钢索平衡时沿直线拉紧,除受不随时间变化的张力和弦本身的重力作用外,不受其它外力影响[2],可得定解问题为
(1)
式中,弦上横坐标为x的点在时刻t的振动位移为u,斜拉桥钢索两端分别固定在x=0及x=l处,q=H/ρg为悬链系数,与斜拉桥本身的特质有关,H为斜拉桥每一点处张力的水平分量[3]。
3 模型求解
用第n-1层,n层,n+1层的中心差商的加权平均去逼近uxx,得到逼近微分方程(1)的差分格式如下:
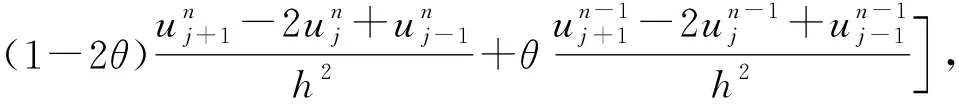
(2)
其中0≤θ≤1为参数[4]。
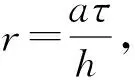
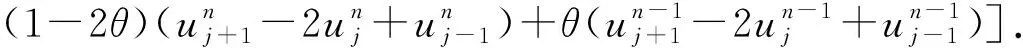
(3)
移项整理得
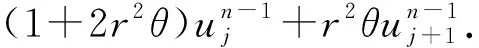
(4)
这是一个三层格式,先将其转化成两层差分方程组:
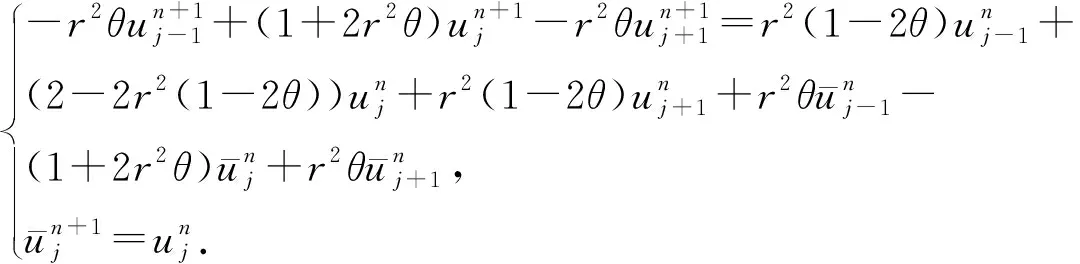
(5)
写成矩阵形式:
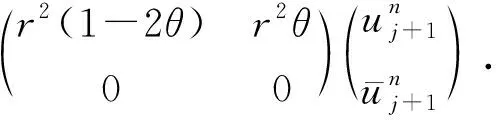
(6)
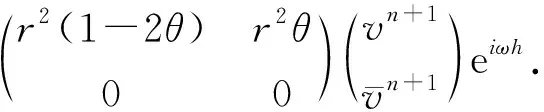
(7)
即
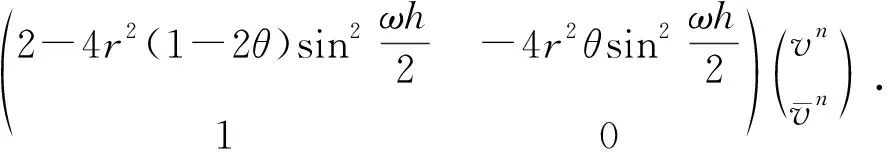
(8)
整理得
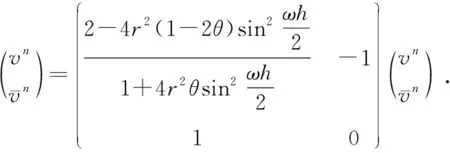
(9)
过渡矩阵为
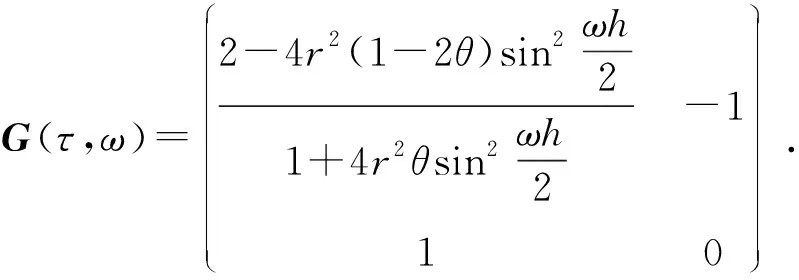
(10)
特征方程为
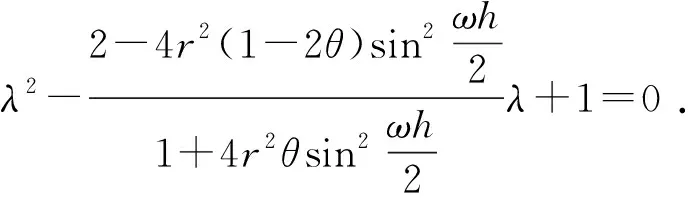
(11)
方程ρ2-2bρ+1=0的根按模不大于1的充要条件为|b|≤1。
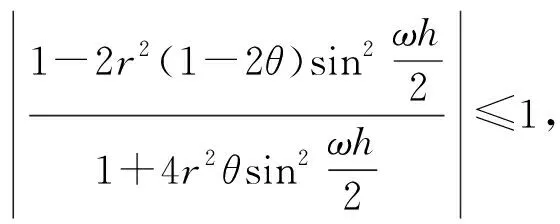
将θ=0代入式(2),则
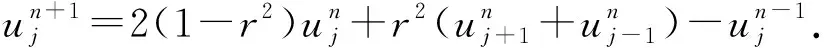
(12)
该式为显式格式。此格式具有二阶精度,截断误差为:
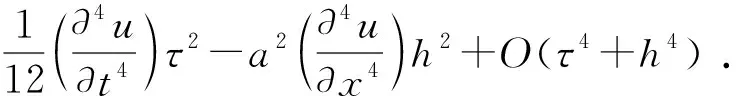
(13)
阶为O(τ2+h2),在时间步长τ和空间步长h都趋于零时,差分方程的截断误差也趋于零, 差分格式(12)是相容的。
通过对稳定性、相容性的讨论知,差分格式(4)是收敛的,能够通过该差分格式求得偏微分方程(1)的近似解,对式(4)结合相应的离散化的初边值条件
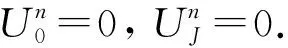
(14)
可形成三对角方程组,采用追赶法求解[5]。
4 结果分析
利用Matlab语言对不同条件下的数值解进行求解[6],令q=100,通过对两种方案——θ变化,网格比不变;θ不变,网格比改变的运行结果进行分析得出在一定范围内,当网格比不变时,θ越小图形越平缓,数值解误差越小,模拟程度越好;当θ不变(即对于同一种差分格式),网格比增大时,数值解误差增大,误差阶也增大,模拟度越低。如图1和2的试验结果所示。

图1 θ变化,网格比不变的运行结果
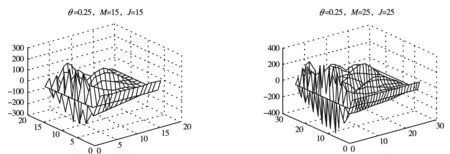
图2 θ不变,网格比改变的运行结果
5 结束语
从弦振动的基本理论出发,研究了斜拉桥钢索问题,在对斜拉桥钢索进行适当假设的基础上,导出了其不受外力作用时的振动方程,并用分离变量法求出了其满足定解条件的精确解,讨论了固有值λ<0、λ=0和λ>0三种情况下,固有值常微分方程问题的通解。对弦振动方程而言,当方程与边界条件均为齐次时,不管初始条件如何,可直接用分离变量法求解,并运用matlab语言对差分方程的数值解进行分析,最后通过将不同条件下的数值解进行比较确定该模型的模拟程度。在一定范围内当网格比不变时,θ减小时,数值解误差减小;当θ不变(即对于同一种差分格式),网格比增大时,数值解误差增大,误差阶也增大。该模型为模拟斜拉桥钢索模型提供了一种较为合理的方法,能够广泛应用于实际生产生活的各个领域,如弹性杆的纵振动、管道中气体小扰动的传播、空中缆车钢索问题等,借助于matlab软件进行数据拟合,绘出的图像能够更好地验证数值求解结果的正确性。

