调剖最优处理半径计算方法研究及应用
王 涛,刘文锐,王艳红
(1.中海油田服务股份有限公司 油田生产事业部,天津 300459; 2.中国石油吐哈油田 勘探开发研究院,新疆 哈密 839009)
调剖作业时,如果调剖剂用量少,可能达不到措施预期效果;如果处理剂用量过大,则会造成药剂浪费,增加施工成本。因此,最优调剖半径的确定至关重要。目前,化学调剖封堵半径的确定方法主要有以下几种方法:一是通过达西公式推导出的计算公式[1-3],此方法假定地层均质且无限大,根据调剖前后预期的吸水能力比值以及残余阻力系数确定处理半径,但实际地层往往非均质性比较强,且也不是无限大,计算结果与实际相差很大;二是依靠工艺人员的现场施工经验确定,主观随意性强;三是根据室内试验统计得到经验半径[4],虽然具有一定的指导意义,但是具体区块需做具体试验分析,耗费精力财力。为快速准确计算调剖最优处理半径,本文从非活塞式水驱油的渗流理论出发,推导出计算最佳封堵半径的计算公式,并编制了相应的计算程序。该方法主要基于油藏动静态资料,具有简便快捷、精确度高的特点,实例计算结果表明其对水井调剖具有较好的指导意义。
1 计算模型的建立
建立两层的一注一采水驱理论地质模型,第1层设为低渗且动用较差层,第2层设为高渗水窜层,可由达西公式推导出每层的吸水量:
式中,k为渗透率,10-3μm2;h为油层厚度,m;Q为吸水量,m3/d;h1为低渗透层厚度,m;h2为高渗透层厚度,m。
注水井调剖作业目的是注入化学药剂将高渗层进行封堵,延缓高渗层见水,使高低渗层水驱前缘同步均匀前进,假设封堵长度为L1,分以下两种情况进行研究分析:
(1)当L1≤X0时(图1),注水量Q将均匀推进L1的距离,然后产生分流。由非活塞式水驱油理论计算可得高渗层的见水时间:
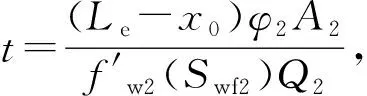
(1)
A2=bh2.
(2)
在时间t内低渗层的水驱油前缘位置[5]:
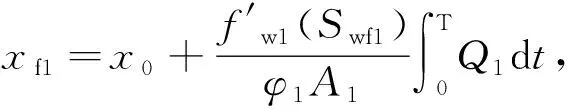
(3)
A1=Bh1.
(4)
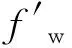
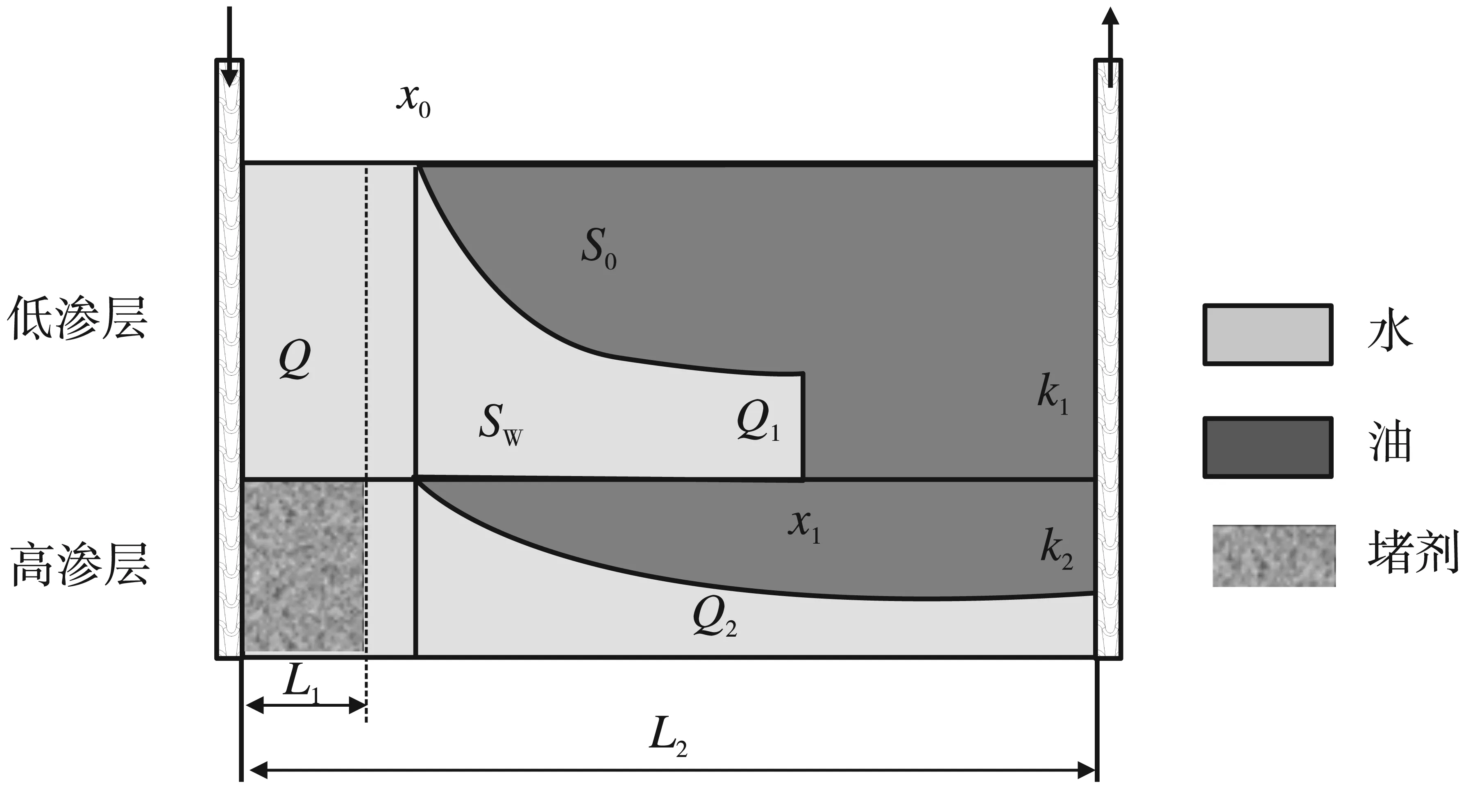
图1 调驱封堵模型(L1≤X0)
由式(1)和式(3)可以看出,当L1≤X0时,高渗层的封堵距离L1并不影响低渗层水驱前缘的波及距离。
2)当L1>x0时(图2),注入水将均匀推进至x0处,然后进入两相区。水驱油前缘至L1的位置,其水柱高度为hw,含水饱和度为Sw,含水率为fw。
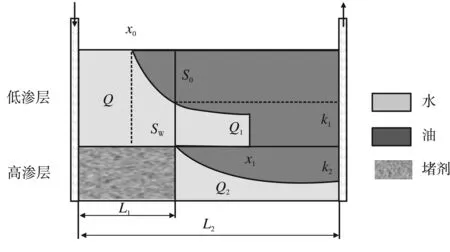
图2 调驱封堵模型(L1>x0)
水驱油前缘过了L1后,将分流为Q1和Q2。当高渗层见水时,所需时间:
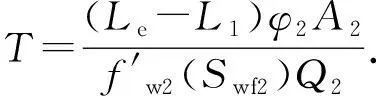
(5)
此时低渗层水驱前缘的位置x1为:
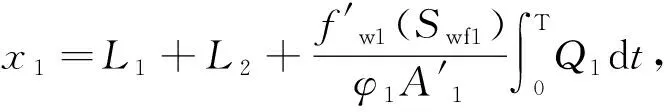
(6)
式中,L2为低渗透层水驱前缘分流前超出封堵半径L1向前运行的距离。
从式(6)可以看出,当高渗层封堵半径越大时,低渗层水驱波及的距离就越远。高渗层的最佳封堵半径是指使得低渗层水驱油前缘刚好到达井排时的封堵半径,也即高低渗层同时见水。此时,x1=Le,即得最佳封堵半径Lc:
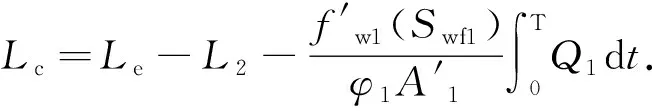
(7)
2 计算实例
2.1 高低渗层的模糊评判
以某油田A注水井为例,开展调剖最佳封堵半径的计算研究,A井目前注水量是507 m3/d,吸水剖面如图3所示,各小层吸水量计算公式为:
Qi=Qwi.
式中,Q为注水总量;wi为各小层吸水量占总注水量的比值。
应用以上公式求得各小层的吸水量,同时统计各小层厚度、孔隙度、渗透率等物性参数统计见表1。
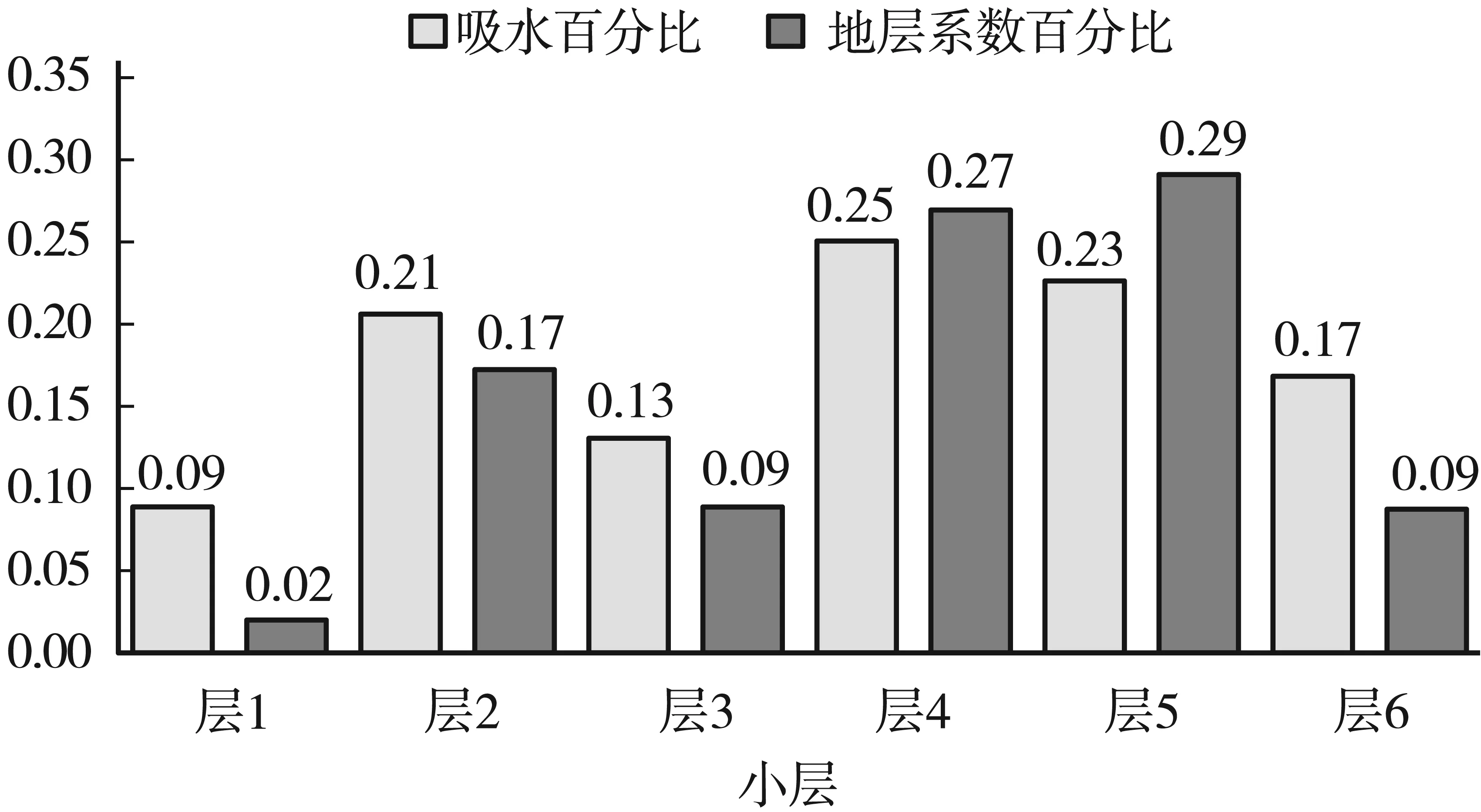
图3 A井吸水剖面图
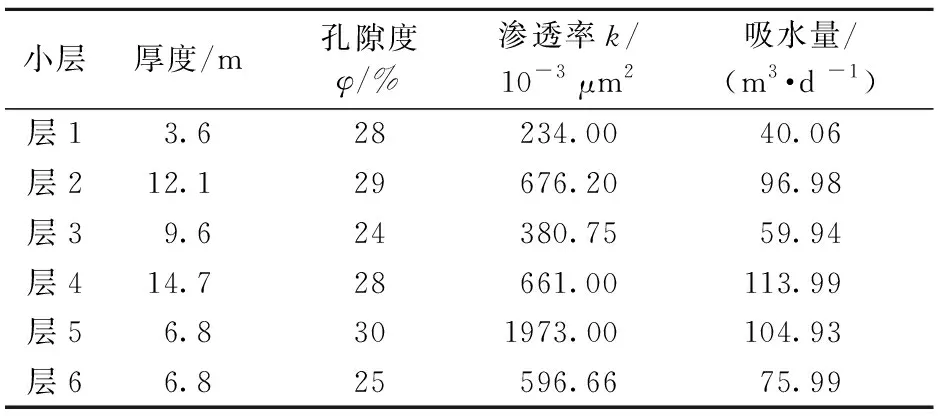
小层厚度/m孔隙度φ/%渗透率k/10-3 μm2吸水量/(m3·d -1) 层13.628234.0040.06 层212.129676.2096.98 层39.624380.7559.94 层414.728661.00113.99 层56.8301973.00104.93 层66.825596.6675.99
油田实际注水井大都是多层笼统注水,而并不是仅有高渗和低渗两层,因此采取模糊数学隶属函数的半梯形分布法[6-7]对小层厚度、孔隙度、渗透率、吸水量隶属对进行计算后,将吸水层进行高低渗透层划分评判度,评价结果见表2、表3。
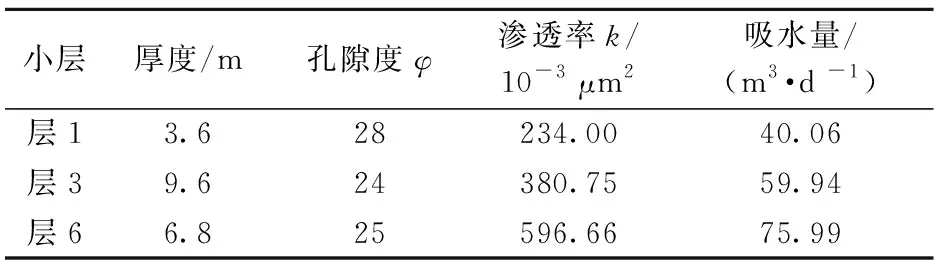
表2 A井低渗层物性参数及吸水量统计
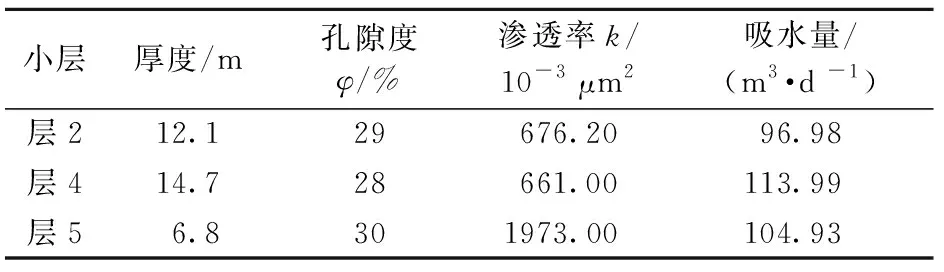
表3 A井高渗层物性参数及吸水量统计
2.2 最佳处理半径计算结果
在对高低渗层评判划分后,进行矿场实例计算,调驱井距选取A井周围一线受效井平均井距287 m,应用式(7)数学模型编写计算程序,计算得到最佳封堵半径为49.6 m(图4),之后便可针对具体调剖药剂计算出药剂总量。由此可以看出运用此方法,结合目标井的动静态参数可以快速准确得出最佳调驱半径,对现场施工设计具有较高的应用价值。
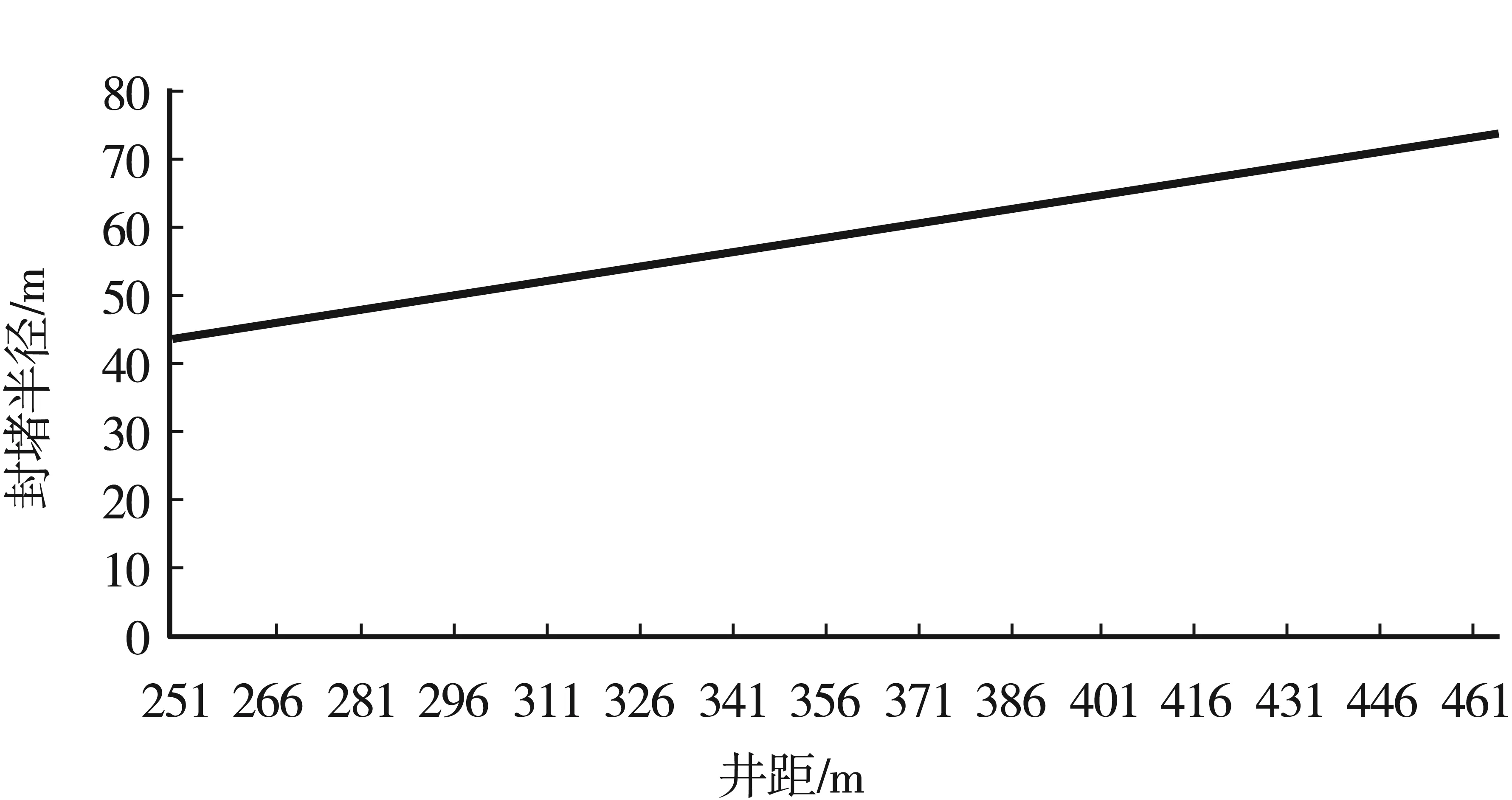
图4 A井不同井距下最佳封堵半径曲线
3 结 论
(1)综合考虑油藏动静态资料,通过模糊评判法将目标井划分为高低渗层进行计算,可有效应用于多层大段合注井调剖半径计算。
(2)公式现场应用简便快捷,计算精确度高,封堵半径计算结果一般为井距的0.15~0.2,与室内试验一致。实例应用也进一步表明其对水井调剖施工具有较好的指导意义。
——以吉木萨尔芦草沟组为例

