经历探究过程 积累活动经验—以《条形统计图》教学为例

许丽荔

（福建省莆田市荔城区梅峰小学，福建莆田　351100）

引　言

《义务教育数学课程标准》（2011年版）倡导要让学生经历知识的形成过程。学生的学习过程是一个再创造的过程。有些知识模型是可以由学生进行再创造的，这就要求学生要清楚知识发生、发展的过程[1]。因此，教学中，教师要让学生通过“做”数学、“玩”数学经历数学知识的形成过程。数学思想也必须通过“再发现”的方式让学生习得，将教学活动中蕴含的数学思想方法充分“释放”。下面以四年级上册的《条形统计图》为例，谈谈如何让学生经历探究过程，树立数据分析观念，感悟数学思想与方法，积累数学活动经验，从而提升核心素养。

一、优化整合教材，利于学生经历过程

《义务教育数学课程标准》中指出：教学内容的选择要贴近学生的实际，有利于学生体验与理解、思考与探索课程内容的组织；课程内容的组织要重视过程，处理好过程与结果的关系。

要实现课堂数学的有效、实效、高效，必然要求教师善于结合实际教学的需要，灵活地、有创造性地使用教材，对教材的内容、编排顺序、教学方法等方面进行适当的取舍或调整，使之更加有利于学生主动自觉地投入学习，更加有利于学生经历知识发生、发展的过程，以期实现在有限的时间内使学生能力与知识兼顾，容量与质量并进的目的，在有限的时间里取得最好的教学效果，从而实现教学过程的最优化。同时，教师创造性地使用教材的过程也是帮助教师自我提升、自我完善的过程。

《条形统计图》这一课属于统计与概率领域。对于这一内容，教材安排了三个例题，分为三个课时来上。例1是用一个格表示一个单位的条形统计图，例2和例3是分别学习一个格表示多个单位的条形统计图。为了利于学生的思维发展，可以把三课时的内容优化整合成两个课时：第一课时是把例1、例2、例3整合在同一课时上，第二课时再上相关内容的练习课。把三个不同内容的例题都改成研究喜欢课外书籍情况的例题：

例1四（1）班女生最喜欢的一种课外书籍情况，统计如下：

例2四（1）班学生最喜欢的一种课外书籍情况，统计如下：

例3四年段学生最喜欢的一种课外书籍情况，统计如下：

书籍种类　童话故事　科普读物　儿童文学　漫画书人数（人）　80　100　96　60

这样的设计，既省时高效，又利于学生经历数据分析的整个过程。

二、经历过程，感悟数学思想，积累数学活动经验

数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括。学生在积极参与教学活动的过程中通过独立思考、合作交流，逐步感悟数学思想。

如何在《条形统计图》一课中让学生经历探究过程，树立数据分析观念，渗透数学思想，积累数学活动经验呢？教学中，教师可引导学生经历以下几个活动过程：

活动1 ，先出示表1：

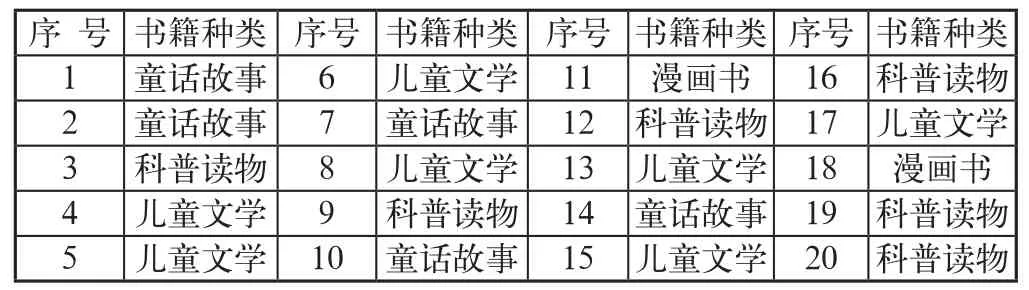
表1　每种书籍喜欢的人数统计

你能从这个表格一眼看出来每种书籍喜欢的人数吗？你想怎么做？统计好数据用什么方法清楚表示出来？选择一种你喜欢的方法来表示每种书籍喜欢的人数。有的学生用统计表，有的学生用象形图，有的学生用条形统计图……

让学生经历收集数据、整理数据的过程，感悟整理数据形式的多样化。

活动2，认识条形统计图（图1）。横轴表示什么？为什么要在纵轴标上数据？这些数据表示什么？纵轴上的每一格表示多少？你能从这个条形统计图中，获得哪些信息？

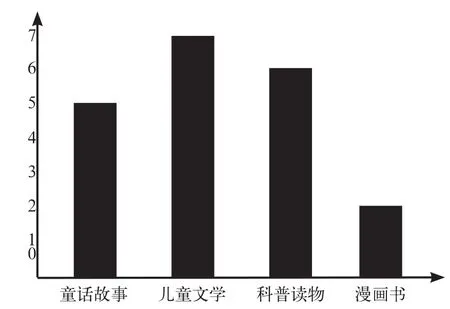
图1

在这个活动中，学生了解条形统计图的基本结构，掌握构成条形统计图整体的完整性的必备条件，感悟纵轴数据的重要性，会用数据分析一些简单的问题，建立分析数据的意识。

活动3，比较统计表、象形图、统计图。这三种方法，有什么相同的地方？（都表示书籍喜欢情况，都有项目、数据）对数据的表示哪种更直观、形象？（条形统计图）在比较中进一步体会条形统计图的特点与优点。渗透比较、优化、不变中抓变化（不变的是数据，变的是对数据的表现形式），以及数形结合等数学思想。

活动4，出示例2，这是全班同学最喜欢的一种课外书籍情况统计表。在完成统计图的活动中，教师提问：现在每小格还能用1来表示吗？让学生感悟数据变了，纵轴每一小格表示的数据也要跟着发生变化，再次感受到统计图纵轴数据的重要性。

活动5，拓展想象，总结提升：根据上面的女生和全班学生两种最喜欢书籍统计情况，预测一下本校四年级所有同学最喜欢的书籍是什么情况？你还能预测什么？感受统计具有预测功能，体会到分析数据能帮助人们做出决策。再出示例3：四年段全体同学最喜欢的一种书籍情况，接着出示全校同学最喜欢的一种书籍情况。那么继续往下想象，如果是全区，你会做吗？思考一下，无论怎么变……通过三个统计图加上想象来归纳，学生深刻体会，不管数据怎样变化，变的是纵轴每格表示数的大小，而统计图的基本结构是不变的。这渗透了变中抓不变的数学思想。学生经历这样深刻的体验过程，突破纵轴的数据怎样标这个难点，发展了想象能力。最后让学生说说还见过哪些条形统计图，并在欣赏条形统计图的过程中体会学习统计图的必要性。

学生经历了这样几个活动过程，对知识的掌握是入心入骨的，落实了四基（基础知识、基本技能、基本思想、基本活动经验），发展了四能（发现问题的能力、提出问题的能力、分析问题的能力、解决问题的能力），积累了数学活动经验，提升了数学核心素养。

结　语

实践证明，学生只有经历过程，知识的学习才是牢固的，数学思想的感悟才是深刻的，经验的积累才是丰富的。