浅海远程混响与目标回波融合仿真方法研究
王升 刘熙沐 裴秋秋 靖树一
(中国人民解放军91388部队,湛江, 524022)
浅海环境中,界面及水体散射形成的混响是主动声呐的主要干扰,限制了水下跟踪探测的作用距离,提高了主动声呐虚警概率。混响和目标回波信号特征的分析是抑制混响的基础,海上实验是获取信号特征的直接手段,然而受到各方面条件的制约不可能经常进行,信号仿真可以作为替代手段为声呐设计和信号处理方法研究提供参考数据。国内外学者对浅海远程混响的研究进行了大量研究[1-3],基本方法是借助简正波理论计算声传播过程,在海底附近将简正波分解为上行波和下行波(本征函数展开法),结合海底散射函数得到海底散射场,再结合发射信号强度及脉宽等参数可以进一步计算混响强度和混响序列。
波导中目标散射问题与海底微元散射类似,主要区别在于散射函数,可以采用相同方法研究,文献[4,5]利用本征函数展开法系统地研究了波导中目标散射问题,并且提出了模式匹配(Matched-mode processing)目标定位方法和目标散射函数反演方法。文献[6]将目标回波看作发射信号与目标散射声场的卷积,给出了浅海波导中目标回波波形的具体算法。
从形成机理上混响和目标回波都属于海洋中声散射问题,区别只在于目标散射特性,因此,可以借助成熟的简正波理论进行混响和目标回波信号的融合仿真。本文在前人研究的基础上,首先给出统一形式的海底微元和目标散射场,然后结合源信号频谱作傅里叶变换获得了混响背景下的目标回波仿真波形。文章以刚性球为例对Pekeris环境下的混响和目标回波进行了仿真及垂直相关性分析,通过对仿真信号作波束形成验证了垂直线阵波束形成抑制海底混响的可行性。
1 海底微元和水中目标的散射场
浅海波导中单频点源条件下的目标稳态散射场的计算是目标回波信号仿真的基础。采用简正波方法研究混响和目标散射场的主要难点是如何将传播过程与散射过程联系起来,依据“射线-简正波”类比理论[7],简正波在目标或海底附近可以分解为准平面波形式,这样就可以利用目标的平面波散射函数得到简正波耦合矩阵,结合传播过程给出海底微元和目标散射声场,如图1所示。
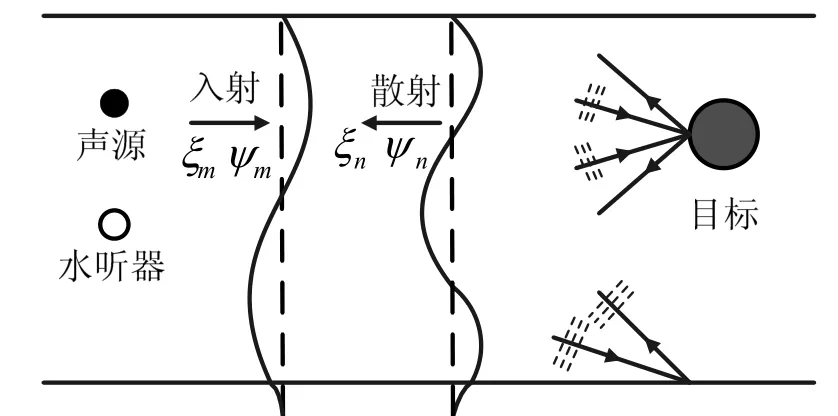
图1 混响和目标回波的简正波方法示意图
借助上述方法,文献[1]推导出的海底微元散射场和文献[5]给出的目标散射场计算公式具有相似结构:
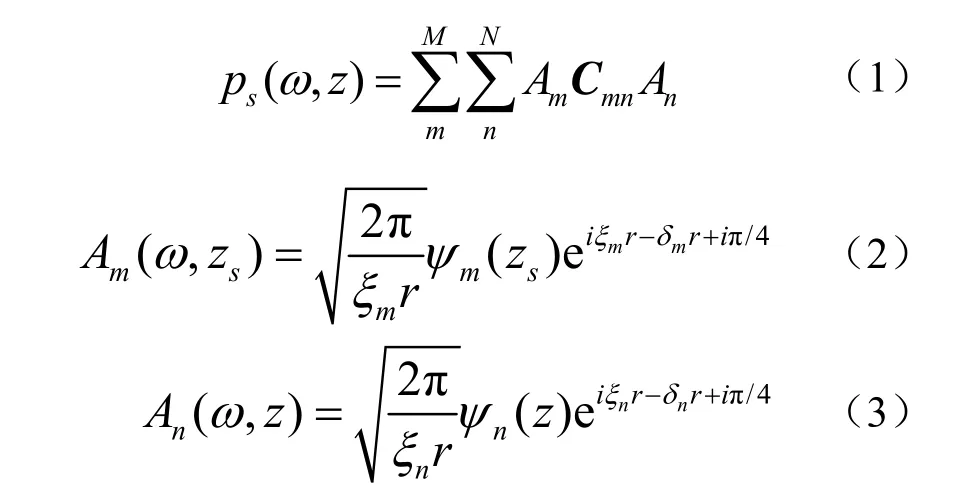
式中,Am为入射声场,An为散射声场,m、n分别为入射简正波和散射简正波的标号,ω为声场角频率,ξm、ψm分别是第m号简正波的本征值和本征函数,δm是对应的衰减系数,z、zs分别是接收点和声源深度,收发合置情况下r是声源到目标的水平距离,Cmn为反向散射耦合矩阵。
可以看出,海底微元和目标散射场的计算皆分为传播过程和散射过程,传播过程相同,为波导中的声传播,不同之处是散射耦合矩阵。海底微元散射简正波耦合矩阵为:
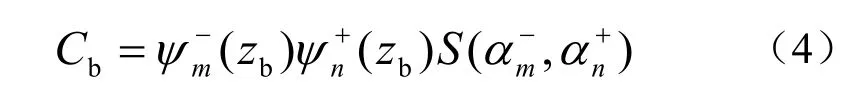
目标散射简正波耦合矩阵[5]为:
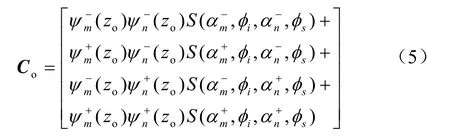
2 混响和目标回波融合仿真方法
在海底散射体真实分布情况未知的条件下常采用单元散射模型来计算海底散射场,即认为海底由许多均匀分布的海底微元组成,每个微元的散射特性由经验函数描述,与面积成正比。实际情况下,发射信号通常为时宽受限的脉冲信号。对于收发合置情况,对t时刻混响有贡献的海底散射区域为圆环,圆环内半径为cu×t/2,外半径为cu×(t+τ)/2,cu为平均群速度,τ为源信号脉宽;假设待仿真混响序列的时间窗口为[t1,t2],则对窗口内混响序列有贡献的海底区域为内径cu×t1/2、外径cu×(t2+τ)/2的圆环。海底散射场是由对设定时间窗口内混响序列有贡献的所有海底微元散射场叠加而成[3]:
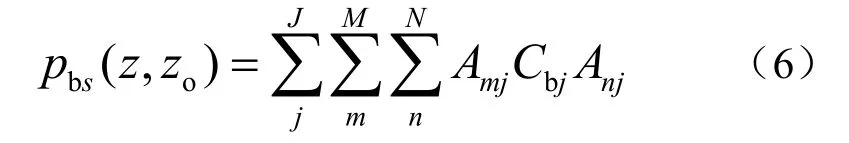
其中,pbs表示海底散射场,j是散射微元的编号,J表示对时间窗口内混响信号有贡献的散射微元总数。仿真计算时可以将海底有效区域分为多个等宽度的圆环带,认为圆环带内微元到声源距离相同,每个圆环带又分为多个微元,每个微元面积与波长呈正比,考虑到海底微元位置和散射幅度的随机性,应为耦合矩阵Cbj加随机相位和幅度。
不考虑目标散射场和海底散射场的相互影响,混响背景下目标散射场可以表示为:
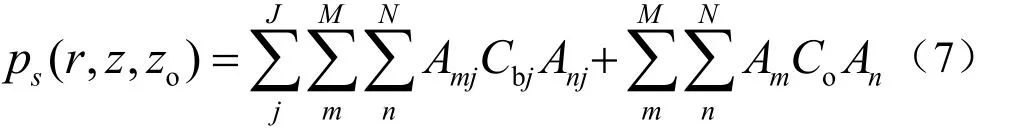
将声波在海洋信道中传播及目标散射过程视为一个传输网络,单频点源散射声场可以作为谐波信号作用于传输网络形成的传输函数,结合源信号频谱作逆傅里叶变换,可获得混响背景下目标回波信号的时域波形:
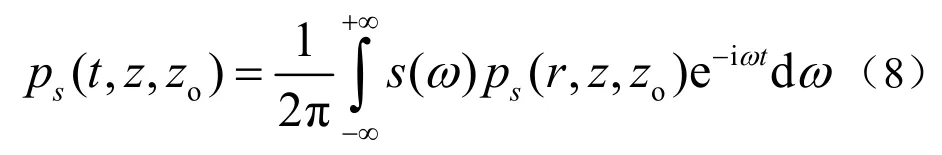
3 仿真分析
3.1 信号仿真
水下目标设为理想刚性球,半径10 m,其散射函数[6]为:
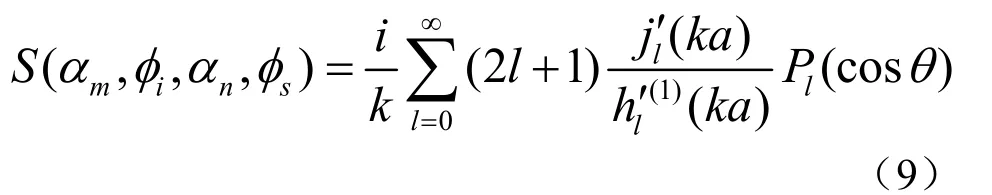
其中,k为目标处的波数,a为刚性球半径,θ为入射波和散射波的夹角,是宗量为cosθ的第l阶勒让德函数,是宗量为kr的第l阶第1类球汉克尔函数,是宗量为kr的第l阶球贝塞尔函数。
海底散射强度是混响信号仿真中的一个重要参数,决定了混响信号中各号简正波的能量分布。海底散射特性通常采用经验统计模型来描述,本文采用 Lambert定律[1],海底微元dAj的声压散射函数为:
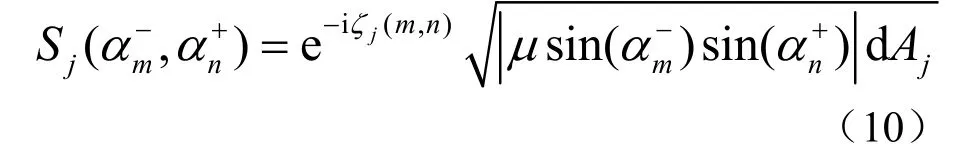
其中,海底散射系数μ满足10lgμ=−27 dB,ζj为随机相位,在[0,2π]之间均匀分布。
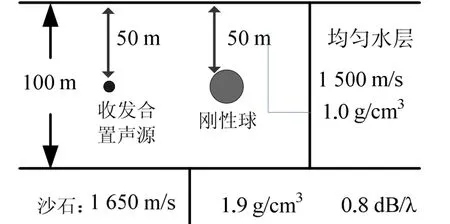
图2 环境参数和目标、发射接收位置示意图
海洋环境相关参数如图2,水平分层海洋环境,海底为沙石底质,粗糙度均匀且各向同性。声源为200 dB点源,发射信号为LFM信号,载频300 Hz,调频宽度50 Hz,脉宽0.5 s。简正波本征值和本征函数借助 KRAKEN程序计算。混响信号采样时间从0.3 s开始至10.3 s结束,采样率2 400 Hz;设定每个圆环带宽度15 m,每个微元面积5 m2。当目标与接收点距离分别为2 km、4 km、6 km时,仿真结果如图3所示。
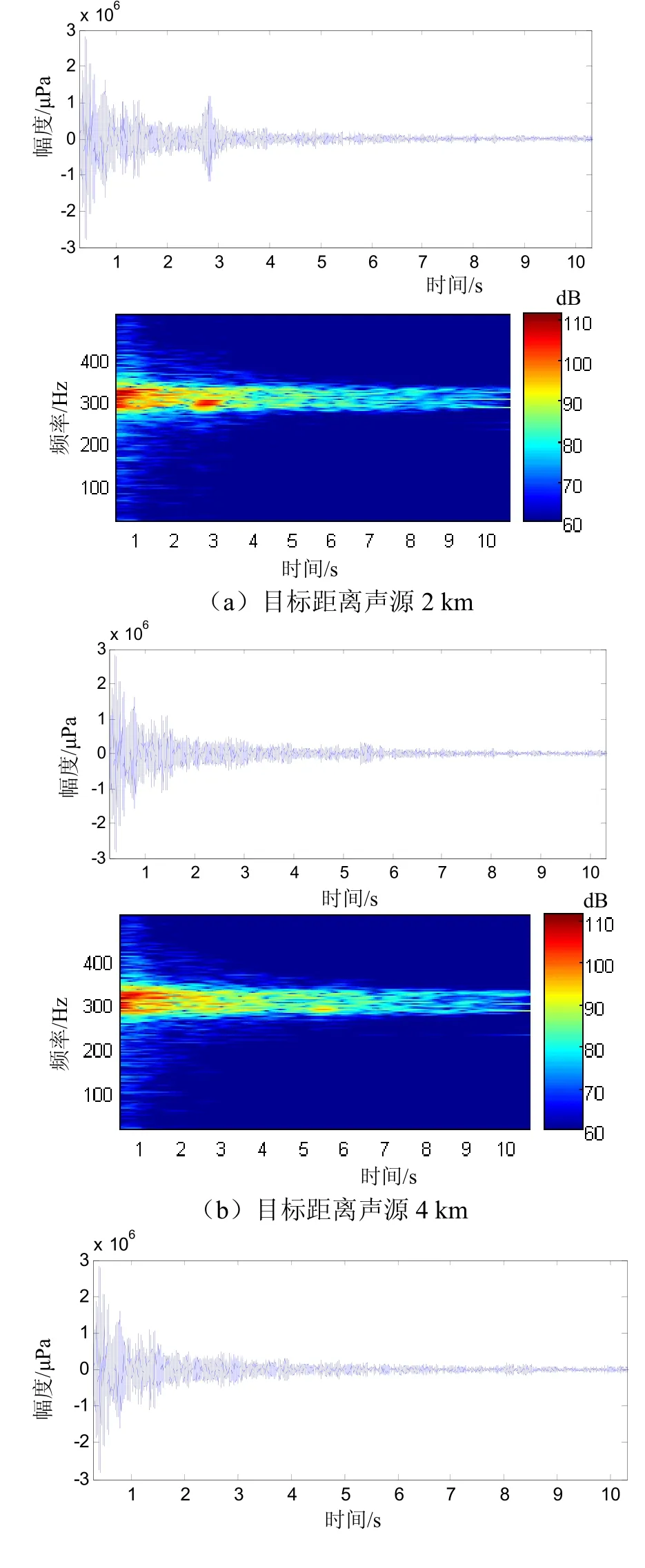
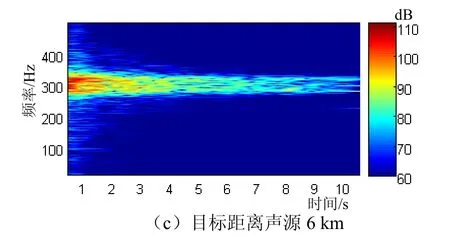
图3 混响和目标回波融合仿真结果
3.2 仿真混响序列统计特征
文献[8]中混响信号的统计特征应满足以下规律:(1)不考虑声呐和散射体之间的相对运动时,混响信号应与源信号频谱相一致;(2)混响信号的瞬时幅值服从高斯分布,而包络幅值服从瑞利分布;(3)混响信号的时间相关半径与带宽成反比。
图4为上一节仿真混响信号的频谱与发射信号频谱的比较;图5和图6分别为混响信号的瞬时值概率密度和包络值概率密度;图7为不同带宽的混响信号的自相关函数。可以看出:仿真混响序列的自相关半径与带宽成反比,仿真信号的频谱特征和统计特征也都符合理论预测。
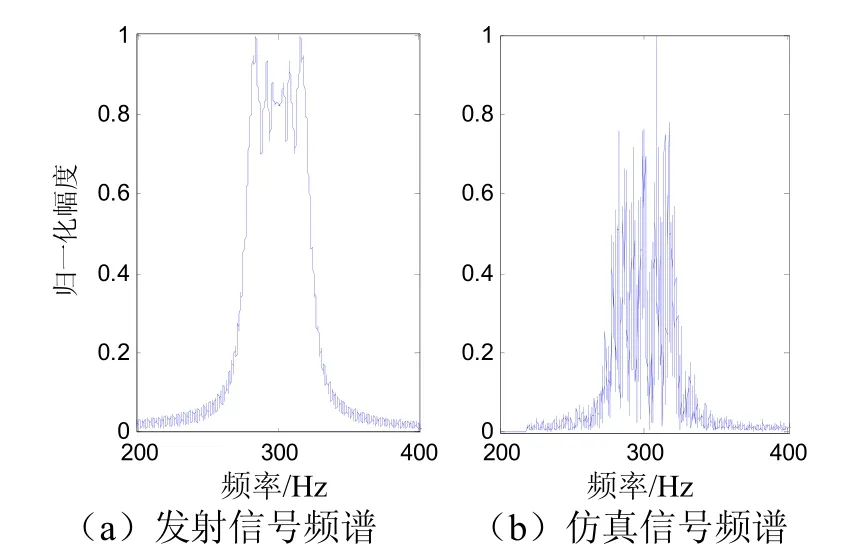
图4 发射信号与仿真信号频谱比较
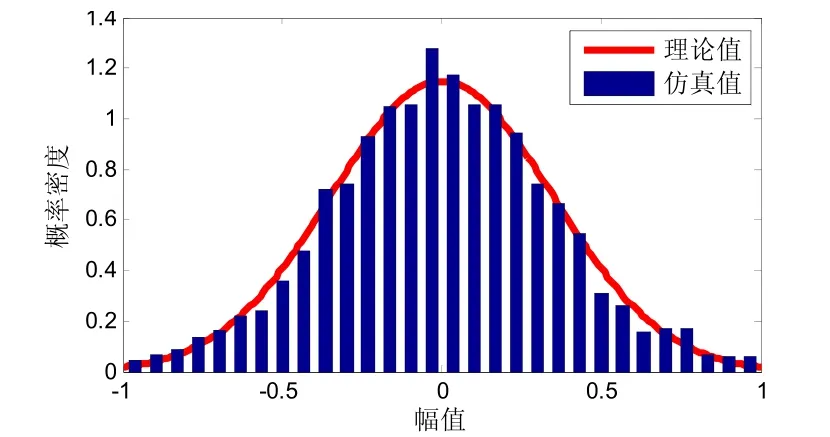
图5 瞬时概率密度(均值μ=0,均方差σ=0.35)
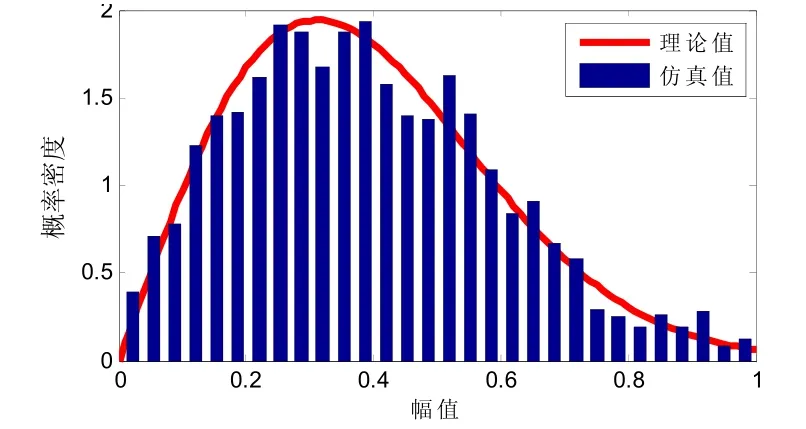
图6 包络概率密度(均方差σ=0.20)
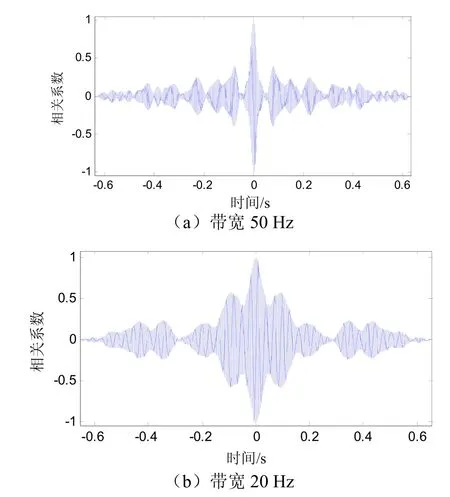
图7 仿真混响信号的自相关函数
浅海混响在垂直方向上有很强的相关性,文献[9]认为垂直相关系数随时间增加而增大。图8为50 m与55 m两个深度上接收混响的互相关系数,随时间而逐渐增大,符合理论预测。这是由于弱垂直相关性的高号简正波传播衰减较快而导致的。
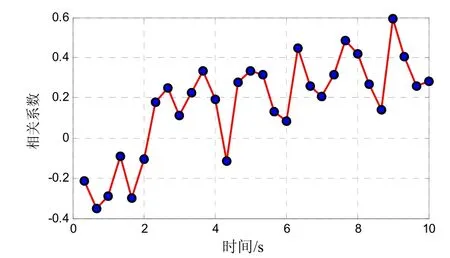
图8 混响垂直相关系数随时间的变化
3.3 混响和目标回波的垂直相关性
信号和干扰的垂直相关性是衡量阵列增益的一个重要指标,相关性由任意两个阵元输出之间的互相关系数来衡量。假设p1、p2是两个阵元产生的输出信号,互相关系数定义为:
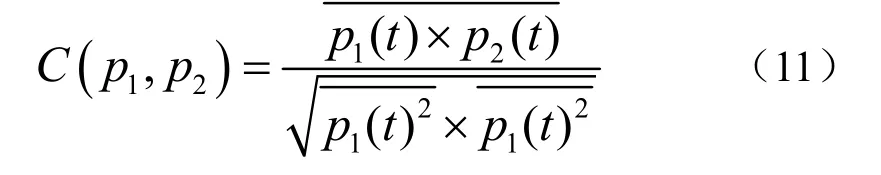
其中,上横线表示时间平均,分母是归一化因子。
考虑一个 33阵元的垂直接收线阵,阵元间隔2.5 m(半波长),阵中心与声源同深,目标深度为50 m。环境参数及发射信号与3.1节相同,图9为第 17号阵元与其它阵元的目标回波和混响序列的相关系数。可以看出,在Pekeris波导中,目标与接收相同深度条件下存在下述结论:(1)目标回波的相关半径大于混响相关半径,但两者的相关半径都较小。(2)相关半径内,目标回波的相关系数大于混响相关系数。
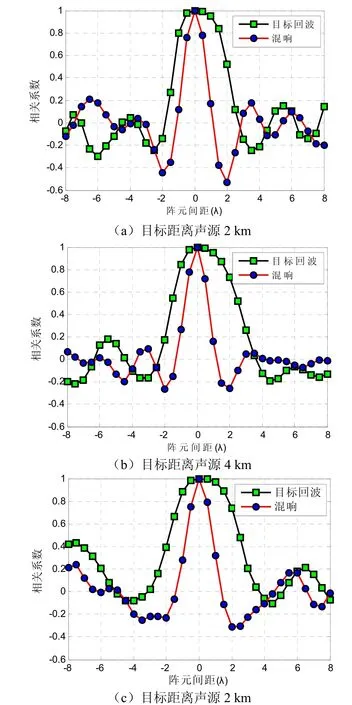
图9 混响和目标回波的垂直相关性比较
3.4 垂直线阵波束形成抑制混响
由于海底和目标散射特性的差异,混响中的高号简正波所占比重相对于目标回波更大,也就是高号简正波信混比较低。垂直线阵就是利用空间滤波特性,抑制略射角较大的高号简正波从而达到提高信混比的目的。下面利用仿真信号对常规波束形成抑制混响的效果进行分析,根据前文相关性分析结果选取33阵元中13-21号阵元信号作波束形成。
图10为垂直线阵接收混响和目标回波融合仿真信号的强度曲线,目标、环境参数及发射信号与前文相同。可以看出,波束形成后目标回波信混比明显提高,说明垂直线阵波束形成有一定抗混响的效果,当然在工程实践中阵形和环境因素会影响抑制效果。
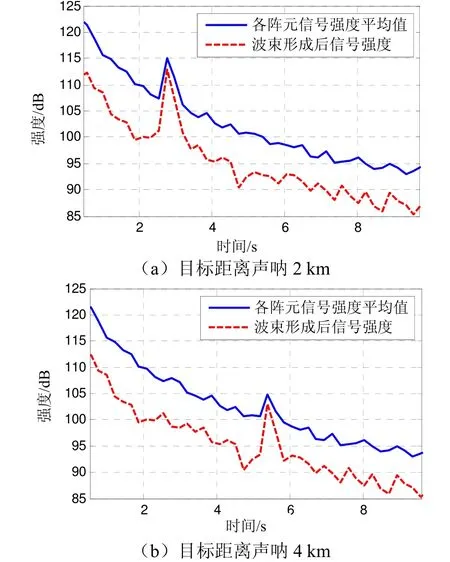
图10 仿真信号强度曲线
4 结论
借助简正波理论,给出统一形式的海底微元和目标散射场,结合源信号频谱给出了海底混响和目标回波融合仿真方法,仿真信号统计特征验证了该方法的有效性。通过对浅海刚性球目标进行实例仿真,表明目标回波的垂直相关性优于混响,垂直线阵波束形成能够在一定程度上抑制混响,可以为抗混响研究提供技术参考。
本文提出的融合仿真方法忽略了多次散射的影响,适用于浅海信道中远程目标的回波波形,不适用目标太靠近海底的情况;同时,由于简正波理论自身的特点,该方法适用于浅海中低频混响和目标回波融合仿真。对于高频或近场的情形,可以考虑采用射线方法代替简正波。

