一种k/n卷积码参数盲估计的鲁棒性方法
张云冲,戴旭初
(中国科学技术大学 信息科学技术学院,安徽 合肥 230026)
0 引 言
信道编码盲辨识技术指在通信链路中接收端在未知信道编码的情况下,仅根据接收序列,利用编码的冗余性对信道编码进行识别和分析,从而识别出其所使用的信道编码方式和参数. 卷积码是目前使用最为广泛的几种信道编码之一,针对卷积码盲辨识技术的研究较多[1,2]. 如图 1 所示,目前关于卷积码的盲辨识研究基本上都将识别过程分为三个步骤,即参数估计、监督矩阵识别和生成矩阵识别,并按照顺序逐一完成. 由于卷积码的生成矩阵和监督矩阵互为对偶矩阵,因此,研究重点集中在参数估计和监督矩阵识别上[3-6].
目前,k/n卷积码的盲辨识算法中,抗噪性能较好的算法一般使用GJETP算法进行参数估计,再通过求解对偶码的方式识别监督矩阵,并通过迭代算法提升算法性能[6]. 近年来,在已知编码参数的条件下对监督矩阵进行识别,可以达到非常好的抗噪性能,如文献[7]提出的基于Walsh-Hadamard变换的k/n卷积码监督矩阵识别方法. 但是在卷积码的参数估计方面,由于GJETP算法依赖于高斯消元法,因此对信噪比要求比较高,且GJETP算法每次迭代仅仅使用一个方阵进行高斯消元,其对接收数据的利用并不充分,导致卷积码参数估计的抗噪能力较差,从而限制了卷积码盲辨识的整体性能.
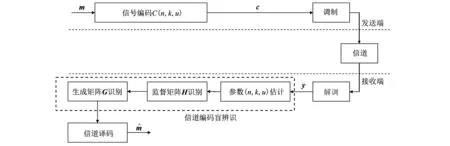
图 1 通信链路基本结构图Fig.1 A schematic diagram for a general communication link
本文提出一种基于Walsh变换的k/n卷积码参数的盲估计方法,能够充分利用接收到的数据. 假设系统使用卷积码进行信道编码,并且接收端已经获得经过解调和硬判决后完整的含错接收序列y. 信道码参数盲估计的主要任务是,仅根据接收序列y,对卷积码的编码参数(n,k,u)进行估计,这里n表示卷积码的码字长度,k表示信息位长度,u表示该卷积码的总体约束长度.
本文假定所识别的卷积码编码器是一个最优编码器,即在同样编码参数条件下具有最大自由距离的编码器[8]. 最优卷积码编码器在同样参数下具有更好的抗噪性能,并具有一些好的代数性质[9],充分应用这些性质将有助于卷积码参数的估计. 此外,本文假设通信系统在接收端使用硬判决,因此,可以将信道模型建模为二进制对称信道,用以等效高斯信道和硬判决两个处理过程.
1 卷积码与Walsh-Hadamard变换
1.1 卷积码的基本概念和性质
令C(n,k,u)表示一个具有k个输入,n个输出的卷积码,其中u表示该卷积码的总体约束长度. 可以使用一个k×n的多项式矩阵G(D)来表示卷积码C的生成矩阵,即
(1)
式中:gi,j(D)∈F2[D], ∀i=1,…,k, ∀j=1,…,n,是生成多项式;D代表延时操作符;F2[D]表示二元域上多项式环.
与文献[6]相同,本文令ui表示生成矩阵G(D)第i行的记忆深度,则卷积码的总体约束长度u可以表示为
(2)
如果记卷积码C的对偶码的生成矩阵为H(D),则H(D)为G(D)的一个监督矩阵,且文献[8]证明了在最优编码器条件下,监督矩阵的总体约束长度u⊥=u.
1.2 Walsh-Hadamard变换
Walsh-Hadamard变换(以下简称Walsh变换)是一种广义的傅里叶变换,目前在视频编码、快速频谱分析中都有广泛的应用[10]. 本文使用递归的方式定义k阶Walsh-Hadamard矩阵,即
(3)
Walsh变换定义W为整数域向量到自身的一个映射,即W∶Zn→Zn,记整数域上的向量v=[v0,v1,…,v2N-1],则可以将Walsh变换表示为
W(v)=vH(N)=V=[V0,V1,…,V2N-1],
(4)
称V是v的Walsh谱. 令
(5)
称Vmax为v的Walsh谱峰值.
文献[11]给出了关于Walsh-Hadamard矩阵的另一个重要性质,其第i行第j列的元素Hij可以表示为
(6)
式中:in和jn代表i和j对应的二进制向量,且i,j= 0.1,…,2N-1.
1.3 利用Walsh变换求解二元域上线性方程组
在数字序列分析中,经常会遇到求解二元域上线性方程组AxT=0问题,这里A是定义在二元域上的mn维矩阵,x是定义在二元域上待求解的1n维行向量,T代表转置. 根据文献[11],可以利用Walsh变换求解该二元域的线性方程组,具体的方法为:
1) 根据所需的置信度或者虚警概率选择合适的判决门限γ;
2) 统计A的行向量出现频次,构造一个用以Walsh变换的行向量v;
3) 对v应用Walsh变换得到其Walsh谱V;
4)V中大于门限γ的分量下标对应的二进制向量即为AxT=0的解集.
2 卷积码参数的盲估计
卷积码参数盲估计的目的是仅根据接收序列y,估计出卷积码的参数.
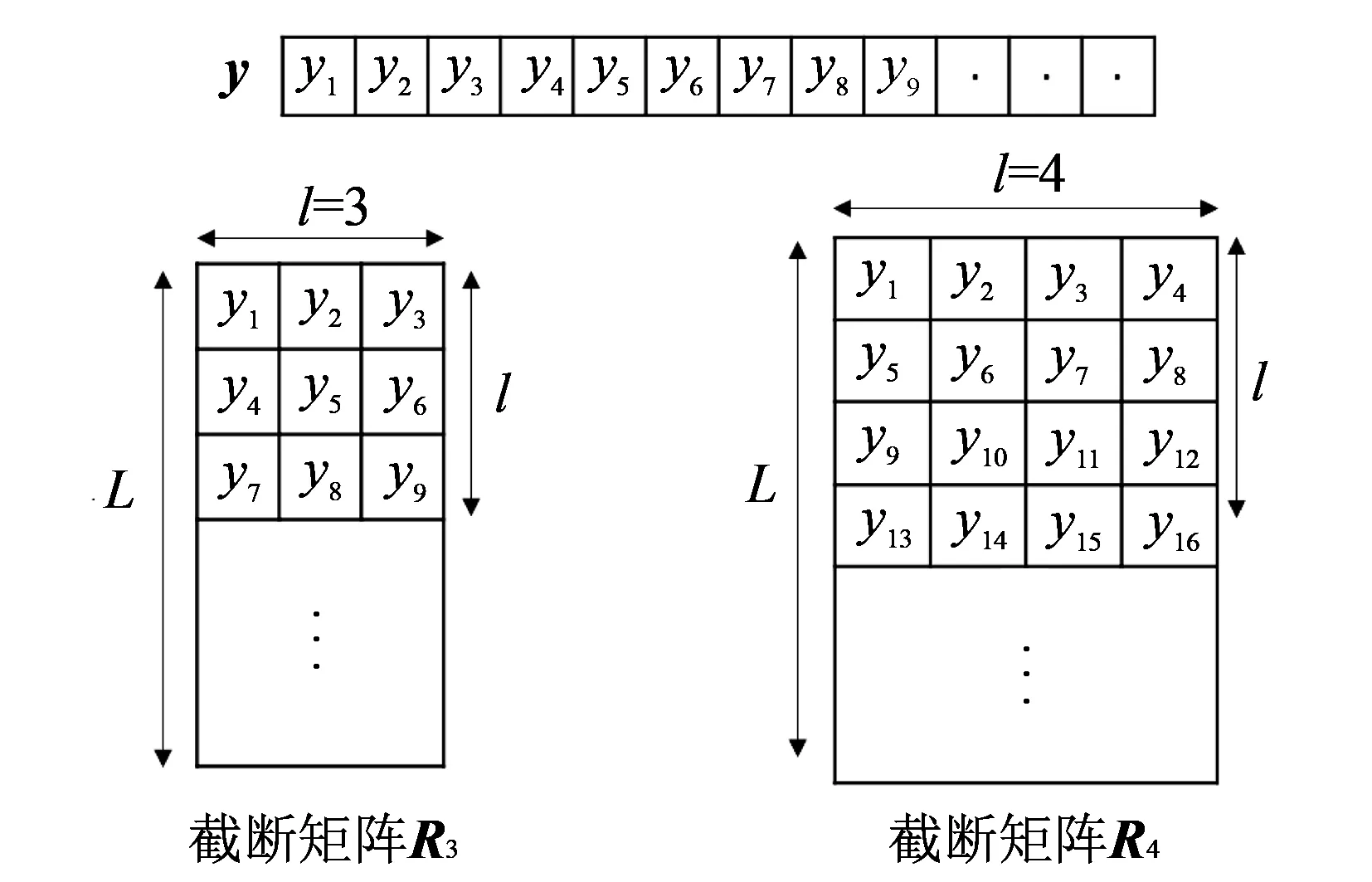
图 2 构造截断矩阵Ri的示例图Fig.2 Examples of constructing truncation matrix Ri
2.1 基本原理
首先,利用接收序列y构造截断矩阵. 接收序列y是一个比特流序列,即y=[y1,y2,…]. 依次使用序列y的元素从左至右、从上至下构造一个Ll的矩阵Ri,l表示截断矩阵的列数,并称Ri为接收序列y的截断矩阵,图 2 给出了截断矩阵的两个例子.
其次,考察截断矩阵Ri的秩亏特性. 假设传输信道无噪声,即接收序列y不含错,根据文献[6],由k/n卷积码编码的接收序列y构成的截断矩阵Ri在二元域下具有如式(7)的秩特性
(7)
式中:α是正整数;nc是当l从小到大递增时,第一次使得截断矩阵Rl秩亏的l,且

(8)
根据上述性质可知,随着l的增加,截断矩阵Ri会有周期性的秩亏,其周期就是码字长度n. 基于秩亏的周期性以及式(7)和式(8)的关系,可以将需要估计的三个参数(n,k,u)联系起来. 因此,分析截断矩阵Ri的秩亏特性,可以实现卷积码参数的估计.
2.2 鲁棒性估计方法
对于有噪信道,由于噪声的干扰,式(7)将不再成立. 考虑到含噪的截断矩阵Ri是否秩亏等价于含错方程是否有非平凡解,从而可以根据1.3中给出的方法来求解这个二元域上线性方程组.
选取合适的截断矩阵最大列数lmax,分别对l=1,2,…,lmax的截断矩阵Ri应用Walsh变换,得到其Walsh谱Vi,用z(l)表示Vi中大于门限值的分量数量,即
Z(l)=card{Vli>γ|i=1,2,…,2′-1},
(9)
则两个非零z(l)之间的间隔就是要估计的参数n,且可以使用
rank(Ri)=l-[log2(Z(k)+1)]
(10)
来估计Rl的秩.
假设找到相邻的两个秩亏的截断矩阵Rl1和Rl2,并得到其秩rank(Rl1)和rank(Rl2),则有
(11)
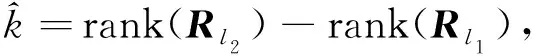
(12)
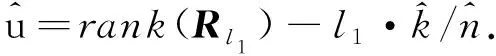
(13)
为了进一步增加参数估计的鲁棒性,可加入相邻谱峰值差距不能过大这一约束条件. 若用d表示相邻谱峰值的比值,则一般可取d∈[0.7,1.5].
基于上述分析,一个完整的卷积码参数的鲁棒性估计算法描述为:
输入: 接收序列y,判决门限γ,截断矩阵的行数L
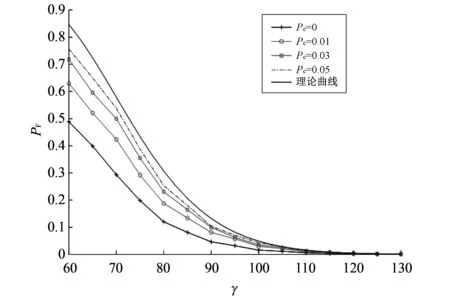
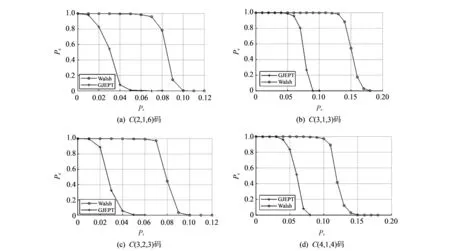
初始化:l=1,f=0,h=0,d1,d2whilel 使用接收序列y构造L×l的截断矩阵Ri 对Ri应用Walsh变换得到谱向量Vl,以及Vl的谱峰值mi Z(l)=card{Vli>γ|i=1,2,…,2l-1} ifml>max(γ,d1*h) then iff=0‖f=l-1‖ml>d2*hthen f=l h=ml else 返回参数,算法结束 end end l=l+1 End 在参数估计算法中,d1和d2是用以控制判断秩亏的谱峰值差距的经验参数,一般取d1=0.7,d2=1.5即可;f是前一个谱峰对应的截断矩阵宽度,h是前一个谱峰的谱峰值. 最后,简要分析一下卷积码参数盲估计的计算复杂度. 可以看出参数识别方法的主要计算量在于Walsh变换. 对于长度为l的实序列,快速Walsh变换的复杂度为O(l·2l),因此,本文方法的计算复杂度为O(lmax·2lmax). 在卷积码参数估计算法中使用了一个检测门限,用来挑选Walsh谱中的谱峰. 如果选取过大,会导致在信道传输错误率较高的情况下丢掉真实谱峰,即漏警; 如果选取过小,又会导致一些虚假谱峰的出现,也就是所谓的虚警. 本小节将分析研究门限γ与虚警概率P之间的关系,在达到预期虚警概率P的同时,最小化γ,使得漏警概率最低,从而提升参数估计算法的性能. 对截断矩阵Rl应用Walsh变换,可以看作将Rl中的行映射到Walsh-Hadamard矩阵中的行,再将被映射的行在整域中相加,得到的行向量就是Walsh变换后的结果. 因此,截断矩阵Rl的Walsh谱第i个分量i=1,2,…,2l-1,也是截断矩阵Rl中的行,与Walsh-Hadamard矩阵中的元素相对应,每一行映射成1或-1. 由于Rl的行具有随机性,其映射结果可以看作一个取值为{1,-1}且满足等概分布的离散随机变量,记为ξi,j,j=1,2,…,L. 则对于Rl的Walsh谱的第i个分量,令 如果i对应的二进制向量并不是线性方程组的一个解,但有ξi>γ,则产生一次虚警. 记ξi的概率密度函数为FL(x),由于ξi,j,j=1,2,…,L,满足独立同分布,可以根据De Moivre-Laplace定理得到 (14) 式中:E{ξij}和Var{ξi,j}分别表示ξi,j的均值和方差;P{·}是概率函数. 由于E{ξi,j}=0以及Var{ξi,j}=1,所以,Φ(x)是正态分布的累计分布函数. 记单个谱峰分量产生虚警的概率为Pfa,当L较大时,由式(14) 可以得到 (15) 对于长度为2l的Walsh谱,当各分量相互独立时,其整体的虚警概率PF为 PF=1-(1-Pfa)2l. (16) 如果要求参数估计算法的整体虚警概率不大于P,即PF≤P,则根据式(15)和(16)可以得到 (17) 式中:Φ-1(·)表示Φ(·)的反函数. 在保证整体虚警概率小于等于P同时,应使漏警概率最小,即γ应取较小的值. 因此,式(17)取等号即可得到最优门限γopt,为 (18) 图 3 C(3,1,3)码的门限值γ与虚警概率PF关系Fig.3 The relationship between threshold γ and false alarm probability PF of C(3,1,3) 主要考察在不同的检测门限γ下,通过实验统计得到的虚警概率,以及与基于理论分析得到的虚警概率之间的关系. 仿真条件设置为: 采用C(3,1,3)码编码器对数据信息进行编码,数据矩阵Rl的行数L=1 000,统计结果是通过10 000次蒙特卡洛仿真实验结果的平均值. 图 3 给出了在信道传输错误率Pe=0,0.01,0.03,0.05四种情况下,参数估计算法门限γ与虚警概率PF的关系曲线,图中理论曲线由式(15)和式(16)计算得到,其余曲线都是通过实验统计获得的. 从图 3 可以看到,理论曲线是真实虚警概率的上界,并且随着Pe的增大,实验结果逐渐接近于理论曲线. 这是因为式(16)是在Walsh谱分量之间相互独立这一假设下导出的,但在无噪或低噪声情况下,这一条件并不严格成立,各个谱分量之间有一定的相关性. 但是随着噪声增大,从Rl到Walsh谱之间的映射趋向随机,导致各个谱分量之间的相关性减弱,从而使得实际关系曲线逼近理论曲线. 另外,通过图 3 还可以观察到,在给定虚警概率的约束下,由式(18)确定的谱峰检测门限γopt要高于实际需要的门限,这将导致漏警概率有所增加. 但是在实际应用中,由于缺乏信道传输错误率、编码器参数等先验信息,利用式(18)来确定检测门限仍是一个较好的选择. 针对四个不同的卷积编码器,考察本文提出的参数估计方法的性能与信道传输错误率的关系,并与文献[6]中GJETP算法的性能进行对比. 仿真条件设置为: 信息序列为3×104Bit,截断矩阵Rl最大列宽lmax=30,行数L=1 000,四个卷积编码器分别是C(2,1,6),C(3,1,3),C(3,2,3)和C(4,1,4). 用参数估计的正确率Pc作为评价参数估计方法性能优劣的指标,其定义为 Pc=参数估计正确的次数/蒙特卡洛仿真实验的总次数. 仿真实验中,蒙特卡洛仿真实验次数设为1 000. 图 4 给出了本文提出的算法(Walsh)、GJETP算法的参数估计正确率Pc与信道传输错误率Pe的关系曲线,其中图 4(a)~(d) 分别对应四种不同编码器. 图 4 四个卷积码的参数估计正确率Pc与信道传输错误率Pe关系Fig.4 The relationship between probability of correct parameters estimation Pc and channel error probability Pe of four convolutional encoders 从图 4 可以看出,本文提出算法的性能对不同编码器均优于GJETP算法; 在Pc相同的条件下,本文方法所对应的Pe要高于GJETP算法,这表明本文方法的抗噪性能要优于GJETP算法. 另一方面,在Pe≤0.07时,本文方法对不同编码器的识别正确率均达到了95%以上. 本文提出了一种基于Walsh变换的卷积码参数盲估计方法,可以从含有较大噪声的接收序列中完成k/n卷积码编码参数(n,k,u)的估计. 相较于现有的算法,本文提出的方法具有更好的抗噪性能,在信道传输错误率Pe≤0.07时,本文方法对不同编码器的识别正确率均达到了95%以上,具有良好的实用价值. 在很多使用卷积码编码的通信系统中可能对卷积码加入删余结构,因此,如何识别其母码和删余结构是未来工作的一个方向; 另一方面,现有通信系统接收机很多采用软判决而不是硬判决方式进行译码,因此,改进算法使之适用于软判决译码的通信系统是一个值得深入研究的一个课题.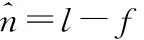
2.3 门限的选择
3 仿真实验结果与分析
3.1 检测门限γ与虚警概率PF的关系
3.2 卷积码参数盲估计算法的性能与信道传输错误率的关系
4 结 论

