大跨连续刚构桥零号块力学性能分析

许基厚， 王　成， 唐自航， 何南润

(1.西南交通大学土木工程学院，四川成都 610031；2.中国五冶集团有限公司，四川成都 610063)

零号块是刚构桥的关键部位， 其构造复杂，且存在纵向、横向及竖向预应力的作用，使得其成为全桥应力分布较为复杂及易开裂的部位，而且主桥结构施工过程中存在着体系转换，结构局部变形受力更加复杂，故有必要对零号块进行详细的应力计算分析，确保零号块的受力合理[1-5]。本文将结合一座主跨为210 m的大跨连续刚构桥的零号块进行有限元建模，分析零号块的受力特点。

1　工程概况与有限元模型

1.1　工程概况

本桥采用(5×40+110+210+110+5×40) m跨径，主桥箱梁零号块的立面图和断面图如图1所示，零号块混凝土采用C60；零号块纵向预应力钢筋采用22Φs15.2，张拉控制应力为1 395 MPa；体外预应力采用19Φs15.2和27Φs15.2两种规格，张拉控制应力为1 116 MPa，因体外预应力是在运营期出现超期的挠度或者改善受力而进行后加的预应力，因此在成桥时不考虑体外预应力，计算零号块局部受力分析时未考虑体外预应力；零号块顶板横向预应力采用3Φs15.2规格，零号块隔板采用7Φs15.2规格，张拉控制应力为1 395 MPa；零号块竖向预应力采用3Φs15.2规格，张拉控制应力为1 302 MPa。

1.2　有限元模型

由弹性力学中的圣维南原理[6-7]可知，零号块的应力分布只与其附近区域的应力状态有关，而远离零号块的区域中的应力状态，对零号块的应力分布影响是很小的，一般可以忽略不计。所以，只需取出零号块，并考虑零号块附近区域的作用，进行空间应力分析。

在对零号块分析时先用桥梁博士软件对桥梁作整体计算，即计算出2号块结合面处各种工况荷载组合作用下的弯矩、轴力和剪力，将其转换为相应的边界力，再将其转化为ANSYS分析模型相应截面上的分布面力和节点集中力，然后再按空间有限元法分析零号块的应力状况。零号块边界力的施加通过2号块进行传递，2号块端部截面形心作为主节点，面内其它节点为从节点，将两者的自由度进行耦合，以方便边界集中力的施加。混凝土实体部分有限元模型如图2所示，纵向、横向及竖向预应力筋部分有限元模型如图3所示，墩底约束和边界约束如图4所示。本文主要关注零号块和横隔板的受力情况，箱梁的三向预应力钢筋作用采用整体施加的方式，以LINK8单元模拟预应力钢筋并通过施加初应变的方法实现其作用。本文模型的建立主要分为以下几个部分：

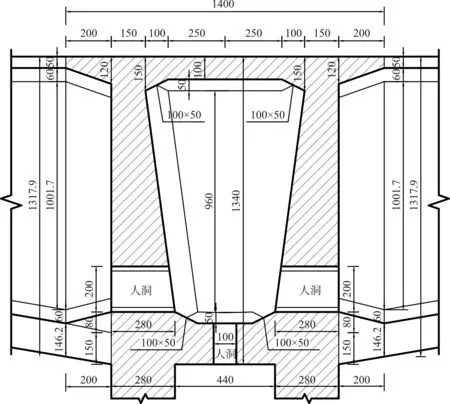
(a)立面图

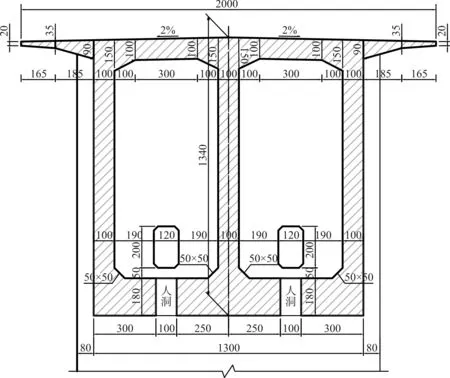
(b) 断面图图1　零号块立面与断面(单位:cm)

(1)零号块主要采用从下向上的方法，分别建立实体大的箱梁模型和箱梁的芯模再对其进行布尔运算形成。

(2)桥墩通过对零号块底面的相对应的面拉伸来形成墩身实体模型。

(3)预应力与混凝土节点耦合。

图2　混凝土实体部分有限元模型

图3　纵向、横向及竖向预应力筋部分有限元模型图

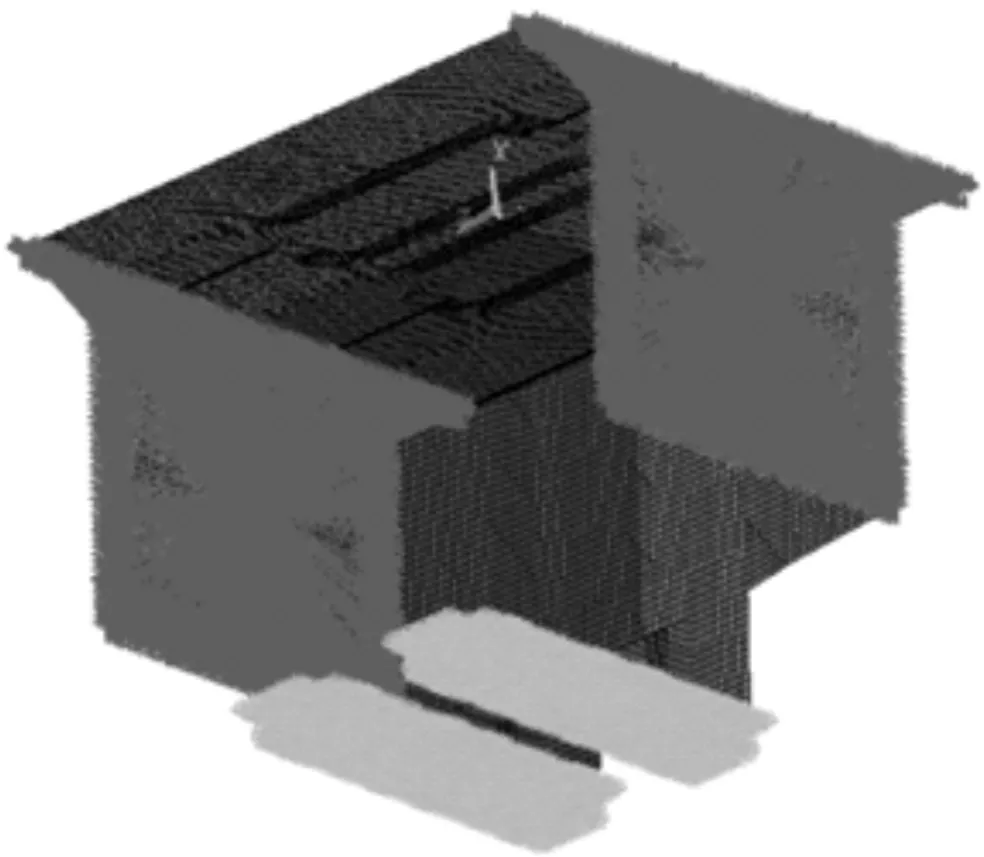
图4　有限元边界处理模型

2　有限元分析方法

利用有限元弹塑性理论[8-10]的几何方程、本构方程、虚功原理或位能变分方程求解单元节点力与节点位移关系的表达式，即单元刚度矩阵。根据几何方程可以建立单元内的应变矩阵表达式如式(1)所示。

{ε}=[B]{δ}e

(1)

对于小变形线弹性问题，根据物理方程建立单元内的应力矩阵如式(2)所示。

{σ}=[D]{ε}=[D][B]{δ}e

(2)

根据虚功原理可以求出单元中的节点力如式(3)所示。

{F}e=[k]{δ}e

(3)

对于结构是任意一点建立平衡方程可以得到结构整体有限元平衡方程如式(4)所示。

[K]{δ}={R}

(4)

式中：[B]为几何矩阵，[D]为弹性矩阵，[k]为单元的劲度矩阵，[K]为整体劲度矩阵，[δ]为整体节点位移矩阵，[R]为整体节点荷载矩阵。

3　计算分析及结果

3.1　工况与荷载施加

本文是研究零号块承载能力极限状态基本组合、正常使用极限状态基本组合和标准组合三种情况下的的局部受力分析。二号块端部力由全桥整体计算而得到，并且以节点集中力的形式施加到局部分析模型二号块端部。工况1为承载能力极限状态基本组合，工况2为正常使用极限状态基本组合，工况3为正常使用极限状态标准组合。表1为桥梁博士提取三种工况下的边界内力。

3.2　分析结果

因工况2的结果整体小于工况3的结果，所以只对工况1与工况3进行分析。

因为篇幅有限，只列出了工况1最大轴力下的应力分布云图(图5～图8)。由图5可以看出零号块的最大横向拉应力约为2.5 MPa，出现在横隔板上部和顶板预应力筋锚固位置，满足混凝土的抗拉强度标准值2.85 MPa。最大横向压应力约为15 MPa，主要是由于横向预应力作用引起，出现在底板横向预应力作用区域。由图6可以看出零号块的最大竖向拉应力约为2.6 MPa，出现在横隔板与腹板交界位置处，满足混凝土的抗拉强度标准值2.85 MPa。最大竖向压应力约为32 MPa，主要出现在横隔板底部与腹板连接的区域。由图7可以看出零号块最大纵向拉应力分布在整块横隔板上，其值大约1.3 MPa，最大纵向压应力主要分布在整个顶板区域，其值大约28 MPa，忽略预应力钢束端部的局部集中应力。由图8可以看出零号块等效应力的较大值分布于顶板位置，与预应力筋锚固的交界处的等效应力最大，最大值约为36 MPa，符合C60混凝土强度的要求。

图5　零号块X向应力分布

由表2可以看出，承载能力极限状态下与正常使用状态下的应力分布规律明显不同，承载能力极限状态下在正负弯矩最大的情况下，截面受力相对不利，拉压应力都接近规范规定的限值；在剪力最大的情况下，只有正截面的压应力达到了35 MPa，但依然满足规范要求。正常使用极限状态下应力整体上比承载力极限状态下的小，特别是在最大轴力与最大负弯矩情况下，结构的空间应力安全储备较大；结构的最大压应力为30 MPa，发生在竖桥向的最大正弯矩下，最大拉应力为2.5 MPa，发生在竖桥向的最小轴力与最小剪力下。

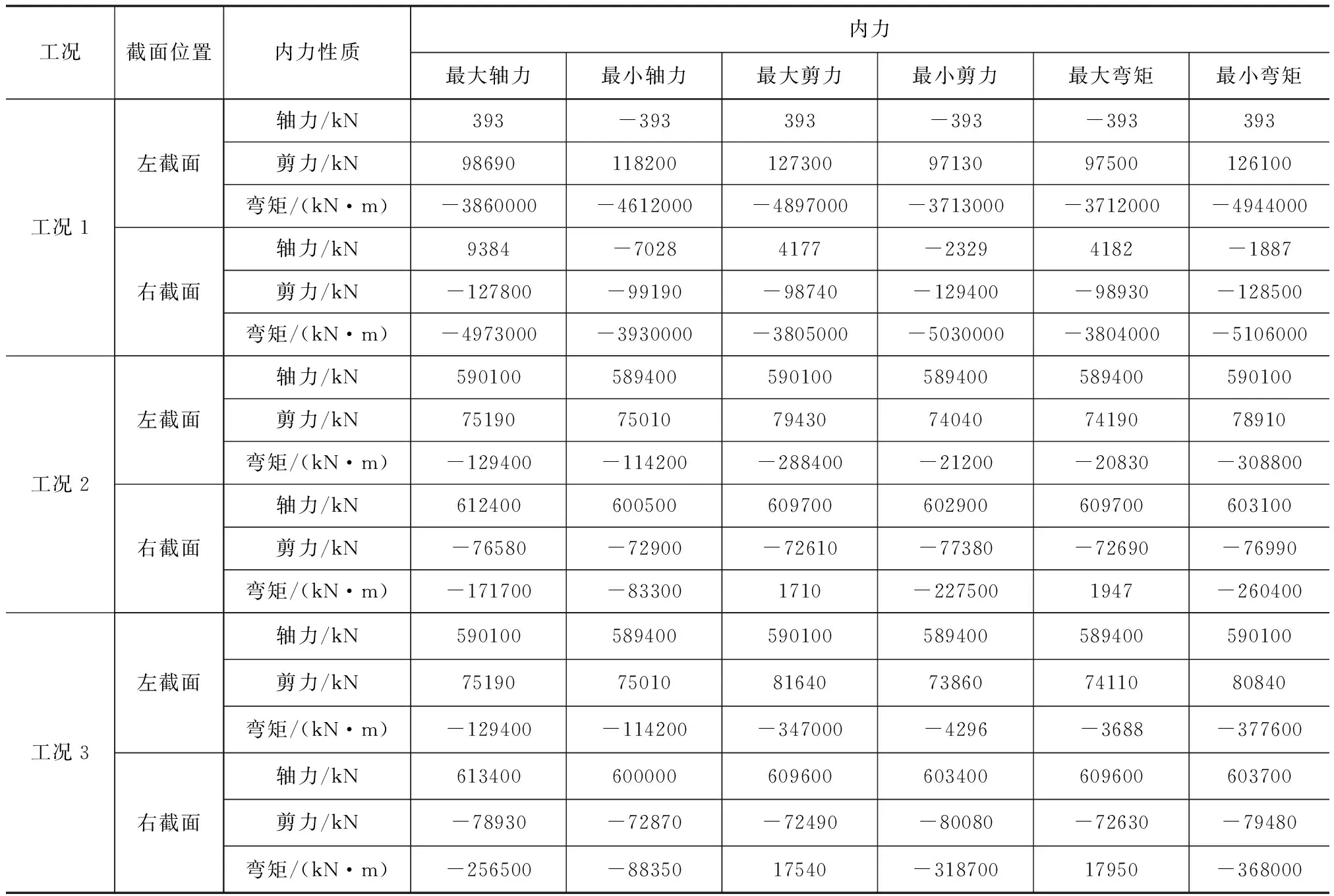
表1　桥梁博士提取三种工况下的内力

图6　零号块Y向应力分布

图7　零号块Z向应力分布图

图8　零号块VonMises应力分布

表2　零号块应力计算结果

4　结论和建议

针对该主跨为210 m的大跨连续刚构桥的零号块，进行短暂工况承载能力极限状态和正常使用极限状态的应力分析，考虑零号块中各种最不利内力组合，得出以下结论：

(1)零号块的主要受拉区域为横隔板、横隔板与腹板和顶板的交界位置处以及顶板预应力钢筋的锚固位置，但根据计算其拉应力均小于规范容许值。

(2)零号块的顶板、腹板、底板主要表现为受压，其中较大压应力分布在顶板和腹板上半部分，顶板处于三向压应力状态，最大压应力值也满足规范要求。

(3)由于本模型没考虑普通钢筋的作用，实际结构中配有较多普通钢筋，有较好的应力传递作用，以及防止局部受拉开裂，这对结构应力分布是有利的。