粘弹性边界条件的实现及在地震动场地效应研究中的应用

黄　云，奉建军

(西南交通大学土木工程学院，四川成都 610031)

在地震波场数值模拟研究中，通过建立有限尺寸的模型来模拟半无限空间，这时通常需要在模型的边界引入虚拟的边界来吸收边界上的波动能量，从而消除边界反射。

在一维波动理论的基础之上，Lysmer和Kuhlemeyer[1]提出了粘性边界条件，该理论采用了粘性阻尼器来模拟无穷远边界。其物理意义明确，处理方法简单，但存在低频失稳、精度不够和不能模拟地基弹性恢复的特点。在柱面波动的理论基础之上，Deek[2]提出了二维时域人工边界条件。在Deek的基础之上，刘晶波等[3]提出了二维时域粘弹性边界条件，并且在球面波的理论基础上又推导了三维时域粘弹性边界。

1　粘弹性边界条件

依据刘晶波等[3]提出的粘弹性边界条件，其等效物理系统的弹簧的刚度系数与阻尼器的阻尼系数分别为：

切向边界：

(1)

法向边界：

(2)

式中：KBT与KBN分别为弹簧的切向刚度与法向刚度；CBT与CBN分别为切向阻尼系数与法向阻尼系数；R为波源至人工边界点的距离；Cs和Cp和分别为S波和P波波速；G为介质的剪切模量；ρ为介质质量密度；αN和αT分别表示粘弹性边界条件的法向参数与切向参数。在二维研究中αT取值的区间建议在[0.35，0.65]，αN取值的区间建议在[0.8，1.2]。本文取值为αT=0.5,αN=1。

2　粘弹性边界条件在ABAQUS中的实现

在ABAQUS有限元分析软件中，在软件中Interaction模块下，通过在模型的边界上布置弹簧与阻尼器来模拟粘弹性边界，弹簧的刚度系数K与阻尼器的阻尼系数C分别可由式(1)与式(2)得到。该方法的理论依据是通过在模型边界上布置弹簧与阻尼器分别来提供弹性恢复力与吸收入射波动能量。

为了验证在ABAQUS中粘弹性边界条件的实现效果，建立如图1所示的二维模型。模型的尺寸大小为200 m×100 m，有限单元的网格大小为0.5 m，在模型上边中部位置施加荷载，观测点于震源点两边对称布置，每个观测点间距为3 m，共48个；施加的荷载为方向竖直向下频率为10 Hz的正弦波y=sin0.2πt，得到如图2所示的记录。图2(a)为在不施加任何边界条件采用默认值的情况下所测得的地震时间记录，图2(b)为施加粘弹性边界后所测得的地震时间记录。

图1　模型示意

(a)默认边界地震记录 (b)粘弹性边界地震记录图2　时间记录

图2(a)表明在默认的边界下，观测排列接收到了底边界与侧面边界的反射波，由于这些边界反射波存在使得地震资料处理起来较为困难。图2(b)表明在模型左右边界及底边界施加粘弹性人工边界后，观测排列只接收到来自于震源的直达P波与直达S波，此证明了粘弹性边界的有效性，其能够有效的吸收反射波动能量。

图2(b)为Dirichlet边界和粘弹性边界下模型的波场快照，通过对比可以看出Dirichlet边界下各种边界反射波叠加在一起，波场变得非常复杂，使波的辨别难度增加。

3　粘弹性边界上地震波震源加载方法

实际问题中的地震波的加载应当是外源波动的加载，震源实质是处于人工边界无限远的地方。对于粘弹性边界之外的无穷区域，能够将该区域中的总波场分离为散射波场和自由波场。在人工边界计算区域之内，散射波场反射的波动能量由在粘弹性人工边界处布置的弹簧-阻尼系统吸收，而由自由波场产生的波动能量可以转化为粘弹性人工边界处的应力边界条件。在该理论的基础之上，刘晶波和吕彦东[4]提出将地震波震源的加载问题转化成波源问题，把加载的地震波震源转变程施加在粘弹性边界上的等效荷载。

假定加载的波场为u0(x,y,t)，粘弹性边界上的位移为u0(xB,yB,t)，若在粘弹性边界上施加的等效荷载使得粘弹性边界上的位移和应力与原自由场相同,则表明实现了地震波震源的准确加载，即：

u(xB,yB,t)=u0(xB,yB,t)

(3)

τ(xB,yB,t)=τ0(xB,yB,t)

(4)

式中：τ0为原连续介质中由位移U0产生的应力。

假定在粘弹性边界上某个节点加载的等效应力是FB(t)，按力学中脱离体的概念，把弹簧和阻尼器组成的物理系统与之脱离，此时粘弹性边界上该点的应力应为：

τ(xB,yB,t)=FB(t)-fB(t)

(5)

式中：fB(t)为弹簧与阻尼器跟边界上节点连接的内力。将式(4)代入式(5)得：

FB(t)=τ0(xB,yB,t)+fB(t)

(6)

由弹簧-阻尼器的运动方程：

(7)

将式(3)代入式(6)得到人工边界上施加的等效荷载应为：

(8)

由此即可完成在粘弹性边界上加载地震波震源。

从式(8)可看出在粘弹性边界节点上的等效荷载由自由场地震波动产生的应力、克服由弹簧产生的抗力与克服由阻尼器产生的抗力三者构成。

4　粘弹性边界在地震动场地效应二维数值模拟中的应用

地震动的场地效应问题一直是工程地震学的研究重点，大量的研究表明场地土本身对地震波的传播有较大影响，不同的场地条件下地震动引发地面上的震害效果差异显著[6-8]。坚硬场地土上的土木工程结构的破坏通常是由地震作用所引发，而在软弱场地土上时，往往是由于地基土液化、不均匀沉降等因素引发地基土失稳，从而导致结构破坏。总体来说，当场地上的覆盖土层越为松软、覆盖层的厚度越厚时，处于该场地上的土木结构所受震害情况越发严重。

为表示场地覆盖土层变化对地震动的反应影响情况，定义地震动放大系数β：

β=Umax/Us

(9)

式中Umax为覆盖层地表观测点峰值位移，Us为场地无覆盖层时均匀场地观测点峰值位移。

为了研究地震动的场地效应的变化规律，使用数值模拟软件ABAQUS建立如图3所示的两组二维场地模型，并应用粘弹性边界条件。在第一组模型中，模型底部基岩密度为2 000 kg/m3，泊松比0.25，S波波速为1 200 m/s，上部覆盖层密度为ρ=1 800 kg/m3，厚度h=60 m，泊松比υ=0.35，S波波速Vs依次为100 m/s、150 m/s、200 m/s、250 m/s、300 m/s、350 m/s、400 m/s、450 m/s，震源为基岩底部垂直入射正弦SH波sin2πt(0≤t≤1)。在第一组模型的基础之上仅把覆盖层厚度增加到h=90 m，由此成为第二组模型。通过对分析地表峰值位移放大系数β的变化情况来研究场地覆盖层软硬程度Vs及厚度h对震害的影响。

图4给出了覆盖层厚度h=60 m及h=90 m的条件下，放大系数β随覆盖层剪切波波速Vs变化的图像。从图中可以得出放大系数β随场地覆盖层剪切波波速Vs的变大而减小，但随着Vs的增大，这种变化情况呈减缓的趋势，说明当土体剪切波较小的时候(Vs<250 m/s)，场地对地震动的变化更为敏感。此外，场地覆盖土层剪切波速相同时，覆盖层厚度h较大的场地放大作用更为明显。

图3　成层场地示意

5　结论

本文在有限元模拟软件ABAQUS中利用阻尼元件和弹簧进行并完成了粘弹性人工边界的施加。此外，建立了二维模型进行全波场的数值模拟，数值结果显示该边界能够有效的实现对边界反射波动能量的吸收。基于此，将其应用到地震动场地效应研究中，模拟得到了场地覆盖土厚度及剪切波速对地震动场地效应的影响规律。

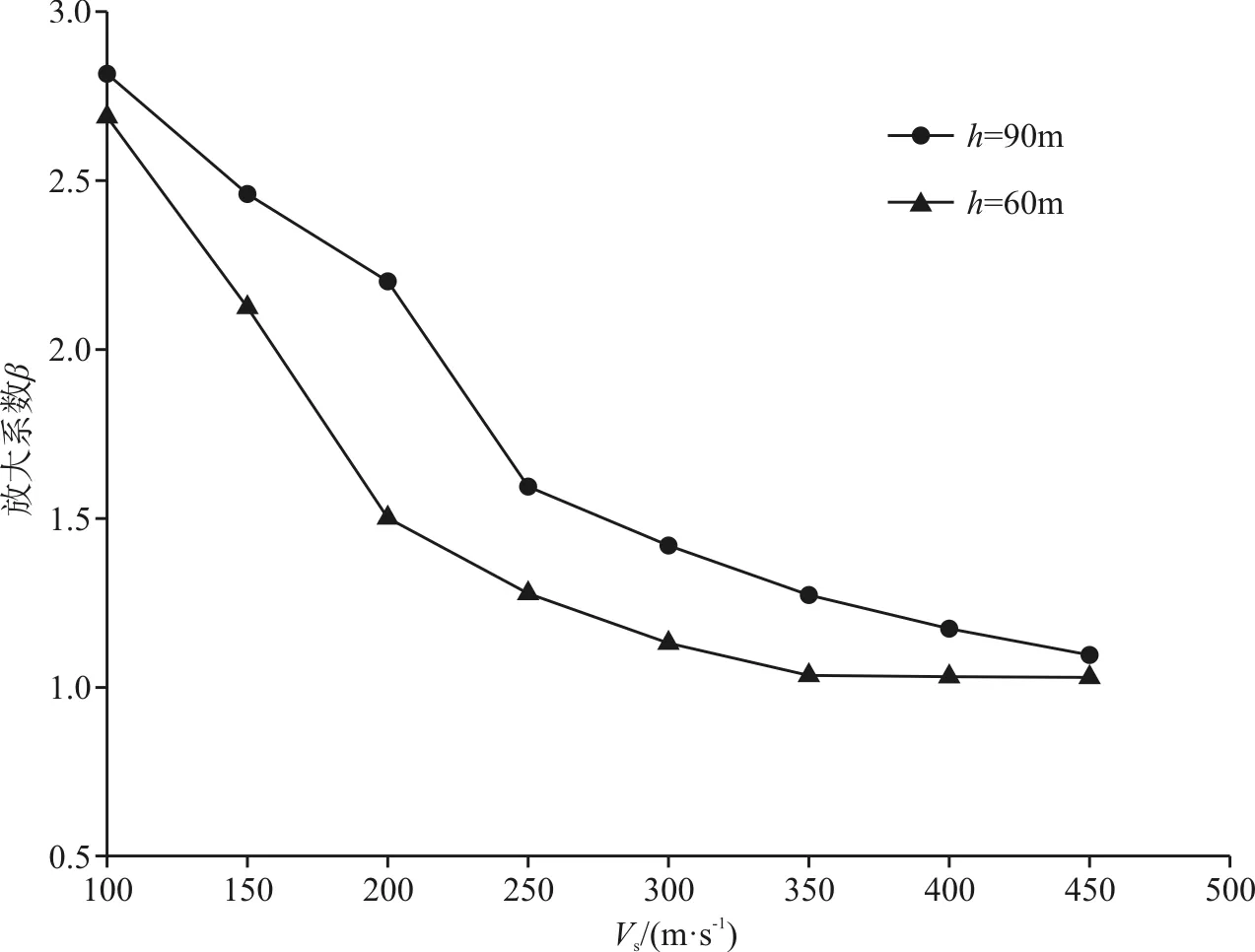
图4　β随场地覆盖土层厚度h及剪切波速Vs变化规律