基于混沌理论的X射线数字图像加密研究∗

张乃元 慕林洹 赵旭东 刘 宁

1 引言

管道是现行的五大运输工具之一，其在运送石油、天然气等方面具有独特的优势，管道运输是使世界石油工业得以规模化发展且已被实践证明为最有效的技术方法。我国石油的输油管线是国家能源的核心。石油管线传送油时需要承受几百个气压，微弱的焊接缺陷问题就会造成安全事故。所以，焊接检验水平的高低是焊接实施人员的难题与考验。使用X射线对产品的检测，是我们常常实行的方式，X射线的处理系统把已经产生的X射线图像输入到计算机，然后它能够转换为数字图像，与此同时也能够让物体内部的结构的详细信息展示出来，接着，再由相关技术人员分析与评判，从而达到焊缝的质量检测的要求。这是确保焊接的产品质量的关键的技术。接下来，对已经检测好的焊缝图像进行加密也是重要的一个环节，这样可以确保检测好的焊缝图像不被随意更改、破坏，同时也有助于后期环节的再操作。整个系统中，加密技术的好坏不仅能够使得前期工作得到保障，避免不必要的麻烦，也使得检测好的图像能更好地保存下来，因此，我的研究课题具有重要的意义。

2 混沌序列发生器模块

密钥流发生器决定着整个X射线图像加密系统的安全性［1］。若是密钥流发生器可以很好地生成完全无序的随机序列，则该加密系统加密后的X射线图像信息必定难以预测，也就说明了该系统的安全性很高。所以对于密钥发生器的选择尤为重要，必须确保发生器具有良好的随机性能。由于自然界中各种因素的影响，序列的完全随机是不可能存在的［2］。所以在选择设计必须确保发生器生成的伪随机序列要具有良好的随机性且周期性要足够长。混沌通常被定义为一种类似随机、貌似无规则的现象［3］。根据学者们的大量研究显示，存在大量的非线性系统，对其初始值进行微小的改变时，整个系统的状态和长周期性能都会因此而发生巨大变化，这就是通常所说的“蝴蝶效应”现象，即整个系统对其初始值有十分强的依赖敏感性［4］。误差在自然界中是不可避免的，在物理层面上来说，整个系统周期性的长期行为是完全随机的预测［5］。它是由于本身所特有的随机性而引起的，这种本身系统所特有的随机系数或是随机项而引起的随机现象有本质上的不同［6］。因此对于序列发生器的选择就应该是适合X射线图像特性的固定混沌算法，这样就会产生符合要求且令人满意的伪随机序列。

设计混沌序列发生模块的首要问题就是如何选取适合X射线图像的混沌映射来生成符合要求且令人满意的伪随机序列。由于Logistic映射被学者们研究的最为深入透彻，且其形式简单适合X射线图像特点，学者阐述了六种混沌映射其中包括Logistic映射在内，他们生成的二值混沌序列NIST所指定的随机序列测试标准进行测试比对，结果表明一维Logistic映射生成的混沌序列在其16项标准测试中通过了其中的15项测试标准，NIST（Nation Institute of Standards and Technology）即美国国家标准技术研究所［7］。因此在X射线图像加密系统中选择使用Logistic映射来生成混沌序列。

X射线图像加密系统选择的Logistic映射为xn+1=rxn(1-xn)。下面介绍它在X射线图像加密中的重要特性［8］。

其中当r=4时，Logistic映射产生混沌序列的概率分布函数为

分析概率分布函数可以计算出混沌序列的均值和相关函数，公式如下：

分析可知Logistic映射所产生混沌序列的联合概率分布函数 ρ(x,y)=ρ(x)·ρ(y)，自相关函数就等同于函数δ(1)。也就是说Logistic映射所产生混沌序列是其混沌特性等同于白噪声，分析可知在3.5669＜r≤4时，Logistic映射所生成的混沌序列是令人满意的伪随机混沌序列，综上所述，完全可以使用Logistic映射所生成的混沌序列用于X射线图像加密。分析可知当r值大于3.5669时，Logistic映射所生成的序列开始产生混沌，当3.5669＜r≤4时混沌序列的数值几乎完全能够在［0，1］间遍历，Logistic映射分岔图像如图1所示。

图1 Logistic映射分岔图像

基于Logistic映射生成的混沌序列的本身特性，本文对其进行了研究改进，设计了一种双混沌序列发生器，其原理图如2所示。

图2 双混沌序列发生器原理图

本文设计的双混沌序列发生器是由Logistic1发生器和Logistic2发生器通过迭代构成的，Logistic1定义为一级混沌序列发生器，Logistic2定义为二级混沌序列发生器，设定初始值分别作用在Logistic1发生器和Logistic2发生器上，使其分别产生相应的混沌序列。

整个双混沌序列发生器共有四个初始值x0，n1，n2，m0。它们的作用分别是：x0、n1作为Logistic1发生器的初值，使其能够正常生成初始化的混沌序列。m0的作用是控制Logistic1发生器由每个初始值所生成的混沌序列的个数，n2作为Logistic2发生器的初值，该双混沌序列发生器设计了两个特殊的操作功能，它们分别对应于双混沌序列发生器原理图中的两个盒子L1和L2。

L1的作用首先是存储Logistic1发生器由初值x0、n1生成的初始混沌序列，并且排列的顺序就是生成顺序，其次就是将其初始值m0与其信号相加，然后将其结果通过相应方式同样映射到［0，1］区间内，将上述操作之后的结果作为Logistic2发生器的下一个初始值x。

L2的作用是将L1中传出的［0，1］之间的数值进行存储，并对其数值除以10之后再加上3.9，将其得到的值作为Logistic2发生器的初值r。

由于伪随机序列是通过多次迭代产生的，同时根据Logistic映射可知，当其初始值发生微小的改变，想要对生成的混沌序列轨道发生巨大的差异改变，就必须进行多次迭代。所以说在对其混沌序列取值时，将生成的混沌序列前一段值删去，这样得到的混沌序列的初始值的敏感性会进一步增强。所以说，当产生混沌序列时，我们可以以第101个元素为起点进行取值，最后我们把值提取出来，让其作为X射线图像加密使用的混沌序列。

3 加密解密模块

在加密解密模块中，分别设计了X射线图像像素值的替代和X射线图像像素值的置乱，从而实现对X射线图像的加密目的。为了能使得X射线图像的加密效果达到更好，在加密解密模块中采用了多步X射线图像像素值替代和X射线图像像素值置乱的方法［9］，使其能更好地打乱X射线图像像素间的关系，从而更好的实现对X射线图像的加密。

设X射线图像某一点(i,j)处的图像灰度值为I(i,j)，且图像满足1≤i≤M 、1≤j≤N ，I′(i,j)表示为经过替换后I(i,j)在(i,j)处的图像灰度值。

1）X射线图像像素值替代公式：

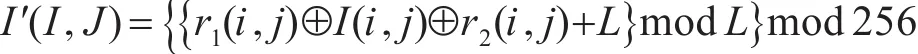
根据上面的式子我们知道：L代表了图像的颜色深度；mod代表了求模运算；⊕代表了按位异或的运算。r1，r2代表了混沌序列值，r1，r2代表了对应的混沌系统中替换变换的密钥，可以多次进行变换，从而达到更加好的加密效果。设重复的次数是n，密钥是混沌模型的初值与参数一起组合，密钥的空间得到了扩大，加密的强度得到了提高。

所以如果X射线图像很大，通过公式我们可以知道r1，r2模版矩阵需要随着它增大，这样就在很大的程度上降低了加密的效率。通过对X射线图像进行分快处理，也就是分块加密，加密的效果变好，效率得到提高。加密的逆就是解密，公式如下：

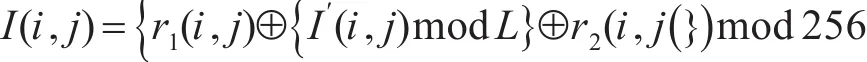
2）像素值置换公式如下：

根据上面的阐述，我们知道r1，r2都是混沌映射产生的，从像素值置换公式能够了解密钥，它包括：混沌模型的初值、混沌模型的参数，任意的正整数α，β，这样不但能够扩大了密钥空间的效果，而且加强了算法的安全性。加密运算的逆过程就是解密运算，以下就是解密过程实现。

4 实验结果及安全性分析

实验选取X射线检测两钢板之间焊缝的灰度图像进行仿真，图像大小为256×256。实验在Microsoft Windows 7系统下，处理器为：Pentium（R）Dual-Core CPU E6700，处理器频率为 3.20GHz，1G内存，使用Matbal7.0进行实验的，试验结果如图3所示。

输入正确的密钥后，对图像进行加密解密实验，其结果如图3所示。从图中可以看出从加密后的图像人眼无法识别，完全看不出原始图像的任何结构信息。加密后的图像杂乱无章，是一幅毫无纹理的图像，由此可知此加密效果很理想。

4.1 直方图分析

明文由于具有本身的特性，像素灰度值的分布一般来说都是不均匀的，当图像通过良好的加密算法进行加密后，其灰度值会在像素灰度值直方图中均匀分布。

如图4所示，直方图的横坐标代表图像的灰度值，直方图的纵坐标代表像素的个数，其左右两个直方图分别是代表该图像加密前和该图像解密后的，从直方图中可以看出其灰度值分布参差不齐，相邻像素间存在着很大的相关性［10］；其中间直方图代表密文图像直方图，图像经过加密后其灰度值的分布均匀稳定，由此可以判断本算法不仅能在很大程度上减小相邻像素之间的相关性并且使灰度值均匀的分布，从而体现了其抗统计分析的性能。

图4 灰度直方图的对比

4.2 加密算法的比较分析

本文混沌序列发生器设计的是双Logistic映射，是在单一Logistic映射的基础上进行改进研究的。所以可以进行实验来验证本算法的加密效果是否更加优良。

图5 加密算法对比图

图5 中，（a）图代表本文双Logistic映射控制加密的算法进行加密的结果图。（b）图是使用单一混沌映射（本文采用logistic映射）控制加密的算法进行加密的结果图。从图5（b）中隐约可以看出原始图像被无数条线段分割，且其纹理具有规则性，从而有可能被攻击者进行分析破译。在图5（a）中，则完全是一幅毫无规律可循、杂乱无章的图像，无法看出原始图像的痕迹。同时本文算法比单一混沌序列控制实现的算法密钥空间大很多，可以有效地抵抗群举攻击，因而有很强的安全性［11］。因此，从加密效果上来说，本算法结果还是能令人满意。

5 结语

针对混沌图像加密算法中的“有限精度”问题，Rowlands．T提出了“轨道跳跃”的思想，基于他的思想，许多学者提出不同的加密算法，但这些算法仍然存在许多不足。本文在对现有的算法进行改进的基础上，提出了一种较为复杂的双混沌序列发生器，本发生器在有效避免“有限精度”问题的同时，能够比较有效地提高迭代序列发生器的安全性。针对混沌图像加密算法单一、安全性不足的问题。本文深入研究了混沌序列生成置乱矩阵的方法，针对现有混沌象素置乱算法步骤较多，耗时较长的问题，对图像位置置乱算法进行改进，改进后的算法能比较有效地减少加密处理的时间。将其与象素置乱方法相结合，能够较好地实现混沌多步图像加密。基于以上的双混沌序列发生器和新的图像位置置乱算法，设计了一种双混沌图像多步加密系统，本系统由双混沌序列发生器产生混沌序列，经过混沌图像象素置乱和混沌图像位置置乱后得到加密图像。试验证明，本系统具有较高的初值敏感性、较强的安全性和较好的加密效果，可用于实际的图像加密系统。

［1］Jayanthi V E，Rajamani V.数字图像水印几何攻击性能分析［J］. 国际电子学报，2011，98（11）：565-1580.

Jayanthi V E，Rajamani V.Performance analysis for geometrical attack on digital image watermarking［J］.International Journal of Electronics，2011，98（11）：565-1580.

［2］王静，蒋国平.一种超混沌图像加密算法的安全性分析及其改进［J］.物理学报，2011，60（6）：26-29.

WANG Jing，JIANG Guoping.Study on security of hyperchaotic image encryption algorithm and its improvement［J］.Acta Physica Sinica，2011，60（6）：26-29.

［3］Biham E，Biryukov A.戴维斯对 DES攻击的改进［J］.Journal of Cryptology，1997，10（3）：195-205.Biham E，Biryukov A.An improvement of Davies'attack on DES［J］.Journal of Cryptology，1997，10（3）：195-205.

［4］黄润生.混沌及其应用［M］.武汉：武汉大学出版社，2000，15（5）：15-29.

HUANG Runsheng.Chaos and its application［M］.Wuhan：Wuhan University Press，2000，15（5）：15-29.

［5］王晓云，余洪波.如何打破MDS等散列函数［J］.计算机科学讲义，2005，34（94）：19-35.

WANGXiaoyun，YUHongbo.How to break MDSand other hash other functions［J］.Lecture Notes in Computer Science，2005，34（94）：19-35.

［6］王晓云，尹义群，余红波.在整个SHA-1中发现碰撞［J］.计算机科学讲义，2005，36（21）：17-36.

WANG Xiaoyun，YIN Yiqun，YU Hongbo.Finding collisions in the full SHA-1［J］.Lecture Notes in Computer Science，2005，36（21）：17-36.

［7］N K Pareek，Vinod Patidar，K K Sud.图像加密采用混沌逻辑映射［J］.Image and Vision Computer，2006，24（1）：926-934.

N K Pareek，Vinod Patidar，K K Sud.Image encryption using chaotic logictic map［J］.Image and Vision Computer，2006，24（1）：926-934.

［8］李树军，牟选奇，余红波.基于混沌系统的概率加密方案问题［J］.国际应用科学与工程分岔与混沌杂志，2003，13（10）：3063-3077.

LI Shujun，MOU Xuanqin，JI Zhen，et al.Problems with a probabilistic encryption scheme based on chaotic systems［J］.International Journal of Bifurcation and Chaos in Applied Sciences and Engineering，2003，13 （10） ：3063-3077.

［9］L Kocarev，JSzczepanski，JMAmigo等.离散混沌理论的研究［J］.常规论文，2006，53（6）：1300-1309.

L Kocarev，JSzczepanski，JMAmigo，et al.Discrete chaos-I：theory［J］.Regular Papers，2006，53 （6） ：1300-1309.

［10］JM Amigo，L Kocarev，JSzczepanski.离散 Lyapunov指数和抗差分密码分析［J］.Express Briefs，2007，54（10）：882-886.

JM Amigo，L Kocarev，JSzczepanski.Discrete Lyapounv exponent and resistance to differential cryptanalysis［J］.Exepress Briefs，2007，54（10）：882-886.

［11］GJakimoski，K PSubbalakshmi.离散Lyapunov指数和差分加密［J］.Express Briefs，2007，54（6）：499-501.

G Jakimoski，K P Subbalakshmi.Discrete Lyapounv exponent and differential cry ptasis［J］.Exepress Briefs，2007，54（6）：499-501.