基于永磁体标记的胶囊内镜旋转测量定位模型设计

李修寒，竺明月，印佳，殷悦，嵇敏洁，吴小玲南京医科大学生物医学工程系(南京，210029)

0 引言

电子计算机、 微机电系统、 新型材料的快速发展[1]， 为胶囊内镜的问世带来了契机[2]， 也为消化系统疾病的检查带来了新技术、 新方法[3]。现阶段， 不同的胶囊内镜生产厂家采用不同的定位技术， 而对于体内的目标定位根据原理的不同， 主要有：超声定位[4]、 光学定位[5]、 磁电式定位[6]等方法。在实际临床运用中， 上述的定位方法虽然技术成熟， 但是由于设备体积、 成本和使用复杂度等原因， 没能很好地在实际操作中推广。因此， 研究一种体积小、 使用简单、 成本低的定位技术成为国内外学者研究的热点。英国Glasgow等三所大学的研究人员首次采用磁标记物定位的方法研制了LAB-in-PILL系列的胶囊内镜， 虽然较大的体积没能在临床上得到广泛的应用， 但为磁定位的研究方向提供了一种新思路。

郭廷麟等[7]通过将磁体整合融入胶囊， 设计了手持式磁扫描内镜定位设备， 初步实现了对胶囊的模糊定位。何文辉[8]研制了人体胃肠道无创诊查系统， 并对系统中生物遥测胶囊的磁定位技术作了比较深入的研究。侯文生等[9]通过在微型药物释放装置上固定永磁体， 当其通过消化道时在体外检测磁场变化， 进而计算出微型药物释放装置的空间位置， 初步实现定位功能。

综上所述， 许多国内外的研究都从事于永磁体标记的定位方法， 证明磁标记定位方法是一种解决胶囊内镜定位的方案。在实际的研究探索过程中， 很多研究都需要使用大量传感器或者传感器阵列[10]的方式来提高定位精度。本课题组几年以来一直从事永磁体的定位工作， 已经通过少量磁传感器实现弱磁信号测量[11]、 磁靶向药物实时示踪[12]、 磁标记的三维步态分析[13]等工作， 发现在磁定位系统定位精度的影响因素方面， 除了提高传感器精度、 改进信号处理电路和定位算法之外， 还可以通过磁传感器旋转检测的方式实现进一步的优化和改进。

本文提出并设计了利用GF708磁传感器[14]旋转定位方式， 通过建立旋转检测的理论模型， 从而相对降低了信号处理的难度， 简化了算法的复杂程度， 实现了对单个圆柱体永磁体的定位。

1 方法

1.1 环形电流的空间磁场分布

在计算圆柱型永磁体的空间磁场分布时，一般会把永磁体的磁场看作为永磁体内部若干排列整齐的分子电流共同激发产生[15]，假定永磁体被均匀磁化，那么永磁体内部的分子电流效应将会相互抵消，永磁体的磁场来源可被视为仅存在于永磁体表面的环形电流[16]。

根据Biot-Savart定律，环形电流在空间一点p产生的磁通密度为：

(1)

经近似化简并对磁通密度分布进行积分，得到环形电流对空间任一点 磁感应强度为：

(2)

(3)

(4)

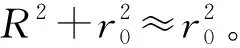
1.2 圆柱体永磁体的空间磁场分布

根据上述环形电流的空间磁场分布，可以将圆柱体永磁体看作成拥有环形电流的圆形薄片，如图1所示。

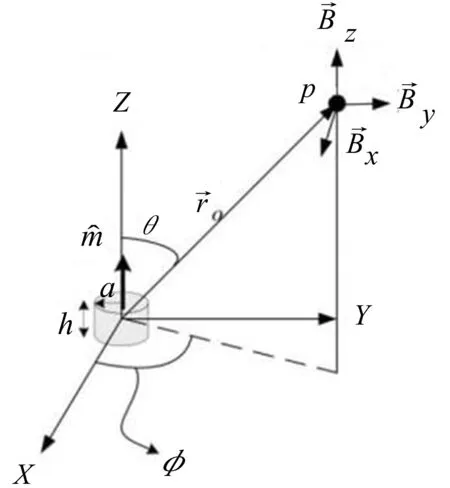
图1 圆柱体永磁空间场坐标示意图Fig.1 Cylindrical permanent magnet space coordinate diagram

将此时的体磁偶极矩定义为Mr=πa2hM0(Am2)，当r0≫a和r0≫h时得到如下近似：

(5)

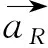
1.3 旋转测量的永磁体定位模型建立

旋转测量的永磁体定位模型，如图2所示。

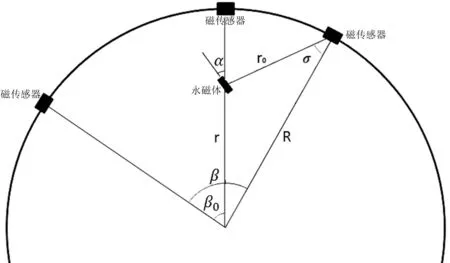
图2 旋转定位模型平面示意图Fig.2 Rotational positioning model plane schematic

其中β表示传感器在旋转的过程中距离初始位置的夹角，β0用于表示传感器的初始位置，R表示传感器旋转的半径，建立此极坐标系，得到基于扫描定位的磁场强度模型。

当考虑永磁体、 磁传感器位于同一旋转平面内，合磁场方向沿θ方向，合场强为：

(6)

磁偶极子模型中的r0，为永磁体到传感器之间的距离，在平面内根据余弦定理可以得到。因此，平面中永磁体位于某一点p时，在扫描一周得到的磁场大小为：

(7)

GF708磁传感器测量的磁场大小与夹角σ的余弦成正比关系，得到：

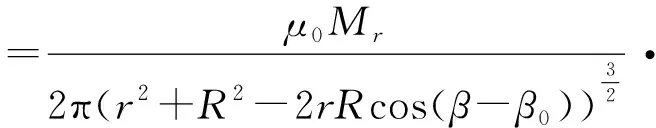
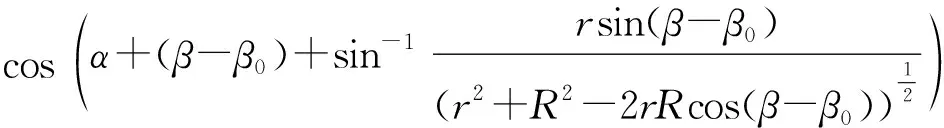
(8)

当圆柱体永磁体轴线不平行于旋转的传感器平面时，需要引入新的变量：用δ来表示永磁体与所在平面构成的夹角，其关系满足M=Mrcosδ，该运算就是将磁矩Mr投影到平面上。得到：

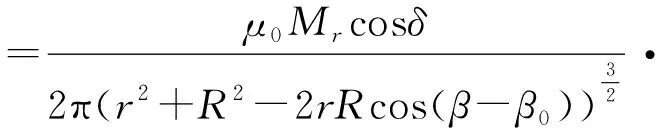
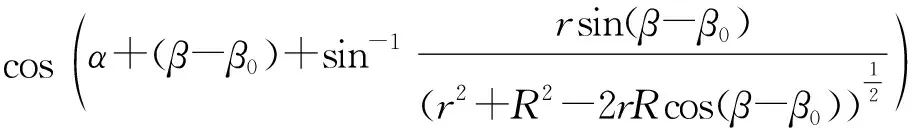
(9)

2 实验及结果

2.1 旋转定位模型的验证

本文选用直径5 mm，高度10 mm的永磁体，利用高斯计测量永磁体磁场强度，根据磁场强度与磁矩的关系[17]并计算，得到此永磁体磁矩为0.436(A·m2)。

模型验证采用单个永磁体水平放置，将圆柱体永磁体的轴向方向正对传感器的轴向方向，通过旋转模型和传感器参数可以得到传感器两端电压大小与实际测量的磁场强度关系：

U=V·S·F·B测

(10)

其中U为传感器两端电压，V为供电电压，S为传感器灵敏度典型值，F为系统电路放大倍数。

为了更加直观地看出模型与实际情况的差异，实验时将永磁体水平放置在传感器的轴向方向，此时公式中仅有一个未知数r，则电压与永磁体距离之间的关系可以改写为：

(11)

通过将测量的电压值同理论数值的比较，可以验证模型的科学性。实验测量的数值同模型理论计算的数值通过MATLAB软件比较如图3所示。

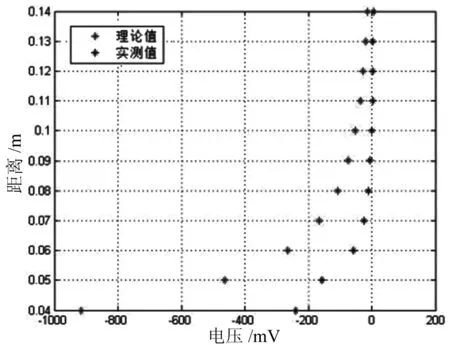
图3 模型理论电压同实测比较图Fig.3 Comparison chart of model theorywith the measured voltage

从图3中的趋势来看，模型具有一定的科学性，但还存在很大的误差。考虑模型本身可能存在问题之外，传感器本身可能存在个体差异，即在不同供电电压下，可能存在诸多因素导致误差。因此，我们通过MATLAB函数拟合，针对上述实测数据对当时环境下建立的模型做了两个参数的修正，修正后的计算公式为：

(12)

通过修正系数a控制了模型同实际测量之间的漂移差异(下文称为初值修正)，通过修正系数b调整了传感器在不同工作环境下灵敏度的差异(下文成为倍数修正)。通过MATLAB分析，对模型的初次修正为a=0.043，b=0.158。修正后的模型计算数值同实验测量的数值通过MATLAB软件比较如图4所示。

图4 修正后模型理论电压同实测电压比较Fig.4 The corrected model theoretical voltageis compared with the measured voltage

从图4中观察到，在永磁体距离传感器距离超过7 cm时，模型计算得到的电压数值同实测数据之间的误差在可以接受的范围内。但是在7 cm之内的误差很大，其误差无法通过修正弥补，是由于模型本身缺陷产生的。

2.2 定位结果及误差分析

经过上文对模型的验证以及针对传感器本身和永磁体差异性的修正后，下文进行了两个方面的定位实验。

2.2.1圆柱体永磁体位于传感器初始位置的轴线上

当圆柱的轴线同传感器不在同一轴线上，呈一定夹角，且永磁体仍然处于传感器初始位置的轴线上，此时定位需要求解两个定位未知数，为永磁体中心与旋转圆心距离r和永磁体轴线与直径夹角α。

传感器采集了北偏西60°(300°)、 正北(0°)、 北偏东60°(60°)三个位置的电压数据，传感器的初值分别为-5.65 mV、 -6.91 mV、 -5.66 mV，传感器的旋转半径为14.6 cm，其中初值修正为0.91，倍数修正为0.066 7。

实验首先控制永磁体与圆心的距离r改变，永磁体轴向同直径角度α不变进行实验，定位数据如表1所示。

表1中的U1、U2、U3为北偏西60°(300°)、 正北(0°)、 北偏东60°(60°)的电压数据。该组实验中仅改变了永磁体距离圆心的距离r，没有改变永磁体与直径的夹角α。通过表1左侧的电压数据可以计算得出，定位的距离r平均误差为0.24 cm，角度α的平均误差为0.141 rad。

表1 定角度变距离实验数据Tab.1 Fixed angle variable distance experimental data

控制永磁体与圆心的距离r不变，改变永磁体轴向同直径角度α进行实验，实验数据如表2所示，其中传感器的初值分别为-5.65 mV、 -6.91 mV、 -5.66 mV，传感器的旋转半径为14.6 cm，修正参数中初值修正改为0.2，倍数修正为0.066 7。

由于第二组数据选择了永磁体与圆心距离不变，改变永磁体轴向同直径之间的角度的方式进行实验，在运算结果前对定位模型中的修正参数实施微调，且选取测试的距离为4.6 cm，为第一组实验中综合误差最小的位置，在最终求解的过程中，距离r平均误差为0.08 cm，角度α的平均误差为0.057 rad。

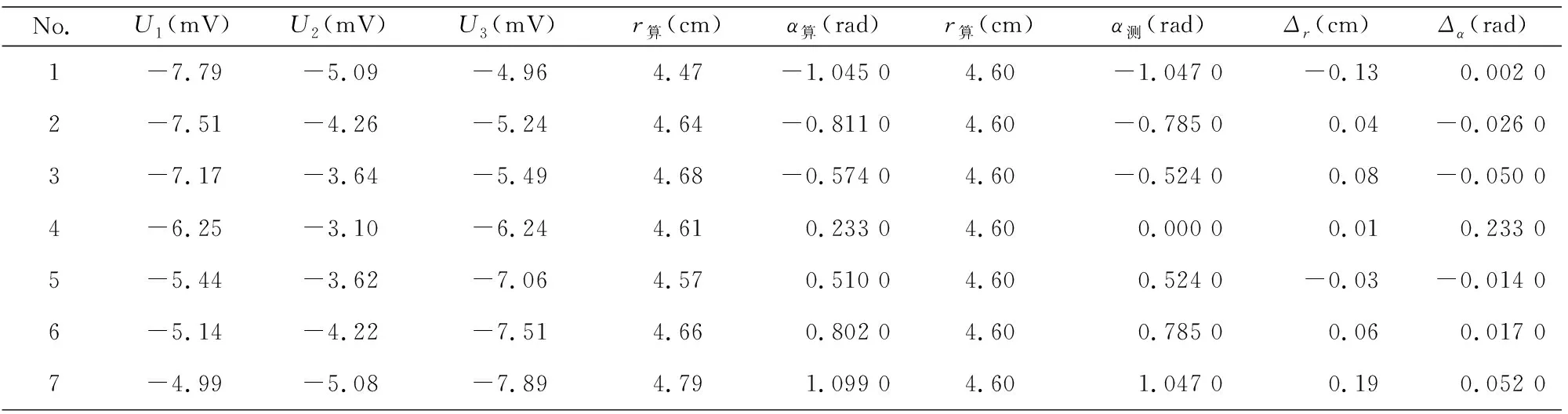
表2 定距离变角度实验数据Tab.2 Variable distance from the experimental data

2.2.2圆柱体永磁体位于平面内随机位置

当圆柱永磁体位于平面内随机位置时，系统则需要使用三个未知参数来求解永磁体的位置及角度，未知数分别为：磁体距离圆心r，永磁体所在半径与正北方向的偏转角 ，永磁体轴向同所在半径所成夹角α。

传感器的初始位置为地磁场正北方向，那么定位永磁体位置需要使用(r,α,β)表示其在平面中的位置，使用α表示永磁体轴向同直径的夹角，那么模型需要求解这三个未知量来实现定位。因此实验选择了随机的几个不同的位置来实施定位实验，旋转测量数据如表3所示，求解、 实测结果及误差如表4所示。其中传感器的初值分别为-5.65 mV、 -6.91 mV、 -5.66 mV，传感器的旋转半径为14.6 cm，修正参数中初值修正为0.17，倍数修正为0.066 7。

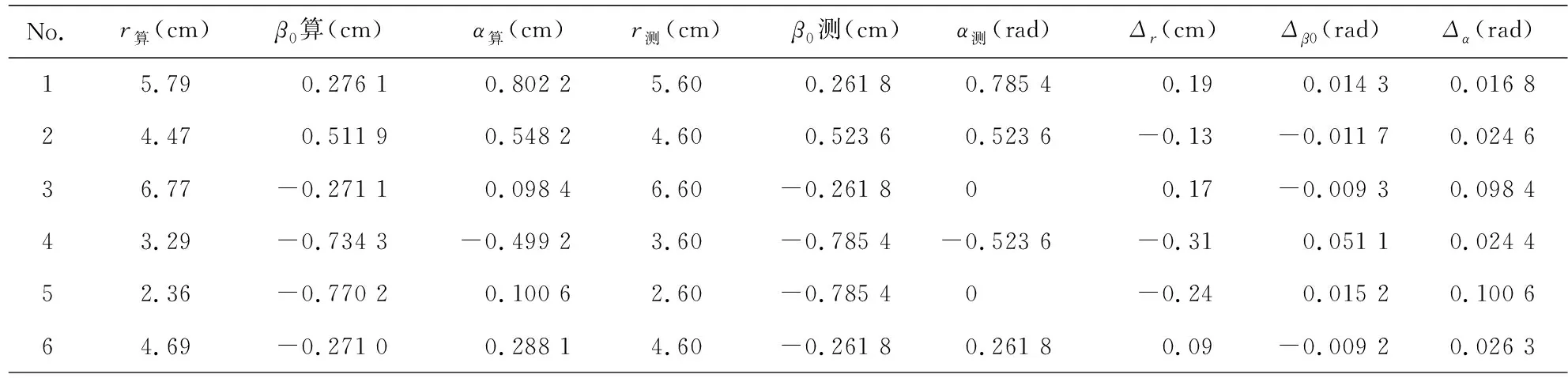
表3 永磁体随机定位实验结果及误差Tab.3 Experimental results and errors of random positioning of permanent magnets

通过表3数据可以计算出在旋转平面内随机位置及角度的摆放圆柱体永磁体，磁体距离圆心r平均误差为0.19 cm，永磁体所在半径与正北方向的偏转角β的平均误差为0.019 rad，永磁体轴向同所在半径所成夹角α的平均误差为0.049 rad。

3 结论

本文通过建立了全新的旋转定位模型， 减少了在实际运算过程中的未知数数量， 通过简化现有模型达到降低误差的目的。通过旋转解决了其非三轴传感器无法对空间进行运算的缺陷， 最终达到了仅通过单轴的传感器的磁场强度测量求解目标位置的定位目的。为实现人体内胶囊内镜的定位奠定理论基础。

在未来， 旋转定位的方式还可能用于两个甚至多个磁目标的定位， 还可以通过增加传感器的数量来达到不旋转即能够利用本系统模型定位的目的。

[1] Menciassi C S, Gorini S, Pemofio G, et al. Locomotion of a legged capsule in the gastrointestinal tract[C]. Theoretical study and preliminary technological results. In Proceedings of the26th Annual International Conference of the IEEE EMBS September1-5,2004. San Francisco. CA, USA.

[2] 顾元婷,廖专,李兆申,等.磁控胶囊内镜研究和应用进展[J].中华消化内镜杂志,2017,34(2):143-145.

[3] 张晓岚,郭金波,韩菲,等.2016年消化系统疾病主要临床进展[J].临床荟萃,2017,32(2):121-131.

[4] 高立明,颜国正,戎荣.新型自动植入式医用内窥镜的研究[J]. 高技术通讯,1998,10:57-60.

[5] Phee L, Accoto D. Analysis and development of locomotion devices for the gastrointestinal tract [J], IEEE Trans Biomed Eng,2002,49(6):613-616.

[6] NDI公司.AURORA电磁跟踪系统技术手册[R].CANADA.

[7] 郭廷麟,辛磊,邹文斌,等.ANKON胶囊内镜磁扫描定位技术的初步研究[J].中华消化内镜杂志,2013,30(12):701-702.

[8] 何文辉.人体胃肠道无创诊查系统及生物遥测胶囊磁定位技术与实验[D].上海：上海交通大学,2007.

[9] 侯文生,郑小林,彭承琳,等.基于磁定位的消化道微型药物释放装置动态跟踪技术研究[J].北京生物医学工程,2005(1):36-38.

[10] 任宇鹏,胡超,项圣,等.一种人体移动对胶囊内窥镜磁定位干扰的补偿方法[J].传感技术学报,2015(11):1640-1646.

[11] 王旋,敦煌俊秋,汤福南,等.基于磁定位技术的放疗呼吸曲线检测系统的设计与应用[J].中国医疗设备,2015(6):42-45,32.

[12] 王延花,王旋,敦煌俊秋,等.基于磁阻传感器的磁靶向药物实时示踪系统设计[J]. 南京医科大学学报(自然科学版),2014,34(9):1206-1212.

[13] 张可,汤福南,李修寒,等.基于永磁定位技术的三维腿部运动检测系统设计[J].中国医疗设备,2017,32(9):33-39.

[14] 德国sensitec公司.GF708系列传感器数据手册[R].2015.

[15] 任家峪.基于磁传感器阵列的无线跟踪定位技术及其应用研究[D].重庆：重庆大学,2010.

[16] 刘金寿,戎绍金.电流环与磁偶极子等效变换中的磁荷计算[J].辽宁师范大学学报(自然科学版),2003,26(4):442-443.

[17] 李子芳.永磁体等效磁矩的测量[J].大学物理实验,1994,7(2):5-8.