单粒子软错误的数值仿真技术
毕津顺
(1. 中国科学院微电子研究所, 北京 100029; 2. 中国科学院大学 微电子学院, 北京 10049)
辐射效应是电子器件和材料在辐射场(例如,空间辐射环境等)中的性能变化的表现,包括总剂量效应、位移损伤效应和单粒子效应等。不同来源的统计数据表明,有16%~42%的航天器故障和异常是由空间环境引起的。据AEROSPACE公司1999年的统计表明,在导致航天器异常或故障的空间环境效应中,各种辐射效应占88%,其中,总剂量效应占5.4%,表面充电效应占20.1%,深层充电效应占24.7%(难以辨别的充电效应占9.4%),单粒子效应占28.4%[1-5]。到目前为止,单粒子效应是诱发航天器异常或故障最多的辐射效应。下面分别简要介绍总剂量效应、高剂量率瞬态辐射效应和位移损伤效应。
总剂量效应全称“总电离剂量效应”,是大量的辐射粒子进入半导体器件材料内部,与材料的原子核外电子发生电离作用产生额外的电荷,这些电荷在器件内的氧化层累积,或者在Si/SiO2界面诱发界面态,导致器件性能逐步退化。这是一个长期累积的过程,表现为电流和阈值电压等参数漂移,电路的静态功耗显著增加或功能发生失效等[6-10]。高剂量率瞬态辐照效应,是指很高剂量率(如107~1010Gy(Si)·s-1)的瞬态γ、X射线产生的高密度流电子-空穴对在电场作用下分别趋向正极和负极,形成光电流,造成逻辑功能混乱、闩锁或烧毁,导致电路半永久性或永久性失效[11-13]。
位移损伤效应有别于“总电离剂量效应”,也称为“非电离能量损失效应”(non ionizing energy loss,NIEL),是大量的辐射粒子(主要包括质子、电子以及次级粒子)进入半导体器件材料内部,与材料中晶格原子发生弹性碰撞作用,若在碰撞中传递给初冲原子(PKA)的动能超过移位能(产生一个Frenkle对所需要的最小能量),则PKA会离开原来的位置,导致材料晶格原子出现移位,最终使器件材料内部产生稳定的复合缺陷,影响少数载流子寿命,从而导致器件相关性能逐步下降乃至最终丧失的现象[14-15]。
1 单粒子效应
随着单粒子效应研究的不断深入,新器件的不断应用,新现象的不断出现,单粒子效应分类越来越细。表1给出了目前已经明确定义的单粒子效应类型。所有这些效应中,单粒子烧毁、单粒子栅穿、单粒子位移损伤和单个位硬错误都为永久损伤,也称硬错误,通过重新写入或断开电源,被辐射器件仍然不能恢复正常状态,器件彻底损坏。此外,单粒子闩锁在不采取保护措施的情况下,也会导致永久损伤。其他单粒子效应均为软错误,器件可以恢复正常状态。总的来说,无论是永久性错误还是软错误,对于运行中的航天器来说,任何一种效应都可能导致重大事故和巨大损失。

表1 单粒子效应分类[16-21]Tab.1 Categories of single-event-effects
2 单粒子软错误
单粒子软错误主要发生于存储器件和组合/时序逻辑电路中,是入射粒子运动径迹周围产生的电荷被灵敏电极收集,形成瞬态电流,触发逻辑电路,导致逻辑状态翻转[22-24]。当粒子穿过芯片时,粒子损失能量,并沿其路径激发电子-空穴对,这些电荷能够通过漂移和扩散机制被反偏PN结收集,而关态晶体管的漏结是反偏的,所以它能够收集电荷。如果反偏漏结收集到足够多的电荷,相应节点的电压将会发生变化。这种效应通常并不对电路造成损坏,因此是一种软错误。如果电路电压改变不能很快恢复,这一脉冲电流将会引起电路系统很长时间的混乱。尤其是如果电路中收集的电荷不能在反馈引起单元翻转前消散,存储在SRAM单元中的逻辑值就将发生改变,芯片中存储单元的错误可能会导致系统错误[25-26]。
现有的单粒子软错误的物理过程分为电荷淀积和电荷收集两个过程,下面介绍这两个过程的基本机理[27-28]。
2.1 电荷淀积
在半导体器件中存在两个主要电离辐射释放电荷的模式:1)入射粒子直接电离;2)由于入射粒子与器件作用发生核反应产生的次级粒子发生的间接电离。这两种机制同时产生并作用在受到粒子辐射的器件中。
2.1.1 直接电离
当高能带电粒子穿过半导体材料时,损失能量,沿着入射路径离化产生电子空穴对。有效电荷为Zeff的反冲离子和硅原子外层电子发生库仑作用,引起电离,产生了高能电子(δ射线),通过进一步离化或者在1~100 fs时长内激活光子从而失去能量。最终,在硅中产生一个自由电子-空穴对所需的平均能量是3.6 eV(1 eV=10-19J)。能量转移(LET)指在单位路径上淀积的能量,MeV·cm-2·mg-1,描述了离子穿过材料时单位路径上的平均能量损失。LET值的单位也可为pC·μm-1或fC·μm-1,这种单位更适合于电路设计人员,因为可以直接与器件物理尺寸以及关键结点存储电荷进行比较。
如果初始能量大于Bragg峰能量,则沿着入射路径LET先增加,直至能量衰减至Bragg峰能量,然后LET值逐渐降低。这个效应对于保护层而言非常重要。如果保护层的厚度不足以阻止入射粒子,则敏感结点处的LET值有可能在有保护层的情况下要大于没有保护层的情况。
质子即氢核,其Bragg峰值能量很低,在50 keV附近。质子在Bragg峰处的LET值为5.5 fC·μm-1,然后在500 keV处迅速衰减到2.6 fC·μm-1,在1 MeV处达到1.8 fC·μm-1。所以,当入射深度大于200 nm,并且电路临界电荷小于1 fC,低能质子可以通过直接电离机制引发单粒子翻转。
图1给出210 MeV 的Cl粒子入射到Si中,LET值随着入射深度而发生变化,这说明粒子产生的电荷淀积也是入射深度的函数。电荷淀积有一个Bragg峰,通常入射粒子能量衰减到每核子1 MeV时产生Bragg峰。一个经验的说法是粒子最大LET值和它的原子序数Z大致相当。重离子发生直接电离辐照,产生电荷淀积导致翻转。
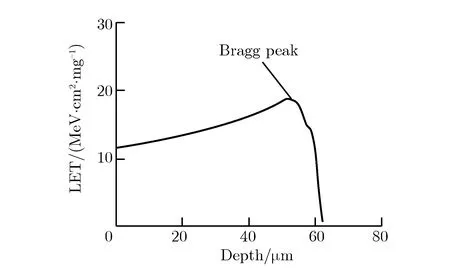
图1 210 MeV Cl粒子入射到Si中,LET值随入射深度的变化Fig.1 LET values vs. injection depth when 210 MeV Cl ion hits silicon
直接电离是引起单粒子翻转的主要机制,通常由于重离子撞击引起。所谓重离子是指原子序数≥2的离子(质子、电子、中子和介子除外),而轻粒子如质子直接电离辐照大多不能够产生足够导致翻转的电荷。然而近年来随着器件尺寸的不断缩小,质子通过直接电离辐照也有可能产生足够的电荷导致翻转。
2.1.2 间接电离
间接电离是指入射粒子与半导体材料发生核反应而产生的次级粒子的过程,这些核反应产物(包括反冲核,裂变核和α、γ粒子等)往往会产生新的粒子,它们可能比初级粒子含有更高的LET值,因而次级粒子的电离会淀积更高的电荷量,对单粒子翻转效应的贡献不容忽视。
对于100 MeV的中子,考虑非弹性碰撞下的28Si反冲。90%的硅反冲能量低于2.5 MeV,99%的硅反冲能量低于5 MeV。但是轻粒子,例如α粒子,能量较高。对于100 MeV的中子,10%的轻粒子反冲能量大于16 MeV,1%的轻粒子反冲能量大于31 MeV。
当En为20 MeV,发生的反冲物分成轻反冲物和重反冲物。轻反冲物包括质子(n,p),氘核(n,d),氚核(n,t),3He,4He(n,α)等;重反冲物包括21Ne,27Al,28Al,24Mg,25Mg,26Mg,28Si和24Na。不会产生原子序数在5~21之间的反冲物。对于更高的能量,会出现原子序数1~28之间的多数的同位素。
为了建立预测工具,计算电子器件的敏感度,最重要的步骤之一是构建核数据库。当一次核反应产生多个粒子时,核数据库也给出了这些粒子的发射角度。这些粒子的能量和发射方向与入射中子的能量以及方向有关。
在一个完整的核数据库中,所有材料中的反冲物,只要到敏感区域的距离小于反冲物的最大射程,都会记入考量。特别需要考虑,来自于SiO2中氧的反冲物,W塞中钨的反冲物,Cu互联的反冲物,以及MOS晶体管栅极高K介质的反冲物。它们对于器件软错误率的影响与采用的工艺密切相关,如金属层的厚度和数量,以及单元结构等。一个重要的问题是,如何使用数据库中产生的大量数据,计算电子器件的敏感度。
核反应中产生了不同的反冲物,从质子、中子到靶原子核。通常不考虑反应中生成的中子,因为它们在产生地附近发生反应的概率非常小。这些离子通过和靶原子电子发生库仑作用而损失能量,并在射程的尾端与靶原子发生弹性碰撞。
SRIM 和MSTAR 等程序给出了能量损失与入射中子能量之间的关系。最重要的参数包括离子的总射程或投影射程、单位长度上的能量损失、离子速率以及沿离化路径上的横向电离电荷密度分布。离子射程确定了敏感结点附近的有效体积,在有效体积内中子反应产生的反冲物有可能到达敏感结点。单位长度上的能量损失给出了电子-空穴对的密度,这些在空间电荷层以及PN结扩散长度范围内的电子-空穴对会被收集。横向电离电荷密度分布通常用来和结宽度或器件沟道长度进行比较。
必须区分轻离子和重离子:轻离子,如α粒子和质子,能量高而射程长;重离子,如Si离子、Al离子和Mg离子,能量低而射程短。利用SRIM2008计算了在硅晶格中,能量小于10 MeV的硅反冲的射程,如图2所示。当能量小于5 MeV时,射程小于3 μm。可以看出,射程虽短,但仍远大于目前工艺节点晶体管的尺寸,即使是重离子反冲也能到达多个敏感结点。

图2 在硅晶格中,硅的反冲射程Fig.2 Injection depth of silicon recoil in silicon lattice
2.2 电荷收集
在单粒子效应损伤机理的研究过程中,人们发现在器件的灵敏区收集到的电荷比耗尽区因漂移和浓度梯度引起的扩散收集到的电荷要多很多。因此提出过很多新的电荷收集模型,如电荷漏斗模型,粒子分流模型,电荷横向迁移模型等,其中电荷漏斗模型最为典型,理论也比较成熟,更易于现象的解释,如图3的示意图,其机理如下:
当粒子入射半导体器件,对于体硅工艺器件,最敏感的区域通常是反向偏置的PN结。反向偏置的PN结耗尽区的高电场通过漂移机制有效地收集入射粒子产生的电荷,进而产生瞬态电流。如果粒子入射位置靠近耗尽区则会导致明显的瞬态电流,因为产生电荷将会扩散到耗尽区,被有效收集。
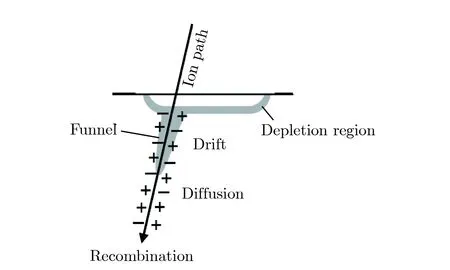
图3 粒子撞击PN结后扩散、漂移、复合和漏斗示意图Fig.3 Illustration of diffusion, drift, recombination and funnel after heavy ion strikes PN junction
如图4所示,由于入射粒子路径高电导特性和耗尽区电场分离,并离化产生电荷,粒子入射路径产生电荷会导致结电场局部塌陷。漏斗效应拓展了结电场,使之更深入衬底,即使距离PN结较远的电荷也可以通过漂移机制被有效收集,从而增加了入射节点的电荷收集。
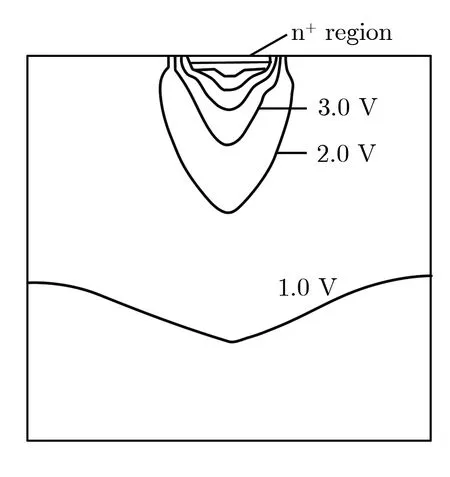
(a) Electrical potential
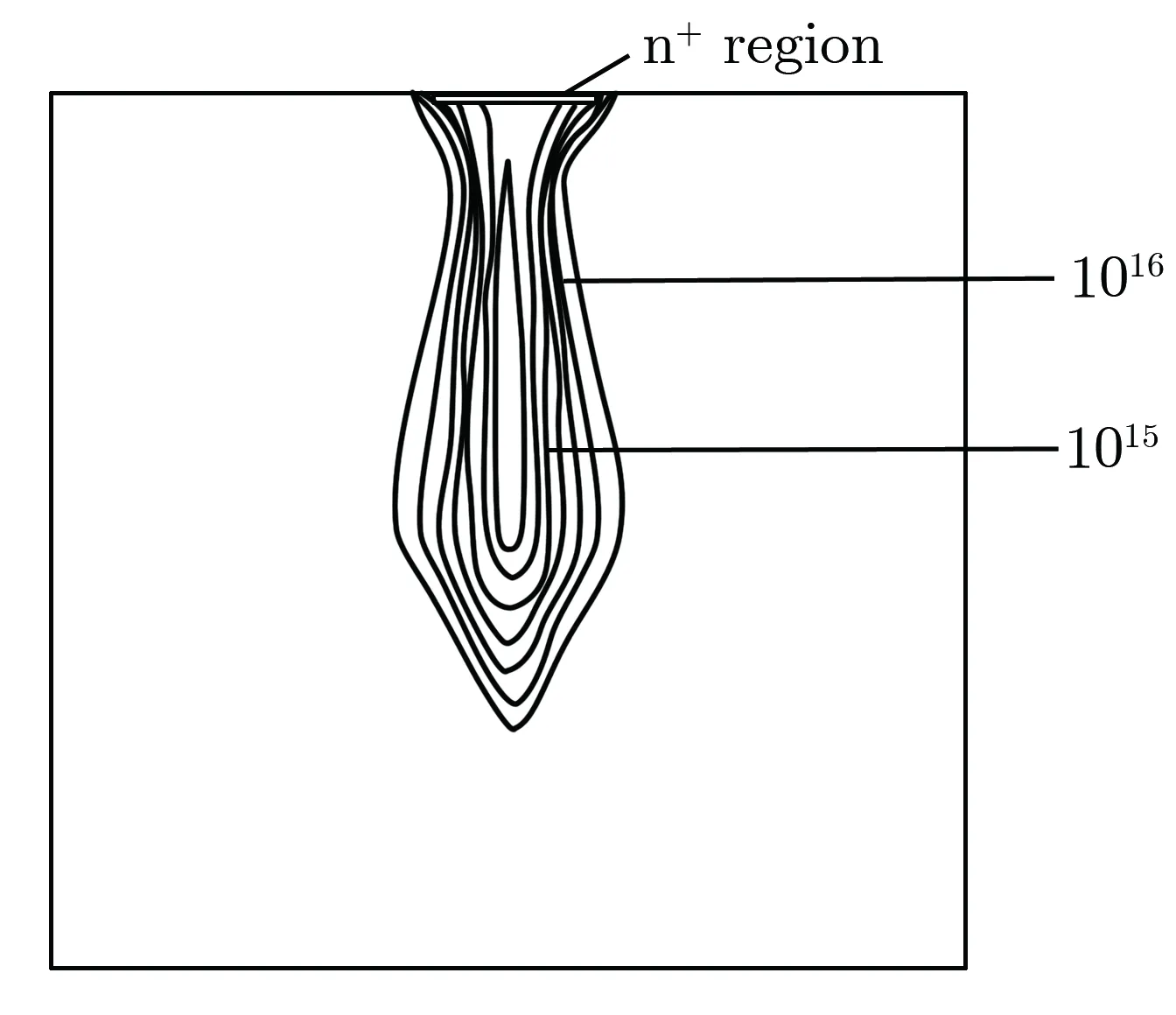
(b) Electron concentration
图4粒子撞击后n+/p结产生的漏斗
Fig.4Funnelinducedbyheavyionstrikingn+/pjunction
漏斗效应有如下特点:1)由于没有一个好的长度定义用于从一个物理点延伸漏斗,漏斗长度只是一个相对有用的概念用于计算错误率,可用于计算有源区和漏斗区收集的电荷;2)漏斗辅助漂移电流从而收集电荷,产生“光脉冲”电流。当衬底轻掺杂时,漏斗可持续很长时间;3)漏斗不仅由粒子垂直入射耗尽区引起,当粒子撞击耗尽区附近,足够高的载流子浓度扩散到耗尽区同样可以引起漏斗效应;4)当漏斗延伸到外延衬底二极管,会被外延层下重掺杂的衬底限制。一旦足够的载流子从外延层流出,耗尽层将恢复原状,漏斗效应停止,电荷收集的速率变慢,如图5中,n+/p外延二极管电荷收集会趋于一个常数,此时表明漏斗效应很弱;5)由于电子和空穴的迁移率不同,漏斗通常发生于n+/p二极管,而p+/n漏斗效应要弱很多,或者不会发生。这就是图5中p+/n曲线没有明显的电荷收集放缓点的原因;6)外延二极管收集的总电荷数应该近似等于外延中释放的电荷加外延衬底边界沿扩散长度淀积的电荷。漏斗影响外延层中淀积电荷的收集速度,但是不影响电荷收集的总量,因为即使没有漏斗效应,电荷最终也会被收集。
沿离化路径的电子-空穴对密度初始半径的变化,是半导体仿真程序的重要输入信息,用于计算敏感结点的收集电荷。通常认为,沿径向呈高斯分布,并且随着时间而不断展宽。过去器件的尺寸为微米量级,不需要精确知道1/e2处的离化半径。然而对于60 nm或者45 nm的设计规则,必须知道精确的离化半径变化。自由载流子产生发生在离子入射之后(速率和离子质量/能量相关)。通常认为载流子产生时间远小于器件的响应时间,所以近似认为载流子产生是瞬时发生的。
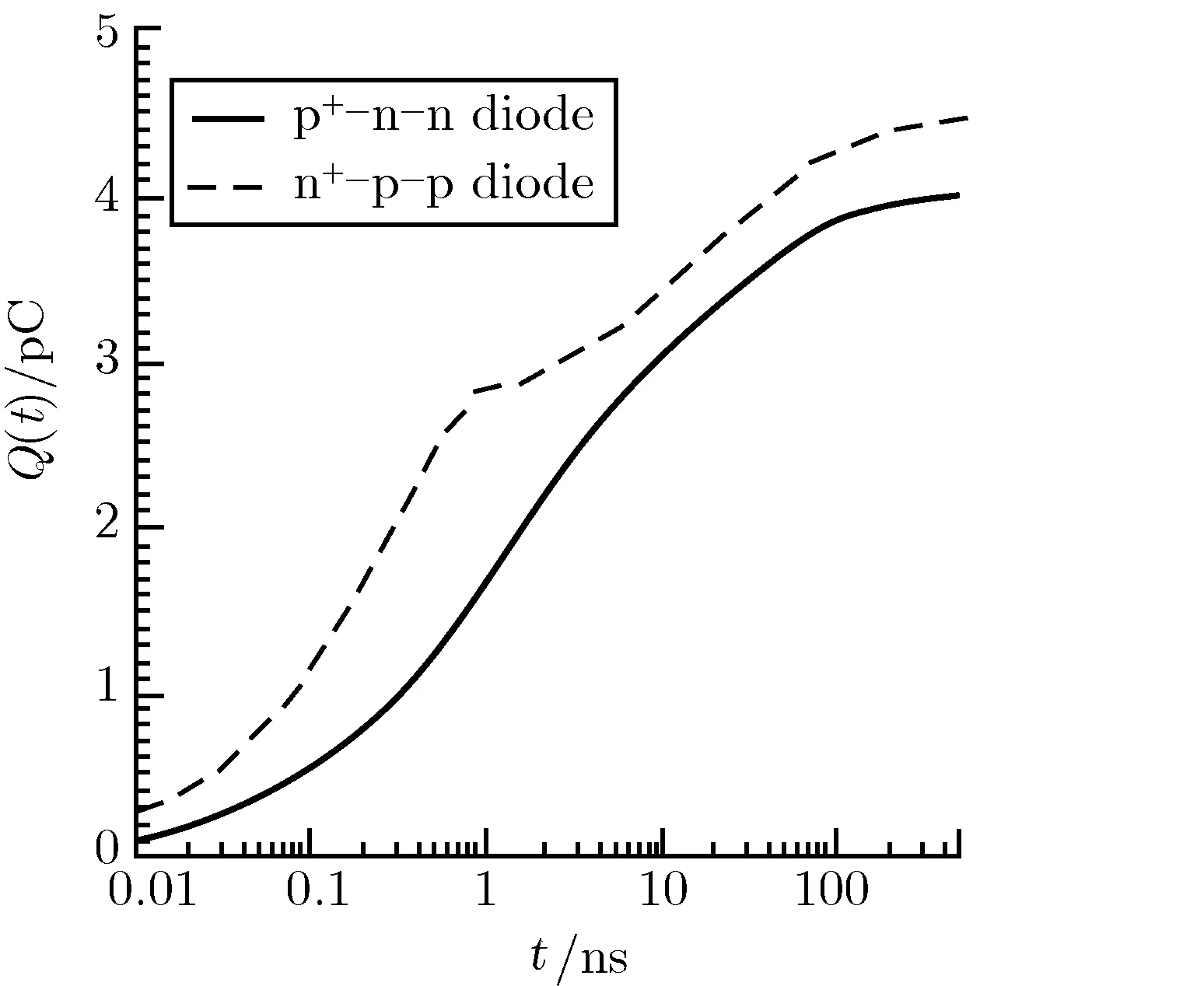
图5 粒子撞击n+/p和p+/n外 延二极管后电荷收集瞬态Fig.5 Transient charge collection after heavy ion strikes n+/p and p+/n epi-diodes
随着器件尺寸的减小,半导体器件进入了深亚微米甚至纳米时代,人们又发现了一些新效应,影响电荷的收集,主要有双极放大效应、ALPN效应、电荷共享效应和脉冲湮灭等,并且逻辑电路中的单粒子瞬态问题和存储电路中的多位翻转问题越来越严重。
2.3 粒子软错误的基本计算
2.3.1 临界电荷的标准
必须定义一个参数描述器件的敏感度,从而能够较为简单地评估入射粒子对于电路功能的影响。最简单的参数是特定结点的收集电荷,并与导致功能翻转的所需的最小电荷量进行比较。该最小电荷量称之为临界电荷。
可以简单地认为,临界电荷是结点总电容Ci与电源电压Vdd之积,即Qc=Ci×Vdd。该方法非常有效,可以粗略估算临界电荷。在近似估算中,认为电荷的收集是瞬时发生的,电路的其他部分没有时间响应。在某些情况下,该近似是错误的,比如通过扩散机制的电荷收集。
以反相器为例,在电荷收集的时间范围内,开态的晶体管将会提供电流,从而补偿收集电流。可以采用SPICE等电路仿真器更加准确地获得临界电荷。通常在敏感结点上施加双指数电流源,其对时间的积分即为临界电荷。
但是该电流脉冲峰值与敏感结点电压无关,所以上述模型不能够准确描述自由载流子收集以及与电压的函数关系。最好的方法是基于器件仿真器的全3D电路(例如6T SRAM单元)模拟或者混合模式仿真。当然这更加复杂且耗时。在混合模式仿真中,仅有一个晶体管用器件仿真器来描述,而其他晶体管则由电路仿真来描述。
积分流经PN结的瞬态电流脉冲,从而得到收集电荷。积分的时间限与电路翻转模式有关。如果电路没有发生翻转,则积分的时间限为恢复时间;如果电路发生翻转,则积分的时间限为翻转时间。对于方波,临界电荷是电流脉冲宽度的函数,如图6所示。
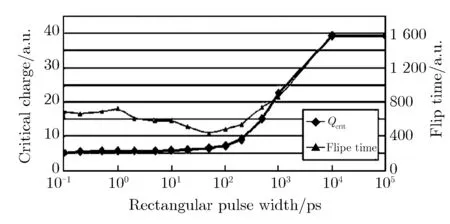
图6 临界电荷与翻转时间是脉冲宽度的函数,对于该工艺节点,脉冲宽度大于100 ps 后临界电荷与翻转时间开始增大Fig.6 Variation of the critical charge and the flip time as a function of pulse duration. For this particular technology node, the critical charge and flip time increase for t > 100 ps
电路结点总电容与工艺技术相关。在CMOS工艺中,结点电容主要是漏-衬底电容和栅-漏电容之和。如下文所述,现代工艺的SRAM器件的临界电荷约为1~2 fC。由于灵敏放大器的限制,DRAM和SDRAM的临界电荷近似保持恒定,在20~30 fC之间。
2.3.2 单粒子软错误截面
单粒子软错误发生的概率通常用翻转截面来表示,定义如下公式所示:
σ=N/φ
式中,σ为单粒子软错误的截面,cm2;N为器件发生某一种效应的次数;φ为单位面积入射粒子数,cm-2。截面越大,器件抗单粒子效应的能力越差。为了比较不同集成度的器件抗单粒子效应水平,定义位截面为总截面除以总单元数,表示每个单元发生单粒子软错误的概率。单粒子软错误的截面大小既依赖于入射粒子的种类和能量,又依赖于器件发生单粒子效应的临界电荷,也就是依赖于器件类型、工艺结构、集成度和偏置电压等,其经验公式如下:
Q=0.010 35×ELET×l
式中:l为入射粒子在电荷收集区域的有效路径,0.010 35为经验系数。
通常是测量截面 (每单位通量所测到的翻转个数)随有效LET值(离子的线性能量传输值除以入射束流表面夹角的余弦值)的变化关系曲线来表示某器件的抗单粒子能力,如图7所示。利用这种测量的曲线,再通过相关的模拟计算,可以评价和预估电子器件在空间辐射环境中的易损性。在图7中,当截面迅速增大时对应的那个LET值即为临界LET阈值,随着重离子LET的增大,截面不再增加时的截面即为饱和截面。
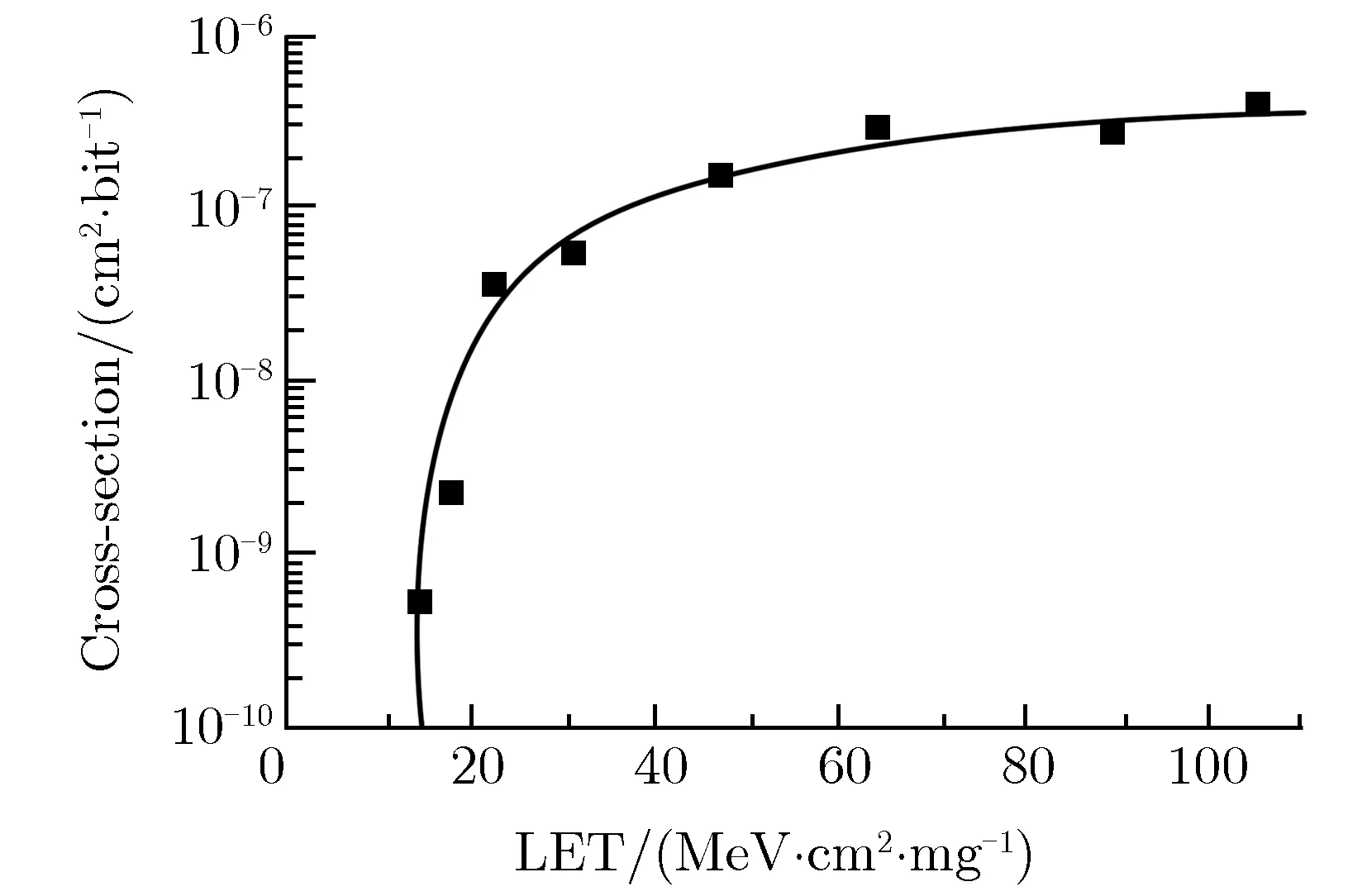
图7 单粒子软错误截面与LET值的关系曲线Fig.7 Soft error cross-section vs. LET values
3 单粒子软错误的数值仿真
抗辐射器件的设计通常遵循“设计-生产-实验”的反复循环过程,设计周期长、成本昂贵,而单粒子效应的计算机模拟能够有效降低实验成本和缩短设计周期,成为评估器件的单粒子软错误风险和抗辐射加固的重要手段。现有的研究半导体单粒子软错误的计算机仿真工具中,大多偏重半导体器件电学机制的分析,仿真速度较慢,且对于辐射环境、半导体材料、核反应等机制的分析都不够完善。而欧洲核子研究中心开发的GEANT4工具可以弥补上述仿真的一些不足。
在航天工程的设计阶段,器件的单粒子软错误评估主要依赖于地面模拟实验,但空间环境中粒子种类丰富、粒子能量可高达GeV量级,而地面模拟实验不能反映真实的空间环境,也不能分析器件内部对粒子入射的详细响应。单粒子软错误的地面模拟实验成本较高,并且我国能够用于单粒子软错误地面模拟实验的加速器有限,不能充分满足航天工程的需要。
在航天器在轨运行阶段,通过预测和监测航天器周围的辐射环境,实时监控航天器在轨器件的辐射损伤状态,可以管理和规避潜在的风险。但目前我国对航天器的在轨辐射实时监测能力不足,对卫星异常的诊断主要依靠经验推测,更不可能对潜在风险进行提前规避。随着我国在轨航天器的增多,对空间辐射效应的实时预警的需求也更加迫切。
辐射效应的计算机模拟,作为集成电路抗辐射加固研究的先进手段之一,在美国等其他国家已经得到广泛的应用。以美国为首的西方国家在20世纪70年代卫星因单粒子效应发生失效之后,便展开了抗辐射加固技术的研究。在20世纪70年代中期就着手研制开发辐射效应分析软件,目前已形成了“设计(包括理论指导下制造)-实验(包括理论研制、评估)-再设计(包括理论模拟)”的良好循环体系。特别在抗辐射加固领域,基本实现了辐射损伤机理及电子系统的工程加固设计理论与实验相结合的研究方法,可以开展半导体器件和集成电路辐射效应的计算机仿真分析与预测评估。
如图8所示,国外提出了多级层次化故障建模的概念,不仅在工艺器件级可以模拟单粒子软错误,而且在电路级也可以快速的模拟得到对应电路的抗单粒子效应能力,甚至在体系结构级都有对应的故障注入工具,可以用VHDL或Verilog实现整个系统抗单粒子能力的评估。整个流程的核心思想就是在每个层次都对故障进行抽象并应用到上一个层次。
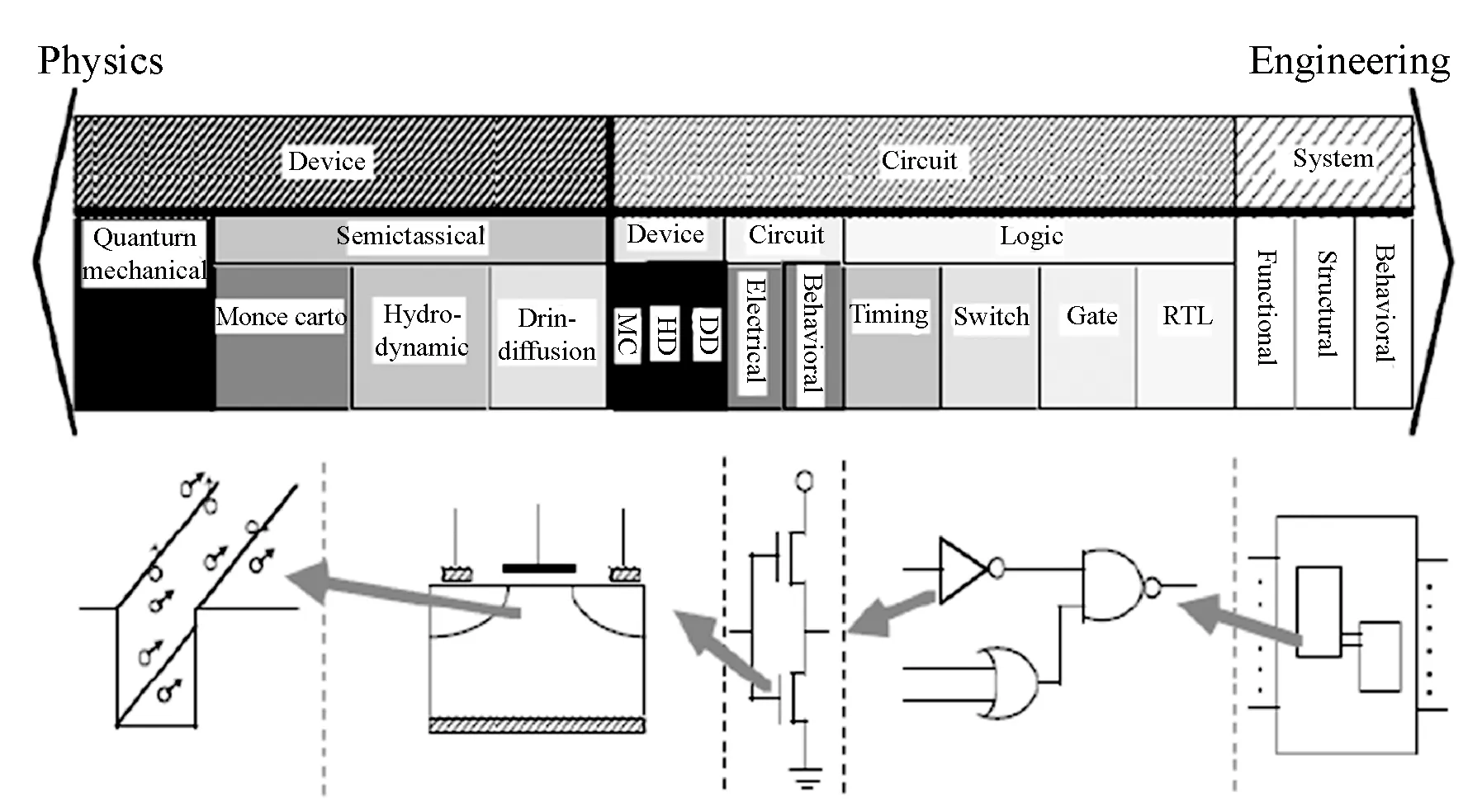
图8 多级层次化故障建模流程图Fig.8 Modeling flow of multi-level hierarchy fault
3.1 基于GEANT4的数值仿真(核物理层级)[29-30]
3.1.1 GEANT4简介
GEANT4是由欧洲核子研究中心(CERN)开发的蒙特卡罗(Monte Carlo)应用软件包,主要用于模拟高能粒子在探测器中输运的物理过程。它采用面向对象的C++语言编写, 可以构造复杂的探测器几何结构,定制感兴趣的粒子与物理过程模型,并且能够跟踪粒子的过程,显示粒子径迹,处理在输运过程中产生的大量数据。
GEANT4是一个工具包,不是一个应用程序,它没有用户界面,需要用户自己开发,编写程序代码来进行相应的应用;作为粒子物理的仿真应用,它的特点如下:
1) GEANT4用C++语言改写GEANT3的所有代码并重新加以设计,充分利用了C++语言中的优势,将程序包完全开源,便于用户和管理者共同的开发与改进,扩充和完善适合各自应用的工具包,因此GEANT4可以不断地完善,并且扩展自身的应用范围。
2) GEANT4是用面向对象的概念构建数据模型,将所有的内容统一分成各个大类和模块,使得各个模块拥有自己的独立性和特有的功能,而各个模块的接口界面便于用户的使用和管理,同时GEANT4还可以与其他工具和软件进行交互应用,利于大型的程序编写和模拟仿真。
3) 更专业系统的粒子输运物理过程,GEANT4的核心在于开发团队提供了各种不同的物理模型,它所包含的物理模型和其优化完善程度是它最大的优势所在,而且各个模型具有统一的接口方式,因此面向对象技术使物理模型的选取更加开放和透明化。用户根据粒子和能量范围,对粒子和物质相互作用的每一个物理过程,选取一个模型或几个模型,达到最优化模拟的目的。
4) 采用蒙特卡罗方法进行算法建模,通过概率统计的方法,能够更精确的描述事物的特点及物理实验过程,解决一些数值方法难以解决的问题。蒙特卡罗方法受几何条件的限制小,能够完成复杂建模,为屏蔽能谱的计算提供了便利条件;且收敛的速度与问题的维数无关,误差容易确定,程序结构简单,易于实现。
3.1.2 单粒子软错误仿真存在的问题以及引入GEANT4的意义
随着单粒子软错误的研究不断深入,不同的模型和仿真应用到了单粒子软错误的分析中,但它们仍然有很多局限的存在:
1) 空间环境中的辐射情况十分复杂。航天器在空间轨道中所处的空间环境不能十分精确地进行模拟描述,对于不同的在轨运行状态,不同空间粒子的辐射和一些特殊情况只能够做到简单的近似模拟,不能实时地将所有可能的空间环境全部考虑在内。
2) 地面实验器材的局限性。在地面建立一些粒子辐射源和发生器可以模拟空间中的一些粒子辐射,但由于地面重力作用和现有科技水平等的限制条件,对于一些较高能量和特殊的粒子辐射源还不能够生产实现,而且使用与维护这些粒子辐射源的成本也非常昂贵。
3) 现有的研究模型与计算机仿真的局限。现有的半导体器件单粒子软错误的模型还不能将入射粒子产生的直接电离与间接电离的效应很好的统一在一起模拟。尤其是大多数的研究与计算机仿真都更偏向于直接电离所产生电荷的影响,而对核反应等产生的次级粒子间接电离的影响研究仍然欠缺,缺乏很好的模型与仿真。
此外,对于半导体器件几何结构中更多细节模型的建立和仿真还不够完善,如器件的边缘效应,隔离氧和埋氧的影响等;粒子种类、能量、器件材料等对于半导体器件的单粒子软错误造成的影响不能具体的分析模拟。还有对于电荷的收集模型也不够完善,而且研究大多是关注载流子的漂移过程对电荷收集的影响,对载流子的扩散过程而产生的电荷收集模式研究不够完善,对于大型电路和系统的仿真考虑也在进一步的深入研究中。
由于以上对于半导体器件单粒子软错误研究的一些缺陷的存在,研究人员开始改变和创新一些研究方法,寻找更多的提高研究水平的途径,而在高能及空间物理中得到广泛应用的GEANT4工具逐渐进入研究者的视野。
研究半导体器件单粒子软错误的基本机制就是辐射粒子入射半导体后产生能量进而淀积生成电荷,经过半导体器件有源区对电荷的收集,最后造成对器件和电路响应的过程。而GEANT4的研究可以在半导体器件中的电荷淀积进行详细模拟,因为它在仿真半导体器件单粒子软错误上有自身的一些优势:
1) GEANT4拥有比较完善的粒子及物理模型,与TCAD、SPICE等其他常用的模拟半导体的工具相比,可以较完善地提供空间中存在的粒子和相应的辐射环境;而且它还拥有包括电磁作用,核反应过程等多种物理模型,可以比较好地对粒子与材料的作用进行模拟,这些都是其他半导体仿真工具所欠缺的。
2) GEANT4可以构造三维立体的几何结构,填充必要的半导体材料,形成的器件单位量级可以达到微米级甚至纳米级,这些都有利于对半导体的微纳尺寸下的研究,可以更精确的模拟空间辐射后半导体器件和电路中电子-空穴对的产生机制。
3) GEANT4在三维结构模拟和计算效率上都占有优势,利用蒙特卡罗的统计方法和其他优秀算法,提高了模拟的速度与可靠性,使得GEANT4能够仿真108甚至更高数量级的庞大粒子数入射情况;而且可以采集结构中的各个粒子的状态信息,尤其是粒子种类、能量、位置等对于半导体器件单粒子软错误研究比较重要的信息。
4)工具开发的灵活性;可以在GEANT4工具基础上,开发或者改善程序来特别应用到半导体辐射模拟,可以对输入输出自行处理,改善用户界面,并且与第三方工具有比较好的交互性等。
以上这些优势,促使更多的研究者开始应用GEANT4对半导体器件单粒子软错误进行深入研究,这样可以更好地反映出单粒子软错误的电荷产生机制。但同时,也必须看到GEANT4本身的一些不足和挑战,比如,它不能够模拟仿真半导体的电学特性;工具使用本身不是很方便,需要较好的大型程序编程经验以及对GEANT4程序和语法的深入理解;没有好的用户交互界面,处理与其他工具的交互困难,程序的编写、编译、链接和运行都比较繁琐。所以,要更好地应用GEANT4来研究半导体单粒子软错误,还需要更多的探索和努力。
3.2 基于TCAD的数值仿真(半导体器件层级)[31-35]
半导体工艺和器件仿真软件TCAD(technology computer aided design),采用数值仿真的方法,可以对不同的工艺条件进行模拟,也可以对不同的器件结构进行优化,从而获得理想的电学特性。主流商用的TCAD工具包括Synopsys的Sentaurus(收购了之前的ISE TCAD)、Silvaco、Crosslight、Global TCAD Solution和Cogenda等,其基本原理类似,都包含了工艺仿真和器件仿真两个主体部分。
工艺仿真首先必须建立能够模拟制造IC的各种工艺的模型,这些模型是物理或化学模型。为了用计算机对这种模型进行模拟计算,必须将这些模型用数学公式来表示。主要采用的模型包括了解析模型、经验模型、半经验模型、表格化模型和内插/外推模型。解析模型是基于理论推导,物理含义明晰,有一个精确或近似的理论表达式。经验模型是基于大量实验数据,但是机理并不清楚,采用一个经验公式来说明。半经验模型不完全基于理论推导,也不完全基于实验数据,理论表达式中某些参数的系数、指数用经验值表示。对于表格化模型,实验数据较少,应变量和自变量的关系用列表表示。内插/外推模型以较少实验数据为基础,用内插和外推法补充已知实验数据点之间的数据,外推已知实验数据区外的数据。工艺仿真以工艺参数和衬底参数为输入,输出包括各种杂质分布、各层的厚度和形貌和方阻等。工艺参数,以离子注入为例,包括了注入能量、注入剂量和杂质类型等;以扩散工艺为例,包括温度、时间、杂质类型、气氛及分压等;以氧化工艺为例,包括了温度、时间、干氧还是湿氧以及分压等。衬底参数指采用什么材料的衬底,如体硅、SOI和化合物半导体等,衬底的晶向、掺杂类型和浓度等。
器件仿真以杂质分布、几何参数、位置参数和网格参数等为输入,求解对象为载流子(电子和空穴),输出结果包括了外部的端特性(电压和电流等)和内部的场特性(电场和电势等)。杂质分布的输入可以对应工艺模拟软件的输出或者用一个描述杂质分布的解析表达式;几何参数例如MOS型器件的沟道长度、沟道宽度和栅氧化层厚度等;位置参数例如为界面和区域等;网格参数指网格化的设置与优化。器件仿真的基础是漂移扩散模型(drift-diffusion model),以电势、电子浓度和空穴浓度为自变量,耦合求解Poisson方程和电子/空穴连续性方程。广泛用于半导体载流子输运仿真,但不能描述速度过冲,并且过高的估计了碰撞电离产生率。热力学模型(thermaldynamic model)是在漂移扩散模型的基础上,添加电致热效应。耦合求解Poisson 方程、载流子连续性方程以及晶格(载流子温度方程)。载流子假定与晶格是热平衡的,故此模型可以用来模拟晶格自加热效应。在模拟高电流时需要加入热力学模型,例如模拟功率器件、高栅或漏偏置的MOSFETs以及开路的双极晶体管等,大电流产生的焦耳热会明显提高晶格温度,而模拟中所采用的产生/复合模型、载流子迁移率模型以及雪崩倍增模型均是晶格温度的函数,因此需要求解热流方程来提高模拟的准确度。流体力学模型(hydrodynamic model)是在漂移扩散模型的基础上,分开添加载流子温度和晶格温度的计算项,考虑它们之间的热交换。耦合求解Poisson 方程、载流子连续性方程以及能量平衡方程,适合模拟特征尺寸在0.18 μm以下的深亚微米器件、异质结器件以及部分耗尽的带浮体效应的SOI器件模拟,在模拟击穿特性时,在该模型可有效的避免漂移-扩散模型中因局域电场假设而引起的过早击穿。
无论是工艺仿真还是器件仿真,都需要将模拟的定义区域分割成小的子区域,每个小的子区域常称作网格。网格间距应足够小,最终保证因变物理参数的分布有足够的精度。另一方面,网格间距也不能过小,白白浪费计算资源(存储空间和计算时间)。网格划分的方式决定了采用哪一种数值方法。同时,网格划分的好坏,也直接影响到数值解是否收敛及收敛速度的快慢。在半导体器件数值模拟中,模拟的可靠性和精确度强烈地依赖于网格的划分。很明显,网格划分得越密,得到的结果精度就越高,可是计算量会随着网格点数的平方而加大。
将所选模型方程在一定的网格系统内进行离散,这种离散是根据一定的数学知识和物理知识得来的,那么网格节点处的所求变量值就可以用来近似地描述这些微分方程中各物理量之间的数学关系。然后再结合边界条件,求解离散得来的方程组,就可以得到各网格节点处的所求变量值的变化量,用这一离散的变量分布式近似代替原微分方程的解析解。对于离散后的方程组,如果没有边界条件,方程组的解有无穷多个,而实际物理问题一般有确定的解,特别是在数值仿真方面,都有确定的数值解。任何物理研究都是在一定的条件下进行的,都存在于特定的时空中,所以边界条件体现了物理问题中所研究的实体与周围环境之间的关系,确定的边界条件使得物理问题的环境确定下来。半导体器件边界条件包括物理边界,如欧姆接触界面、肖特基接触界面和半导体/介质接触界面等;还包括了人为边界。“人为边界”是人为划定的,如晶体管的外表面或衬底接触面。由于在人为边界上,电位和载流子浓度都是未知的,这种条件可以使用Neumann边界条件。
当对半导体基本物理模型离散后,得到的是一系列非线性的方程组,通常称为偏微分方程组。半导体数值方法的最后一步就是求解这个高达数千阶的偏微分方程组。偏微分方程组的解法有非耦合法(Gummel)和耦合法(Newton)两种。每一种求解方法都需要一个试探性的初始解,然后根据一定的标准,不断调整解直至收敛。非耦合法是在方程之间弱耦合的假设情况下才成立的。如果得到的一系列偏微分方程组之间的耦合性很强烈,比如器件工作于大电流、高电压的工作条件下,非耦合法收敛很慢,甚至失效。在这类问题的模拟中,应该采用耦合法。假设有N个离散点,一般情况下,非耦合法只需要求解3个(N×N)阶的稀疏矩阵,然而耦合法则需要求解一个3N×3N阶的系数矩阵,所以耦合法要比非耦合法占用更多的储存单元,且计算量大。耦合法的缺点是需要构造和存储复杂的Jacobi矩阵,每次迭代需要解庞大的线性方程组,直接求解法需要大量的内存。幸运的是,随着计算机内存和性能的提高,解大规模线性方程组所需要的内存和时间变得可以接受,因此耦合法得到了广泛的应用。对于任何一种方法,都必须求解矩阵。这些矩阵相当大,它们的阶数通常在100和400之间。一般情况下,它们都是稀疏的,因为每一行的非零元素个数少于总数的5%。
以Synopsys的Sentaurus TCAD为例,介绍其单粒子软错误仿真采用的物理模型。单粒子软错误是器件逻辑状态的偶然性转变,在双极和 MOS 技术中都可以观察到这种现象。当重粒子穿透器件结构,损失能量,产生大量电子-空穴对,引起电流突变,从而改变器件的逻辑状态(如存储单元中的 0 和 1)。影响单粒子效应的重要因素包括:入射粒子的能量和类型,入射粒子的角度, LET 值与产生电子-空穴对数目间的关系。单粒子入射过程如图 9所示。

图9 重粒子入射到半导体材料中示意图Fig.9 Illustration of heavy ion striking semiconductor material
重粒子引起的电子-空穴对产生率如下:
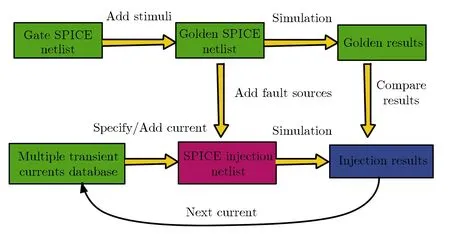
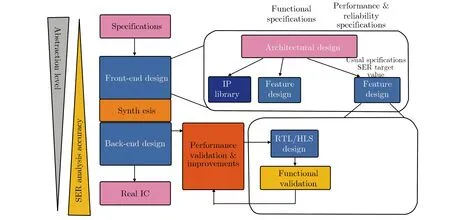
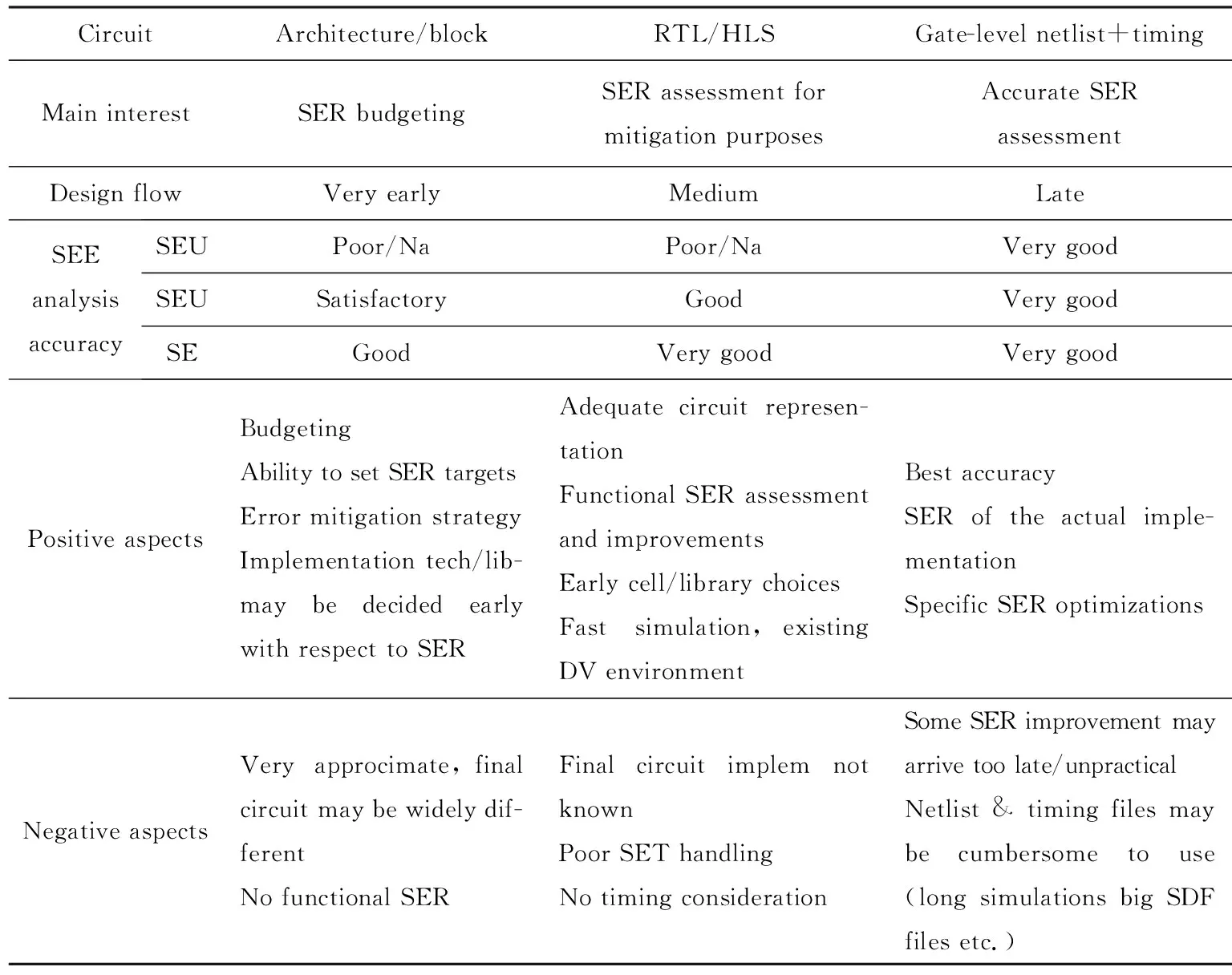
当l G(l,w,t)=GLET(l)×R(w,l)×T(t) 当l≥lmax, G(l,w,t)=0 式中,R(w,l)和T(t)分别描述产生速率随空间位置和时间的变化;GLET(l) 是线性能量转移产生密度,单位为cm-3。 T(t)定义为高斯函数: 式中,theavyion是重离子入射的时间;Shi是高斯函数的特征值。 空间分布函数R(w,l)默认定义为指数函数: 也可以定义为高斯函数: 式中,w是据离化路径的垂直距离;wt为特征距离,是离化路径l的函数。 线性能量转移产生密度GLET(l)如下: GLET(l) =a1+a2×l+a3ea4×l+ k'[c1×(c2+c3×l)c4+LET_f(l)] 式中,LET_f(l)是离化路径l的函数,cm-3,当激活关键词PicoCoulomb时,单位变为pC·μm-1。 SPICE(simulation program with integrated circuit emphasis)是最为普遍的电路级模拟程序,SPICE的网表格式成为了通常模拟电路和晶体管级电路描述的标准。SPICE仿真软件模型与仿真器紧密地集成在一起,SPICE模型由两部分组成:模型方程式和模型参数。由于提供了模型方程式,因而可以把SPICE模型与仿真器的算法非常紧密地联接起来,可以获得更好的分析效率和分析结果。SPICE模型已经广泛应用于电子设计中,可对电路进行非线性直流分析、非线性瞬态分析和线性交流分析。被分析的电路中的元件可包括电阻、电容、电感、互感、独立电压源、独立电流源、各种线性受控源、传输线以及有源半导体器件。SPICE内建半导体器件模型,用户只需选定模型级别并给出合适的参数。理想的元器件模型,应该既能正确反映元器件的电学特性又适于在计算机上进行数值求解。一般来讲,器件模型的精度越高,模型本身也就越复杂,所要求的模型参数个数也越多。这样计算时所占内存量增大,计算时间增加。而集成电路往往包含数量巨大的元器件,器件模型复杂度的少许增加就会使计算时间成倍延长。反之,如果模型过于粗糙,会导致分析结果不可靠。因此所用元器件模型的复杂程度要根据实际需要而定。如果需要进行元器件的物理模型研究或进行单管设计,一般采用精度和复杂程度较高的模型,甚至采用以求解半导体器件基本方程为手段的器件模拟方法。二维准静态数值模拟是这种方法的代表,通过求解泊松方程,电流连续性方程等基本方程结合精确的边界条件和几何、工艺参数,相当准确的给出器件电学特性。而对于一般的电路分析,应尽可能采用能满足一定精度要求的简约模型,如BSIM模型。 等效电流源模型,如图10所示,在单管的基础上加了两个电流源IDC、ISC和两个电容CBS、CBD。IDc、ISc分别代表漏到体和源到体的传导电流,IDd、ISd分别代表漏到体和源到体的电流。由于漏端正电压会产生大的电场使得电子向漏端运动,因此一般情况下,IDc比ISc要大一点。图10为在电路模拟软件Power Spice中使用的等效电路。 其中,It是瞬时注入电流;XQ是注入的总电荷。τr和τf可以通过与 3D Fielday模拟拟合获得。利用图11在Power Spice中模拟可以得到临界电荷。注入脉冲电流的电荷的总和(由XQ定义)叫做电路的临界电荷。具有最小临界电荷的晶体管的临界电荷是电路存储单元的临界电荷。 图10 晶体管等效电路 (电流源表示粒子入射)Fig.10 Transistor equivalent circuit (current sources represent particle injection) (a) (b) (c) 图11PowerSpice中使用的电荷注入方法 针对每个门电路构建电流脉冲库,并在SPICE仿真中进行注入,从而确定门电路输出端电压脉冲的宽度与发生概率。仿真方法如图12所示。进行分析时,必须考虑:(1)单元SPICE网表;(2)敏感区列表或者注入列表;(3)瞬态脉冲优化库。考虑到电路版图的特征,确定不同的敏感区,生成包含数千个瞬态脉冲的库。针对特定的设计,瞬态电流的形貌、宽度和幅值的差别非常大。为了进行快速评估,必须精简用于注入的电流脉冲数量。通过仔细分析电流的参数和特征(形貌、幅值和宽度),可以对电流进行分类,从而获得精简的电流库。自动多电流注入模块修改初始的SPICE电路网表,在识别的敏感区自动添加电流源。为了更贴近真实情况并进行简化,可以采用SPICE分段线性波形(PWL)电流格式表征注入的电流。采用PWL文件进行电流注入仿真,可以自动化处理,使得故障注入仿真更容易,也会提高计算的精度。 图12 多瞬态电流仿真Fig.12 Multiple transient currents simulation 分析和精简多瞬态电流非常重要,特别当生成的瞬态电流列表非常大时。精简用于仿真的瞬态电流数量,可以大幅度地减少仿真时间。在进行瞬态电流分类时,必须考虑到单个入射事件引起的多个电流脉冲,并采用n元组电流脉冲来处理。对n元组电流创建类之前,首先要分类每个电流脉冲。第一次分类是基于瞬态电流的形貌。首先,定义电流形貌的类型;然后,针对每个类型用不同的特征进行描述,包括幅值、斜率和30%幅值处的宽度等。采用这些判据,可以区分每一类中的脉冲类型。 这一步可以快速和弹性地定制化等效类。每一类的瞬态电流都可以用一个瞬态电流来代表。因此可以大幅度地减少仿真的瞬态电流数量。折中考虑到仿真的时间和精度,针对每一类,选择上述的三个参数用于等效判据,从而可以确定等效类的数量。如果用户选择大量的类,每个类的参数都比较接近,则精度会提高,但仿真时间会增加。反之,如果选择的类很少,每个类的参数相差较大,则仿真时间会减少,但精度会降低。完成对电流的分类之后,还需要进一步分类电流n元组。有属于同一类组分的n元组将会被归类到一起。例如NAND2门电路有3敏感区。初始产生了88 755个 电流。定义了3种电流形貌,针对每种形貌创建16个电流类。最后,使用这些电流类构建n元组。经过这一过程,电流数量减小至3 399,占最初数量的3.83%。 在已识出来的敏感区进行多瞬态电流故障注入。如图13所示,如果区域1、2和3相连,一定能量的中子入射,不管偏置条件如何,都会同时向这三个敏感区注入瞬态电流。如果是重离子入射,仅认为标示的漏区为敏感结点。所以必须确定不同输入矢量下的标示漏区,针对特定的输入组合,仅对标示的漏区进行瞬态故障注入。首先仿真所有输入组合下的电路特性,考虑每个晶体管的栅压值,从而确定其漏端是否需要被标示。这样,针对每一种输入组合,都创建了标示漏区的列表。 (a) Layout (b) Corresonding schematic 表2给出了NAND2门电路的标示漏区,用于重离子敏感度分析。同时还要确定标示漏区对应的晶体管类型(NMOS还是PMOS),从而确定注入电流的符号。 表2 NAND2门电路的敏感区标示Tab.2 Labeled sensitive regions in NAND2 gate circuit 采用自动化仿真,可以在一个仿真进程中,考虑复杂逻辑门电路所有可能的输入组合,并对数千个n元组电流进行模拟。仿真的算法如下所示: for each analyzed design add stimuli and fault sources in the netlist for eachn-tuple of currents for each input combination multiple injection in sensitive zones save outputs 图14给出了自动化仿真流程。在有效仿真之前,需要进行不同阶段的网表处理。首先执行标准仿真,仅添加输入激励。然后,添加电流源。对于每个n元组电流仿真,产生新的网表,用真实的故障源替换掉之前的故障源模板。 每次故障注入时,电路单元输出端的电压脉冲以PWL格式保存,从而可以较容易地对比标准结果和故障注入仿真结果。在比较阶段,电路单元输出端的电压脉冲宽度在VDD/2幅值处进行取值,如图15所示。实际上,对于每个输入组合与故障注入仿真,都要计算瞬态脉冲的宽度。 图14 自动仿真方法Fig.14 Automatic simulation technique 图15 瞬态故障宽度测量Fig.15 Transient fault width measurement 评估软错误情况下电路的行为特性。软错误仿真借鉴了很多DFT(可测性设计)领域的成果。在电子设计实践中,大量研究和使用故障仿真技术。最大的挑战之一是处理的故障数量庞大。特定是,SET可以在任何时刻发生和到达,脉冲宽度PW有较大的范围。故障仿真的方法对于软错误仿真也是有用的: 首先,背景是特定的。根据电路设计文件、验证环境和仿真工具,定义电路表征和故障模型,如之前所讨论的。其次,构建故障集,枚举仿真中需要考虑的故障。电路描述用来确定电路特征,以便采用正确的故障模型。门级网表中包含组合单元和时序单元,组合单元输出采用SET模型,而时序单元采用SEU模型。RTL表征产生信号列表,随后被综合成触发器,可以采用SEU模型。大规模电路中会有大量的故障,因此需要精简仿真所需的故障数。再次,仿真故障集中的故障,通常采用一些技术来加速仿真。还会采用一些其他的技术,确定仿真的故障是否产生真正的失效,并且记录相应的错误数据。仿真的一个重要方面是,根据其对电路功能的影响进行故障分类。最后,分析仿真数据,提供给用户故障注入后电路行为的相关数据。此外,进一步处理故障数据,基于已有的数据进行外推,形成完整的分析报告。 如图16所示, 软错误率分析被包含进典型的设计流程中, 而软错误率要求则作为电路整体可靠性的一部分。 图16 设计流程中的软错误率分析Fig.16 Soft error rate analysis in design flow CircuitArchitecture/blockRTL/HLSGate-level netlist+timingMain interestSER budgetingSER assessment formitigation purposesAccurate SERassessmentDesign flowVery earlyMediumLateSEEanalysisaccuracySEUPoor/NaPoor/NaVery goodSEUSatisfactoryGoodVery goodSEGoodVery goodVery goodPositive aspectsBudgetingAbility to set SER targetsError mitigation strategyImplementation tech/lib-may be decided early with respect to SERAdequate circuit represen-tationFunctional SER assessment and improvementsEarly cell/library choicesFast simulation,existing DV environmentBest accuracySER of the actual imple-mentationSpecific SER optimizationsNegative aspectsVery approcimate,final circuit may be widely dif-ferentNo functional SERFinal circuit implem not knownPoor SET handlingNo timing considerationSome SER improvement may arrive too late/unpracticalNetlist & timing files may be cumbersome to use (long simulations big SDF files etc.) 单粒子效应是电路系统整体可靠性的一部分。确实,SEE可以导致功能暂时或永久性丧失,以及数据破损。可靠性工程师可以采用经典的可靠性概念,用来建模和汇总SEE对电路行为的影响。执行该计算,SEE分析可以分成若干步骤,呼应标准设计流程中的概念。更为重要的是,专业人员可以在SER(软错误率)分析流程中分享和交换SER知识与技能,处理不同的步骤。 第一步要考虑每个单元的物理现象与行为。该分析耗时耗力,需要测试电路设计、辐照实验以及特定的工具等。然而,对于特定的单元库,该过程仅需一次。第一步的结果是,特定环境下,组合单元、时序单元和存储单元的SET/SEU发生概率。出于完整性的考虑,需要给出瞬态脉冲的宽度分布。由于受影响单元输出端的瞬态脉冲幅值过小或宽度过窄,有一些SET对电路没有任何影响。因此引入电学降额EDR的概念,用来描述这类SET的百分比。SER表征结果与标准单元库相关。设计工程师使用该结果评估电路的敏感度,并进一步优化。 第二步考虑从受影响单元的输出端沿电路路径的故障传输。需要注意的是,SEE会在时钟周期的任何时刻发生。SEE发生时刻相对于时钟边沿的位置,决定了该故障能否在锁存窗口内到达一些时序单元,并转化为错误。可以引入时序降额的概念,考虑上述效应。从逻辑角度,故障能否传输,可以引入逻辑降额的概念。该步骤决定了,初始SEU/SET沿组合逻辑传输,被流水线中时序单元捕获,并产生软错误的概率。因此该步骤决定了,在SEU/SET发生的时钟周期内它们的影响。然后进一步分析在后续的时钟周期内,软错误在整个电路设计中传输所产生的影响。 第三步处理更高阶的软错误结果。这些错误有可能被丢弃,对电路没有任何影响;有可能潜伏在电路中,在一定时长内,没有观测到失效;也有可能导致不同严重性程度的失效。可以引入功能性降额的概念,来表征能够引起失效的错误的比例。 需要强调“初始时钟周期”降额(包括电学/时序/逻辑降额)和“多时钟周期”降额(功能性降额)间的差异。在初始时钟周期,故障的传输和锁存与工艺、标准单元库以及电路网表实现强相关。初始时,在RTL/HLS/更高阶表征相同的情况下,电路的具体实现可以有多种选择,并且在出现故障时它们的行为特性不同。然而,只要RTL描述相同,即使电路的具体实现不同,功能性降额都是一样的。因此,对于电学、时序和逻辑降额,需要电路表征与最终实现相匹配。而对于功能性降额,可以采用更高阶的描述。 可以在门级对SET进行建模,即特定时长内逻辑值取反。选择该时长有一定技巧,要求故障仿真和更精确的仿真方法(例如模拟法)对电路产生的影响相同。有时,这无法实现。因为门级电路和信号传输模型不够准确,不适合仿真小幅值和窄宽度的瞬态脉冲。可以采用模拟SPICE仿真,更为准确地评估SET沿组合单元网络传输,直至确定SET消失,或者信号足够强,仅用逻辑仿真就能够充分评估。对于电学降额,需要评估有效逻辑脉冲,其对电路的影响与初始模拟脉冲相同。具体评估的方面有受影响单元输出端的容性负载,SET斜率与下游单元的线性行为和SET幅值与下游单元的阈值电压。 当时序单元结点的电流脉冲足够强时,单元状态翻转,产生SEU,单元输出改变,直到时钟周期末新值被锁存。与之相反,SET在组合逻辑单元输出端产生短脉冲,并且可能在时钟周期结束前消失。SET从生成位置开始,沿组合逻辑单元传输,直到时序单元输入端(通常是触发器)。如果瞬态故障被时序单元捕获,则产生错误;否则将消失,没有任何影响。为了被捕获,故障必须在锁存窗口内到达时序单元输入端。触发器的锁存窗口对应于tsetup和thold。该时长内的故障是发生时刻和传输路径延迟的函数,也依赖于到达触发器输入端瞬态脉冲的宽度和波形。到达触发器输入端瞬态脉冲的宽度和波形,依赖于初始瞬态波形的宽度与波形,以及沿电路单元传输引起的变形。 逻辑降额(LDR)用来评估逻辑故障从受影响单元输出传输到时序/存储单元输入的过程。根据电路的状态(信号值和单元输出值),故障传输可能会受到逻辑屏蔽。例如,对于AND门电路,单个低电平的输入会屏蔽所有其他输入端的故障。可靠性领域对于LDR评估已经研究得较为透彻。设计者可以参考很多研究论文、方法和工具,来评估电路LDR。对于非常复杂的电路和设计,可以采用标准的仿真器(编译器驱动、表格驱动或者事件驱动)进行故障注入和仿真。为了优化故障传输评估,可以采用一些特定的仿真技术,例如并行故障仿真、单图形并行故障传输和并行图形单故障传输等。 功能降额(FDR)的目的在于评估SE是否对电路/板级/系统的功能造成可观测到的影响。功能降额考虑到了电路的真实使用情况,以及系统的功能。通常,熟识系统架构和功能的人员给出是否失效的判据。因此,功能降额的评估工作,需要可靠性工程师(软错误率专家)和系统工程师协同工作。此外,临界参数可以添加至故障类,所以失效分类有一些主观性。而且,电路的工作情况对失效分析有显著的影响。不同模式和应用的电路,其软错误相关的失效也不同。所以,功能降额评估必须考虑特定的功能,以及相关功能参数的影响。对于CPU等通用电路,其应用范围非常广,使得FDR分析非常复杂。FDR计算需要考虑多个时钟周期内的软错误传输。这是为了评估a) 软错误是否消除,是否已对电路工作没有了影响;b) 是否潜伏在电路里,不能观测其对电路工作的影响;c) 是否产生功能性失效。 上文提出了SEE仿真的工具和方法,该方法可以精确表征辐照环境下电路的行为特性。但是分析时间过长,需要在规划项目进度时将其考虑进去。此外,可靠性工程师和设计工程师的协同也非常重要,因此限制了软错误专家的自主性。任何软错误率相关的优化,都需要反馈给设计工程师,因此需要更多的时间。 设计工程师经常需要可靠和快速的工具,进行快速设计迭代和电路优化。执行软错误率评估等分析,情况也是相同的,需要专业的知识与技能。多数情况,软错误率工具会集成到标准的设计流程中(例如,快速原型平台),采用标准的文件格式和概念。此外,在设计流程中,不同的工程师要共享软错误率数据(例如,单元软错误率表征数据)。 SER工具可以提供静态方法,快速评估电路或系统的软错误率,满足上述需求。这种情况下,降额因子非常有用,因为全局SER是不同电路部分SER与不同的降额因子相乘再求和。该方法非常灵活,可以在不同的表征层级上对电路进行划分。基于门级网表,已知电路的具体实施和详细数据,可以计算每个单元对于软错误率的贡献。基于模块级,可以快速评估整个系统的软错误率,然后构建充分的错误处理方法和软错误率约束,为实施团队提出意见。 长期以来,缩小集成电路芯片的特征尺寸和增大硅片直径是推动集成电路技术进步的两大要素。近年来,随着传统工艺和常规材料物理极限的逼近以及研发成本的急剧上升,这一路线越来越难以实现摩尔定律的持续。在此形势下,摩尔定律开始出现新的驱动方式,主要有三个方向:1) 延续摩尔定律;2) 超越摩尔定律;3)跨越硅基CMOS。 1) 延续摩尔定律 面向高性能、低功耗、低成本的集成电路市场需求,通过新工艺、新材料和新结构器件的创新和引入,推动集成电路芯片的特征尺寸继续向不断缩小的方向发展。 该方向相关的主要技术包括: 新工艺:如7纳米及以下逻辑工艺、1x纳米及以下存储器制造工艺等; 新材料:如高k栅介质/金属栅材料、Ge/III-V族高迁移率沟道材料、GeSi源漏应变材料等; 新结构:如三维多栅逻辑器件(FinFET)、隧穿型逻辑晶体管(TFET)、纳米线、三维存储器(3D)、阻变存储器(RRAM)、自旋转移力矩磁存储器(STT-MRAM)等。 2) 超越摩尔定律 面向物联网、移动互联网、智能机器人等新兴信息产业的市场需求,以价值优先和功能多样化为目标,不特别强调缩小芯片特征尺寸,通过新型器件和电路的功能扩展及多功能集成,向以非缩比驱动的新功能器件开发与系统集成方向发展,为集成系统在数字化“大脑”周围建立起感知和连接外部世界的能力。 该方向相关的主要技术包括: 新功能器件:如模拟芯片、射频芯片、生物芯片、功率器件、能源器件、光电子器件、MEMS传感器等; 集成技术:如系统级封装(SiP)、三维芯片集成(3D IC)、多功能系统级组装等。 3) 跨越硅基CMOS 随着集成电路特征尺寸的进一步缩小,单纯靠器件微缩来提高器件性能和集成度的技术路线已经受到基本物理原理和高功耗的限制。而随着物联网、互联网+、大数据的蓬勃发展,人类对于高速、低功耗、高密度信息处理和存储技术的要求却越来越高,以新材料、新结构和新原理为特点的后摩尔时代信息器件技术开始得到学术界和工业界的广泛关注,成为微纳制造电子科学的重大前沿,也是未来各国竞相力争的重大高技术领域。 目前,美国、日本、欧盟、韩国等集成电路产业强国以及英特尔、台积电、三星等集成电路工业巨头都投入了大量人力和物力开发后摩尔时代的新器件技术。该方向相关的主要技术包括: 基于电荷传输的新型器件:如负电容器件、原子开关器件、基于新材料(如石墨烯、碳纳米管、有机材料、MoS2、WSe2)的器件等; 基于非电荷传输的新器件:如自旋器件、量子器件、光子器件、极化器件、等离子器件、纳米磁畴器件、分子态和声子器件等。 虽然按照摩尔定律的等比例缩小步伐大幅度变缓,但大量的新材料、新工艺、新器件、新电路和新应用不断涌现,而关于它们的单粒子软错误的数值仿真和实验技术还几乎处于空白状态,太多的研究工作等待着学者们开展和挖掘。 此外,进入到了纳米尺度,工艺的波动性对器件和电路的影响越来越严重。几乎没有制造工艺会不受其制造实体变化的影响,这对于半导体产业尤为如此,因为某些关键层仅有几个原子厚度。半导体器件的行为和特征受变化的制造参数影响严重。厂商们已经对量产产品的波动性进行了多年的整合。在产品波动性的预定窗口内,可以保证晶体管的功能和性能。另一方面,很少有关于这方面软错误研究被发表,而沟道中的随机掺杂波动(RDF)可能严重影响阈值电压,从而改变器件对辐射的响应。这需要在纳米尺度下单粒子软错误的数值仿真中予以考虑。 [1]陈伟, 杨海亮, 郭晓强, 等. 空间辐射物理及应用研究现状与挑战[J]. 科学通报, 2017, 62(10): 978-989. (CHEN Wei, YANG Hai-liang, GUO Xiao-qiang, et al. The research status and challenge of space radiation physics and application[J]. Chin Sci Bull, 2017, 62(10): 978-989. [2]陈伟, 丁李利, 郭晓强. 半导体器件辐射效应数值模拟技术研究现状与发展趋势[J]. 现代应用物理, 2018, 9(1): 010101. (CHEN Wei, DING Li-li, GUO Xiao-qiang. Current research and development tendencies of modeling and simulation of radiation effects in semiconductor devices[J]. Modern Applied Physics, 2018, 9(1): 010101. [3]陈伟, 郭晓强, 姚志斌, 等. 空间辐射效应地面模拟等效的关键基础问题[J]. 现代应用物理, 2017, 8(2): 020101. (CHEN Wei, GUO Xiao-qiang, YAO Zhi-bin, et al. Key basic issues in equivalent gound simulation of space radiation effects[J]. Modern Applied Physics, 2017, 8(2): 020101.) [4]刘忠立. 先进半导体材料及器件的辐射效应[M]. 北京: 国防工业出版社, 2008. (LIU Zhong-li. Radiation Effects in Advanced Semiconductor Materials and Devices[M]. Beijing: National Defense Industry Press, 2008.) [5]刘文平. 硅半导体器件辐射效应及加固技术[M]. 北京: 科学出版社, 2013. (LIU Wen-ping. Radiation Effects and Hardening Techniques of Silicon Semiconductor Devices [M]. Beijing: Science Press, 2013.) [6]BAGATIN M, GERARDIN S. Ionizing Radiation Effects in Electronics: From Memories to Imagers[M]. CRC Press, 2015. [7]WEIDE-ZAAGE K, CHRZANOWSKA-JESKE M. Semiconductor Devices in Harsh Conditions[M]. CRC Press, 2016. [8]SCHRIMPF R D, FLEETWOOD D M. Radiation Effects and Soft Errors inn Integrated Circuits and Electronic Devices [M]. World Scientific, 2004. [9] CRESSLER J, MANTOOTH H. Extreme Environment Electronics [M]. CRC Press, 2012. [10] BI J S, HAN Z S, ZHANG E X, et al. The impact of X-ray and proton irradiation on HfO2/Hf-based bipolar resistive memories [J]. IEEE Trans Nucl Sci, 2013, 60(6): 4 540-4 546. [11] 韩郑生. 抗辐射集成电路概论[M]. 北京:清华大学出版社,2011. (HAN Zheng-sheng. Introduction to Radiation Hardened Integrated Circuit[M]. Beijing: Tsinghua University Press, 2011.) [12] 赖祖武. 抗辐射电子学:辐射效应及加固原理[M]. 北京:国防工业出版社,1998. (LAI Zu-wu. Radiation Hardened Electronics: Radiation Effect and Hardening Principles[M]. Beijing: National Defense Industry Press, 1998.) [13] 沈自才. 抗辐射设计与辐射效应[M]. 北京:中国科学技术出版社,2015. (SHEN Zi-cai. Radiation Hard Design and Radiation Effects[M]. Beijing: China Science and Technology Press, 2015.) [14] 沈自才. 空间辐射环境工程[M]. 北京:中国宇航出版社,2013. (SHEN Zi-cai. Space Radiation Environment Engineering [M]. Beijing: China Space Press, 2013.) [15] IBE E. Terrestrial Radiation Effects in ULSI Devices and Electronic Systems[M]. Wiley-IEEE Press, 2015. [16] 韩郑生,毕津顺. 现代电子系统软错误[M]. 北京:电子工业出版社,2016. (HAN Zheng-sheng, BI Jin-shun. Soft Errors in Modern Electronic Systems [M]. Beijing: Publishing House of Electronics Industry, 2016.) [17] 韩郑生,沈自才,丁义刚,等. 空间单粒子效应[M]. 北京:电子工业出版社, 2016. (HAN Zheng-sheng, SHEN Zi-cai, DING Yi-gang, et al. Single Event Effects in Aerospace [M]. Beijing: Publishing House of Electronics Industry, 2016.) [18] 王跃科, 邢克飞, 杨俊, 等. 空间电子仪器单粒子效应防护技术[M]. 北京:国防工业出版社, 2010. (WANG Yue-ke, XING Ke-fei, YANG Jun, et al. Single-Event-Effects Mitigation Techniques for Space Electronics Equipment [M]. Beijing: National Defense Industry Press, 2010.) [19] 陈伟, 石绍柱, 宋朝晖, 等. 大气中子在先进存储器件中引起的软错误[M]. 北京: 国防工业出版社, 2015. (CHEN Wei, SHI Shao-zhu, SONG Chao-Hui, et al. Terrestrial Neutron-Induced Soft Errors in Advanced Memory Devices [M]. Beijing: National Defense Industry Press, 2015.) [20] SAYIL S. Soft Error Mechanisms: Modeling and Mitigation[M]. Springer, 2016. [21] AUTRAN J, MUTEANU D. Soft Errors: From Particles to Circuits [M]. CRC Press, 2015. [22] REN Y, CHEN L, BI J S. An RHBD bandgap reference utilizing single event transient isolation technique [J]. IEEE Trans Nucl Sci, 2016, 63(3): 1 927-1 933. [23] WANG H B, LIU R, CHEN L, et al. A novel built-in current sensor for N-WELL SET detection [J]. Journal of Electronic Testing Theory & Appliacations, 2015, 31(4): 395-401. [24] 吴驰, 毕津顺, 滕瑞, 等. 复杂数字电路中的单粒子效应建模综述[J]. 微电子学,2016,46(1): 117-123. (WU Chi, BI Jin-shun, TENG Rui, et al. Review of modeling for single event effect in complex digital circuits [J]. Microelectronics, 2016, 46(1): 117-123.) [25] BI J S, HAN Z S. Mitigation of soft errors in resistive switching random-access-memories [C]// IEEE International Conference on Electron Devices and Solid-State Circuits, Chengdu, 2014. [26] 郭红霞,陈雨生,周辉,等. 静态随机存储器单粒子翻转效应的二维数值模拟[J]. 原子能科学技术, 2003, 37(6): 508-512. (GUO Hong-xia, CHEN Yu-sheng, ZHOU Hui, et al. Two-dimensional numerical simulation of the effect of single event upset for SRAM [J]. Atomic Energy Science and Technology, 2003,37(6): 508-512.) [27] 毕津顺. 部分耗尽SOI器件研究[D]. 北京:中国科学院,2008. (BI Jin-shun. Study on partially depleted SOI devices [D]. Beijing: Chinese Academy of Sciences, 2008.) [28] GU S, LIU J, ZHAO F, et al. Influence of edge effects on single event upset susceptibility of SOI SRAM [J]. Nucl Instru Methods Phys B, 2015, 342: 286-291. [29] 贾少旭. 基于GEANT4的半导体器件单粒子翻转效应研究[D]. 北京:中国科学院, 2013. (JIA Shao-xu. Study on single-event-upset effects in semiconductor devices by GEANT4[D]. Beijing: Chinese Academy of Sciences, 2013.) [30] 贾少旭, 毕津顺, 曾传滨, 等. 核反应影响半导体器件单粒子翻转的GEANT4仿真[J]. 核技术, 2012, 35(10): 765-770. (JIA Shao-xu, BI Jin-shun, ZENG Chuan-bin, et al. Geant4 simulation of contribution of nuclear reaction to single event upset [J]. Nuclear Technique, 2012,35(10): 765-770.) [31] BI J S, ZENG C B, GAI L C, et al. Estimation of pulsed laser induced single event transient in a partially-depleted silicon-on-insulator 0.18 μm MOSFET [J]. Chinese Physics B, 2014, 23(8): 631-635. [32] BI J S, CHEN L, HAN Z S, et al. Body bias effects on the single-event-transient response of PDSOI devices [C]// IEEE Radiation and its Effects on Components and Systems, Moscow, 2015. [33] 郭红霞,张义门,陈雨生,等. MOSFET单粒子翻转效应的二维数值模拟[J]. 西安电子科技大学学报,2002,29(4): 461-464. (GUO Hong-xia, ZHANG Yi-men, CHEN Yu-sheng, et al. Two-dimensional numerical simulation of the effect of the single event upset for MOSFET [J]. Journal of Xidian University, 2002,29(4): 461-464.) [34] 李培,郭红霞,郭旗,等. 锗硅异质结双极晶体管单粒子效应加固设计与仿真[J]. 物理学报,2015,64(11): 118502. (LI Pei, GUO Hong-xia, GUO Qi. Simulation and sesign of single event effect radiation hardening for SiGe hetero junction bip olar transistor[J]. Acta Phys Sin, 2015,64(11): 118502.) [35] 毕津顺, 海潮和, 韩郑生. 深亚微米SOI射频 LDMOS功率特性研究 [J]. 物理学报, 2011, 60(1): 081501. (BI Jin-shun, HAI Chao-he, HAN Zheng-sheng. Study on power characteristics of deep sub-micron SOI RF LDMOS [J]. Acta Physica Sinica, 2011, 60(1): 081501.) [36] 范子菡, 毕津顺, 罗家俊. 基于PDSOI单粒子翻转物理机制的SPICE模型研究[J]. 微电子学与计算机, 2011, 28(12): 40-45. (FAN Zi-han, BI Jin-shun, LUO Jia-jun. A study of physics-basis SEU SPICE model [J]. Microelectronics and Computer, 2011,28(12): 40-45.) [37] KAUPPILA J S, STERNBERG A L, ALLES M L, et al. A bias-dependent single-event compact model implemented into BSIM4 and a 90 nm CMOS process design kit [J]. IEEE Trans Nucl Sci, 2009, 56(6): 3 152-3 157. [38] YU T J, CHEN S M, CHEN J J, et al. Effect of supply voltage and body-biasing on single-event transient pulse quenching in bulk fin field-effect-transistor process [J]. Chin Phys B, 2016, 25(4): 049401. [39] HUANG P, CHEN S, CHEN J. Mechanism of floating body effect mitigation via cutting off source injection in a fully-depleted silicon-on-insulator technology [J]. Chin Phys B, 2016, 25(3): 036103. [40] TANG H K, CANNON E H. SEMM-2: A Modeling System for Single Event Upset Analysis [J]. IEEE Trans Nucl Sci, 2004, 51(6): 3 342-3 348. [41] MUNTEANU D, AUTRAN J L. Modeling and simulation of single-event effects in digital devices and ICs [J]. IEEE Trans Nucl Sci, 2008, 55(4): 1 854-1 878. [42] WELLER R A, REED R A, WARREN K M, et al. General framework for single event effects rate prediction in microelectronics [J]. IEEE Trans Nucl Sci, 2009, 56(6): 3 098-3 108. [43] WANG H B, BI J S, LI M L, et al. An area efficient SEU-tolerant latch design[J]. IEEE Trans Nucl Sci, 2014, 61(6): 3 660-3 666. [44] KHAN H, HOUNSHELL D, FUCHS E. Science and research policy at the end of Moore's law[J]. Nature Electronics, 2018, 1: 14-21. [45] TRACK E, FORBES N, STRAWN G. The End of Moore’s Law[J]. Computing in Science & Engineering, 2017, 19(2): 4-6. [46] INGEBRANDT S. Bioelectronics: Sensing beyond the limit[J]. Nature Nanotechnology, 2015, 10: 734-734. [47] DUTTA S, CHANG S, KANI N, et al. Non-volatile Clocked Spin Wave Interconnect for Beyond-CMOS Nanomagnet Pipelines[J]. Scientific Reports, 2015, 5: 9861. [48] MOU X, REGISTER L, MACDONALD A, et al. Bilayer Pseudospin Junction Transistor (BiSJT) for Beyond-CMOS Logic[J]. IEEE Transactions on Electron Devices, 2017, 64(11): 4 759-4 762. [49] THEAN A, COLLAERT N, RADU L, et al. Heterogeneous nano-to wide-scale Co-integration of beyond-Si and Si CMOS devices to enhance future electronics[J]. ECS Transactions, 2015, 66(4): 3-14.3.3 基于SPICE的数值仿真(简单的电路层级)[36-37]
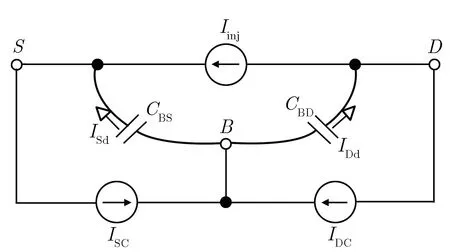
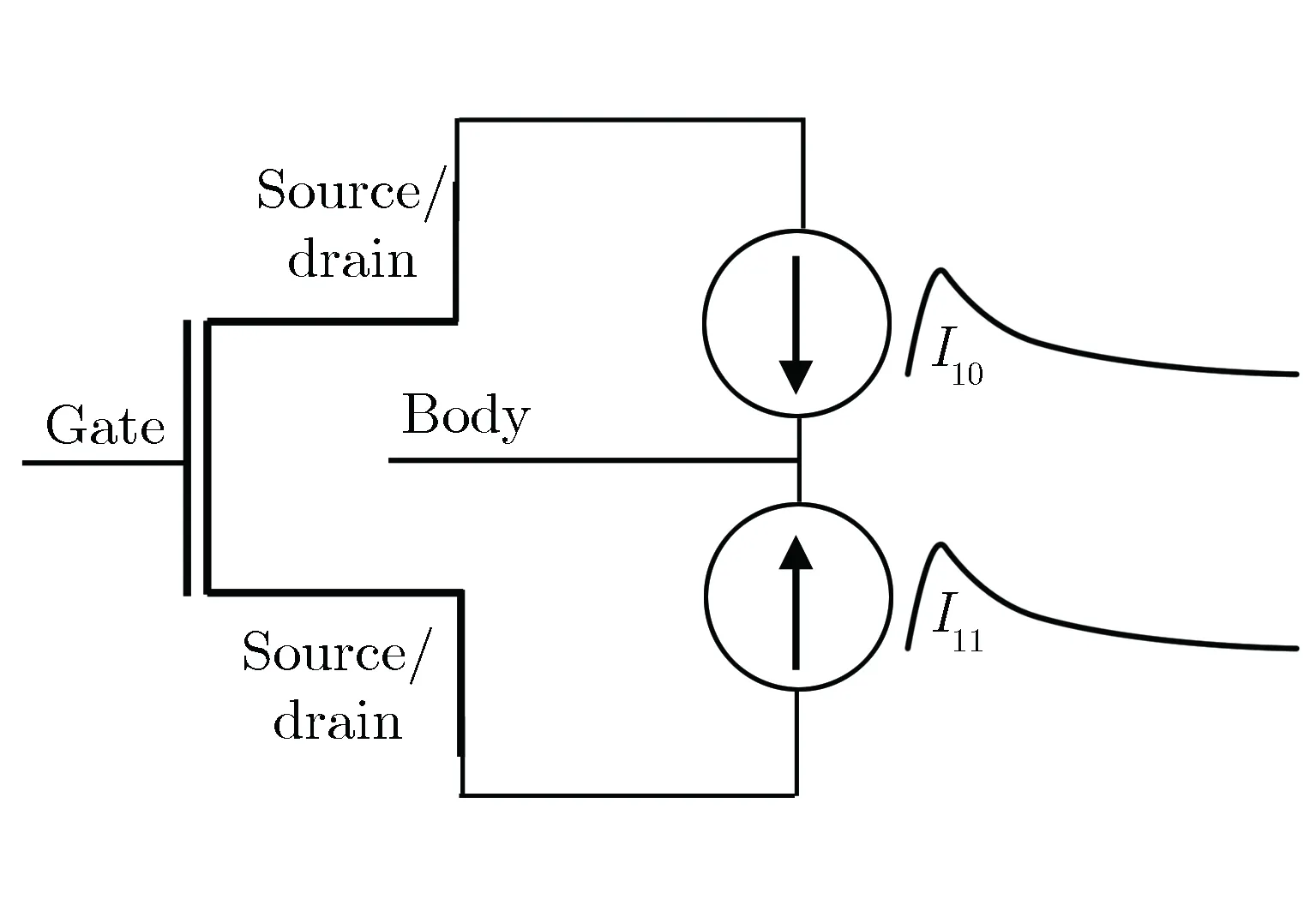
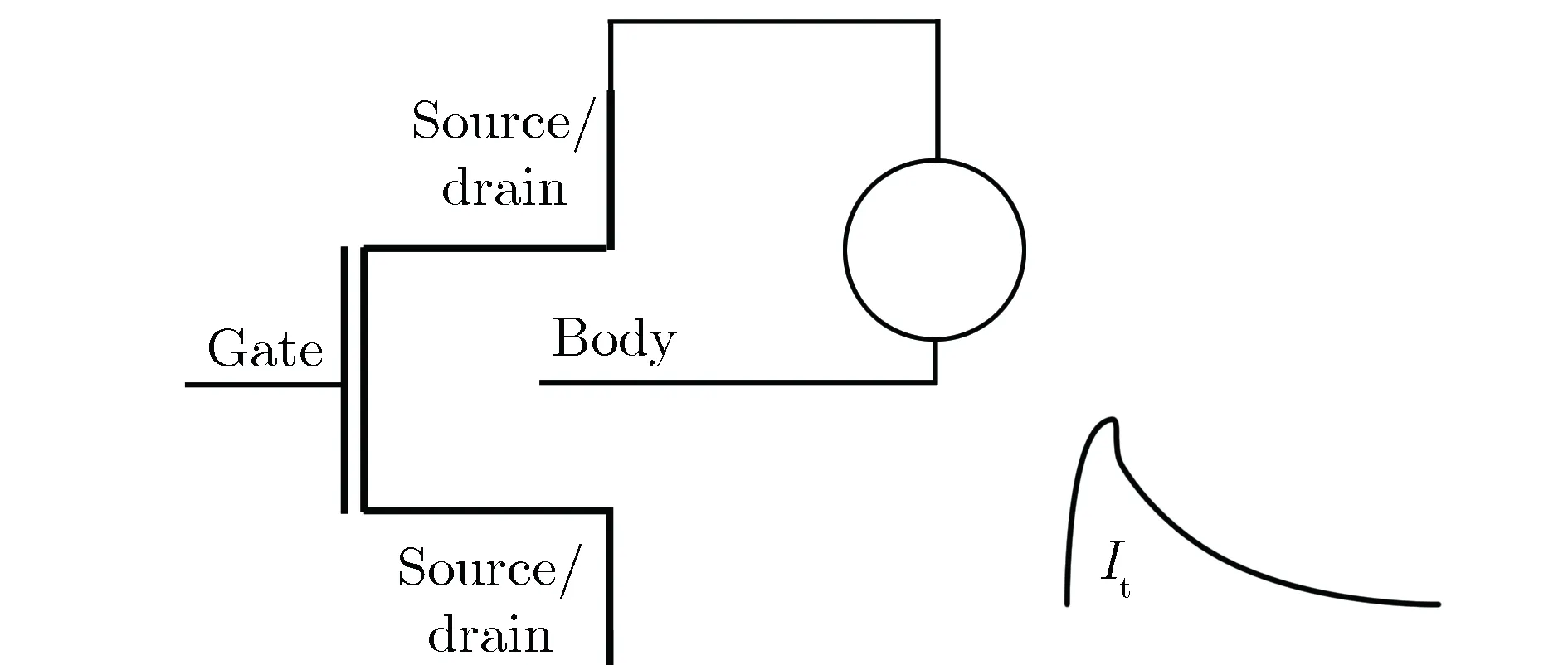

Fig.11ChargeinjectionmethodsinPowerSpice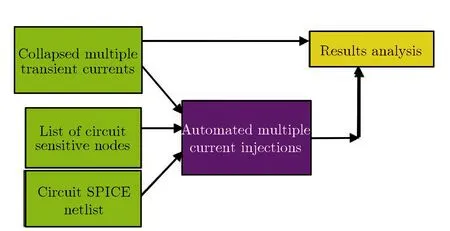
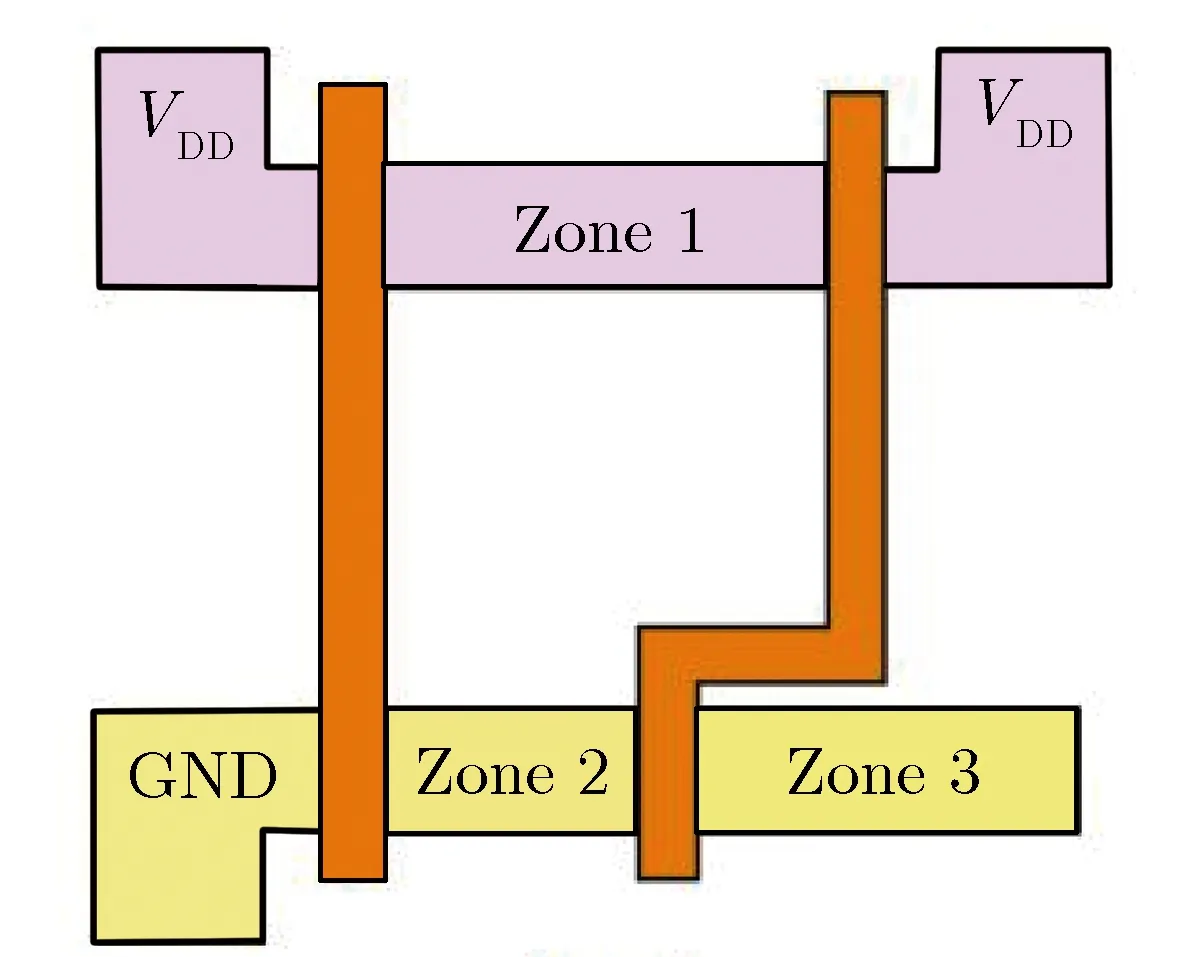
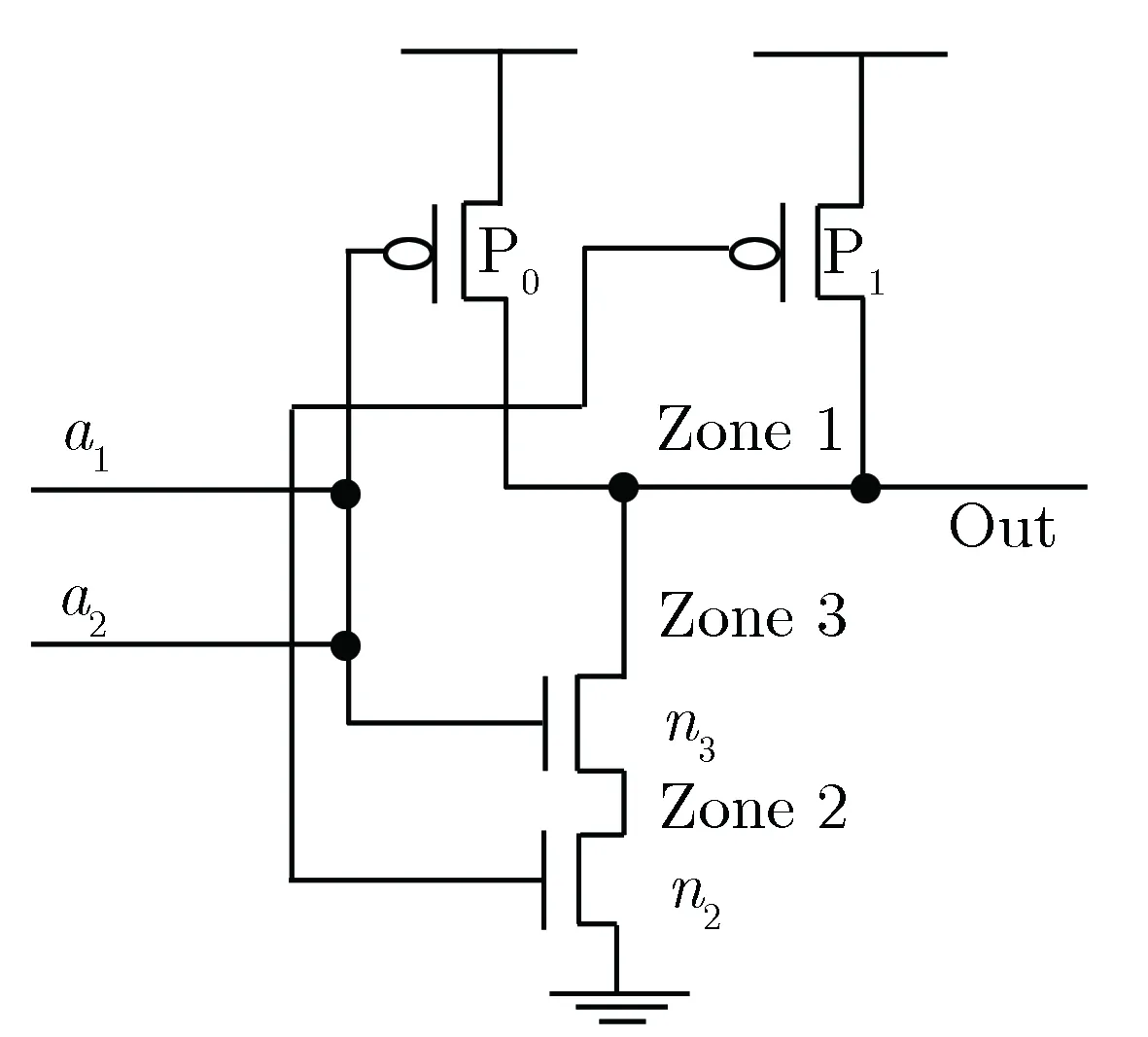
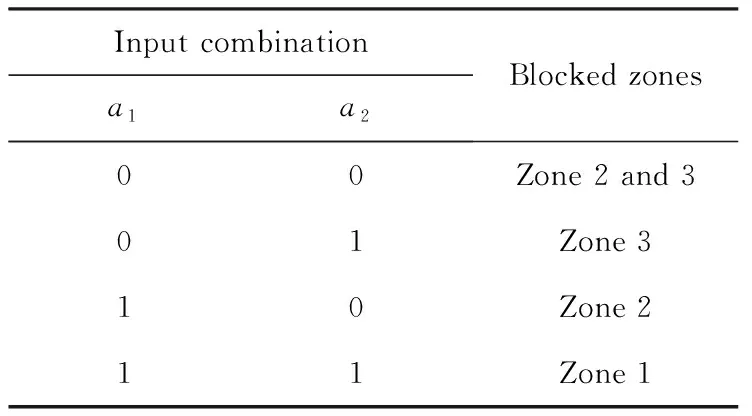

3.4 电路级和系统级的单粒子软错误的数值仿真[38-42]
4 趋势和展望[43-49]

