紫禁城平面布局中的几何构型分析初探

王 霞，王守民，张 静，梁昕宇

(西安工业大学 建筑工程学院，陕西 西安 710021)

紫禁城是中国古代建筑组群的优秀代表，凝聚着中国古代文明在古城规划和建筑学领域的智慧，蕴含着一定的科学道理。古希腊数学家、哲学家毕达哥拉斯(Pythagoras，约公元前580-约公元前500(490)年)在自然科学和几何学领域的贡献给古代建筑布局的几何构型研究提供了思路；现代科学技术的发展，特别是几何拓扑学领域的发展也为深入研究建筑组群平面布局提出了类似的思路。比如3、4、5三个数字之间的勾股关系，可以通过几何构型体现出比率；再比如由0，1，1，2，3，5，8，13……组成的斐波那契数列和0.618黄金分割比例通过数字构型体现出美观。由于圆形、三角形和方形是最基本的几何图形，因此本文将从平面布局的几何构型角度出发，探索紫禁城平面布局的一些特点。

紫禁城东西宽753米，南北深961米[1]32-33，紫禁城的轮廓宽度与深度之比为0.783。本文使用紫禁城卫星照片[2]45作为底图(图1)，做出圆形、三角形和长方形等基本几何构型，试图找出紫禁城中在以上三个基本构型上的分布特点。

图1 紫禁城电子地图

一、紫禁城平面布局圆形构型分析

首先以紫禁城的宽度和深度中心线交叉点为圆心，并以紫禁城深度为直径做圆，得到紫禁城电子地图圆形构型分析一(图2)。从图中可以看出，中轴线与圆形构型的北交点是神武门建筑；圆形构型的东北边线穿过北五所东北角、符望阁建筑、颐和轩建筑和庆寿堂建筑；圆形构型西北边线穿过建福宫花园西北角和英华殿建筑；中轴线与圆构型的南交点是午门建筑；圆构型东南边线通过东华门北侧、内阁大堂和内阁诰敕房南侧；圆形构型西南边线通过西华门北侧、激桶处东侧和翻书房南侧。

其次以紫禁城的宽度和深度中心线交叉点为圆心，并以紫禁城宽度为直径做圆，得到紫禁城电子地图圆形构型分析二(图3)。从图中可以看出紫禁城的宽度和深度中心(即圆心位置)是中轴线和中和殿北面最高层台基边沿线的交点；中轴线与圆形构型北交点是天一门建筑，而且过北交点的该圆形构型切线是北五所与东六宫之间的夹道；圆形构型北边线通过钟粹宫西北角和储秀宫东北角；而过中轴线与圆形构型的南交点做圆切线，则恰好与东华门和西华门的南边线走向一致；圆形构型的南边线分别通过内金水河与协和门北侧的交点，内金水河与熙和门北侧的交点，以及文华门和武英殿建筑。

图2 圆形构型分析一图3 圆形构型分析二

然后以紫禁城的宽度和深度中心线交叉点为圆心，并以紫禁城宽度为直径所做的圆形构型向北移动至圆心处于中轴线和景运门与隆宗门南侧边沿线交点时，获得紫禁城电子地图圆形构型分析三(图4)。可以发现：中轴线与圆构型北交点处是神武门建筑；圆形构型东边线经过南三所东南角，宁寿宫东北角；而中轴线与圆构型的南交点则是太和门建筑，此时过中轴线与圆形构型南交点做圆形的切线是东南崇楼与西南崇楼的北边线连线；该圆形构型西边线通过静怡轩建筑及寿安宫西北角。

再次以紫禁城的宽度和深度中心线交叉点为圆心，并以紫禁城宽度为直径所做的圆形构型向南移动至圆心处于太和殿建筑时，获得紫禁城电子地图圆构型分析四(图5)。可以看出当圆心移至太和殿建筑时，中轴线与圆形构型北交点处是坤宁宫建筑；过中轴线与圆构型北交点做圆形切线是养性殿建筑、永和宫主殿建筑、承乾宫主殿建筑、翊坤宫主殿建筑、长春宫主殿建筑和寿安宫主殿建筑的连线；该圆形构型的北边线通过宁寿门建筑，景仁宫东北角，永寿宫西南角，寿康宫正殿建筑；中轴线与圆形构型南交点落在了午门建筑处，该圆形构型南边线通过内阁大堂和咸安门建筑。

图4 圆形构型分析三图5 圆形构型分析四

最后在中轴线上以乾清门到午门为直径，再以乾清门到神武门为直径分别做两个圆，与图2和图3整合在一起，得到紫禁城电子地图圆形构型分析五(图6)。可以看出两个圆覆盖了紫禁城中轴线的主要宫区。

接下来，在中轴线上以乾清门到坤宁门长度为直径做圆，然后将相同直径的圆沿着中轴线依次外切分布，得到紫禁城电子地图圆形构型分析六(图7)；再将这五个圆整体向南移动，将最北点至神武门建筑，得到紫禁城电子地图圆形构型分析七(图8)；然后将平移前、后的圆形构型整合在一张图上，得到紫禁城电子地图圆形构型分析八(图9)。发现各等直径圆交点处，均分布有建筑物或者建筑物的边线。

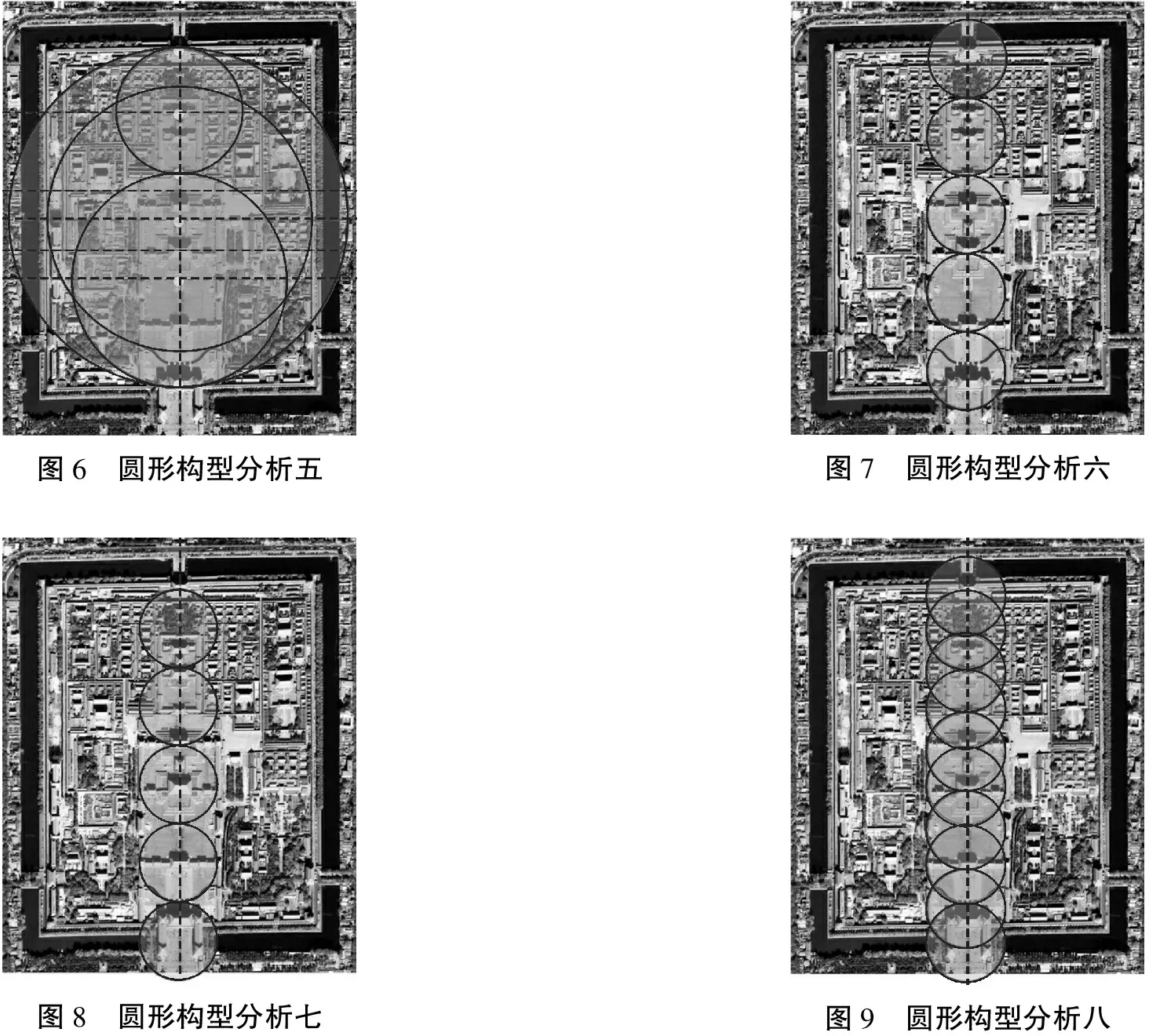
图6 圆形构型分析五图7 圆形构型分析六图8 圆形构型分析七图9 圆形构型分析八

二、紫禁城平面布局三角形构型分析

首先以紫禁城宽度为边长，分别以紫禁城南部两个角楼连线、北部两个角楼连线为底边做等边三角形，得到紫禁城电子地图三角形构型分析一(图10)。这两个等边三角形的六个顶点分别落在四个角楼建筑，太和殿台阶南端点和乾清宫台阶南侧；偏北的等边三角形几何形心落在交泰殿建筑处；偏南的等边三角形几何形心落在太和门北侧位置。

其次以紫禁城的深度为边长，分别以紫禁城东部两个角楼连线、西部两个角楼连线为底边做等边三角形，得到紫禁城电子地图三角形构型分析二(图11)。这两个等边三角形的六个顶点分别是四个角楼建筑，筒子河东、西两侧的外边沿处。

再分别找到这两个等边三角形的几何形心，得到紫禁城电子地图三角形构型分析三(图12)以及紫禁城电子地图三角形构型分析四(图13)。偏西的等边三角形几何形心与偏东的等边三角形几何形心分别落在北边两个崇楼南侧。

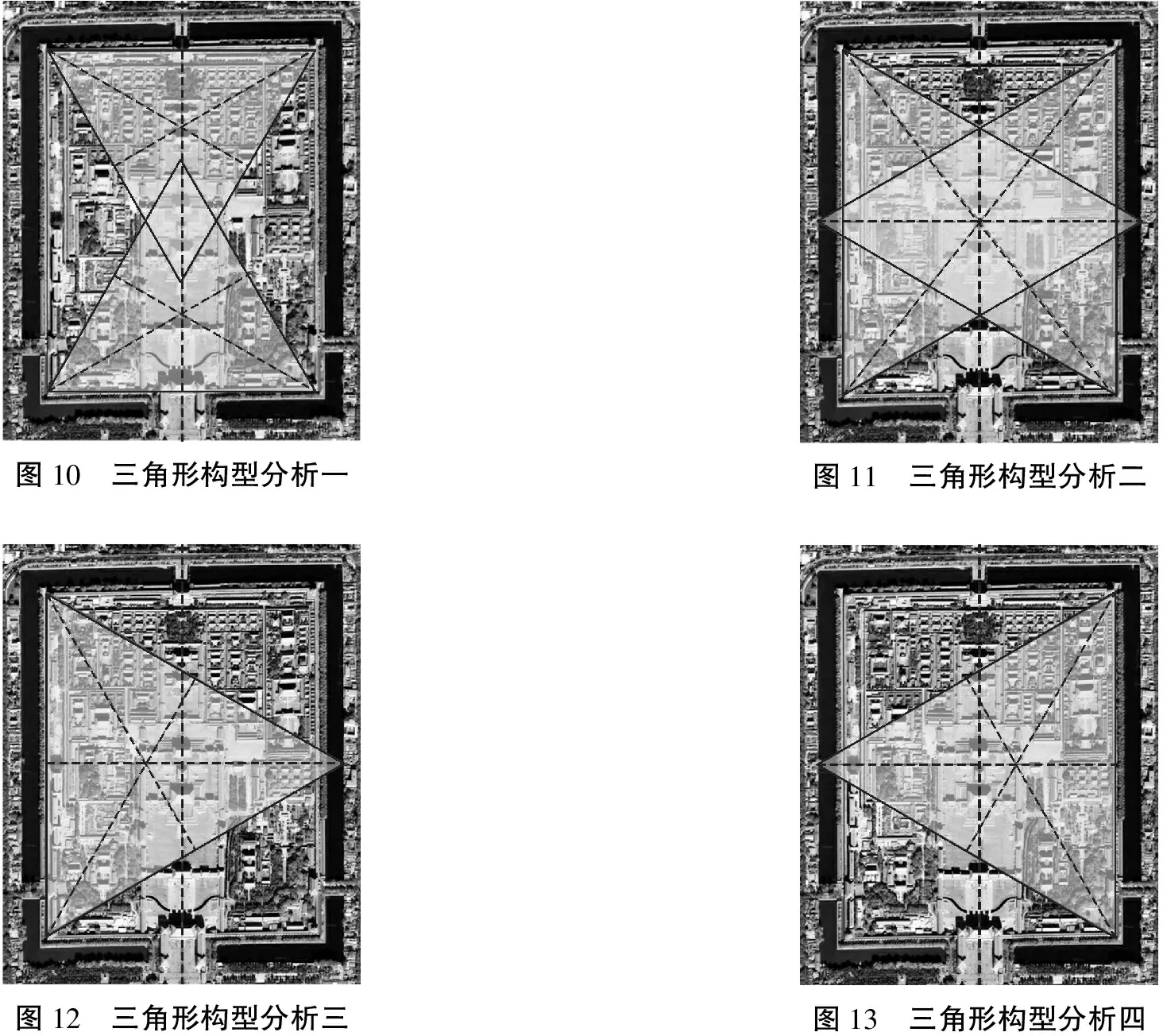
图10 三角形构型分析一图11 三角形构型分析二图12 三角形构型分析三图13 三角形构型分析四

然后将这四个等边三角形整合在一起，得到紫禁城电子地图三角形构型分析五(图14)。再次将崇楼宽度为边长做三个等边三角形，再以后两宫宽度为边长做两个等边三角形，得到紫禁城电子地图三角形构型分析六(图15)。可以看到这五个三角形的顶点位置处均是特定的建筑物。

图14 三角形构型分析五图15 三角形构型分析六

再将图15中的五个等边三角形倒置并向北移动，得到紫禁城电子地图三角形构型分析七(图16)。从图中可以看到这五个三角形的顶点位置处也有特定的建筑物。最后将上面的十个等边三角形整合到一张图上，得到紫禁城电子地图三角形构型分析八(图17)。

图16 三角形构型分析七图17 三角形构型分析八

三、紫禁城平面布局长方形构型分析

首先用长方构型在紫禁城电子地图(图1)中表示紫禁城的宽度和深度，该长方形宽度为14.3厘米，深度为18.25厘米，长方形宽度与深度之比为0.783，获得紫禁城电子地图长方形构型分析一(图18)。

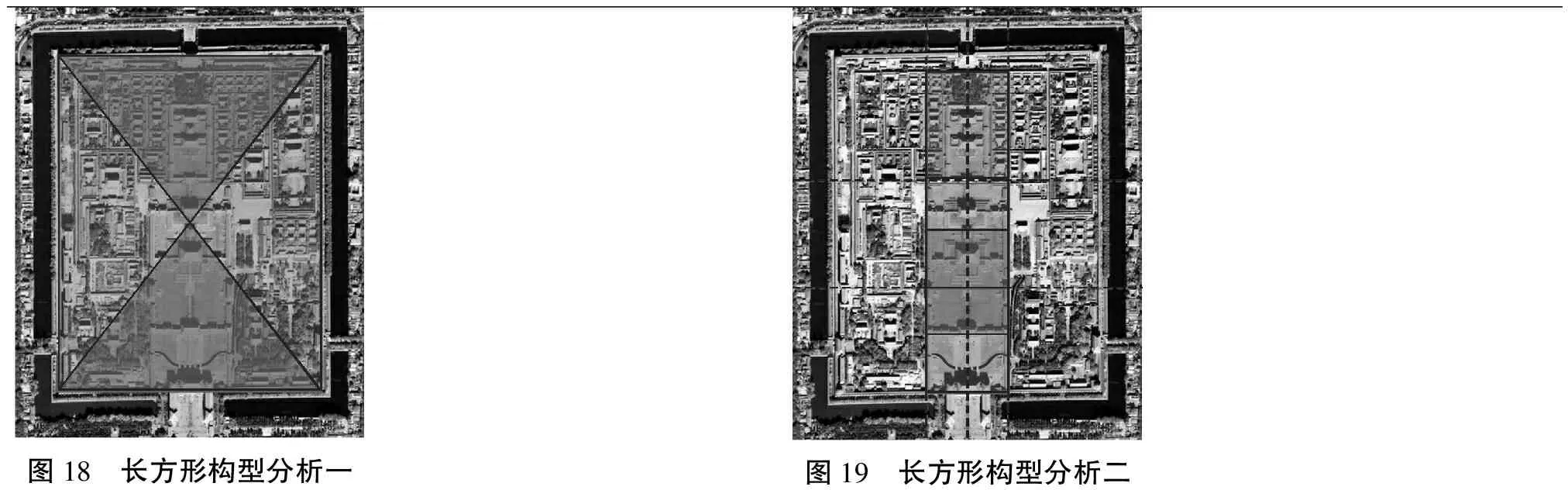
图18 长方形构型分析一图19 长方形构型分析二

再以崇楼东西之间的距离234米[1]32-33为宽度，按照宽度与深度比值为0.783，得到紫禁城电子地图长方形构型分析二(图19)中的四个相同尺寸的长方形，长方形宽度为4.44厘米，深度为5.67厘米。可以看出从午门到神武门，一共分布着三个同尺寸的长方形，最南边的长方形从午门到体仁阁与弘义阁北侧连线；中间的长方形从体仁阁与弘义阁北侧连线到乾清门建筑南侧；北边的长方形从乾清门建筑到顺贞门建筑，该长方形深度边长落在东二长街和西二长街上；从太和门到中和殿北侧，也分布着一个同尺寸的长方形。

其次以“后两宫”东西庑后檐墙距离118米为宽度，以乾清门前檐柱列和北端坤宁门后檐柱列计的距离218米为深度做长方形，该长方形宽度为2.24厘米，深度为4.18厘米，宽度与深度比值为0.535，长方形中心是乾清宫建筑；再以“前三殿”的东西宽，即东西角库之东西外墙234米为宽度，以太和门之前檐柱到乾清门之前檐柱距离437米为深度做长方形，该长方形宽度为4.44厘米，深度为8.29厘米，宽度与深度比值为0.535，长方形中心是太和殿建筑；最后以“前三殿”工字型台基东西宽129米，南北长232米[3]47做长方形，该长方形宽度为2.45厘米，深度为4.57厘米，宽度与深度比值为0.536，长方形中心是太和殿建筑北侧[1]32-33。同时，寿康宫长方形尺寸宽度为0.9厘米，长度为1.68厘米，宽度与深度比值为0.535。以上所做长方形见紫禁城电子地图长方构型分析三(图20)。

再次以四个崇楼围合的东西距离234米[1]32-33为宽度，南北距离353米为深度做长方形，该长方形宽度为4.44厘米，深度为6.70厘米，宽度与深度比值为0.663，长方形中心是太和殿台基南端；再以太和门庭院的东西距离200米为宽度，南北距离130米[4]28为深度做长方形，该长方形宽度为2.60厘米，深度为3.92厘米，宽度与深度比值为0.663，长方形中心是内金水桥北端。以上所做长方形如紫禁城电子地图长方形构型分析四(图21)所示。

图20 长方形构型分析三图21 长方形构型分析四

接着以太和殿至北面两个崇楼围合的东西距离234米[1]32-33为宽度，南北距离155米为深度做长方形，该长方形宽度为2.94厘米，深度为4.44厘米，宽度与深度比值为0.662，长方形中心是中和殿南端，如紫禁城电子地图长方形构型分析五(图22)所示。

再以“前三殿”工字型台基东西宽129米，南北长(计工字形本身，不计南面突出的月台)195米[1]32-33做长方形，该长方形宽度为2.52厘米，深度为3.80厘米，宽度与深度比值为0.663，长方形中心是中和殿建筑，如图紫禁城电子地图长方形构型分析六(图23)所示。

最后，将各部分按照功能分区得到紫禁城电子地图长方形构型分析七(图24)。可以看出，东、西六宫长方形、“后两宫”的乾清宫至坤宁宫围合长方形、乾清门到乾清宫台阶部分围合长方形、御花园长方形、英华宫长方形、寿安宫长方形、养性门北部长方形、文华殿区域长方形、武英殿区域长方形、养心殿与军机处围合长方形、斋宫长方形的宽度与深度比值在0.650～0.664之间。以上分析的长方构型尺寸与测量尺寸以及比例关系见表1。

将三大殿围合部分、后两宫围合部分及南三所围合部分做长方形得到紫禁城电子地图长方形构型分析八(图25)。从图中可以看出，三大殿围合部分、后两宫围合部分及南三所长方形的宽度与深度比值在0.837～0.838之间。以上图形中的长方构型尺寸与测量尺寸以及比例关系见表2。

图22 长方形构型分析五图23 长方形构型分析六图24 长方形构型分析七图25 长方形构型分析八

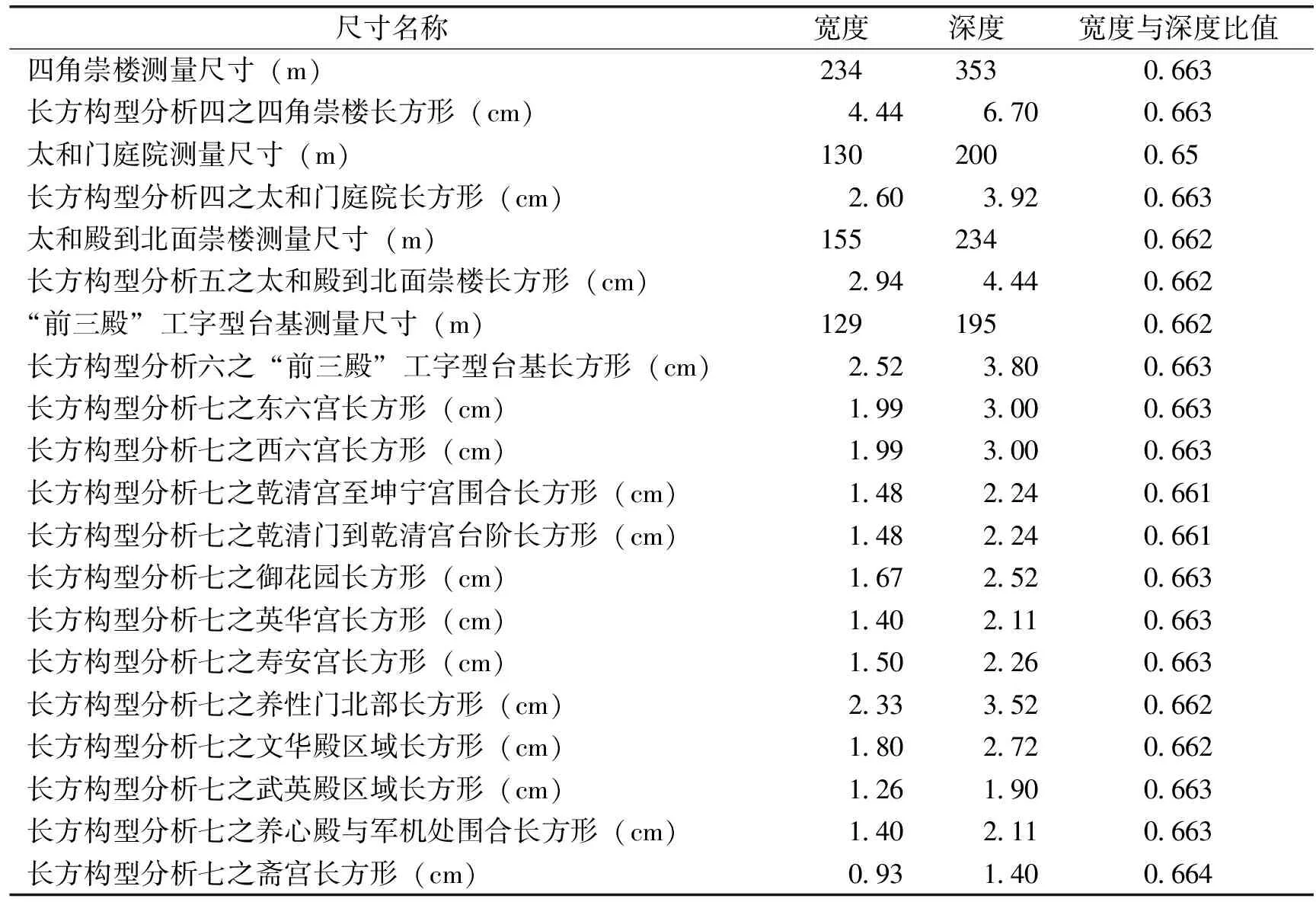
表1 长方构型宽度与深度比值为0.663的长方形尺寸

表2 宽度与深度比值为0.837的长方形尺寸

紫禁城的选址布局，疏密协调、宽窄相间，紫禁城变化差异中的对应、和谐、均衡不是在建筑美学的指引下完成的，而是在建筑理学的指引下完成的[5]13。建筑经过技术和艺术的巧妙结合和处理，化为空间的形式和秩序，它们就显示出巨大的魅力[6]57。紫禁城的设计者们对空间布局规划特征应该不会是偶然巧合，需要我们继续研究与探索。

四、结 语

在紫禁城平面布局圆形构型分析、三角形构型分析和长方形构型分析中，位于这三种几何构型特征点上，均布置有建筑物或者建筑物的边线。

在紫禁城平面布局长方形构型分析中，分别以宽度与长度之比为0.783，0.535，0.663和0.837四种情况的长方形作为构型单元，在每个比值下，均有若干区域成为相似的长方形构型。

紫禁城在数学上的几何构型尺寸和比率反映着建筑平面布局的规律，研究这些蕴含在几何学上的数学规律，可以为今后推测设计师在建筑布局上的哲学智慧提供研究基础。

参 考 文 献

[1]傅熹年. 中国古代城市规划、建筑群布局及建筑设计方法研究[M]. 2版. 北京：中国建筑工业出版社，2015.

[2]刘畅. 北京紫禁城[M].北京：清华大学出版社，2009.

[3]楼庆西. 中国古建筑二十讲[M].北京：生活·读书·新知三联书店，2004.

[4]赵广超. 大紫禁城——王者的轴线[M]. 香港:三联书店(香港)有限公司，2016.

[5]李文儒. 故宫院长说故宫[M].成都：天地出版社，2017.

[6]汪正章. 建筑美学：跨时空的再对话[M].南京：东南大学出版社，2014.