考虑地表径流拖曳力效应多层边坡稳定性分析

向云龙，符文熹，周洪福

(1.四川大学水利水电学院 水力学与山区河流保护国家重点实验室，成都 610065；2.中国地质调查局 成都地质调查中心，成都 610081)

降雨是导致滑坡发生的主要因素之一[1,2]，据统计，我国约90%的滑坡是由降雨直接或间接诱发的[3,4]由于降雨导致的滑坡灾害给国家造成了巨大的人员伤亡和财产损失。如四川茂县叠溪镇受连续多天降雨天气影响，2017年6月在新磨村发生的高位巨型滑坡，落差高达1 km，平面滑动距离3 km，造成河道淤堵，40余户被掩埋[5]。以往的研究表明，降雨引起的雨水入渗容易引起单层顺位滑坡[6-10]。针对多层滑坡，由于滑坡体各层面土力学强度参数的不同，位置各异，导致研究降雨对多层滑坡的影响非常复杂[11]。因此研究多层滑坡的稳定性对预防多层滑坡带来的自然灾害具有重大意义。强降雨不仅会导致斜坡土体饱和，土体强度降低，还会形成坡面径流和沟谷集中汇流。水的流动将对坡体产生拖拽作用，即拖曳力效应。学者们普遍认为当径流拖曳力大于边坡土壤临界拖曳力时，边坡土壤颗粒被剥蚀，从而影响边坡稳定性[12,13]。杨春霞等[14]研究了影响径流拖曳力的单因子，并指出边坡土壤剥蚀率与径流拖曳力单因子呈幂函数或指数函数, 边坡土壤剥蚀率随径流的增加呈增加趋势。吴卿等[15]研究了在一定坡度和流量条件下，裸坡、低覆盖度、高覆盖度坡面径流平均拖曳力大小关系。贺盛伟[16]以黄土区的主要土壤为研究对象，揭示了坡面径流流量和土壤类型的关系。边锋等[17]以黑土地为研究对象，研究了顺坡垄和无垄情况下降雨对边坡土壤的侵蚀过程。

拖曳力效应还广泛存在于土木工程中，如防洪堤和土石坝填筑体内发生的管涌和接触冲刷等渗透破坏都伴随有壁面拖曳力效应。有关拖曳力的研究，Stokes[18]在1851年给出了圆球在无限域黏性流体缓慢运动条件下拖曳力的解析解；Rumer[19]引入Stokes的拖曳力公式，通过土柱微元体受两端孔隙水压力、水流自重和土颗粒摩阻力作用下的力平衡分析，推求并很好地验证了线性层流状态Darcy理论；Chai[20]基于开口立方定律推导出单裂隙岩体壁面拖曳力表达式；水流拖曳力是边坡稳定性分析的组成部分，当边坡处于临界状态时，拖曳力有可能是“压死骆驼的最后一根稻草”，因此，拖曳力效应不容忽视。

由于以往分析降雨对多层边坡的影响鲜有考虑坡面径流产生的拖曳力作用。因此本文在前人研究的基础上，根据流体运动理论推求坡面径流对多层边坡产生的拖曳力，进而计入拖曳力进行多层边坡稳定性分析，研究拖曳力对多层边坡稳定性的影响大小，为全面准确评价多层边坡在降雨条件下的稳定性提供参考。

1 流场分析及切应力计算

1.1 模型建立

降雨形成的地表径流会对斜坡产生冲刷作用，这种作用随着水流强度的增加而不断增加，对斜坡稳定构成潜在威胁。本文以实际边坡为基础，概化出深层土、岩接触面斜坡渗流分析模型，如图1所示。模型中斜坡坡度为θ，长度为L，上部土层厚度为b1，孔隙率为n1，渗透率为K1，土体渗流沿x方向的流速为wx;下部土层厚度为b2，孔隙率为n2，渗透率为K2，土体渗流沿x方向的流速为vx;坡面径流高度为h，沿x方向的流速为ux。建立如图1所示平面直角坐标系xoy，x轴正方向为斜坡土层的倾斜方向，y轴正方向垂直于层面向上，并对该斜坡径流流场特征进行理论分析。

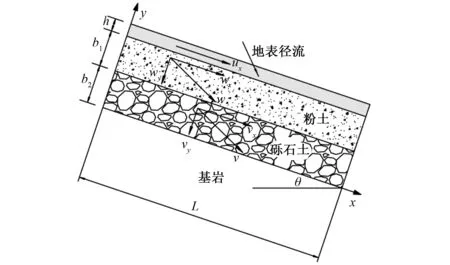
图1 多层滑坡理论分析模型Fig.1 Theoretical analysis model of multi layer landslide

实际上，天然流体的运动属于三维空间运动，其影响因素十分复杂。为研究方便，进行如下假设：①斜坡土层和径流均沿x方向无限延伸；②斜坡土体颗粒单一、均匀；③水流为二维平面运动，且沿y方向的流速为0；④水流为Newton流体，且为充分发展的层流； ⑤水流不可压缩，即满足连续性方程；⑥基岩为不透水层；⑦斜坡土体渗流可用Brinkman-extended Darcy方程描述，见式(1)；坡面径流用Navier-Stokes方程描述，见式(2)。

(1)

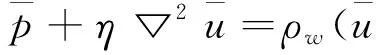
(2)

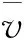
1.2 流场求解

1.2.1 径流流速求解

根据上述模型基本假设，坡面径流满足连续性方程和Navier-Stokes方程。

连续性方程写为：

(3)

式中：uy、uz分别为水流沿y方向和z方向的流速。

Navier-Stokes方程(沿x方向)写为：

(4)

式中：fx为沿x方向的质量力；P为沿x方向的压强；υ为水的运动黏滞系数，且υ=η/ρ。

由于水流沿y方向和z方向的流速均为0(即uy=uz=0)，故有∂uy/∂y=∂uz/∂z=0，将其带入式(3)可得∂ux/∂x=0；x方向流速ux在z方向不发生变化，即∂ux/∂z=0；沿x方向上，fx=gsinθ，dP/dx=-ΔP/L；水流为恒定流，可得∂ux/∂t=0。将这些条件代入式(4)并化简得：

(5)

式中：γw为水的容重。

求解式(5)得：

(6)

式中：A1、A2为待求系数。

1.2.2 渗流流速求解

根据分析模型的基本假设，斜坡上部土层的水流运动满足连续性方程和Brinkman-extended Darcy方程。

连续性方程写为：

(7)

式中：wy、wz分别为土体内水流沿y方向和z方向的流速。

Brinkman-extended Darcy方程(沿x方向)：

(8)

化简式(8)得：

(9)

求解式(9)得：

式中:B1和B2为待求系数。

同理，下部土层也满足式(7)连续性方程和式(8) Brinkman-extended Darcy方程，则有下部土体沿x方向渗流流速为：

式中:C1和C2为待求系数。

为方便进行计算，令：

(12)

则化简后式(6)、式(10)和式(11)可简化为：

(13)

1.2.3 边界条件

径流流速ux和土体渗流流速vx、wx满足以下边界条件。

(1)在径流上表面(y=b1+b2+h)处，径流流速ux达到最大，即满足dux/dy=0。

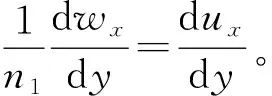
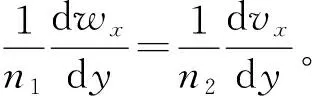
(4)在斜坡土层底部(y=0)处，满足vx=0。

将以上边界条件带入式(13)并令：

(14)

解得A1、A2、B1、B2、C1、C2的值如下：

(15)

1.3 径流条件下斜坡表面的切应力分析

由Newton内摩擦定律[23]可知：

(16)

式中：τ为切应力；u为流速。

把坡面径流流速ux代入式(16)，可求出径流沿x方向的切应力τx：

τx=η(2Ny+A1)

(17)

径流底部y=b1+b2处的τx即为水流对边坡坡面的切应力，记为τs，τs的具体表达如下：

τs=η[2N(b1+b2)+A1]

(18)

将式(12)的N和式(15)的A1带入式(18)，可得切应力的表达式为：

(19)

由于ΔP=γwΔH，而ΔH/L=i，且i=tanθ(i为水力坡降)，其中ΔH为土体两端水头差，故式(19)可化为：

τs=hγw(tanθ+sinθ)

(20)

分析式(20)可知：径流对边坡的切应力τs主要受径流水深h和边坡坡度θ的影响，且随径流水深h和坡度θ的增大而增大。

2 计入拖曳力的边坡稳定性分析

2.1 边坡上部土体稳定性分析

对边坡上部土体进行受力分析，如图2所示。土体所受的作用力包括：竖直向下的重力G1，竖直向上的浮力Fb1，沿坡面法向向上的支持力FN1，平行于坡面向下的拖曳力FD1和渗流力GD1，平行于坡面向上的摩擦力Ff1。

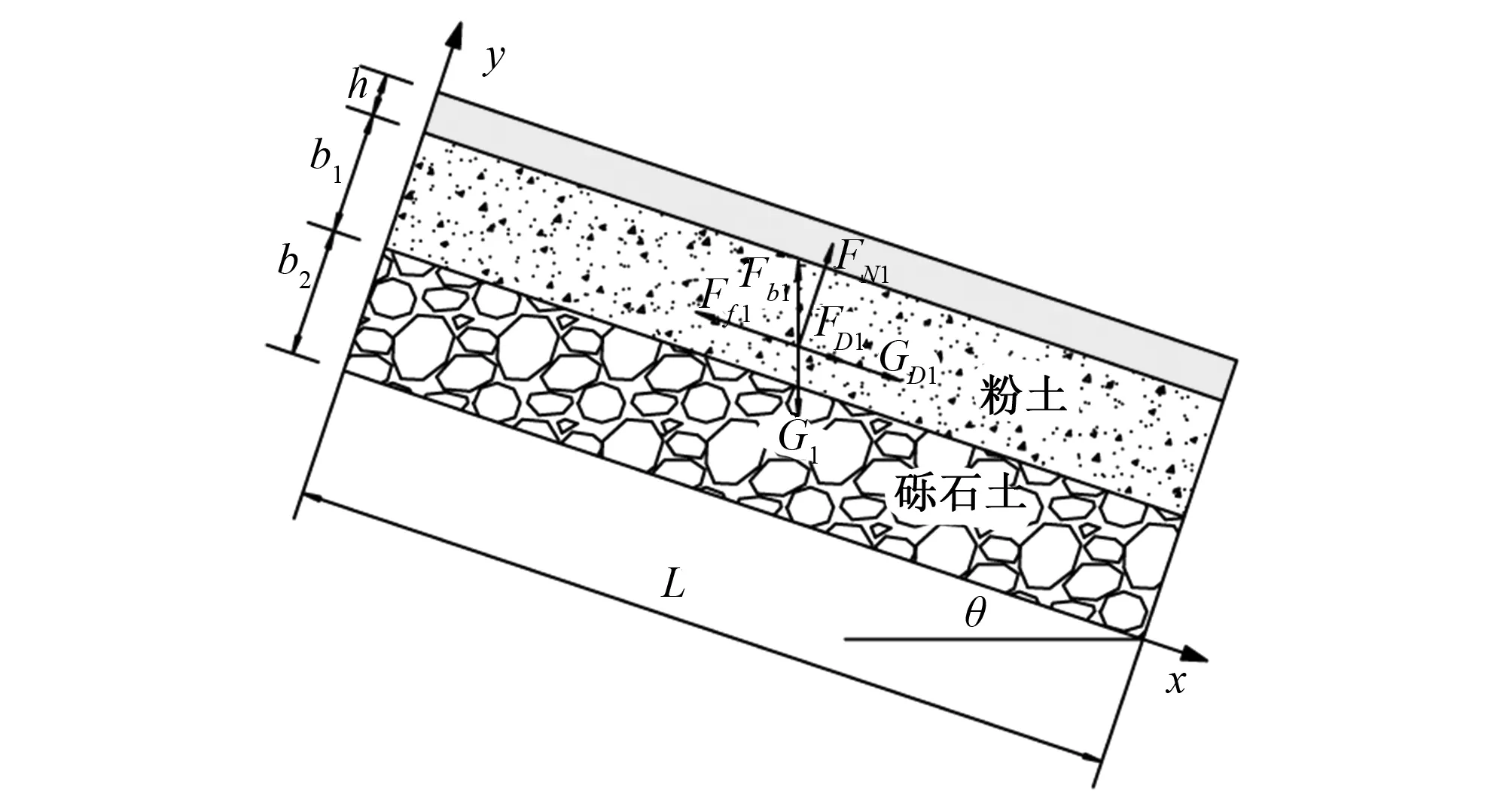
图2 上部土层受力分析图Fig.2 Analysis of upper soil stress

重力G1和浮力Fb1可由以下各式求出：

G1=b1Lγs1

(21)

式中：γs1为上部土体的重度。

Fb1=b1Lγw

(22)

由图2的受力分析可给出支持力FN1的表达式如下：

FN1=(G1-Fb1)cosθ

(23)

摩擦力Ff1为：

Ff1=FN1tanφ1+c1L=(G1-Fb1)cosθtanφ1+c1L(24)

式中：φ1为上部土体和下部土体的内摩擦角。

将式(21)和式(22)代入式(24)，整理得Ff1的表达式如下：

Ff1=b1L(γs1-γw)cosθtanφ1+c1L

(25)

求得径流对上部土体是我拖曳力FD1可见式(26)：

FD1=Lγwh(tanθ+sinθ)

(26)

渗流力GD1可由文献[22]中给定的方法求得：

GD1=tanθγwLb1

(27)

根据以上各式求得上部土体的安全系数Ks1见式(28)：

(28)

由式(28)可知，地表径流拖曳力FD1越大，则上部土层安全系数Ks1越小。对于坡体稳定性，拖曳力是一种不利因素，忽视这种作用将对工程安全产生不利影响。然而，在对边坡稳定性进行分析时考虑坡面径流拖曳力效应的文章却鲜有报道。

2.2 边坡下部土体稳定性分析

对边坡下部土体进行受力分析时，上部土体处以静力平衡状态。如图3所示。下部土体所受的作用力包括：竖直向下的重力G2，竖直向上的浮力Fb2，垂直于的支持力FN2，平行于坡面向上的摩擦力Ff2，流力GD2，上部土层施加的反作用的静摩擦力Ff3和反作用的支持力FN1。

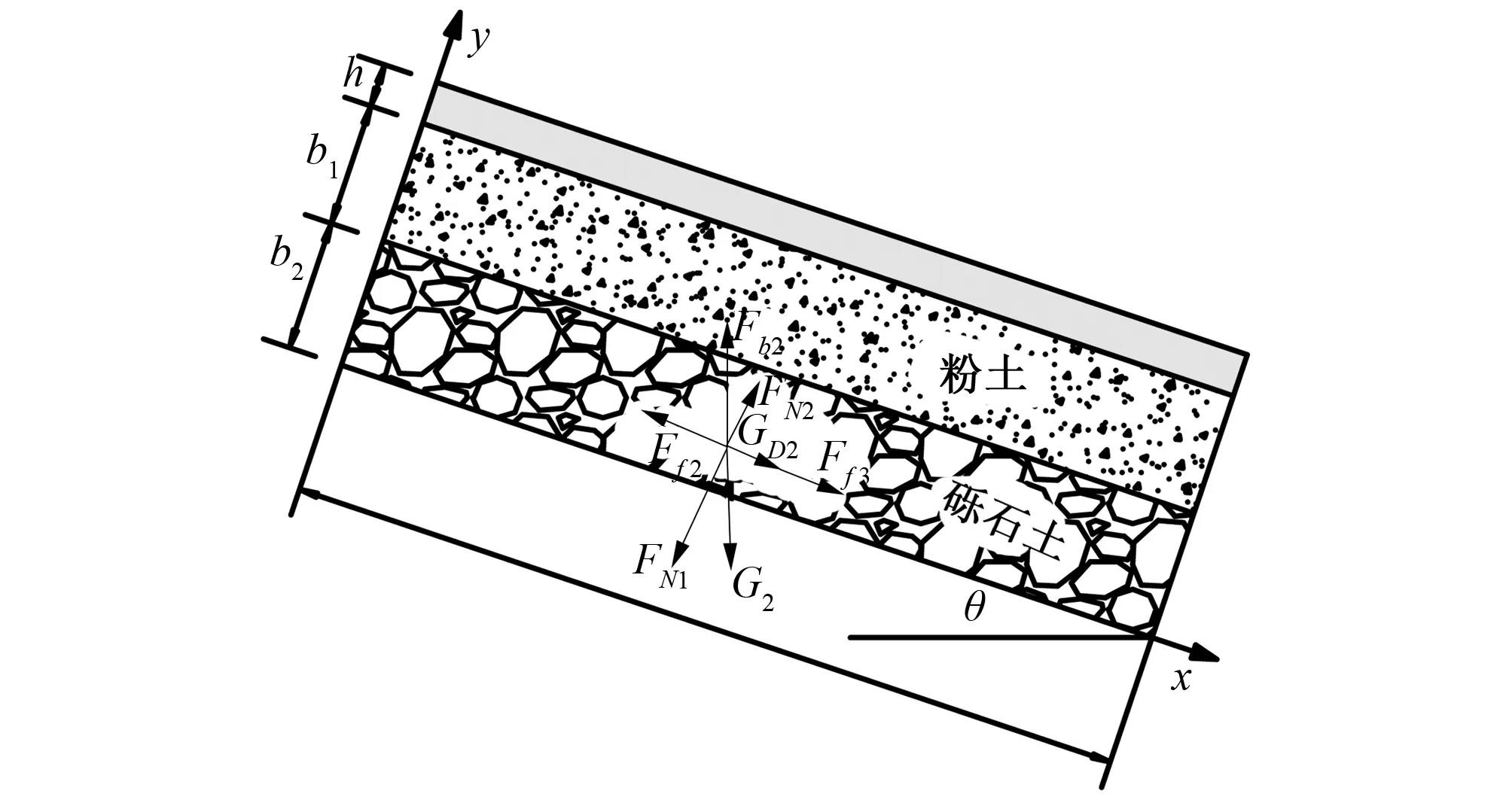
图3 下部土层受力分析图Fig.3 Analysis of lower soil stress

重力G2和浮力Fb2可由以下各式求出：

G2=b2Lγs2

(29)

式中：γs2为下部土体的重度。

Fb2=b2Lγw

(30)

由图2的受力分析可给出反作用的支持力FN1的表达式为式(23),持力FN2的表达式如下：

FN2=FN1+G2cosθ-Fb2cosθ=

(G1+G2)cosθ-(Fb1+Fb2)cosθ

(31)

摩擦力Ff2为：

Ff2=FN2tanφ2+c2L=(G1+G2)cosθtanφ2-

(Fb1+Fb2)cosθtanφ2+c2L

(32)

式中：φ2为下部土体和基岩的内摩擦角。

上部土体对下部土体的摩擦力的反作用力Ff3由上部土体的静力平衡求得，整理得Ff3的表达式如下：

Ff3=FD1+GD2-Fb1sinθ=γwLtanθ(h+1)-

γwLsinθ(h-b1)

(33)

下部土体的渗流力GD2表达式为：

GD2=tanθγwLb2

(34)

根据以上各式求得下部土体的安全系数Ks2见式(35)：

(35)

由式(35)可知，地表径流拖曳力FD1会直接影响上部土体对下部土体的静摩擦力Ff3，从而间接影响下部土体的稳定性。FD1越大，静摩擦力Ff3越大。下部土体的滑动力越大。土体更易失稳破坏。

3 工程实例分析与讨论

3.1 工程概况

本文选取四川遂宁地区遂安快速通道某道路旁一处土、岩接触面边坡为例(见图4)。

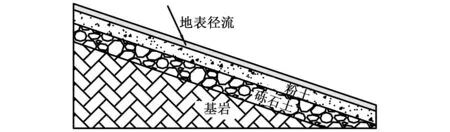
图4 遂宁地区某道路边坡示意图Fig.4 Scenic map of road slope at somewhere in Suining area

该边坡厚度约为4.95 m，上部土层粉土厚度约为1.5 m的粉土，下部土层厚度约为3.45 m的砾石土层。砾石土下覆不透水的基岩，由于四川地区常发生降雨，且强降雨较多，易于形成坡面径流。因此，本文采用上述分析方法求解地表径流对坡体的拖曳力，并利用刚体极限平衡理论对该边坡两层土体分别进行稳定性分析。其中，斜坡与坡面径流相关参数如表1所示。

表1 土体及径流相关参数Tab.1 Related parameters of soil and runoff

3.2 结果分析与讨论

计算结果表明，当不考虑坡面径流拖曳力时，此边坡上部土体的稳定系数为1.02，下部土体的稳定系数为1.23；当考虑坡面径流拖曳力时，此边坡上部土体的稳定系数为0.92，下部土体的稳定系数为1.18；上部土体的安全系数下降了9.95%，下部土体的安全系数下降了4.99%。

径流冲刷使坡面产生跌坎、细沟和浅沟，本次分析径流平均高度h与上下部土层安全系数的关系，得到图5。

图5 径流平均高度与安全系数的关系Fig.5 The relationship between runoff depth and safety coefficient

由图5可知安全系数Ks随着h的增大而减小，当h=0m时，上部土层的安全系数为1.02，下部土层的安全系数为1.23；而当h增加到0.2 m时，上部土层安全系数降低到0.92，降低了9.8%；下部土层安全系数降低到1.17降低了4.9%。这就说明径流平均高度对边坡稳定性具有显著影响，间接反映出降雨强度对边坡稳定性的不利作用。虽然坡面径流对边坡稳定的影响比软化作用的影响要小；但在临界稳定状态时，较小的拖曳力却会发挥决定性作用，导致边坡失稳。

在工程实践中，边坡的坡度往往对边坡的稳定性起着决定性的作用。通过计算分析得到边坡坡度与上下部土层稳定系数的关系，如图6所示。

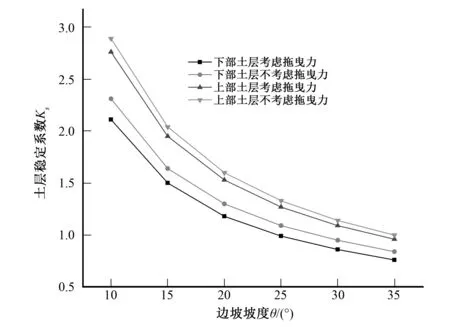
图6 边坡倾角与安全系数的关系Fig.6 The relationship between slope inclination and safety coefficient

图6表明，随着斜坡倾角的增加斜坡的上下部土层的安全系数不断降低，针对上部土层，考虑拖曳力时，安全系数从(θ= 20°)时的1.18降到(θ= 30°)时的0.86，降低了27.12%；不考虑拖曳力时，安全系数从(θ= 20°)时的1.3降到(θ= 30°)时的0.95，降低了26.92%。当边坡坡度为25°的时候，上部土层处于临界状态。当边坡坡度为35°的时候，下部土层处于临界状态。因此，在其他条件相似的条件下，斜坡越陡，存在水流拖曳力时，斜坡土体越不稳定。

土体的厚度也会对土体的稳定性产生影响，图7表明了上部土体稳定性随上部土体厚度的变化，土层厚度越大，土体稳定性越大。拖曳力直接作用在上部土层，当径流高度一定时，拖曳力也一定；上部土层越厚，抗滑力越大，土体就越稳定。当径流高度为0.2 m时，上部土体厚度大于3 m时，土层才稳定；当径流高度为0.15 m时，上部土体厚度大于2.7 m时，土层才稳定；当径流高度为0.1 m时，上部土体厚度大于2.4 m时，土层才稳定；当径流高度为0.05 m时，上部土体厚度大于1.8 m时，土层才稳定。图8给出了径流高度一定时，土体处于临界状态时土层厚度。曲线以上区域为对应径流高度的不敏感土层厚度。图9表明了下部土体稳定性随下部土体厚度的变化情况。拖曳力间接作用下下部土体，下部土体厚度越大，保水性就越强，土体软化效应越明显。自重增加导致沿坡面的滑动力增加，导致土体失稳。

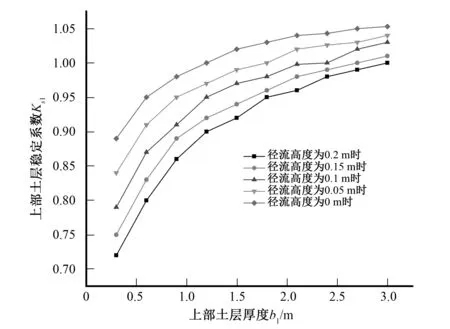
图7 上部土体厚度与安全系数的关系Fig.7 The relationship between thickness of upper soil and safety factor

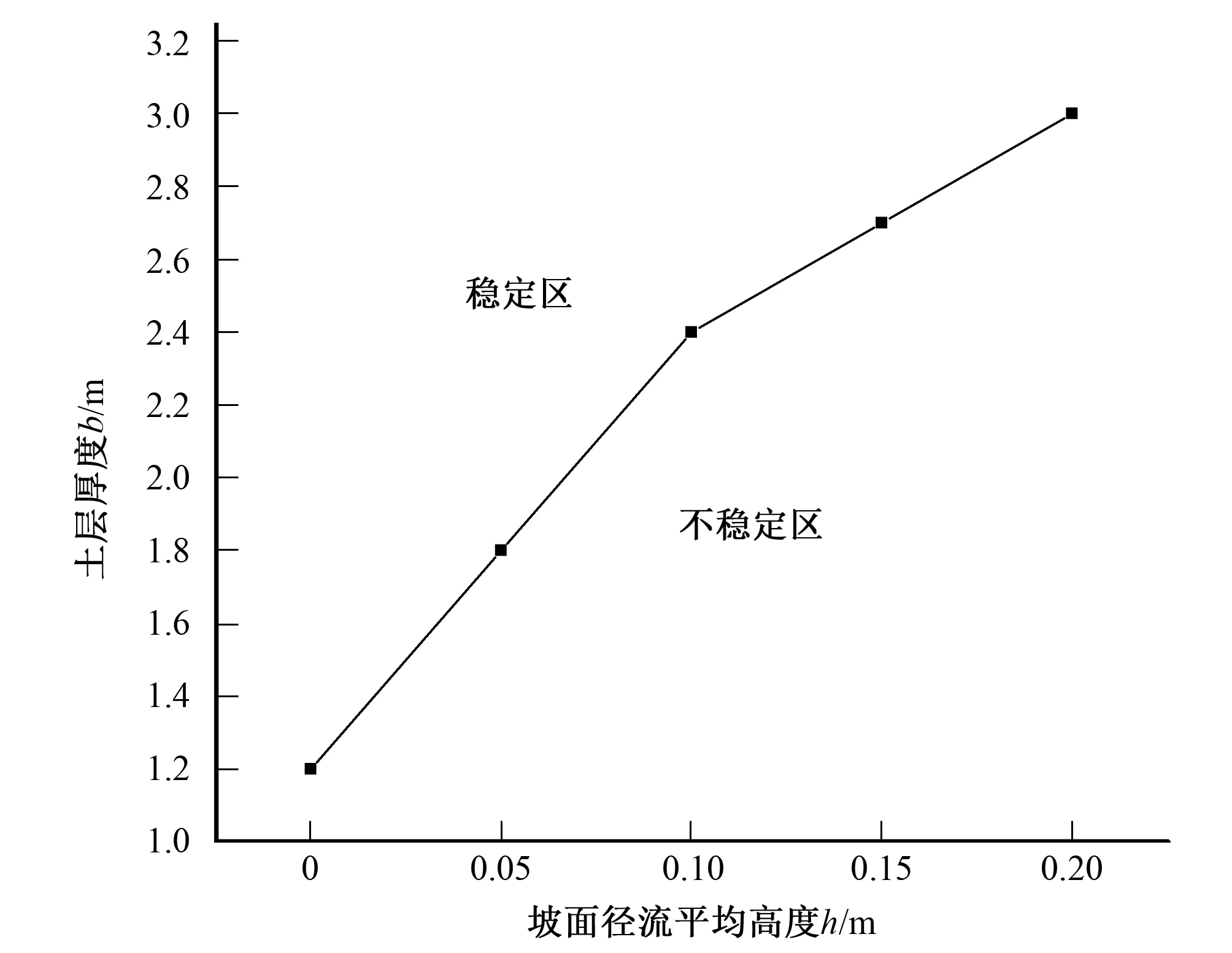
图8 径流平均高度与临界土层厚度的关系Fig.8 The relationship between average runoff height and critical soil thickness

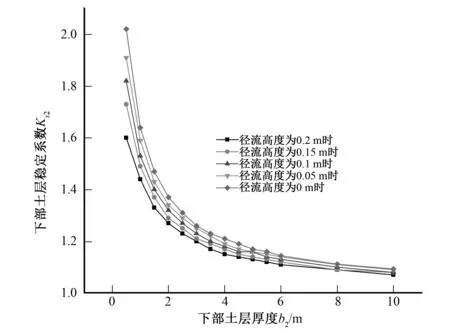
图9 下部土体厚度与安全系数的关系Fig.9 The relationship between the thickness of the lower soil and the safety factor

4 结 语

本文通过对地表径流拖曳力进行理论分析，并结合案例的讨论对比，得出以下结论：

(1) 坡面径流的拖曳力主要受径流水深h和边坡坡度θ的影响，且随径流水深h和边坡坡度θ的增大而增大。由此可见，降雨强度越大，水流拖曳力越大，边坡土体越容易失去稳定。

(2) 相对于降雨的软化作用，地表径流拖曳力效应对边坡稳定性的影响较小，但是当边坡处于临界稳定状态时，较小的拖曳力却会发挥决定性作用，导致边坡失稳，成为“压死骆驼的最后一根稻草”。

(3) 进行工程实例分析，考虑坡面径流拖曳力效应时，上下部土层的抗滑稳定安全系数均不同程度减小。多层边坡的理论分析、物理试验和数值计算，应将拖曳力嵌入进行稳定极限平衡分析。可将径流拖曳力纳入与地表径流有关的各类建(构)筑物稳定安全评价中加以推广应用。

(4) 径流高度的变化对上部土层的影响更加显著。在其他条件相同的情况下，边坡安全系数随着边坡坡度的增加而不断降低；边坡上部土层安全系数随着土层厚度的增加而不断增加，下部土层安全系数随着土层厚度的增加而不断减小。

□

参考文献：

[1] 李 卓,何勇军,盛金保,等.降雨与库水位共同作用下近坝库岸边坡滑坡模型试验研究[J]. 岩土工程学报, 2017,39(3):452-459.

[2] 徐永强,祁小博,张 楠.基于降雨与库水位耦合的三舟溪滑坡渗流模拟及稳定性分析[J]. 水文地质工程地质, 2016,43(5):111-118.

[3] 李 媛,孟 晖,董 颖,等.中国地质灾害类型及其特征----基于全国县市地质灾害调查成果分析[J]. 中国地质灾害与防治学报, 2004,15(2):29-34.

[4] 许建聪,尚岳全,陈侃福,等. 强降雨作用下的浅层滑坡稳定性分析[J]. 岩石力学与工程学报, 2005,24(18):3 246-3 251.

[5] 闻 越.解读四川茂县 “6· 24” 特大山体滑坡灾害成因[J]. 中国减灾, 2017,(7):26-29.

[6] 胡其志, 周 辉, 肖本林,等. 水力作用下顺层岩质边坡稳定性分析[J]. 岩土力学, 2010,31(11):3 594-3 598.

[7] Ng C W, Wang B, Tung Y K. Three-dimensional numerical investigations of groundwater responses in an unsaturated slope subjected to various rainfall patterns[J]. Canadian Geotechnical Journal, 2001,38(5):1 049-1 062.

[8] Ng C W W, Shi Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage[J]. Computers & Geotechnics, 1998,22(1):1-28.

[9] Rahardjo H, Li X W, Toll D G, et al. The effect of antecedent rainfall on slope stability[M]∥ Unsaturated Soil Concepts and Their Application in Geotechnical Practice. Springer Netherlands, 2001:371-399.

[10] Tsaparas I, Rahardjo H, Toll D G, et al. Controlling parameters for rainfall-induced landslides[J]. Computers & Geotechnics, 2002, 29(1):1-27.

[11] 杨 涛, 周德培, 罗阳明,等.考虑层间作用的多层滑坡分析方法[J]. 岩石力学与工程学报, 2005,24(7):1 129-1 133.

[12] Lyle W M, Smerdon E T. Relation of compaction and other soil properties to erosion resistance of soils[J]. Transactions of the ASAE,1965, 8(3):419-422.

[13] Foster G R, Meyer L D. Transport of soil particles by shallow flow[J]. Amer Soc Agr Eng Trans Asae, 1972,51(5):99-102.

[14] 杨春霞, 姚文艺, 肖培青,等. 坡面径流剪切力分布及其与土壤剥蚀率关系的试验研究[J]. 中国水土保持科学, 2010,8(6):53-57.

[15] 吴 卿, 杨春霞, 甄 斌,等. 草被覆盖对坡面径流剪切力影响的试验研究[J]. 人民黄河, 2010,32(8):96.

[16] 盛贺伟. 黄土区土壤类型和坡度对坡面片蚀和细沟侵蚀的影响研究[D]. 陕西杨凌：西北农林科技大学, 2016.

[17] 边 锋, 郑粉莉, 徐锡蒙,等. 东北黑土区顺坡垄作和无垄作坡面侵蚀过程对比[J]. 水土保持通报, 2016,36(1):11-16.

[18] Wilson HJ. Stokes flow past three spheres [J]. Journal of Computational Physics, 2013,245:302-316.

[19] Rumer RR, Drinker PA. Resistance to laminar flow through porous media[J]. Journal of the Hydraulics Division, 1966,92:155-163.

[20] Chai J. Drag forces applied on rock matrix by fluid flow through fracture network in rock mass[M]∥ Computational Methods in Engineering & Science, 2006:291.

[21] Neale G, Nader W. Practical significance of brinkman's extension of Darcy's law: Coupled parallel flows within a channel and a bounding porous medium[J]. Canadian Journal of Chemical Engineering, 2009,52(4):475-478.

[22] 李仕雄, 姚令侃, 蒋良维. 松散边坡演化特征及其应用[J]. 四川大学学报(工程科学版), 2004,36(2):7-11.

[23] 杨进良. 土力学[M]. 4版. 北京：中国水利水电出版社, 2009:76-77.