典型电容近炸引信发火控制部件储存寿命预测方法
齐杏林,王洪岩,吴英伟
(1.陆军工程大学石家庄校区,河北 石家庄 050003;2.中国白城兵器试验中心,吉林 白城 137001)
0 引言
在引信设计寿命周期内,储存环境会使发火控制部件内元器件的某些参数会发生漂移,如果性能变化影响到其功能,会导致引信近炸失效。因此,对典型电容近炸引信发火控制部件储存寿命进行准确预测具有重要意义。在引信寿命预测方面,文献[1]通过建立GM(1,1)模型和残差修正模型,推导出对引信系统寿命预测的改进算法。文献[2]将引信在湿热环境中储存,通过打靶检测获取引信失效数据,进而利用可靠性试验数据处理的方法获引信寿命。文献[3]运用Matlab软件分别拟合储存温度、湿度与引信寿命的曲线关系,通过建立模型并计算引信寿命。文献[4]采用加速寿命试验的方法获取引信失效数据,利用Arrhenius方程外推求出正常应力状态下引信寿命。这些方法基本达到了引信寿命预测的目的,但在寿命预测过程中仅考虑了加速寿命数据或储存环境等表象信息,缺乏引信自身指标参数退化致使引信失效分析。本文针对上述问题,并结合目前对引信发火控制部件储存性能退化研究较少,储存质量变化规律尚不明确的现状,提出了基于性能退化试验的引信发火控制部件寿命预测方法。
1 基于储存性能试验的寿命预测方法
1.1 基于储存性能试验的寿命预测一般步骤
产品的功能状况可以由其性能参数变化程度来表示,随着储存时间的增加,性能参数往往会产生变化,其功能状态也会发生改变,因此可以利用产品储存过程中性能参数的变化来进行寿命预测[5]。基于储存性能试验的寿命预测方法首先应通过储存性能试验获得其退化数据,找到性能退化敏感参数,选取性能退化分布模型,然后通过数据处理确定退化轨迹模型,进而预测发火控制部件的储存寿命。寿命预测步骤如下:
1) 进行发火控制部件储存性能试验,收集性能退化数据;
2) 确定性能退化敏感参数,结合产品相关性能指标确定失效阈值;
3) 采用分布假设检验法选取性能退化分布模型;
4) 数据处理计算相关参数,利用最小二乘法估计参数方程曲线的系数求出性能退化轨迹模型;
5) 最后,将性能退化轨迹模型带入退化分布模型结合产品失效阈值和可靠度即可预测发火控制部件寿命。预测流程如图1所示。
1.2 性能退化敏感参数的确定
为了判断产品的退化情况,通常选取几个主要的指标作为性能退化敏感参数,当其中一个或多个参数超过失效阈值时即发生失效。在选取性能退化敏感参数时,一般应满足下列条件:
1) 有明确的定义且易于监测;
2) 退化量数据可以进行统计处理;
3) 在实际应用上能提供相关设计信息;
4) 随着时间的增加参数变化程度和趋势明显,能很好体现出产品性能状态。
1.3 性能退化分布模型及退化轨迹模型
常见的与引信同类型的高可靠长寿命产品性能退化分布模型有正态分布模型和威布尔分布模型[6]。
正态分布模型:当y≥Df时产品发生失效,就可以得到产品可靠性与性能退化量分布之间的关系为:
(1)
当y≤Df时产品发生失效,可以得到产品可靠性与性能退化量分布的关系为:
(2)
威布尔分布模型:当y≥Df时产品发生失效,产品可靠性与性能退化量分布的关系为:
(3)
当y≤Df时产品发生失效,产品可靠性与性能退化量分布的关系为:
(4)
式(1)—式(4)中,y为性能退化量;Df为产品失效阈值;μy(t)为样本均值;σy(t)为样本均方差;my(t)为形状参数;ηy(t)为尺度参数;R(t)为可靠度。
退化轨迹模型可以很好的描述产品性能退化的过程。常见的有线性、凸型和凹型三种退化轨迹模型[7],通常可以通过对数转换等方程变形将凸型和凹形退化轨迹模型都转换为线性模型,并大大简化分析过程。
2 发火控制部件储存性能试验及结果分析
发火控制部件储存性能试验结合该电容近炸引信相关性能要求确定试验检测项目;依据各部件工作原理结合模拟信号确定检测方法并进行相关参数检测;根据统计分析需要和相关国军标确定试验样本量。
2.1 发火控制部件检测项目及检测方法
发火控制部件是指由探测器、定时器等组成的部件。参考该电容近炸引信在生产验收过程中性能要求确定主要检测定时器部件的定时器电流ID、接电时间TJ、工作电流IG、系统功能FX和探测器部件的检波电压VJ、点火脉冲宽度PW、炸高H共7项目[8],检测项目及含义如表1所示。
表1 发火控制部件检测项目及含义
Tab.1 Testing item and meaning of firing control unit

部件名称检测项目含义定时器部件定时器电流ID定时器接电前输入的直流电流接电时间TJ从开始输入电压到定时器计时完成并接电为下级电路提供工作电压所经过的时间工作电流IG定时器接电后正常工作输入的直流电流系统功能FX目标仿真信号作用到引信上时雷管座上测到的点火脉冲宽度及幅值探测器部件检波电压VJ弹目距离信息的电容变化转化成的电压信号点火脉冲宽度PW作用到雷管上的点火脉冲炸高H一定仿真落速下引信炸高
用专用扳手从引信中旋出安保机构和传爆序列,拧出连接引信体和风帽体的四个铆接螺钉,并分离引信体和电子头,取出电雷管和击针,再将电子头装入不含电雷管和击针的引信体中,成待测状态,即为发火控制部件。将装定一定时间的发火控制部件放入综合参数仿真测试系统中,输入目标仿真信号,即可测量定时器部件的定时器电流ID、接电时间TJ、工作电流IG、系统功能FX。
将检测后的发火控制部件电子头和引信体重新分离,用台式钻床钻掉定时器部件上焊点,取下定时器部件和电源部件即为探测器部件。将探测器部件放入仿真箱中,将目标仿真信号作用到探测器上,测量检波电压VJ和点火脉冲宽度PW;按照规定落速将目标信号作用到探测器上,对其进行仿真测试,计算160 m/s,220 m/s,280 m/s和340 m/s四种典型仿真落速下的对应炸高,并分别记为H1,H2,H3,H4。
2.2 样本量确定
为考核引信在不同储存环境下长储后的性能状态,厂家实际储存时引信分为有包装筒密封和无包装筒密封两种储存状态,以下简称密封和非密封。在抽取试验样本时,要注意每个年份点上的抽样样品的生产条件和储存环境基本相同[9-11]。根据产品实际各年份储存数量情况和性能退化分析所需样本量要求,结合GJB166-86《引信制造与验收技术条件》,确定样本量情况如表2所示。
表2 试验样本量情况
Tab.2 Circumstance of the sample quantity for experiment

储存时间/年2345678密封/发8888888非密封/发10101010101010
2.3 试验结果分析
将试验结果取各年份数据的平均值与生产验收原始数据进行对比连线作图。试验共对储存时间为2~8年每年8发密封10发非密封引信开展性能测试,检测了定时器部件的ID,TJ,IG,FX共4项参数和探测器部件的VJ,PW、和不同落速下的炸高H1,H2,H3,H4。
结果显示,密封和非密封状态下各性能参数变化趋势相近;TJ,IG,FX,PW始终维持在相对稳定水平,无明显变化;ID有明显的增大趋势;VJ,H1,H2,H3,H4都有较为明显的减小趋势,其中H1最接近于炸高最低要求。因此,只分析160 m/s落速时炸高H1。ID变化趋势如图2、图3所示;炸高H1变化趋势如图4、图5所示;VJ变化趋势如图6、图7所示。
如图2、图3可知在密封状态时各年份ID增大幅度在1%~6%之间,非密封状态时各年份ID增大幅度在1%~7%之间,虽未发生失效,但都有较明显的退化趋势,因而可以确定ID为性能退化敏感参数。
从图4、图5可以看出,密封状态和非密封状态下长期储存后探测器部件160 m/s落速时炸高H1都呈减小趋势,退化规律明显且距离炸高最低要求较近,因此可以认定炸高H1为性能退化敏感参数。从图6、图7中可以看出,密封与非密封状态检波电压VJ都有比较小的下降趋势,其中密封状态下变化幅度小于5%,非密封状态下变化幅度小于7%,两种状态均满足引信检波电压VJ要求,但性能略有退化。因此可以认定VJ为性能退化敏感参数。
试验结果表明ID,H1和VJ为发火控制部件性能退化敏感参数,且包装筒密封与非密封对其性能退化影响不大。
3 发火控制部件储存寿命预测
利用Matlab软件采用K-S检验法对各性能退化敏感参数分别进行正态分布和威布尔分布的分布假设检验[12]。经检验发现,定时器部件ID和探测器部件的H1,VJ均较好符合威布尔分布,因此采用威布尔分布模型进行寿命预测。
3.1 密封状态下定时器部件储存寿命预测
1) 采用部分数据计算定时器部件ID在各个储存年份的形状参数m与尺度参数η。
采用最佳线性无偏估计BLUE法求出定时器部件ID在各个储存年份的形状参数和尺度参数如表3所示。
表3 定时器ID在各储存年份的形状参数和尺度参数
Tab.3 Shape and Scale Parameters of timer IDunder different storage years

储存年份/年形状参数m尺度参数η018.411 019.020 3221.818 419.612 3323.768 519.862 1424.953 420.152 8522.053 920.485 9626.097 820.742 4729.474 120.931 9834.932 821.211 0
2) 求出定时器部件ID性能退化量分布参数方程系数
根据表3所示,画出ID退化量的形状参数和尺度参数随时间变化的拟合曲线图如8所示。
从表3和图8可以看出,定时器部件ID性能退化量的形状参数、尺度参数基本呈线性关系,因此,选择线性模型,并利用最小二乘法估计参数方程曲线的系数k1,k2,求出形状参数和尺度参数的性能退化轨迹表达式为[9]:
ηy(t)=19.051 86+0.274 4t
(5)
my(t)=17.663 5+1.720 085t
(6)
将式(5)、式(6)代入式(3)中,可以求得有包装筒密封状态下,定时器部件ID性能退化量服从威布尔分布时的可靠度函数为:
(7)
已知引信作用可靠度一般不低于0.9,根据工厂验收指标确定ID失效阈值为指标上限,将失效阈值和可靠度0.9代入式(7)可求得定时器部件基于ID性能退化下的预测寿命为38.824年。
3.2 密封状态下探测器部件储存寿命预测
同理,可求探测器部件基于H1,VJ的形状参数和尺度参数的性能退化轨迹表达式分别为:
ηyH1(t)=0.755 68-0.004 21t
(8)
(9)
ηyVJ(t)=16.1565 1-0.2719 5t
(10)
(11)
将式(8)—式(11)代入式(4)中,可以求得探测器部件H1,VJ性能退化量服从威布尔分布时的可靠度函数分别为:
(12)
(13)
根据工厂验收指标确定探测器部件H1,VJ失效阈值为指标下限,将失效阈值和可靠度0.9分别代入式(12)、式(13)可求得探测器部件基于H1,VJ性能退化下的预测寿命分别为20.707年和22.482年。
同理可求,无包装筒密封状态下定时器部件基于ID性能退化下的预测寿命为37.984年,探测器部件基于H1,VJ性能退化下的预测寿命分别为20.165年和21.786年。定时器部件和探测器部件密封与非密封状态预测寿命如表4所示。
表4 不同部件在不同状态下的预测寿命
Tab.4 Prediction life of different parts under different conditions
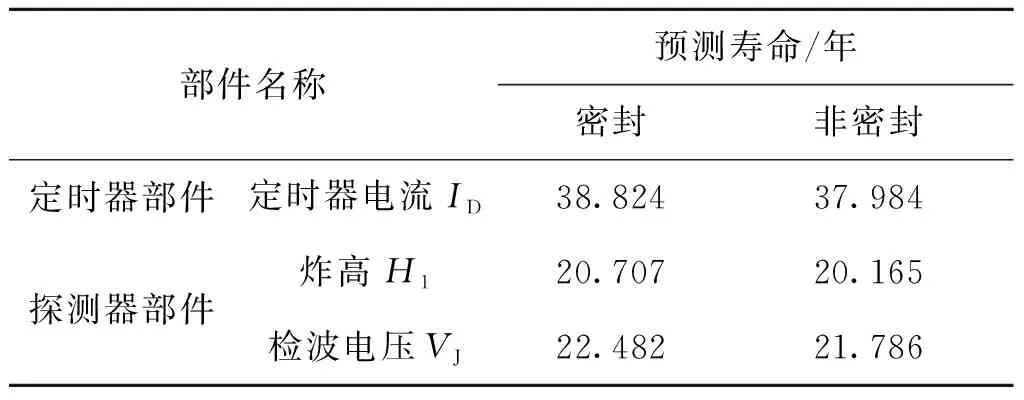
部件名称预测寿命/年密封非密封定时器部件定时器电流ID38.82437.984探测器部件炸高H120.70720.165检波电压VJ22.48221.786
因为电子关键部件最短寿命反映整体寿命,从表4可以看出有包装筒密封、无包装筒密封时该引信发火控制部件储存寿命为探测器部件基于H1性能退化下的储存寿命分别为20.707年、20.165年。通过对比各部件在不同存储状态下的寿命可以发现有无包装筒密封状态下寿命预测结果相差不大,进一步说明引信自身密封的重要性。
4 结论
本文提出了基于储存性能试验的引信发火控制部件寿命预测方法。该方法基于储存性能试验确定了ID,VJ和H1为引信发火控制部件性能退化敏感参数,且引信有无包装筒密封对其性能退化几乎没有影响。并利用Matlab软件采用K-S检验法对性能参数分别进行正态分布和威布尔分布的分布假设检验,确定采用威布尔退化分布模型,利用威布尔退化分布模型求出了ID,H1和VJ对应的储存寿命。预测结果表明,该电容近炸引信发火控制部件在可靠度取值为0.9时,有包装筒密封状态下储存寿命为20.707年,无包装筒密封状态下储存寿命为20.165年。本研究对准确掌握库存同种或同类电容近炸引信质量状况具有重要的参考意义,同时文中的数据分析处理方法也对其他同类型产品的储存寿命预测研究具有一定参考价值。
参考文献:
[1]戴忠亮,李小兵,吴博文,等. 基于改进GM(1,1)模型的引信系统贮存寿命预测方法[J]. 探测与制导学报,2016,38(3):86-89.
[2]郑波,梁兵,方兴桥. 湿热环境下某引信储存寿命评估[J]. 装备环境工程,2011,8(6):1-4.
[3]段亦彬. 基于Matlab软件算法的引信储存寿命预测[J]. 舰船电子工程,2012,32(5):119-120.
[4]张亚,赵河明,董少峰. 无线电引信贮存寿命预测方法研究[J]. 探测与制导学报,2001,23(4):26-29.
[5]孙权,冯静,潘正强. 基于产品性能退化的长寿命产品寿命预测技术[M]. 北京:科学出版社,2015.
[6]魏星. 基于产品性能退化数据的可靠性分析及应用研究[D]. 南京:南京理工大学,2008.
[7]邓爱民. 高可靠长寿命产品可靠性技术研究[D]. 长沙:国防科学技术大学,2006.
[8]吴英伟,齐杏林,郑波,等. 引信典型电子部件长储性能加速退化试验方法[J]. 探测与制导学报,2016,38(4):20-23.
[9]刘传模. 弹药可靠性工程基础[D]. 石家庄:军械工程学院,1996.
[10]郑波,李明,杨宝强,等. 阵地环境下引信贮存可靠性研究[J]. 探测与控制学报,2003,25(3):51-53.
[11]高萌,王金柱,何学广. 基于可靠性统计分析法的制导弹药储存寿命评估[J]. 装备环境工程,2013,10(4):110-113.
[12]张德丰. MATLAB概率与数理统计分析[M]. 北京:机械工业出版社,2010.

