基于几何代数的并联机构自由度自动化分析
杜 鹃 吴洪涛 杨小龙 李 耀
(南京航空航天大学机电学院, 南京 210016)
0 引言
机构自由度是指机构具有确定运动时所必须给定的独立运动参数的数目[1]。自由度分析是机构应用的前提和基础。然而,并联机构作为闭环运动链,一般机构自由度计算采用的G-K公式很难得以正确应用。黄真等[2-3]提出的基于约束螺旋理论的自由度分析方法和修正G-K公式是目前最通用也是最有效的并联机构自由度分析方法,能解决几乎所有并联机构的自由度问题,包括复杂过约束机构,如Bennett机构等[4]。但是基于约束螺旋理论的自由度分析方法在求互易螺旋时需要求解线性方程组,虽然数值求解简单,却很难得到符号或解析表达式。文献[5-6]基于几何代数提出了一种新的自由度分析方法,得到了并联机构自由度的符号表达式。螺旋理论中互易螺旋的求解,几何代数中可以通过对偶的符号表达式来实现,该过程不需要求解线性方程,只涉及几何代数框架下的加法和乘法。不仅如此,由于并联机构动平台的运动空间是各支链运动空间的交集,然而集合并没有交集运算法则,因此基于螺旋理论的自由度分析方法需要首先求解互易螺旋,即支链集合的补集,再通过对补集求并集的运算法则,间接得到动平台运动表达式。但是在几何代数框架下,集合的交集和并集均有直接的运算法则,即交集运算可以通过内积运算法则实现,而并集运算可以通过外积运算法则实现[7]。因此基于几何代数的自由度分析方法能通过对支链运动直接求内积得到并联机构自由度,不需要通过求解补集,即约束螺旋间接得到动平台运动空间,减少自由度求解步骤,使运算更简洁。
但是,无论是基于螺旋理论还是几何代数的并联机构自由度分析方法主要是基于手工求解,难以满足快速分析成千上万机构自由度的需求。机构的构型创新是机械装备原始性创新的重要内容,构型综合是构型创新的有效手段[8-9]。随着计算机技术的发展,建立基于计算机技术的数字化构型综合理论,进而实现机构概念创新设计的自动化、可视化、网络化和智能化是机构学研究的趋势。而并联机构自由度数字化、程序化、自动化分析是并联机构数字化结构综合的基础。曹文熬[10]基于螺旋理论提出了一种空间并联机构自由度自动化分析算法,并成功应用于数字化结构综合中。该方法通过螺旋之间的垂直、平行等几何关系,在已知支链第一个运动螺旋的情况下,自动求解支链的所有螺旋,从而实现并联机构自由度自动化分析。文献[5-6]基于几何代数的自由度分析方法也可利用类似过程,得到自动化分析算法。但是这些方法都无法得到符号表达式,因为通过几何关系如垂直、平行等求解相邻螺旋仍然是一个线性方程求解过程。事实上,任意一个螺旋都可通过另一螺旋的旋转和平移运动得到,而几何代数的另一优势就是能符号描述几何元素的刚体运动。但是,文献[5-6]所用的R(6,0)几何代数空间,由于不是零向量空间,因而没有平移变换的符号表达式[7],从而无法用符号描述运动螺旋间的几何关系,进而无法通过符号表达式实现并联机构自由度的自动化分析。
R(3,3)几何代数空间[11-12]与R(6,0)几何代数空间同为六维几何代数空间。R(3,3)不仅具有R(6,0)的优势,还存在螺旋的符号表达式,从而可实现符号描述并联机构自由度,同时还能够符号描述平移和旋转运动。本文基于R(3,3)几何代数空间提出一种并联机构自由度自动化分析算法。
1 R(3,3)几何代数
1.1 几何代数
几何代数又称为Clifford代数,由CLIFFORD[13]在1876年首次提出,随后HESTENES[14]将Clifford代数进行几何意义上的解释,使之更加完善。几何代数是一种完全不同于传统代数的计算框架,已被广泛应用到机器视觉[15-16]、计算机图形学[17]和机器人学[18]等领域。
n维几何代数空间表示该空间由n个正交基e1,e2,…,en组成。然而与欧几里得空间不同的是,几何代数空间中基的长度可以为正,可以为负,也可以为零。一般为
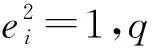
几何积是几何代数特有的乘积运算符。向量a和向量b的几何积定义为
ab=a·b+a∧b
其中a·b表示向量a和向量b的内积,a∧b表示向量a和向量b的外积。关于内积和外积,有以下运算法则
eiei=±1,0ei∧ei=0
eiej=0ei∧ej=-ej∧ei(i≠j)
同时,在几何代数空间中,向量a的长度可以用内积描述为
‖a‖2=aa
(1)
通常,用eijk简化表示ei∧ej∧ek。由n个单位基组成的伪标量定义为
I=e1∧e2∧…∧en=e12…n
向量A的对偶为A的正交补,定义为
D=AI-1
其中I-1=en…21
式中I-1——伪标量I的逆
更多关于几何代数的定义和定理见文献[19]。
1.2 R(6,0)几何代数空间
文献[5-6]基于R(6,0)几何代数空间提出了一种新的并联机构自由度分析算法。R(6,0)是一个六维几何代数空间。设e1、e2、e3、e4、e5和e6是R6的一组单位正交基,其中
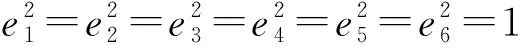
则螺旋理论中的螺旋
$=(v1,v2,v3;b1,b2,b3)
在R(6,0)几何代数空间中可写成
l=v1e1+v2e2+v3e3+b1e4+b2e5+b3e6
由式(1)可知,l的长度为
在几何代数中,无论是旋转算子还是平移算子,都具有保长性,即向量经过平移或旋转后,自身长度保持不变。然而在R(6,0)几何代数空间中,若t为平移向量,则
‖l+t‖2=(l+t)(l+t)=
‖l‖2+‖t‖2+2lt≠‖l‖2
因此,R(6,0)几何代数空间中没有平移算子。同时,几何代数空间中向量具有平移算子的前提是该向量的长度为零,称为零向量[7]。例如,共形几何存在平移算子是由于共形几何中的向量是零向量,即

因而,为了将平移算子和旋转算子应用于螺旋,从而实现并联机构自由度自动化分析的符号描述,需要寻找一个新的空间,该空间需要既能符号描述螺旋,还能符号描述对螺旋进行平移和旋转的刚体变换。
1.3 R(3,3)几何代数空间
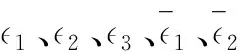
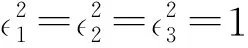
但是这一组正交基向量主要用于计算,不用于几何元素的描述。为了描述螺旋,定义以下一组基向量,称为Witt基[20]。令
计算可知,该组基向量为零向量,因为
同时该组基向量并不是两两正交,其中
e1e4=e2e5=e3e6=-1
那么,螺旋理论中的螺旋
$=(v1,v2,v3;b1,b2,b3)
在R(3,3)几何代数空间中可写成
l=v1e1+v2e2+v3e3+b1e4+b2e5+b3e6
这里,l也为零向量。
R(3,3)几何代数空间不仅能符号描述螺旋,还能符号描述刚体运动。单位矢量为t=(t1,t2,t3),平移距离为a的平移算子在R(3,3)几何代数空间为
(2)
旋转描述较之于平移描述略微复杂。绕过原点u=(u1,u2,u3)轴,旋转角度为θ的旋转算子在R(3,3)几何代数空间为
R=1+sinθB+(1-cosθ)B2
(3)
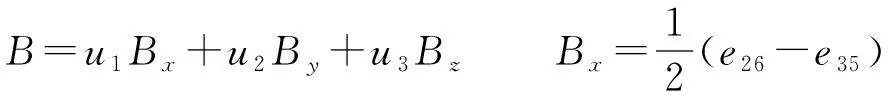
对于R(3,3)模型中的任意螺旋,其刚体运动都可描述成
(4)
(5)
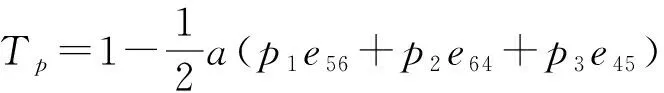
不仅如此,若螺旋li+1为螺旋li绕u轴旋转θ后沿t轴平移a所得螺旋,则R(3,3)形式可写成
(6)
因此,任意一个螺旋都可通过另一螺旋的刚体变换得到。例如螺旋l2=e2+2e4+e6可以由螺旋l1=e1+e6沿z轴旋转90°后再沿z轴平移2个单位得到,即
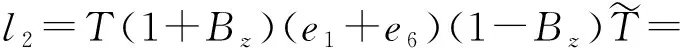
基于螺旋之间刚体运动符号表达式,可以实现并联机构在已知分支第一个运动副螺旋的情况下,自动求解该分支所有螺旋系,进而实现并联机构自由度的自动化分析算法。
2 基于几何代数的支链运动空间自动求解
2.1 构型描述
为实现并联机构自由度自动化分析,首先需要建立便于计算机程序识别的字符串构型描述,这一字符串描述包含机构自由度分析所需的所有必要信息。螺旋的相关性能通过初等变换的方式来判定,但从几何角度判定更加简洁[21]。基于几何关系的并联机构字符串描述更加直接。使用文献[10]中的字符串定义方法。表1为相邻轴线之间的6种几何关系以及符号描述,其中垂直为两螺旋异面情况,正交为两螺旋共面情况。

表1 相邻轴线几何关系的描述Tab.1 Representation of geometric relationships between adjacent axes
机构中常见的单自由度运动副为转动副(R)和移动副(P)。复合副如球副(S)、虎克铰(U)和圆柱副(C)都能看作是单自由度运动副的组合。一般地,将分支看作只由单自由度运动副组成,并将单自由度运动副从静平台到动平台依次编号为1,2,…,t。若一个移动副和一个转动副正交,那么字符串根据表1可描述为P+R。球铰(S)可描述为R+R*R,其中*表示正交于前两个轴线所成平面。并联机构3-RPS有3个相同的RPS分支运动链,其中R与定平台相连接;P为驱动关节,与R正交;S与动平台相连接。因此每个分支运动链的计算机构型字符串可以描述为R+P|R+R*R。
通过几何关系分析可知,任意轴线都可由另一已知轴线通过平移和旋转的刚体变换得到。例如若一个螺旋平行于另一个螺旋,那么该螺旋可以由另一个螺旋平移得到。利用R(3,3)几何代数空间不仅能符号描述螺旋,还能符号描述螺旋的刚体运动的优势,基于螺旋间的几何关系,建立由已知螺旋求解未知螺旋的符号表达式,可以实现并联机构在已知分支第一个运动副螺旋的情况下,自动求解该分支所有螺旋系,进而实现并联机构自由度的自动化算法。
2.2 分支螺旋系自动求解算法
不失一般性,假定第i个运动轴线在R(3,3)几何代数空间中的表达式为
li=u1e1+u2e2+u3e3+b1e4+b2e5+b3e6
那么该运动轴线的方向矢量为u=(u1,u2,u3)。令u⊥=v=(v1,v2,v3),由于vu=0,v2=1,因此垂直矢量v有一个自由度。根据不同的几何关系,可写出第i+1个运动轴线的符号表达式li+1。第i+1个运动副与第i运动副有如下关系:
(1)共轴,则li+1相当于li沿u轴平移a的刚体变换后所得。
(2)平行,则li+1相当于li沿t=(t1,t2,t3)轴平移a的刚体变换后所得。
(3)正交,则li+1相当于li绕过交点p=(p1,p2,p3)、方向为v⊥的轴旋转90°的刚体变换后所得。
(4)相交,则li+1相当于li绕过交点p=(p1,p2,p3)、方向为w=(w1,w2,w3)的轴旋转θ的刚体变换后所得。
(5)垂直,则li+1相当于li绕过垂足p=(p1,p2,p3)、方向为v⊥的轴旋转90°,然后沿v⊥平移a的刚体变换后所得。
(6)异面,则li+1相当于li方向为w=(w1,w2,w3)的轴旋转θ,然后沿t=(t1,t2,t3)平移a的刚体变换后所得。
利用1.3节中R(3,3)几何代数空间的刚体运动符号描述,得到根据已知螺旋求解未知螺旋的符号表达式,见表2。
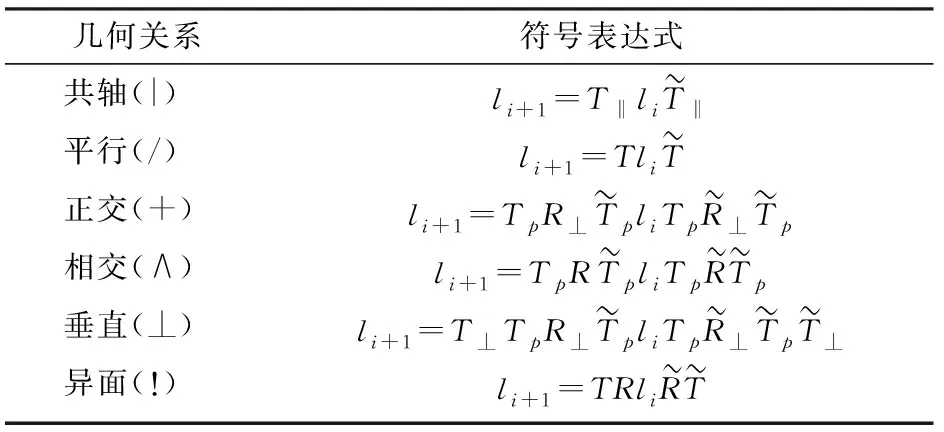
表2 未知螺旋求解符号表达式Tab.2 Symbolic expressions of unknown twists
表中
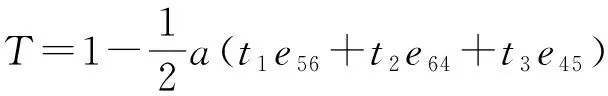
在自动求得分支所有运动轴线li的符号表达式后,再根据运动副类型得到该分支的运动螺旋。不失一般性,若运动轴线表达式为
l=u1e1+u2e2+u3e3+b1e4+b2e5+b3e6
那么如果运动副类型为转动副(R),运动螺旋S=l;如果运动副类型为平移副(P),运动螺旋S=F(l)=u1e4+u2e5+u3e6。
通过以上分析,以字符串描述为基础,结合运动副轴线符号表达式,可以实现分支运动螺旋的计算机程序化、自动化求解,算法流程图如图1所示。
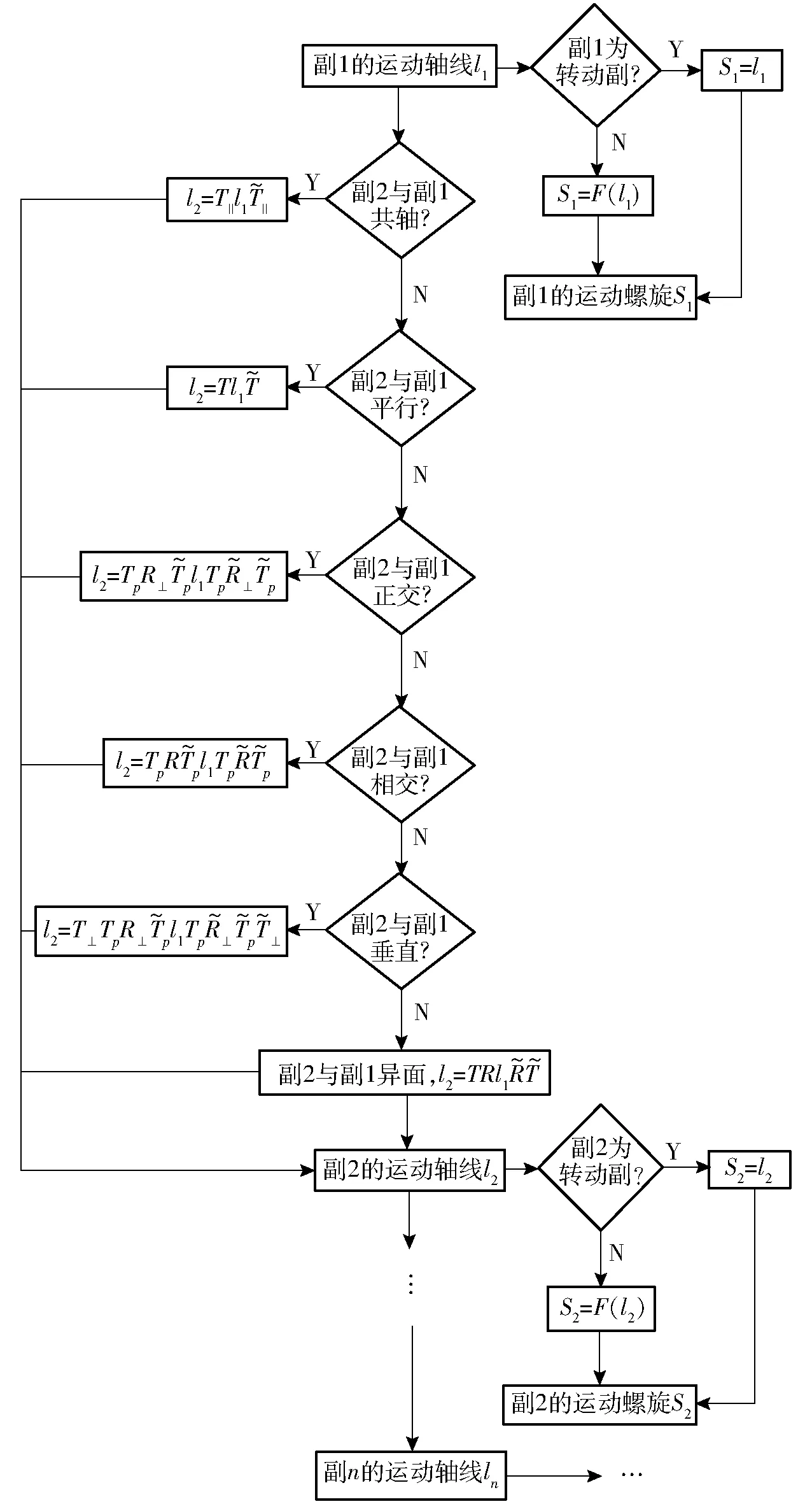
图1 并联机构支链运动螺旋系自动化算法流程Fig.1 Flow chart of automatic motion analysis of limbs using geometry algebra
3 基于几何代数的并联机构自由度自动化分析
不同于螺旋理论没有直接求解集合交集的运算法则,在几何代数框架下,集合的交集和并集可以通过内积和外积运算法则直接得到。因此,基于几何代数的并联机构自由度分析不需要通过求解约束螺旋间接得到动平台运动空间,从而简化自由度求解步骤。因此在得到并联机构支链自动化求解符号表达后,可以通过几何代数符号描述并联机构自由度。
根据第2节中的讨论,R(3,3)几何代数空间不仅能描述并联机构的螺旋运动,还能对螺旋运动进行平移和旋转的刚体变换的符号描述。同时R(3,3)几何代数与R(6,0)几何代数一样,均为六维几何代数空间,具有相同的旋量表达式;并且2个空间有着相同的内积和对偶表达式。因而在自动求解支链螺旋符号表达式后,R(3,3)几何代数和R(6,0)几何代数有着相同的并联机构自由度符号表达式。
综上所述,并联机构自由度自动化算法分为以下几个步骤:
(1)利用螺旋之间的几何关系,基于R(3,3)几何代数刚体运动符号表达式,自动写出第i个分支运动链上第j个运动副在几何代数框架下螺旋表达式Smij。
(2)利用几何代数能通过外积运算法则求解集合并集的优势,计算出第i个分支运动链末端的许动子空间
Smi=Smi1∪Smi2∪…∪Smij∪…∪Smik=
Smi1∧Smi2∧…∧Smij∧…∧Smik
其中∧为几何代数外积符号。若运动副线性相关,即运动副运动空间有交集,表示并联机构具有冗余驱动力,此时需要对冗余驱动力在几何代数空间中进行判别和剔除。
(3)利用几何代数能通过内积和对偶运算法则求解集合交集的优势计算出动平台许动子空间
Sm=Sm1∩Sm2∩…∩Smi∩…∩Smn
其中,当2个分支运动链末端的许动子空间的并集为I6时,交集可写为
其中·为几何代数内积符号。当两个分支运动链末端的许动子空间的并集不等于I6时,需要使用两者的并集替代I6。
所求的动平台许动子空间符号表达式基的维度即为并联机构自由度个数,基的外积组成即为并联机构自由度运动方向。例如,若动平台许动子空间S=e1∧e2∧e6,则表示该并联机构的自由度为3,运动方向分别是沿x轴和y轴的旋转,以及绕z轴的平移。并联机构自由度自动化算法流程图见图2。
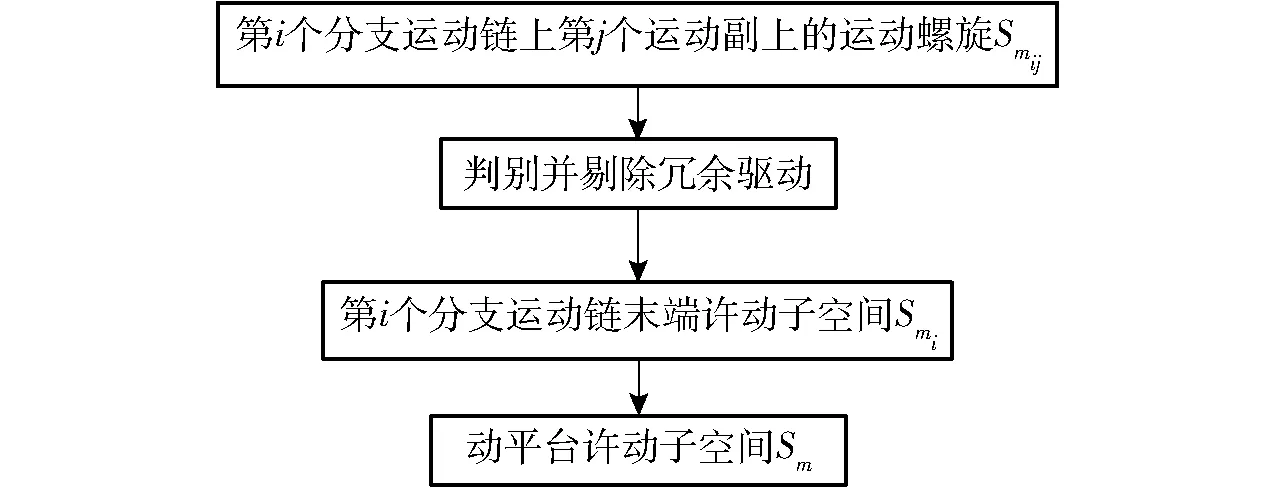
图2 并联机构自由度自动化算法流程Fig.2 Flow chart of mobility analysis using geometry algebra
4 基于几何代数的并联机构自由度自动化分析算法验证
4.1 算法可行性一般性验证
为了对本文提出的并联机构自由度自动化求解算法的正确性进行一般性验证,需对该算法进行可行性分析:
(1)并联机构任意运动副的螺旋均可在R(3,3)几何代数空间进行描述。
(2)任意螺旋均可通过已知螺旋的刚体运动得到。
(3)在已知并联机构支链第1个运动副螺旋以及支链各运动副之间几何关系的情况下,该支链所有螺旋系能够符号描述,并且能利用符号描述进行自动化求解。
(4)在自动求得并联机构所有螺旋系的几何代数表达式后,可以通几何代数框架下的运算法则得到并联机构的自由度和运动方向的符号表达式,进而实现并联机构自由度自动化算法。
证明如下:
(1)由文献[12]可知,R(3,3)几何代数中6个一维向量对应旋量中的6个参数,即e1、e2、e3表示旋转,e4、e5、e6表示移动;因此旋量与R(3,3)空间存在一一对应的映射关系,并联机构任意运动副的螺旋均可在R(3,3)空间中进行描述。
(2)任意两旋量之间只存在6种几何关系,即共轴、平行、正交、相交、垂直、异面,而这6种几何关系均可通过平移和旋转的刚体运动来描述,例如某螺旋与一已知螺旋异面,其中两螺旋距离为d,夹角为θ,那么该螺旋可以通过已知螺旋绕公垂线旋转θ后再沿着公垂线平移d后得到。
(3)在文献[11]中已证明,通过R(3,3)描述的旋量存在平移和旋转的刚体运动符号表达式。因此在R(3,3)几何代数空间中,已知并联机构支链第1个运动副螺旋以及支链各运动副之间几何关系的情况下,可以通过刚体运动符号表达式描述该支链所有螺旋,从而实现并联机构螺旋系的自动化计算。
(4)在自动求得并联机构所有螺旋系的几何代数表达式后,可以通过几何代数的并集和交集运算法则求得并联机构自由度和运动情况,这在文献[5-6]中已得到证明。这是因为并联机构各支链的运动是该支链所有螺旋的并集,同时并联机构动平台的运动是各支链运动的交集;而在几何代数框架下可以通过外积运算法则符号描述螺旋并集,内积运算法则符号描述螺旋交集,从而得到并联机构自由度的符号表达式,进而实现并联机构自由度自动化算法。
在并联机构自由度自动化求解算法包含的4个步骤均证明可行的情况下可证明该算法可行。
4.2 算法可行性例子验证
基于gaigen 2.5几何代数分析软件包[22],生成满足R(3,3)几何代数运算法则的源文件,基于C++平台实现并联机构自由度自动化分析算法,从而验证该算法的正确性、有效性。
以3-RPS并联机构为例验证并联机构自由度自动化分析算法。3-RPS有3个相同的RPS分支运动链,如图3所示,每个运动分支的计算机构型字符串可以描述为R+P|R+R*R。

图3 3-RPS并联机构机构简图Fig.3 Schematic diagram of 3-RPS parallel mechanism
首先对第1个分支进行自动求解。不失一般性,令该分支的第1个运动副过点B1=(B1x,B1y,B1z),运动轴线为
l11=u111e1+u112e2+u113e3+b111e4+
b112e5+b113e6
由计算机构型字符串可知,该运动副为转动副,因此第1个运动副的运动螺旋为S11=l11。
第2个运动螺旋和第1个运动螺旋正交,交点为p1,那么由表2可知
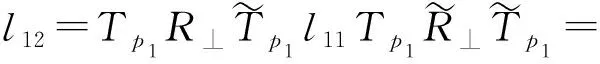
该运动副为移动副,因此运动螺旋为
S12=F(l12)=u121e4+u122e5+u123e6
同理可知,第3个运动螺旋和第2个运动螺旋共轴,运动螺旋为
第4个运动副与第3个运动副正交,交点为p2,运动螺旋为
第5个运动副与第3个和第4个运动副正交,交点为p2,运动螺旋为
那么,第1个分支运动链末端的许动子空间为
S1=S11∪S12∪S13∪S14∪S15=
S11∧S12∧S13∧S14∧S15
同理可求得第2、3个分支运动链末端的许动子空间S2、S3。
因而3-RPS并联机构的自由度符号表达式为
S=((S1I-1)S2I-1)S3=
a1e123+a2e124+a3e125+a4e126+a5e134+
a6e135+a7e136+a8e145+a9e146+a10e156+
a11e234+a12e235+a13e236+a14e245+a15e246+
a16e256+a17e345+a18e346+a19e356+a20e456
其中
eijk=ei∧ej∧ek
式中ai——标量系数
由S的符号表达式可知,动平台许动子空间为一个3维基(3-blade),因此3-RPS并联机构的自由度为3。
即使相同的并联机构在不同位形下自由度和运动情况也可能不同。基于几何代数的并联机构的自由度自动化算法不仅能求解某种机构在通用参数下的自由度,还能求解在已知连杆参数尺寸和位置下的自由度和运动情况。以3-URU并联机构为例,对本文提出方法进行验证。
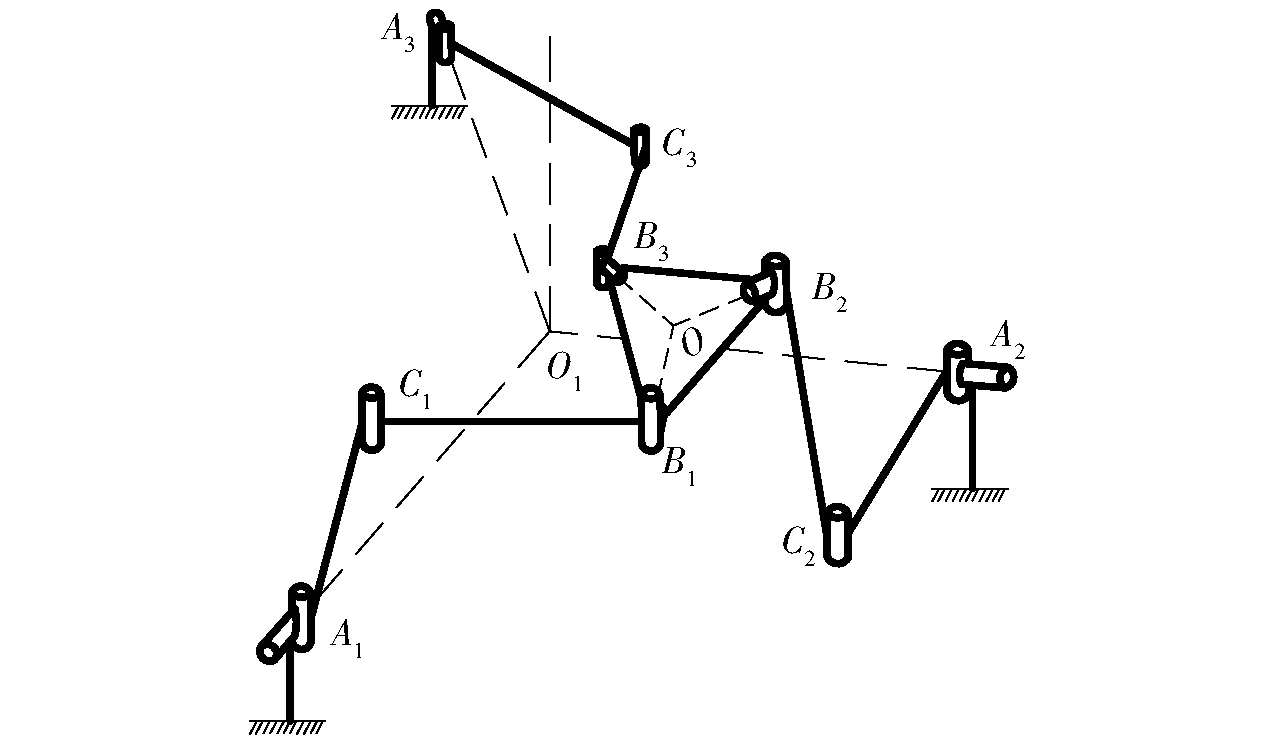
图4 3-URU并联机构处于平面运动位形机构简图Fig.4 Schematic diagram of 3-URU parallel mechanism in planar mode
如图4所示,若3-URU并联机构的动平台B1B2B3为外接圆半径为3的等边三角形,外接圆圆心为O;3个基座A1、A2、A3分布在外接圆半径为5的等边三角形的3个顶点上,外接圆圆心为O1;杆长AiCi为4,杆长BiCi为3,i=1,2,3;每个运动分支的计算机构型字符串描述为R⊥R|R|R⊥R。
由文献[21]可知,若动平台B1B2B3与3个基座A1A2A3共面,且2个外接圆圆心O、O1不重合,如图4所示,那么该并联机构的自由度为3,分别为沿x、y的平移和绕z轴的旋转。
若第1个基座的第1个运动副过点(5,0,0),方向为(1,0,0),运动轴线为
S11=l11=e1
第2个运动螺旋和第1个运动螺旋正交,交点为(5,0,0),那么由表2可知
同理可知,第3个运动螺旋和第2个运动螺旋平行且过点(4.47,3.96,0),运动螺旋为
第4个运动副与第3个运动副平行且过点(3,0,0),运动螺旋为
第5个运动副与第4个运动副正交,交点为(3,0,0),运动螺旋为

那么,第1个分支运动链末端的许动子空间为
S1=S11∧S12∧S13∧S14∧S15=9e12345+9e13456
同理可求得第2、3个分支运动链末端的许动子空间分别为
S2=10.31e12345+5.16e13456-8.93e23456
S3=10.06e12345
因而3-URU并联机构的自由度符号表达式为
S=((S1I-1)S2I-1)S3=a(e3∧e4∧e5)
式中a——标量系数
由S的符号表达式可知,在该运动空间情况下,3-URU并联机构的自由度为3,分别为沿x、y轴的平移和绕z轴的旋转。
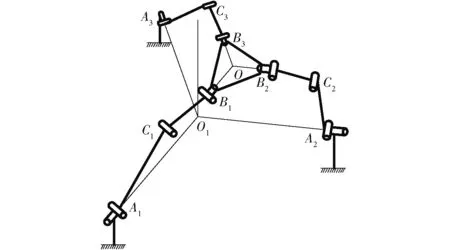
图5 3-URU并联机构处于平移运动位形机构简图Fig.5 Schematic diagram of 3-URU parallel mechanismin translation mode
同理可求,若动平台B1B2B3与3个基座A1A2A3平行但不共面,且2个外接圆圆心O、O1不重合,如图5所示,则并联机构的自由度符号表达式为
S=((S1I-1)S2I-1)S3=a(e4∧e5∧e6)
3-URU并联机构的自由度为3,分别为沿x、y、z轴的平移。
若动平台B1B2B3与3个基座A1A2A3不平行,但2个外接圆圆心O、O1重合,如图6所示,那么根据并联机构的自由度符号表达式可知,3-URU并联机构的自由度为3,分别为绕x、y、z轴的旋转。
基于本文提出的算法对3-URU并联机构在不同位形下自由度分析所得结论与文献[23]中的结论相同,从而证明本文算法可行。
5 结论
(1)R(3,3)几何代数空间不仅与R(6,0)空间一样能够描述运动螺旋,得到并联机构自由度的符号表达式,而且R(3,3)空间具有平移、旋转刚体运动的符号表达式,从而能够实现并联机构自由度自动化算法。
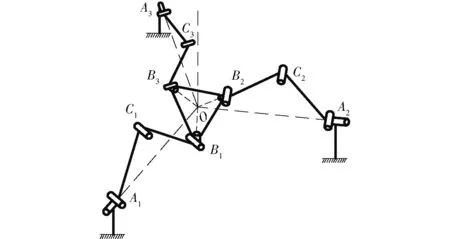
图6 3-URU并联机构处于旋转运动位形机构简图Fig.6 Schematic diagram of 3-URU parallel mechanism in orientation mode
(2)提出的算法不仅具有基于几何代数算法的优点,即不需要求解线性方程组,能给出自动化求解的符号表达式,算法简单,效率高,同时由于几何代数具有集合求交的运算法则,因而在自由度分析过程中可以直接通过各支链求交运算得到自由度运动空间,不需要通过约束螺旋间接得到并联机构自由度。并且由于即使并联机构字符串构型描述相同,机构也可能会有不同的自由度,本文提出的算法不仅能求解机构在通用参数情况下的自由度,还能求解机构在特定参数和位置情况下的自由度和运动情况。
1 邹慧君, 楼鸿棣. 高等机械原理[M]. 北京:高等教育出版社, 1990.
2 黄真, 孔令富, 方跃法. 并联机器人机构学理论及控制[M]. 北京:机械工业出版社, 1997.
3 黄真, 刘婧芳, 曾达幸. 基于约束螺旋理论的机构自由度分析的普遍方法[J]. 中国科学, 2009, 39(1):84-93.
HUANG Zhen, LIU Jingfang, ZENG Daxing. General method formobility analysis of mechanisms based on constrained screw theory[J]. Science in China Press, 2009, 39(1):84-93. (in Chinese)
4 黄真, 夏平, 丁华锋. Bennett机构自由度的螺旋分析[J]. 燕山大学学报, 2004, 28(3):189-191.
HUANG Zhen, XIA Ping, DING Huafeng. Mobility analysis of Bennett based on constrained screw theory[J]. Journal of Yanshan University, 2004, 28(3):189-191. (in Chinese)
5 LI Q, CHAI X. Mobility analysis of limited degrees of freedom parallel mechanisms in the framework of geometric algebra[J].Journal of Mechanisms and Robotics, 2016,8(4):041005.
6 CHAI X, LI Q. Mobility analysis of two limited-DOF parallel mechanisms using geometric algebra[C]∥International Conference on Intelligent Robotics and Applications.Cham. Springer, 2016: 13-22.
7 DORST L, FONTIJNE D, MANN S.Geometric algebra for computer science: an object-oriented approach to geometry[M]. Morgan Kaufmann Publishers Inc., 2009.
8 曹毅, 秦友蕾, 陈海,等. 基于GF集理论的五自由度混联机器人构型综合[J/OL]. 农业机械学报, 2015, 46(11):392-398.http:∥www.jcsam.org/ch/reader/view_abstract.aspx?file_no=20151153&flag=1&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.11.053.
CAO Yi,QIN Youlei, CHEN Hai, et al. Structural synthesis of 5-DOF hybrid mechanisms based on GF set[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(11):392-398. (in Chinese)
9 朱小蓉, 宋月月, 沈惠平,等. 基于POC方法的少自由度无过约束并联机构构型综合[J/OL]. 农业机械学报, 2016, 47(8):370-377.http:∥www.jcsam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160849&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.08.049.
ZHU Xiaorong, SONG Yueyue, SHEN Huiping, et al. Structural synthesis based on POC set for lower-mobility non-overconstrained parallel mechanisms[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8):370-377. (in Chinese)
10 曹文熬. 空间多环耦合机构数字化构型综合理论[D]. 秦皇岛:燕山大学, 2014.
CAO Wenao. Digital type synthesis theory of spatial multiloop coupling mechanism[D]. Qinhuangdao:Yanshan University,2014. (in Chinese)
11 DORST L. 3D oriented projective geometry through versors of R(3,3)[J]. Advances in Applied Clifford Algebras, 2016, 26(4):1-36.
12 LI H, ZHANG L. Line geometry in terms of the null geometric algebra over R(3,3),and application to the inverse singularity analysis of generalized Stewart platforms[M]∥LASENBY J. Guide to geometric algebra in practice. Springer London, 2011:207-221.
13 CLIFFORD W. Elements of dynamic: an introduction to the study of motion and rest in solid and fluid bodies[M]. MacMillan and Company, 1878.
14 HESTENES D. New foundations for classical mechanics[M]. Springer Science and Business Media, 2012.
15 SOMMER G. Applications of geometric algebra in robot vision[J].Computer Algebra and Geometric Algebra with Applications, 2005: 258-277.
16 SOMMER G.Geometric computing with Clifford algebras: the oretical foundations and applications in computer vision and robotics[M]. Springer Science and Business Media, 2013.
17 HILDENBRAND D. Geometric computing in computer graphics using conformal geometric algebra[J]. Computers and Graphics,2005, 29(5): 795-803.
18 ARISTIDOU A. Inverse kinematics solutions using conformal geometric algebra[M]∥LASENBY J. Guide to geometric algebra in practice. Springer London, 2011:47-62.
19 DORAN C, LASENBY A.Geometric algebra for physicists[M]. Cambridge University Press, 2003.
20 DU J, GOLDMAN R, MANN S. Modeling 3D geometry in the Clifford algebra R(4,4)[J].Advances in Applied Clifford Algebras,2017: 1-24.
21 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京:高等教育出版社, 2006.
22 FONTIJNE D. Gaigen 2: a geometric algebra implementation generator[C]∥Proceedings of the 5th International Conference on Generative Programming and Component Engineering. ACM, 2006: 141-150.
23 ZLATANOV D, BONEV I, GOSSELIN C. Constraint singularities as C-space singularities[J].Advances in Robot Kinematics, 2002:183-192.

