无寄生运动非对称空间2T1R并联机构设计与运动学分析
邓嘉鸣 许 可 赵迎春 沈惠平 张 震 杨廷力
(常州大学现代机构学研究中心, 常州 213016)
0 引言
三自由度的三维纯平移和三维纯转动并联机构已得到了较多的研究与应用[1-4],而具有转动和移动混合输出的三自由度并联机构同样具有较好的研究价值。有关一平移两转动(1T2R)并联机构的研究,已有3-PRRU并联机构[5],Exechon机器人[6-7]中的2-UPR-SPR并联机构,Tricept和TriVariant机器人[8-10]中的3-UPS-UP和2-UPS-UP并联机构。王飞博等[11]运用基于螺旋理论的运动/力传递性能指标对3-PRRU、2-PRU-PRRU和2-PRS-PRRU 3种1T2R并联机构进行构型优选。汪满新等[12]运用虚拟链法对1T2R型并联机构进行型综合,得到多种含冗余驱动/过约束的新构型。HUNT[13]提出一种动平台包含寄生运动的3-PRS并联机构,JOSHI等[14]对此机构进行了奇异分析。
目前,对两平移一转动(2T1R)机构研究相对较少,但这类机构可用作空间抓放定位操作、娱乐设备、调姿装备等,例:KONG等[15]、杨宁等[16]分别基于螺旋理论对2T1R型并联机构的结构综合进行了研究;REFAAT等[17]根据位移李群理论对三自由度混合运动并联机构进行型综合研究;张彦斌等[18]根据线性变换理论,对无奇异完全各向同性2T1R型空间并联机构进行了结构综合,杨廷力等[19-21]基于单开链单元理论对2T1R型并联机构进行了型综合,得到多种含有平面闭回路结构的新型机构。
寄生运动,即伴随运动、派生运动、衍生运动,是指并联机构动平台的运动输出量数目大于机构的自由度(或驱动副数目)的那一部分运动,它是由独立运动派生(或衍生)的。一般情况下不希望产生寄生运动,因为对需要精确输出运动的机构来说,其运动规划与控制比较复杂;但文献[22-23]却逆向思考,提出了“少输入-多输出并联机构”的研究对象、设计理论和方法,设计的系列含寄生运动的并联机构,并应用于筛分[24-25]、康复[26-27]混合、娱乐等不需要精确运动的装备上。
本文研究无寄生运动的2T1R机构。根据基于方位特征(POC)的并联机构设计理论与方法[19-21],设计一种能实现空间两平移一转动(2T1R)的并联机构(RPa‖3R)-R+RSS;对该机构进行拓扑特征、位置正反解求解、动平台工作空间及其转动能力、奇异位形,以及速度与加速度的分析。
1 2T1R并联机构的设计及拓扑分析
1.1 机构设计
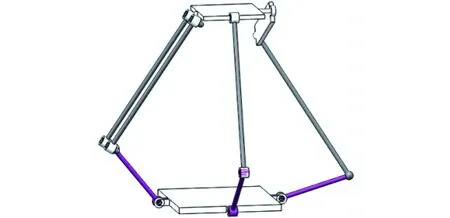
根据基于方位特征(POC)方程的并联机构拓扑结构设计理论和方法[20-21],本文提出的2T1R并联机构如图1所示,静平台0与动平台1用一条无约束支链(SOC)和一条混合支链HSOC联接。
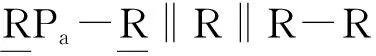
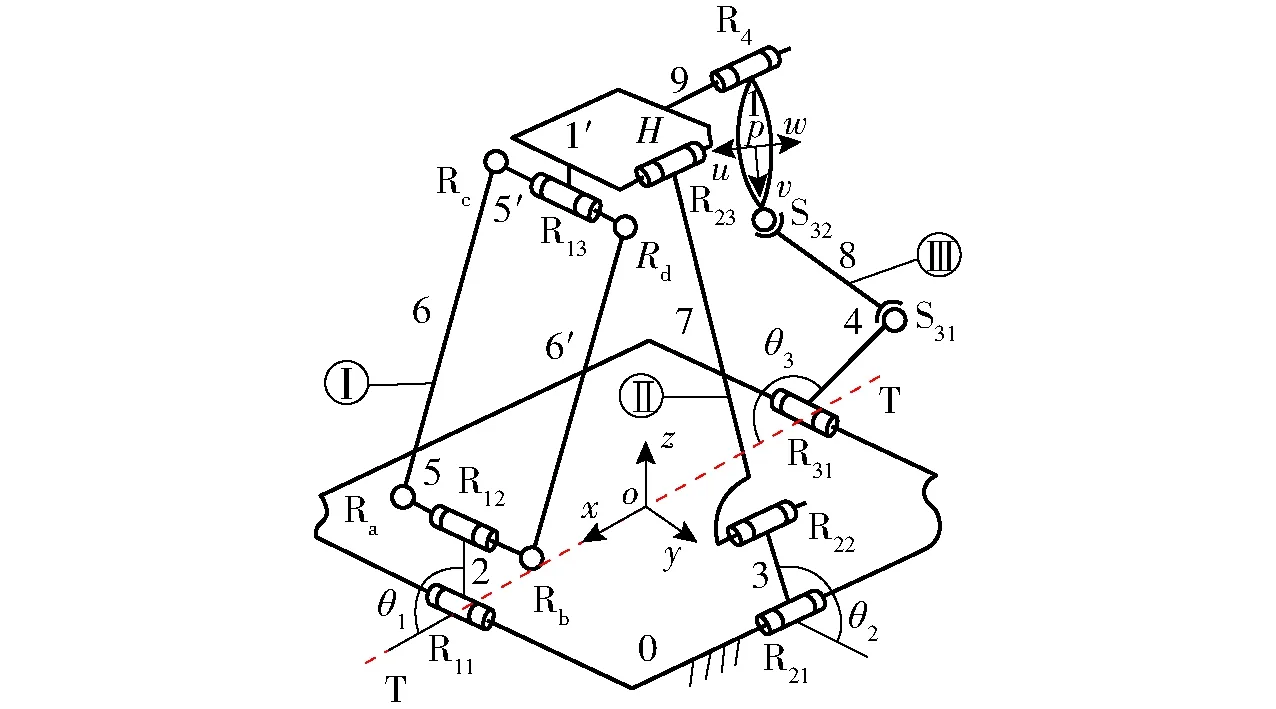
图1 非对称零耦合度(RPa‖3R)-R+RSS机构Fig.1 Asymmetric and zero coupling degree mechanism (RPa‖3R)-R+RSS
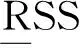
因此,整个并联机构记为(RPa‖3R)-R+RSS。
1.2 机构拓扑特性分析
1.2.1机构的POC计算
1.2.1.1并联机构的POC方程[22]为
(1)
(2)
式中MPa——机构动平台的POC集
Mbi——第i条支链末端的POC集
Msj——支链中第j个子SOC的POC集
1.2.1.2动平台的POC集
(1)机构的拓扑结构
组成子并联机构的Ⅰ、Ⅱ支链的拓扑结构分别为
SOC1{-R11‖R12(-P4R-)‖R13-}
SOC2{-R21‖R22‖R23-}
静平台0上R11与R21为垂直布置,即R21⊥R11;R31可任意布置,取R31‖R11。选定动平台1上的任一点为基点O′。
(2)确定混合支链HSOC末端构件的POC集
设H为子并联机构子平台上的任一点,则子平台产生的POC集为
表明子平台1′仅产生oyz平面内的二维平移。
而混合支链未端产生的POC集为
(3)确定动平台POC集
因无约束支链RSS的POC集为3T3R,因此,动平台1的POC集为
表明动平台1仅产生在垂直于R23轴线平面(即oyz平面)内的二维平移,以及绕R4轴线的转动,而没有其他的寄生运动或伴随运动。
1.2.2机构自由度计算
1.2.2.1并联机构全周性自由度公式[24]为
(3)
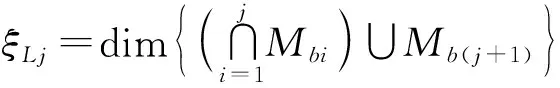
(4)
v=m-n+1
式中F——机构自由度
fi——第i个运动副的自由度
m——运动副数n——构件数
v——独立回路数
ξLj——第j个回路的独立位移方程数
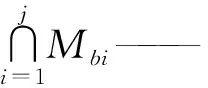
Mb(j+1)——j+1条支链末端构件的POC集
1.2.2.2机构的DOF计算
(1)确定独立回路的位移方程数
该机构可分解为2个独立回路,其组成分别为
HSOC1{-R11‖R12(-P4R-)‖R13-
R23‖R22‖R21-}
SOC3{-R4-S32-S31-R31-}
它们的独立位移方程数计算如下:
①支链Ⅰ、Ⅱ组成的子并联机构为第1个独立回路,可得
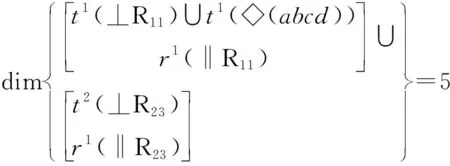
该子并联机构的POC集为
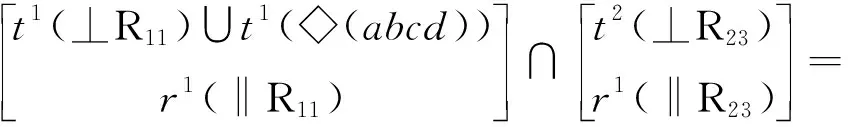
可得该子并联机构的自由度为
此即表明,子平台1′在oyz平面内产生的二维平移,仅由该回路内的驱动副R11、R21决定,因此,该机构具有部分输入-输出运动解耦性。
②上述子并联机构与单开链SOC3组成第2个回路,可得
(2)确定该并联机构的自由度
因此,该机构的自由度为3,可取静平台上的R11、R21、R31为驱动副。
注:若将该机构视为仅由产生2T1R的等效混合支链和一条简单支链组成的一个独立回路,即
SOC{-P*-P*-R4-S32-S31-R31-}
则其独立位移方程数为
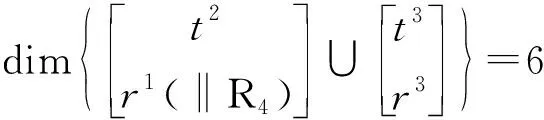
则机构自由度为
显然,自由度计算时,如将含回路的子并联机构用等效支链替代,则计算过程比较方便。
1.2.3机构耦合度κ计算
(1)耦合度定义
由基于序单开链(SOC)单元的机构组成原理[22]知,任意机构可分解为若干个基本运动链(Basic kinematics chain,BKC);而独立回路为v的BKC可进一步分解为v个单开链SOC(Δj)(j=1,2,…,v),而第j个单开链(SOCj)的约束度定义为
(5)
其中
式中mj——第j个SOCj的运动副数
Ij——第j个SOCj的驱动副数
Δj有正、零、负3种形式,但须满足∑Δj=0。
因此,BKC的耦合度к定义为
(6)
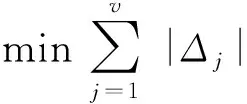
耦合度к的物理意义:①к反映了BKC内各回路变量之间的关联、依赖程度,且已证明:к值越大,机构运动学、动力学问题求解的复杂度越高。②机构的位置正解求解可转换为其各个BKC的位置求解。③对于к=0的BKC,其每个回路的运动量解析解都能独立求出;若к>0,意味着BKC的运动量需多个回路方程联立求解,可用к维搜索法或代数法求得其位置正解或动力学逆解。
(2)机构耦合度к计算
1.2.2节已计算出2个回路的独立位移方程数,分别为ξL1=5,ξL2=6,因此,它们的约束度Δ1、Δ2为
因此,该机构包含2个BKC,即第1个独立回路为BKC1,第2个独立回路为BKC2。由式(6)得,耦合度分别为:к1=0、к2=0;因此,它们运动学正解可分别直接求出解析式。
2 机构的位置分析
2.1 位置正解求解
2.1.1坐标系的建立与参数标注
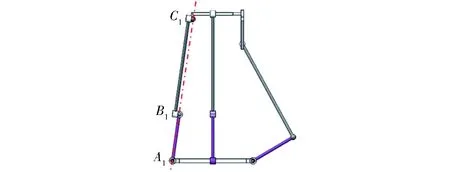
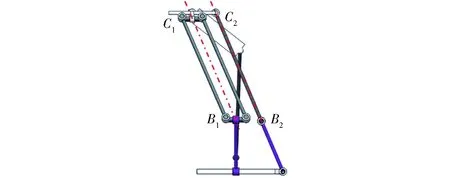
2T1R机构的运动学建模如图2所示,静坐标系oxyz建立在静平台0的几何中心,且x轴与A1A3连线重合,y轴与A1A3连线垂直,z轴由右手法则确定;动坐标系puvw的原点p位于直线C3D3中点,v、u轴分别重合、垂直于直线C3D3,w轴同样由右手法则确定。
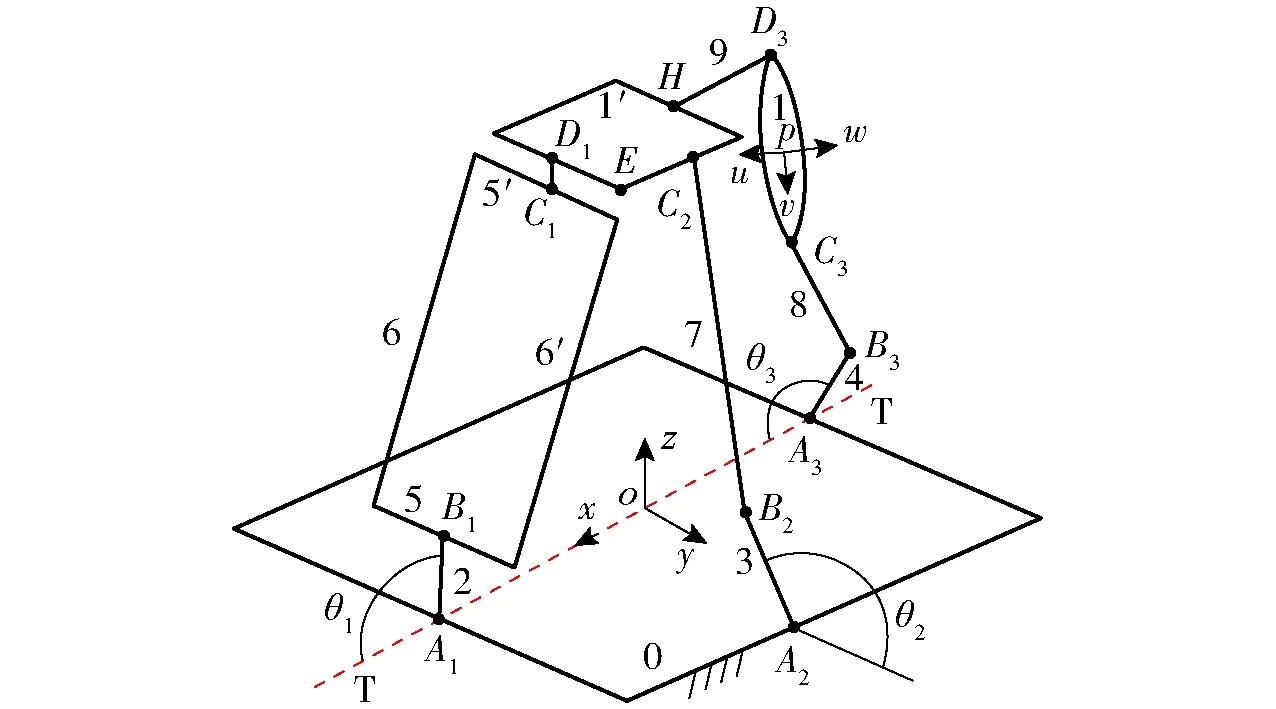
图2 (RPa‖3R)-R+RSS机构的运动学建模Fig.2 Kinematics model of mechanism(RPa‖3R)-R+RSS
该机构的结构参数为:静平台0上点A1、A2和A3到原点O的距离均为l,即OAi=l(i=1,2,3);C3D3=l8;杆2、3、4的长均为l1,即AiBi=l1(i=1,2,3);杆6的长为l2,即B1C1=l2;杆7、8的长分别为l3、l5,即B2C2=l3,B3C3=l5;其余参数分别为C1D1=l4;D1E=EC2=l6;HD3=l7。
设A1B1、A3B3与x轴正向的夹角为θ1、θ3;A2B2与y轴正向的夹角为θ2;求动平台1上p的坐标(x,y,z)及其姿态角θ。
2.1.2BKC1的位置分析
在静坐标系oxyz中,点Ai(i=1,2,3)、Bi(i=1,2)的坐标分别为A1=(l,0,0)、A2=(0,l,0)、A3=(-l,0,0);B1=(l+l1cosθ1,0,l1sinθ1)、B2=(0,l+l1cosθ2,l1sinθ2)。
由1.2.1节可知:机构运动过程中,子平台1′仅产生沿z、y轴的平移,即xC2=0;则C1、C2的坐标分别为C1=(l-l6,yC2-l6,zC2-l4)、C2=(0,yC2,zC2)。
于是,由杆长约束B1C1=l2,B2C2=l3,有位置约束方程
(7)
简化式(7)得
ayC2+bzC2=c
(8)
其中a=2(yB2-2l6)b=2(zB2-l4-xB1)
若a=0且b=0,则
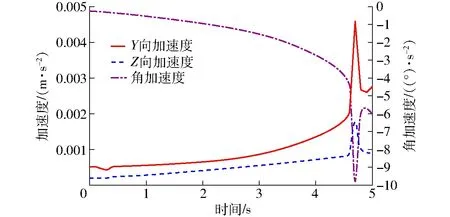
但因l2 (1)当a=0时 (9) (2)当a≠0时 (10) 其中d=a2+b2e=2(bc+zB2a2-abyB2) 2.1.3BKC2的位置求解 (11) 而C3点的坐标为 (12) 因此,由D3、C3点坐标,易求解p点的坐标(x,y,z)。 进一步,由杆长约束B3C3=l5,得位置方程 (13) 将式(13)整理化简得 a1sinθ+b1cosθ+c1=0 (14) 其中a1=2c2l8b1=2b2l8 b2=(yB3-y)2c2=(zB3-z)2 (15) 从而求得该机构动平台1的姿态角。 已知:动平台1上p的坐标(x,y,z)和姿态角θ,求输入角θ1、θ2、θ3。 C3、D3、H点的坐标分别为 而C1、C2点的坐标分别为 C1=(l6,yH,zH-l4)C2=(0,yH+l6,zH) 由杆6、7、8的3个杆长约束,可建立方程 (16) (17) (18) 由式(16)~(18)可得 (19) 其中z1=zC1z2=zC2z3=zC3 综上可知,当动平台p(x,y,z)已知时,输入角θ1、θ2、θ3各有两组解,即C1、C2、C3点的坐标各有两组解,故逆解数为8,因此,动平台有8种构型。 参考ABB机器人I4R的尺寸参数,输入杆和平行四边形的尺寸参数与之相同[28],即l1=350 mm、l2=750 mm;其他结构参数分别为l=300 mm、l3=l5=800 mm、l4=40 mm、l6=150 mm、l7=70 mm、l8=390 mm。 取3个输入角θ1、θ2、θ3分别为36.08°、66.74°、161.86°。由Matlab计算得该机构的位置正解,如表1所示。 表1 位置正解数值Tab.1 Numerical values of direct kinematics 对应1组解的机构三维构型如图3所示。 图3 对应1组解的机构构型Fig.3 Configuration of solution 1 取表1中的1组解的数据,代入逆解式(19),计算求得8组逆解数值,如表2所示。 由表2知,第1组逆解数值,与正解求解时3个设定的输入角一致,因此,正逆解公式推导正确。 表2位置逆解数值 Tab.2 Numerical values of inverse kinematic (°) 图5 机构工作空间各点的转角范围Fig.5 Range of rotational angle of any point in workspace 采用极坐标空间三位搜索法,基于机构的位置逆解,查找该机构工作空间内所有满足杆长约束、转角约束、干涉约束的点,即预先设定该机构工作空间的z向高度范围,通过改变搜索半径以及搜索角度,找到工作空间的边界。 设定搜索范围为:0≤z≤1 200 mm, -π≤θ≤π,0≤ρ≤300 mm;基于位置逆解式(19),由Matlab软件编程,得到机构可达工作空间如图4所示。 图4 机构的工作空间Fig.4 Workspace of PM 由图4可知: (1)机构的工作空间为平行于yoz面的一个“桥孔型”平面区域,且相对于x轴(T-T直线)具有良好的对称性,这与实际结构关于T-T对称一致。 (2)当z≤400 mm时,该机构的工作空间不连续,存在空洞。 (3)当410 mm≤z≤1 500 mm时,“桥孔型”平面型工作空间连续,为可达工作空间;在可达空间内会存在运动奇异现象,具体分析详见第4节。 机构的动平台转角分析是评估并联机构转动角度能够到达的范围。同样,基于机构的位置逆解方程,采用极限边界搜索法,可以求出机构动平台基点在工作空间内任意位置时的转角范围。 由1.2.1节机构的POC分析可知,动平台1的运动输出为oyz平面内的两维平移2T;当400 mm≤z≤1 200 mm时,由Matlab计算出基点在oyz平面上各点时,则转角θ的运动范围如图5所示。 由图5可知,机构工作空间内各点的转角θ的范围较大,由图5可看出: (1)动平台处于点A(0,900)、B(-600,700)时,其转角范围分别为[-180°,180°]、[-120°,90°]。 (2)A点分别处于红色、蓝色区域内,机构的转角能达到[-180°,180°],约占总区域面积的70%,表明机构的动平台1具有较大的转动能力。 JpV=Jqω (20) 其中 u11=2(zC1-zB1)l1cosθ1+2(xC1-xB1)l1sinθ1 依据Jp、Jq矩阵是否奇异,将机构的奇异位形分为如下3类:①当det(Jq)=0时,机构发生输入奇异。②当det(Jp)=0时,机构发生输出奇异。③当det(Jq)=det(Jp)=0时,机构发生综合奇异。 4.2.1输入奇异 机构发生输入奇异,意味着每条支链靠近驱动杆的两根杆处于折叠在一起或完全展开状态。这时,动平台的自由度数减少。此时,det(Jq)=0,该行列式方程解的集合K为 K={K1∪K2∪K3} (21) 且3种情况分别为:①K1={(xC1-xB1)sinθ1+(zB1-zC1)cosθ1=0},即A1、B1、C1三点在oxz平面上的投影共线。②K2={(yC2-yB2)sinθ2+(zB2-zC2)·cosθ2=0},即A2、B2、C2三点共线。③K3={(zB3-zC3)cosθ3+(xC3-xB3)sinθ3=0},即A3、B3、C3三点在oxz平面上的投影共线。 满足K1的三维构型如图6所示。 图6 输入奇异位形Fig.6 Structure of input singularity 4.2.2输出奇异 机构发生输出奇异,意味着每条支链靠近动平台的杆处于折叠在一起或完全展开的状态,此时的动平台自由度数增多,即使锁住输入,动平台也可能存在自由度输出。设 (wi1,wi2,wi3)=ei(i=1,2,3) (22) (wk1,wk2,wk3,wk4)=Ek(k=1,2,3) (23) 若det(Jp)=0,则向量e1、e2、e3有如下2种情况: (1)存在2个向量线性相关 ①若e1=ke2,取w12=kw22,则 kw23=kl8(yC2-yB2)sinθ≡w13 即E1≡kE2,其三维构型为向量lB1C1、lB2C2在oyz平面上的投影相互平行,如图7所示。 图7 输出奇异位形(例1)Fig.7 Structure of output singularity (example 1) ②若e2=ke3,取w21=kw31,则 kw33=k[2l8(xB3-xC3)cosθ-l8yC3sinθ] 图8 输出奇异位形(例2)Fig.8 Structure of output singularity (example 2) 同理可得:e1=ke3,E1≡kE3。 (2)存在3个向量线性相关 若e1=k1e2+k2e3(k1k2≠0),即 w1i=k1w2i+k2w3i(i=1,2,3) 同理,可得:任意3个向量(k1k2≠0)均线性无关则第2种情况都不成立。 4.2.3综合奇异 此时,det(Jq)=det(Jp)=0,即输入奇异和输出奇异同时发生。在此位形下,动平台将失去原有的运动特性。因此,取满足输入奇异中的K1、K2、K3的条件,代入输出奇异分析中,此时,输出奇异不成立,故该机构不存在综合奇异。 当机构非奇异时,Jp可逆,可得 (24) 式(24)即为动平台原点的输出速度。 进一步,对式(24)求导得到 (25) 当机构不存在奇异性时,Jp可逆,则 (26) 式(26)即为动平台原点的加速度公式。 表3 动平台的速度分析Tab.3 Velocity of moving platform 表4 动平台的加速度分析Tab.4 Acceleration of moving platform 将该并联机构的三维模型,通过Solidworks导入到ADAMS软件中进行仿真,得到动平台的速度与加速度曲线分别如图9、10所示。 图9 动平台的速度曲线Fig.9 Curves of velocity of moving platform 图10 动平台的加速度曲线Fig.10 Curves of acceleration of moving platform 由表4及图10可知: (1)由Matlab计算得到加速度(表4,t=2 s时,ay=0.642 mm/s2,az=0.455 mm/s2,aw=-0.982(°)/s2与运用ADAMS仿真得到的加速度(图10,t=2 s时ay=0.64 mm/s2,az=0.45 mm/s2,aw=-0.98(°)/s2)完全一致,从而验证了推导的速度与加速度公式的正确性。 (2)机构动平台的速度、加速度曲线,变化较平 稳、连续,表明机构的动力学性能较好。 (1)提出了一种空间2T1R无寄生运动的非全对称并联机构(RPa‖3R)-R+RSS;该机构耦合度为零且具有部分运动解耦性;给出了该机构位置正、反解的解析式。 (2)当410 mm≤z≤1 500 mm时,平行于yoz面的“桥孔型”平面型工作空间连续,为有效作业区域,且具有较好的对称性。 (3)机构平台转动能力分析表明:动平台转角θ的范围较大,能达到[-180°,180°]的区域约占总区域70%,动平台具有较大的转动能力。 (4)机构速度与加速度仿真曲线表明,机构动平台加速度变化较平稳,具有较好的动力学性能。 1 黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1996. 2 HUANG Z,FANG Y F. Kinematics characteristics analysis of 3-DOF parallel actuated pyramid mechanisms[J]. Mechanism and Machine Theory,1996,31(8):1009-1018. 3 GROGORIOR D.Kinematics of a new spherical manipulator with three equal legs: the 3-URC wrist[J]. Journal of Robotic Systems,2001,18(5):213-219. 4 于海波,赵铁石,李仕华.空间3-SPS/S对顶双锥机构的运动学分析[J].机械设计,2007,24(2):11-14. YU Haibo,ZHAO Tieshi,LI Shihua. The kinematic analysis of top double cone mechanism of spatial 3-SPS/S[J]. Journal of Mechanism Design,2007,24(2):11-14.(in Chinese) 5 LI Q,HERVE J M. 1T2R parallel mechanisms without parasitic motion[J]. Robotics,IEEE Transactions on,2010,26(3):401-410. 6 NEUMANN K E. Robot:US,4732525[P]. 1988-03-22. 7 OLAZAGOITIA J L,WYATT S. New PKM Tricept T9000 and its application to flexible manufacturing at aerospace industry[C]. SAE Paper 07ATC(-94),2007. 8 NEUMANN K E. Parallel-kinematical machine:WO/2006/054935[P]. 2006-02-26. 9 ZOPPI M,ZLATANOV D,MOLFINO R. Kinematics analysis of the Exechon tripod[C]∥Proceedings of the ASME 2010 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE,Quebec,Canada 2010:1-8. 10 HUANG T,LI M,ZHAO X M,et al. Conceptual design and dimensional synthesis for a 3-DOF module of the TriVariant—a novel 5-DOF reconfigurable hybrid robot[J]. IEEE Transaction on Robotics,2005,21(3):449-456. 11 王飞博,吴伟峰,陈祥,等. 基于运动/力传递特性的1T2R并联机构构型优选[J]. 机械工程学报,2014,50(23):20-28. WANG Feibo,WU Weifeng,CHEN Xiang,et al. Optimal type selection of 1T2R parallel mechanisms based on motion/force transmissibility[J]. Journal of Mechanical Engineering,2014,50(23):20-28.(in Chinese) 12 汪满新,黄田. 1T2R 3自由度并联机构拓扑结构综合[J]. 机械工程学报,2015,51(17):1-7. WANG Manxin,HUANG Tian. Type synthesis of 1T2R 3-DOF parallel mechanism[J]. Journal of Mechanical Engineering,2015,51(17):1-7.(in Chinese) 13 HUNT K. Structural kinematics of in-parallel-actuated robot-arms[J]. Journal of Mechanical Design,1983,105(4):705-712. 14 JOSHI S A,TSAI L W. Jacobian analysis of limited-DOF parallel manipulators[J]. Journal of Mechanical Design,2002,124(2):254-258. 15 KONG X W, GOSSELIN C M. Type synthesis of 3-DOF PPR- equivalent parallel manipulators based on screw theory and the concept of virtual chain[J]. ASME Journal of Mechanical Design,2005,127: 1113-1121. 16 杨宁,马履中,艾永强,等.两平移一转动并联机构型综合研究[J].机械设计与研究,2005,21(5): 29-32. YANG Ning,MA Lüzhong,AI Yongqiang,et al. Study on structure synthesis of two translations and one ratation parallel mechanism[J]. Machine Design and Research,2005,21(5): 29-32.(in Chinese) 17 REFAAT S,HERVE J M,NAHAVANDI S.A symmetrical three-DOFs rotational-translational parallel-kinematics mechanisms based on lie group theory[J]. European Journal of Mechanics A/Solids,2006,25:550-558. 18 张彦斌,吴鑫,刘宏昭,等.无奇异完全各向同性2T1R型并联机构的结构综合[J].中国机械工程,2008,19(3): 277-281. ZHANG Yanbin,WU Xin,LIU Hongzhao,et al. Structural synthesis of singularity-free fully-isotropic parallel mechanisms with 2T1R-type[J]. China Mechanical Engineering,2008,19(3): 277-281.(in Chinese) 19 杨廷力.机器人机构拓扑结构学[M].北京:机械工业出版社,2004. 20 杨廷力,刘安心,罗玉峰,等. 机器人机构拓扑结构设计[M]. 北京:科学出版社,2012. 21 YANG Tingli,LIU Anxin,SHEN Huiping,et al. Topology design of robot mechanisms[M]. Springer,2018. 22 SHEN Huiping,ZHU Xiaorong, ZHANG Dan,et al. The design methodology for less input-more output parallel mechanisms[J]. Mechanism and Machine Theory,2016,104(10):43-58. 23 沈惠平,邓嘉鸣,孟庆梅,等. 少输入-多输出并联机构的设计方法及其应用[J]. 机械工程学报,2018,54(1):223-232. SHEN Huiping,DENG Jiaming,MENG Qingmei,et al. Design methods and applications for the fewer input-more output parallel mechanisms[J]. Journal of Mechanical Engineering,2018,54(1):223-232.(in Chinese) 24 邓嘉鸣,沈惠平,李菊,等.三维并联振动筛设计与实验[J/OL]. 农业机械学报,2013,44(11):342-346. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20131157&flag=1. DOI:10.6041/j.issn.1000-1298.2013.11.057. DENG Jiaming,SHEN Huiping,LI Ju,et al. Design and experiment research for three-dimensional parallel kinematics vibration sieve[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(11):342-346.(in Chinese) 25 李菊,曾氢菲,邓嘉鸣,等.多维并联振动筛筛分过程解析与筛面运动形式优选[J/OL].农业机械学报,2016,47(11):399-407. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161154&flag=1. DOI:10.6041/j.issn.1000-1298.2016.11.054. LI Ju,ZENG Qingfei,DENG Jiaming,et al. Screening process analysis for multidimensional parallel vibrating screen and optimization of screen surface movement[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(11):399-407. (in Chinese) 26 沈惠平,杨梁杰,邓嘉鸣.用于肩关节康复训练的单输入三转动输出并联机构及其运动学设计[J]. 中国机械工程,2015,26(22):2983-2988. SHEN Huiping,YANG Liangjie,DENG Jiaming. A one-input three-rotation output parallel mechanism used for shoulder rehabilitation and its kinematics design [J]. China Mechanical Engineering,2015,26(22):2983-2988.(in Chinese) 27 邓嘉鸣,戴丽芳,沈惠平,等.并联式脚底按摩机构的设计及其研制[J]. 机械设计,2016,33(2):78-82. DENG Jiaming,DAI Lifang,SHEN Huiping,et al. A novel parallel foot massage mechanism and its kinematics design[J].Journal of Machine Design,2016,33(2):78-82.(in Chinese) 28 刘平松,郭钢,朱海宁. 4R并联机器人工作空间分析[J]. 机械制造与自动化,2012,41(4):156-157. LIU Pingsong,GUO Gang,ZHU Haining.Workspace analysis of the I4R parallel robot[J]. Machine Building & Automation,2012,41(4): 156-157.(in Chinese)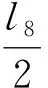
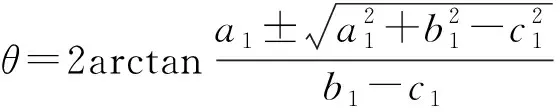
2.2 位置逆解求解
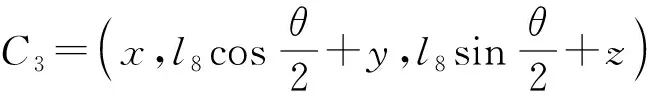
2.3 正逆解验算

3 机构的工作空间和转动能力分析
3.1 工作空间分析


3.2 转动能力分析
4 机构的奇异性分析
4.1 机构奇异性原理
u22=2(zB2-zC2)l1cosθ2+2(yC2-yB2)l1sinθ2
u33=2(zB3-zC)l1cosθ3+2(xC3-xB3)l1sinθ3
v11=2yC1v21=2(yC2-yB2)v31=2yC3
v12=2(zC1-zB1)v22=2(zC2-zB2)
v32=2(zC3-zB3)
v13=l8yC1sinθv23=l8(yC2-yB2)sinθ
v33=2l8(xB3-xC3)cosθ-l8yC3sinθ4.2 奇异位形分析
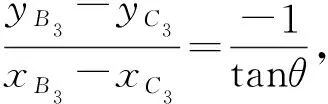
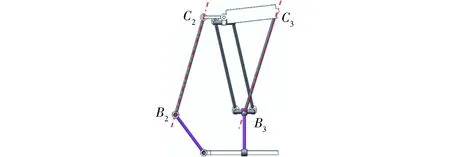
k1w23+k2w33=k1l8(yC2-yB2)sinθ+
k2[2l8(xB3-xC3)cosθ-l8yC3sinθ]≠w135 机构速度和加速度分析
5.1 速度公式推导
5.2 加速度公式推导
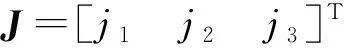
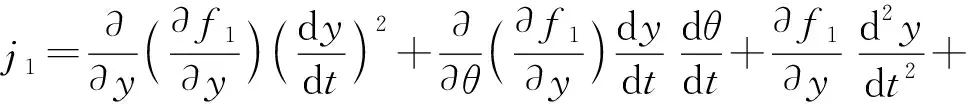
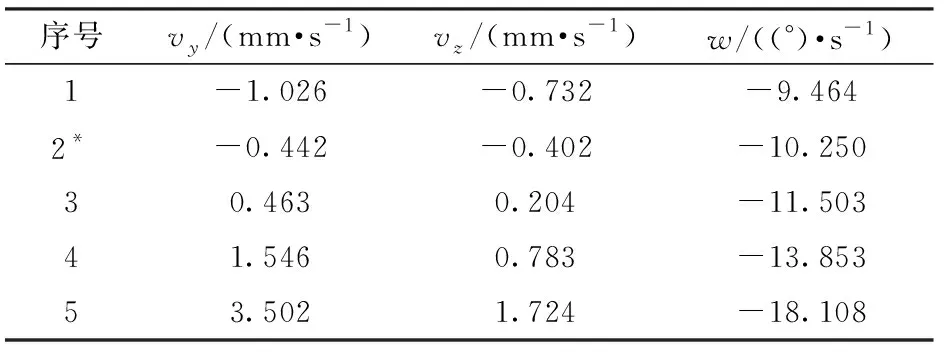
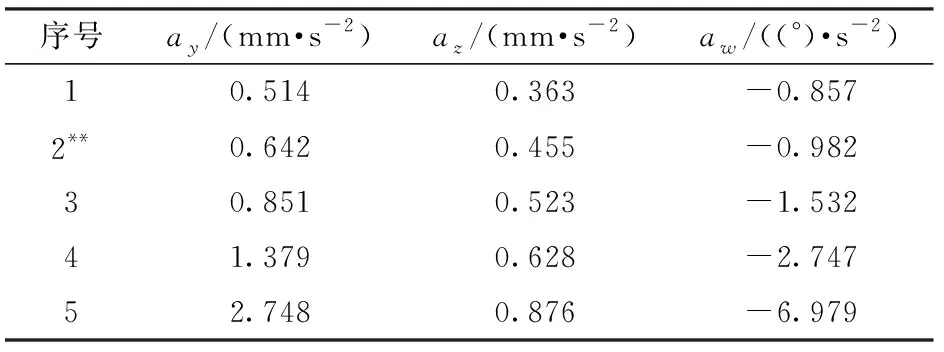
5.3 速度和加速度算例验证

6 结论

