基于轨迹跟踪的农用履带机器人自适应滑模控制
许正荣, 王文周, 辜丽川, 乔 焰, 褚刚秀, 焦 俊
(安徽农业大学信息与计算机学院,安徽 合肥 230036)
由于农用履带机器人(Agricultural tracked robot, ATR)具有体积小、活动范围大等优点,已经在农田环境监测、农产品采摘等领域获得高度重视。对ATR进行稳定、精确的控制是ATR的关键技术之一[1-2]。但是ATR运动方程的非线性、耦合性、系统参数的时变性,以及农田地形复杂性、环境多变性都给ATR的控制增加了难度,常规的线性控制法难以满足农业实际应用需求和高精度的控制性能要求。一般的控制方法中,反馈线性化方法在系统存在不确定性,受到干扰时其鲁棒性没有保障[3];Backstepping法需要系统的模型满足状态线性化;神经网络控制法控制算法复杂[4];PID控制法对于非线性和结构不确定系统的控制效果较差[5];焦俊等[6]针对移动机器人动力学的高度非线性和运动环境的不确定性,提出基于模糊逻辑的移动机器人路径跟踪控制方法,该方法对于差动转向移动机器人的运动控制具有普适性,但其对较大曲率的轨迹跟踪效果表现欠佳。
滑模变结构控制不依赖被控对象精确的数学模型,具有对参数和环境变化不敏感和工程实现简单的特性,然而,“抖振”问题是滑模控制本身固有的缺陷,它会使机器人的执行机构在频繁切换中出现故障,降低系统稳定性。对此,有研究者试图通过在切换函数中增加积分项来解决这一问题,虽然积分项在一定程度上降低了“抖振”,但是随着积分项的引入,又会导致在初始误差较大的情况下,出现积分饱和现象,使系统出现大幅度超调,甚至不稳定[7-10],阻碍了滑模控制的应用。
为了解决该问题,本研究从控制策略角度出发,构建变倾斜参数的自适应积分滑模切换函数,基于该函数提出由等效控制和切换控制组成的自适应滑模跟踪控制,将机器人的速度和位姿误差反馈至变结构控制中,然后根据运动学关系,分解驱动轮的期望速度,同时从理论上分析证明该控制方法的可达性和稳定性,从仿真和试验上验证该控制方法的有效性。
1 轨迹跟踪的位姿误差模型
ATR的几何结构俯视图以及坐标系定义的简化图如图1所示, 其中XOY、xboayb分别为惯性坐标系和跟踪坐标系,ATR状态由质心Oa在XOY坐标系中的位置及航向θ来表示,其中(x,y)为机器人质心在XOY坐标系中的坐标,θ为ATR运动方向和X轴的夹角,ν和ω分别表示ATR的线速度和角速度[11-12],p为机器人的几何中心,d为质心p与几何中心Oa之间的距离,驱动轮半径为r,两轮间轴向距离为2A。根据图1得到履带机器人运动学模型为式(1),ATR的实际位姿为p=(X,Y,θ),期望位姿为pr=(Xr,Yr,θr)T,ATR的位姿误差如图2所示。
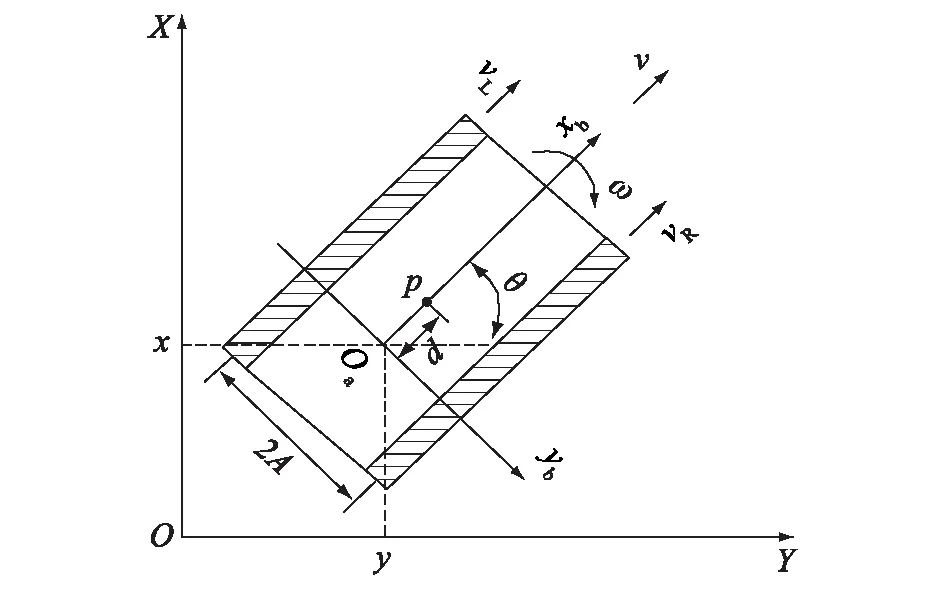
图1 机器人模型Fig.1 Sketch of agricultural tracked robot(ATR) model

图2 位姿误差示意图Fig.2 Sketch map of position and orientation error
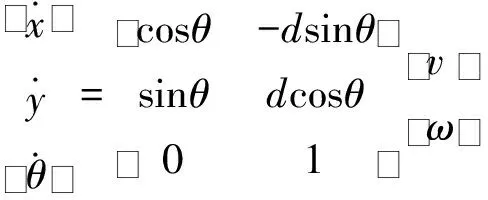
(1)
轨迹跟踪误差为式(2):
(2)
式中,xe和ye分别为xb轴和yb轴向误差,θe为航向角误差,将式(2)微分,结合式(1)得到如式(3)的位姿误差微分方程。
(3)
2 自适应滑模轨迹跟踪控制设计
为了实现ATR的自适应滑模轨迹跟踪控制(Adaptive sliding mode trajectory tracking control, ASMTTC),在分析了位姿误差模型和滑模“抖振”对系统稳定性影响的基础上,构建基于变sigmoid的积分切换函数的ASMTTC,将位姿误差和可调参数反馈至ASMTTC中,ASMTTC再输出左右驱动轮角速度,使得ATR的位姿满足式(4),ASMTTC控制系统结构如图3所示。
(4)
式中p是机器人位姿,pr是期望位姿。
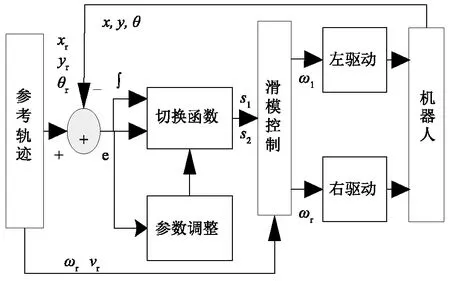
图3 自适应滑模控制结构图Fig.3 Structure diagram of adaptive sliding mode trajectory tracking control (ASMTTC)
2.1 切换函数的设计
针对位姿误差微分方程式(3)的特点,设计基于变倾斜参数的Sigmoid滑模切换函数式(5)。由于使用了具有饱和特性的非线性函数,这样在出现较大位姿误差时,就抑制了积分项的作用,避免出现较大的超调;在误差较小时具有一定的放大作用,在不引起“抖振”的情况下使控制精度得到提高[13-14]。
(5)
式中kk1、kk2均为正常数,α1、α2为倾斜参数,其自适应调节公式为式(6)。
(6)
式中c1、c2、c3、c4均为正常数,从式(6)可知,α1、α2随着位姿误差的减小而增大。
2.2 滑模控制律设计
对式(5)求导可得式(7)。
(7)
将式(3)代入式(7),得式(8)。
(8)
令式(8)等于0,得到等效控制式(9)。
(9)
式中Ueq是等效控制。令切换控制为:
(10)
式中β1、β2为切换增益,均大于0;sat( )为饱和函数;△1、△2为边界层厚度。若边界层厚度值较大,抗“抖振”能力较强,会降低控制精度;若厚度值较小,能够提高控制精度,但易引起“抖振”。
综合式(9)和式(10),得到总的滑模控制律U=Ueq+Usw。
(11)
2.3 稳定性分析
从边界层的可达性和边界层内系统平衡点的稳定性方面分析证明,ASMTTC可以控制机器人跟踪轨迹收敛于平衡点[15-18],即跟踪位姿误差趋于0。
定理1:考虑系统式(3),按式(5)构造切换函数,若采用式(11)所示的滑模控制律,则式(3)所描述的系统将在有限时间内到达滑模边界。
证明:以s1为切换函数为证明实例,当系统到达边界层时,存在式(12)
(12)
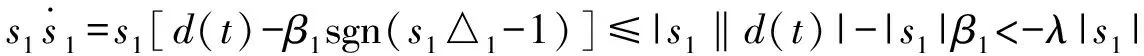
(13)
(1)当s1>0时,当系统到达滑模边界层时,t=t0,s1(t0)=△1。由式(13),可得式(14),
(14)
(2)当s1<0时,若系统到达滑模边界层,s1(t0)=-△1,由式(13),可得式(15)。
(15)
(3)当s1=0时,t=t0=0,系统到达滑模边界层内。
因为△1,λ是有界常实数,所以从上述3种情况可知,在切换函数初值s1(0)有界的条件下,可以在有限时间内到达滑模边界层,到达时间t0<[s1(0)-△1]λ-1。

证明:以切换函数s1为证明实例,当系统到达滑模边界层后,存在
(16)
记ρ为拉普拉斯变换算子,对式(16)进行拉普拉斯变换,s1,d(t)拉普拉斯变换后分别为s1(ρ),d(ρ),得到

(17)
结合拉普拉斯变换终值定理,可得
(18)
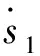
(19)
运用Lyapunov函数
(20)
显然,V>0,并且满足|xe|→时,|V|→,是径向无界,存在
(21)
当t→时,依据式(19)可得
因此,存在
(22)
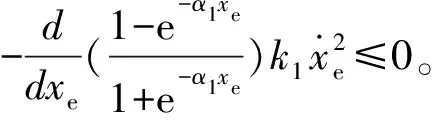
2.4 驱动控制
根据式(11),当运动学模型输入一个速度[vdωd]T时,相应的左、右驱动轮输出的角速度为ωld、ωrd:
ωld=(vd(t)-ωdA)r-1
(24)
ωrd=(vd(t)+ωdA)r-1
(25)
3 仿真及结果分析
为了检验所设计控制算法的有效性,运用MATLAB搭建仿真模型,对ATR控制系统进行仿真分析,机器人长度L=0.55 m,宽度W=0.4 m,驱动轮半径r=0.1 m,两驱动轮轴间距2A=0.36 m。控制器参数:kk1=kk2=2,c1=c3=2,c3=c4=4,kωl=kωr=1 000,仿真采样时间为50 ms。
3.1 基于ASMTTC与SMC的阶跃信号响应特性分析
分别采用ASMTTC和指数趋近律的滑模控制(Sliding mode control,SMC)对初始值为0、最大值为20 rad/s的阶跃信号进行仿真控制研究。由于左、右驱动轮的仿真条件、参数和模型一样,因此本仿真只列出左驱动轮的阶跃响应特性曲线。由图4可知,在ASMTTC调节下,驱动轮角速度从0开始,响应曲线平滑,系统在0.375 s达到稳定状态,输出角速度的终止值为20 rad/s,角速度跟踪误差从-20 rad/s收敛趋近于0。这是由于ASMTTC中滑模切换函数中采用了变倾斜参数的积分项,在系统出现较大误差情况时,能够限制积分项作用,使系统不出现过大的超调;在误差较小时有放大作用,在不引起抖振的情况下改善控制精度。而在SMC控制时,系统需要0.75 s才能达到稳定状态,且有抖振现象。
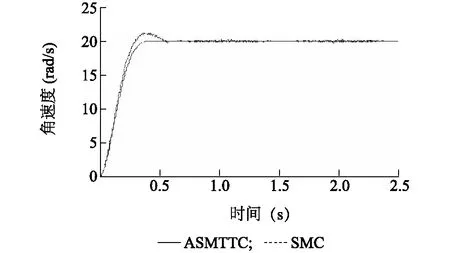
图4 ASMTTC和SMC的阶跃响应曲线Fig.4 Step response curves of ASMTTC and SMC
3.2 基于ASMTTC折线轨迹的跟踪控制
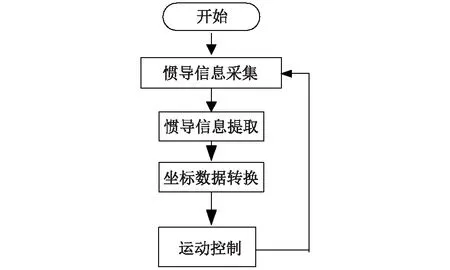
以折线为参考轨迹,其初始位姿为[0,0,pi/4]T,ATR初始位姿为[-2,-2,pi/4]T,ATR速度为2 m/s,仿真时间0 选取半径为10 m的圆形轨迹:x=10 cosθ、y=10 sinθ为参考路径,轨迹初始位姿为[10,0,pi/2]T,ATR的初始位姿为[7,0,pi/2]T,左右驱动轮角速度都从0开始,分别达到10 rad/s、30 rad/s后,ATR以2 m/s速度逆时针方向运行,仿真时间0 图5 折线轨迹跟踪结果(a)及误差曲线(b)Fig.5 Tracking result (a)and error curve (b)of fold line trajectory 图6 圆轨迹跟踪结果(a)及误差曲线(b)Fig.6 Tracking result (a)and error curve (b)of circular trajectory 为了验证ASMTTC的正确性和有效性,构建基于S3C2440的控制系统,以自主研发的ATR为控制对象,进行野外控制试验。 控制器系统主要完成对惯导信息采集和履带机器人的控制。根据控制策略与控制算法构建由硬件和软件两部分组成的控制系统。硬件部分包括S3C2440微处理器、存储模块、惯导系统、传感器模块、电机驱动单元、数据通信模块和电源等,其中微控制器模块负责整个数据的处理和运算,存储模块负责信息存储,电机驱动单元驱动机器人运行,传感器模块负责采集现场信息,电源模块为电路提供工作电压,数据通信模块负责与远端服务器进行信息通信。控制器结构见图7,实物见图8。 图7 控制器硬件结构Fig.7 The hardware structure of controller 图8 控制器硬件实物图Fig.8 The hardware object of controller 控制软件运行在Linux操作系统环境下,主要由驱动和应用层程序组成。驱动程序与底层硬件紧密相连。应用层程序是根据编程接口(API)函数,针对控制需求而编写的应用程序。控制软件架构和软件流程分别如图9和图10所示。 图9 控制软件架构Fig.9 Structure diagram of control software 图10 控制软件流程图Fig.10 Flowchart of control software 在采集惯导数据之前,微处理器先初始化惯导的数据格式和更新率。惯导经过内部差分解算处理后,输出格式和含义如表1所示的ASCII码数据,数据间以逗号隔开,从串口传给微处理器。微处理器对接收的惯导数据进行坐标转换,存储位姿信息,计算控制量。程序流程见图11。 表1 SPAN-CPT的数据格式(标准国际单位) 图11 惯导数据采集与处理流程Fig.11 Data collection and processing of the inertial navigation system 为了计算ATR位姿误差,需要实现大地坐标与笛卡尔坐标的转换,转换程序如下: void GdToCt (PCRDCARTESIANdkp, PCRDGEODETICddp,doublecbz, doublebl) // dkp:笛卡尔坐标指针;ddp:大地坐标指针;cbz:参考椭球的长半轴;bl:参考椭球的扁率。 天津滨海新区是国家发展战略的重要一极,是中国的,更是世界的。一个面向世界的国际化城市不能没有自己的城市品牌,特别是在西方发达城市普遍重视建设自己的城市品牌的形式下,天津滨海新区城市品牌的建设显得尤为重要,也尤为迫切。 { doublef; //偏心率平方 doubler; //卯酉圈半径 f=2*bl-bl*bl; r=cbz/sqrt(1-f*sin(ddp→latitude)*sin(ddp→latitude)); dkp→x=(r+ddp→height)*cos(ddp→latitude)*cos(ddp→longitude); dkp→y=(r+ddp→height)*cos(ddp→latitude)*sin(ddp→longitude); dkp→z=(r*(1-f)+ddp→height)*sin(ddp→latitude); } static unsigned int fuzh( unsigned int *mmap_addr , unsigned int zh ,unsigned int clsf ,unsigned char m) // mmap_addr:映射寄存器的地址;zh:要设置的值;clsf:清除标志;m:清除的位置 { unsigned int tmp1; //暂存寄存器值 unsigned int tmp2; tmp2 = ioread32( mmap_addr );//读取寄存器的值 tmp1 = tmp2; tmp2 = tmp2 & (~(clsf << m)); //清除tmp2对应位 tmp2 = tmp2 | zh << m;// 设置tmp2对应位 iowrite32( tmp2 , mmap_addr );//将tmp2值写入mmap_addr寄存器 return tmp1 } ; //返回原来寄存器的值 野外控制试验在长有杂草的沙壤土农田中进行(图12)。以ATR上安装的惯导SPAN-CPT作为状态信息获取设备,状态信息更新率是10 Hz,速度精度是0.01 m/s,角度精度是0.02 rad,位置测量精度是0.01 m。 图12 试验中履带机器人Fig.12 ATR used in actual experiment ATR参考路径为 (26) ATR长度L=0.55 m,宽度W=0.4 m,驱动轮半径r=0.1 m,两驱动轮轴间距2A=0.36 m,ATR运行速度为2 m/s,履带机器人的初始位姿为 [x(0)y(0)θ(0)]T=[0 20 π/12]T 期望位姿为 [x(0)y(0)θ(0)]T=[10 40 π/4]T 初始位姿误差为 [xe(0)ye(0)θe(0)]T=[10 20 π/6]T ASMTTC对ATR控制后的轨迹结果显示,除初始位置和参考轨迹曲率变化较大的区域外,其他区域的跟踪轨迹较为平滑(图13)。从ASMTTC控制下产生的误差曲线图中可以发现,在ATR运动的初始阶段,由于ATR初始位姿与初始命令位姿不一致,使得初始位姿误差较大,在39~50 s和79~90 s期间,由于路径曲率变化较大,机械转向幅度较大,ATR受到的侧滑和离心力影响也较为严重,引起较大的位姿误差,所产生的xe、ye、θe误差范围分别为-0.03~0.04 m、-0.08~0.06 m、-0.03~0.05 rad。ATR运行在曲率变化较小的区域时,跟踪轨迹十分平滑,实际运行轨迹与参考轨迹之间的误差较小,趋近于0。 a:轨迹跟踪曲线;b:轨迹跟踪误差曲线。图13 ATR曲线轨迹跟踪结果Fig.13 Tracking result of curve trajectory for ATR 在相同试验条件、不同运行速度下,ATR对同一轨迹跟踪时产生的误差见表2。由表2可知,当ATR分别以1 m/s、3 m/s和4 m/s速度运行时,xb轴向的最小距离误差是-0.04 m,最大距离误差是0.04 m;yb轴向的最小距离误差是-0.09 m, 最大距离误差是0.07 m;航向角θe最小误差是-0.03 rad,最大误差是0.05 rad。可见,当以曲线和直线组合的路径为参考轨迹时,运用ASMTTC控制ATR,具有较好的稳定性和控制精度。 由于试验设备条件限制,目前ATR试验速度都比较低,高速和恶劣环境下的ASMTTC性能试验将是下一阶段的主要研究工作。 表2 低速条件下的轨迹跟踪位姿误差 针对ATR的轨迹跟踪问题,在运动学模型的基础上,构建了变倾斜参数的自适应积分滑模切换函数,基于这个函数提出了由等效控制和切换控制组成的自适应滑模跟踪控制。在出现较大位姿误差的情况下,切换函数能够限制积分项作用,使系统不出现过大的超调;在误差较小的情况下,有一定的放大作用,提高控制精度。在不引起抖振的条件下,消除静态误差,使控制精度得到提高。在1~4 m/s速度条件下,位姿参数误差范围分别为:-0.04≤xe≤0.04 m、-0.09≤ye≤0.07 m、-0.03≤θe≤0.05 rad。本研究结果表明ASMTTC能够满足ATR田间作业的实际需求。 参考文献: [1] 焦 俊,陈无畏,王继先,等. 基于GA和LS-SVM的AGV变结构控制[J].系统仿真学报,2008,20(14):3777-3781. [2] TEMEL T, ASHRAFIUON H. Sliding mode speed controller for tracking of under actuated surface vessels with extended kalman filter[J]. Electronics Letters, 2015, 51(6): 467-269. [3] BLAZIC S. A noval trajectory tracking control law for wheeled mobile robots[J]. Robotics and Autonomous Systems, 2011, 59(11): 1001-1007. [4] 焦 俊,江朝晖,金瑞春,等.农用机器人转向系统自适应内模控制[J].农业机械学报,2011,42(10):186-191,234. [5] ASIF M, KHAN M J, CAI N. Adaptive sliding mode dynamic controller with integrator in the loop for nonholonomic wheeled mobile robot trajectory tracking[J]. International Journal of Control, 2014, 87(5): 964-975. [6] 焦 俊,孔 文,王 强,等. 基于输入模糊化的农用履带机器人自适应滑模控制[J]. 农业机械学报,2015,46(6):14-19,13. [7] 熊中刚,叶振环,贺 娟,等. 基于免疫模糊 PID 的小型农业机械路径智能跟踪控制[J]. 机器人,2015,37(2):212-223. [8] 郑泽伟,霍 伟,诸 兵. 非完整移动机器人全局路径跟踪控制[J]. 控制理论与应用,2012,29(6):741-746. [9] CHEN C Y, LI T H S, YEH Y C, et al. Design and implementation of an adaptive sliding-mode dynamic controller for wheeled mobile robots[J]. Mechatronics, 2009, 19(2): 156-166. [10] 白晓平,胡静涛,高 雷,等. 农机导航自校正模型控制方法研究[J]. 农业机械学报,2015,46(2):1-7. [11] GHASEMI M, NERSESOV S G, CLAYTON G. Sliding mode coordination control for multiagent systems with under actuated agent dynamics[J]. International Jouranl of Control, 2014, 97(12): 2615-2633. [12] 焦 俊,汪宏喜,陈祎琼,等. 基于UKF的农用履带机器人滑动参数的估计[J]. 农业机械学报,2014,45(4):55-60. [13] CHEN X Q, LI J T. Sliding mode control for uncertain unified chaotic systems with nonlinear inputs[J]. Journal of Control Engineering, 2017, 24(1): 239-242. [14] WANG Z Y, LI Y D, ZHU L. Dual adaptive neural sliding mode control of non-holonomic mobile robot[J]. Journal of Mechanical Engineerin, 2010, 46(23): 16-22. [15] ZUO Z Y. Non-singular fixed-time terminal sliding model control of nonlinear systems[J]. Control Theory and Applications, 2015, 9(4): 545-552. [16] XU S D, CHEN C C, WU Z L. Study of nonsingular fast terminal sliding mode fault tolerant control[J]. IEEE Trans on Industrial Electronics, 2015, 62(6): 3906-3913. [17] MOSTASHFI A, FAKHARI A, MOHAMMAD A B. A novel design of inspection robot for high-voltage power lines[J].Industrial Robot An International Journal,2014,41(2):166-175. [18] 高为炳. 变结构控制的理论及设计方法[M]. 北京:科学出版社,1996:34-36.3.3 基于ASMTTC圆轨迹的跟踪控制


4 验证与分析
4.1 控制系统


4.2 控制软件


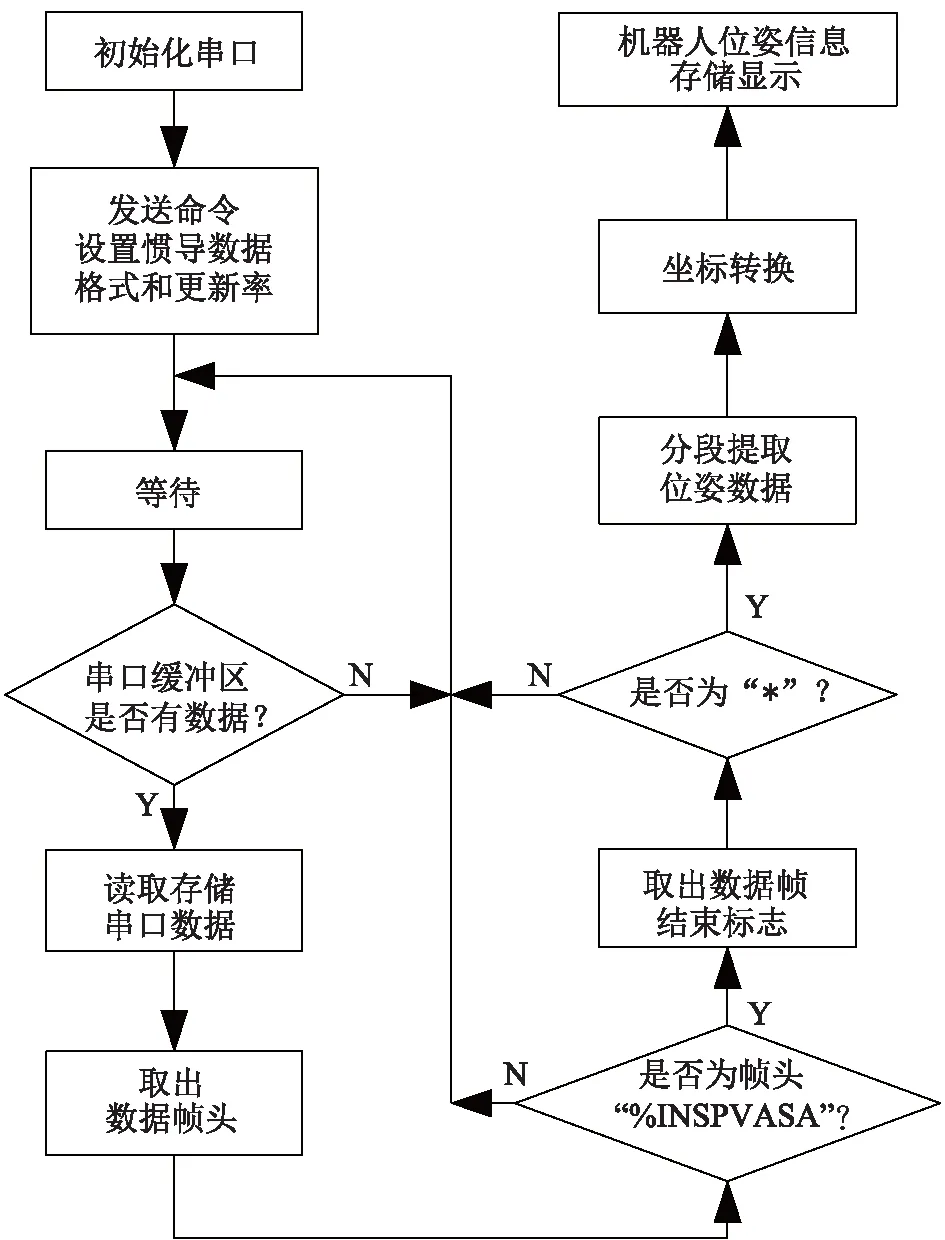

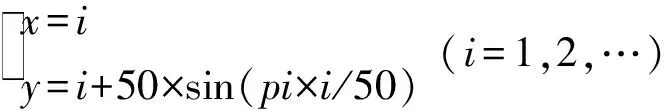
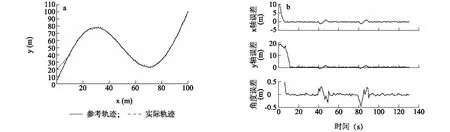

5 结 论

