噪声条件下对稀疏表示分类器的优化

陈浩

（上海海事大学信息工程学院，上海 201306）

0 引言

信号的稀疏表示在最近几年引起了广泛的兴趣，并在许多应用中显示出强大的特性，特别是在压缩和去燥方面。通过观察可以发现，大多数的自然信号可以适当的稀疏表示。稀疏信号表示的应用可以在诸如图像去噪[1]、恢复[2]、视觉跟踪[3]，检测[4]和分类[5]。Wright等人[6]通过研究提出了一种基于稀疏表示的分类方法（Sparse Representation Classification）。其基本思想是将测试样本的稀疏表示作为所有训练样本（超完备字典）的（稀疏）线性组合学习，其中产生最低重构误差的类的特定字典决定了测试样本的类标签。SRC也积极应用于各种分类问题，包括车辆分类、多模态生物特征、数字识别、语音识别、高光谱图像分类。

稀疏表示最稀疏的解决方案可以通过利用L0范数最小化来解决，已经证明L0范数最小化问题是解决线性优化问题，也是NP难问题。然而，文献[7]已经证明获得的解决方案由L0范数最小化可以等价于求解L1范数的最小化。SRC在人脸识别和鲁棒性方面表现非常好，虽然SRC已经极大地影响人脸识别领域并且被广泛地使用和研究，但还有一些未解决的问题。例如，它不能完美地解决人脸姿态变化、照明条件和面部表情等因素的影响。而且SRC算法通常是迭代求解最小化问题，因此耗时很长。目前已经有人提出很多方法改进SRC算法来获得更好的性能。例如，邓等人[8]提出了一个扩展的SRC，该方案是应用了一个内部变体字典来表示训练样本和测试样本之间的差异。He等人[9]提出了一个两阶段测试样本稀疏表示方法来提高数据集的健壮性和算法的效率。所有的这些方法仍然忽略了一个非常重要的事实，那就是训练样本仍不能精确地表示测试样本且噪声不能直接丢弃。传统的SRC方法都是假设每个测试样本可以用训练样本线性地表示。这个假设很难避免噪声问题，并且在样本的个数大于训练样本个数时，不能精确地表示测试样本。

基于上述描述，我们提出利用局部线性编码的方法和在迭代降噪处理的过程中考虑类依赖的特性，构建一个能够揭示数据局部结构和样本之间类依赖关系的方法，来提升在噪声条件下SRC的分类效果。我们的假设是通过选择训练样本的子集作为局部字典，并用其线性表示测试样本，能够很好地提高SRC算法的时间复杂度，也有过滤部分噪声的效果。

1 相关研究

假设有n个训练样本，用向量的形式表示为X=[x1,x2,x3,…,xn]，其中总共有C类，每个类别有m个样本。所有的测试样本用y表示，在操作之前应该将所有样本归一化为长度为1的单位列向量。

1.1 SRC

当谈到基于L1范数优化的表示分类方法时，稀疏表示（SRC）是最具有代表性的方法。它是使用训练样本确定一个线性组合来表示测试样本y。因此，SRC可以大致用下面的式子来表示：

其中y是归一化之后的测试样本，xi的系数表示为ai(i=1,2,…,n)。为了便于描述我们可以按下列的方式重写（1）式。

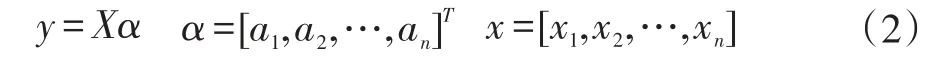
可以使用L1范数来求解α的最小化问题：

或者：

或者：

我们利用拉格朗日算法来求解式（5），其中α是训练样本矩阵X的系数。λ作为拉格朗日乘子。ξ是一个小的实数。

1.2 迭代降噪处理

据研究所知，式（2）不能准确地表示真实情况下训练样本和测试样本之间的关系，我们可以确定的是来自任何主体的脸部图像都有不可预知的组成部分和表示噪声。这里迭代处理NMFIRC的主要原理是：迭代计算线性组合系数的表示解和表示噪声，直到它收敛，然后利用确定的“最优”表示解决方案来分类。对于（1）式中的si可以表示噪声，也可以用下面的式子表示：

其中si表示噪声向量，同样地可以用基于L1范数的优化问题来求解α。如下所示：

这里假设样本数据已经做了归一化处理，D表示处理之后的数据。首先设y′=y-si我们可以通过如下式子来求解α的值：

该式子等价于求解：

并计算然后设则目标函数可以表示为：

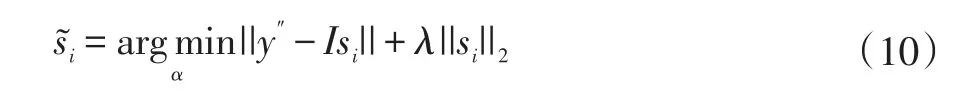
同样地，我们可以通过以下式子求解：

反复执行（8）（10）两步更新si，直到最大迭代次数为止。

2 提出的相关方法

本节将详细的讲解我们所提出的方法，不管是基于L1范数的稀疏表示分类算法（SRC）或者是基于L2范数的协作表示（CRC），这些方法都是假设每个测试样本可以由训练样本线性表示，不过这个假设忽略了一个非常重要的事实，那就是测试样本依然不能用训练样本精确的表示，例如噪声不能直接被丢弃。因此，我们提出的假设是在选择字典集时来表示测试样本时，是否可以有选择的丢弃部分噪声数据，以达到更精确地线性表示组合。同时，传统的SRC的一个限制是它不包含数据集的类标签（先前）信息。它只使用类标签信息在计算每个类的残差时进行后处理，却忽略了类之间欧几里得距离的相关性。我们提出类依赖的KNN方法，将获得的距离信息和传统的分类信息统一起来，以达到更好的分类效果。

2.1 局部线性编码设计

由LCC[10]可得，局部特征比稀疏性更为重要，局部必然会导致稀疏性，反之亦然。我们提出的方法通过选择局部约束来达到更好的稀疏性。在流形学习中，局部线性被用来捕捉局部的几何结构。例如，局部线性嵌入（LLE），使用局部邻居线性重建每个数据，目的是捕捉自然的局部结构。我们首先在原始的训练样本中选择它的K个最近邻样本，作为子集字典。解决以下式子来求解最优化问题：

其中样本xi的K最近邻居表示为：

λ＞0是平衡因子，通过循环迭代（8）（10）（11）式子以达到最优化的稀疏向量表，即为数据对象xi的最佳稀疏重构系数。该系数表示为：

我们可以通过图1更直观地表示。

2.2 类依赖KNN（cdKNN）

SRC分类算法主要是通过比较每类的残差来确定测试样本的类别，没有考虑样本的空间距离信息，在各种各样的文献中，例如SOMAP，局部线性嵌入，局部保留投影（LPP）和局部Fisher判别分析（LFDA），都是考虑了样本之间的局部结构信息。研究表明，LFDA提供了一个很好的方法将数据投影到较低维的子空间。使得来自不同类的样本被很好地分离，另外LFDA通过保留每各类的局部结构得到有效的组合实现了线性判别分析和LPP的性质。受到这些启发，我们引入cd⁃KNN来捕获样本之间的局部结构，通过融合残差信息和样本之间的欧几里得距离信息达到更优的分类效果。

2.3 基于局部线性编码和融合局部结构信息的SRC优化算法

假设训练数据集用表示，每个类别中的数据用表示，测试样本为y∈Rd，则整个流程如下：

第一步：对所有的训练样本和测试样本使用PCA方法，得到P∈Rd×p的投影矩阵，并通过计算D=PTX得到p维的数据集用D表示。

第二步：在降维后的数据集D之上选择局部线性编码样本。主要是通过KNN算法选择与测试样本相近的K个样本作为局部字典集。用XN(xi)表示。

第三步：对选择的局部训练样本和测试样本用如下方法进行归一化，XN(xij)=XN(xij)/||XN(xij)||和y=y/||y||，并且用si=[0,0,....,0]T表示初始噪声。

第四步：反复执行式子（9）（10）（11）直到最大迭代次数q为止，更新和的值。

第五步：计算每个类别的残差，使用如下式子，即第i类的残差：

其中XN(xij)是第i类，第j个训练样本。第i类的样本个数为第二步选择的k个最近邻居，则是预先计算得到的最佳稀疏系数。

第六步：计算测试样本y和第二步求得的样本字典集中每个样本XN(xij)的欧几里得距离，即dij=D(y,XN(xij))。并求其平均距离作为第i类的距离。

第七步：求得以下式子即为测试样本y的类别标签。

图1 即为提出的局部线性编码的整个流程

3 实验与结果分析

3.1 实验数据集

在图像识别领域，最常用的数据集有三个，分别是ORL人脸数据库、PIE数据库和AR数据库。实验中使用这三种人脸数据来验证我们的想法。其中ORL数据库包含40个类别，每类10个样本的图像。每幅图像的面部表情和外部特种都各部相同。实验数据是从每类中选择5幅图像作为训练数据，共200幅，其他图像作为测试数据。AR图像数据主要在脸部表情上存在较大的变化，实验中，选择了20个类别，每类10幅图像，其中选择每类5幅作为训练数据，5幅作为测试数据。PIE数据集的特点是每个人采集时的光照、表情和姿态都不一样，同样是选择其中20个类别，每个类别21幅。实验中每类选取17张作为训练数据，4张作为测试数据。

3.2 实验结果分析

我们的算法主要是通过利用局部线性编码的方式过滤掉部分噪音数据和融合具有类依赖特性的空间距离信息来提高分类精度。因此，实验中，分别验证这两种方法对SRC分类效果的影响，并且最终与我们的算法效果作对比来验证我们提出方法的有效性。表1显示的是不同算法在三种数据集上的最优识别率。其中cdSRC算法的参数包括融合稀疏（p）即最优权重，LLC+SRC方法是选择合适的局部字典集，参数为选择字典集的个数（K），而我们的算法（cdLLCSRC）是包括的参数有：选择局部编码集的个数（K），融合空间距离信息的参数（p），和降噪过程中的迭代次数（t）。

表1 几种算法最优识别率比较（%）

从实验结果中可以看出：（1）在三种数据集上我们的算法和基本的SRC算法、有类依赖特性的SRC算法（cdSRC）、从LLC算法借鉴过来的LLCSRC算法相比较，都取得了更好的分类结果。（2）其中类依赖的SRC（cdSRC）算法在特定的条件下相比SRC算法有优异的结果；而根据LLE算法思想改进的SRC算法比SRC算法也有很好的表现。通过对比发现，我们的算法分类效果优异且得到了很大的提升，这充分证明脸表情、光照、角度的影响下，cdSRC和LLCSRC的表现不佳。主要是因为在含噪声的图像中，选取的图像特征量的多少对分类效果有较大的影响。我们融合了LLC思想和类依赖的特性得到的cdLLCSRC算法却在少量特征条件下得到了很好的分类效果。这也充分表明了我们算法的有效性。

图2是各个算法在三种不同的数据集上的识别率表现，可以发现在人脸表情、光照、角度的影响下，cd⁃SRC和LLCSRC的表现不佳。主要是因为在含噪声的图像中，选取的图像特征量的多少对分类效果有较大的影响。我们融合了LLC思想和类依赖的特性得到的cdLLCSRC算法却在很少的特征条件下得到了很好的分类效果。这也充分证明了我们算法的有效性。

图2

图3

图4

4 结语

本文提出了选择局部编码并融合欧几里得距离信息来提升在噪声条件下对人脸图像的分类效果。实验表明我们的方法在低维条件下也能取得很好的分类效果。当然，我们的算法涉及选择局部编码个数的参数K和权衡距离信息的平衡因子p。如何降低调参的复杂度，将是我们未来探索的方向。

[1]M.Elad,M.Aharon,Image Denoising Via Sparse and Redundant Representations Overlearned Dictionaries,IEEE Trans.Image Process，2006，15（12）：3736-3745.

[2]J.Mairal,M.Elad,G.Sapiro,Sparse Representation for Color Image Restoration,IEEE Trans.Image Process，2008，17（1）：53-69.

[3]T.Bai,Y.F.Li.Robust Visual Tracking with Structured Sparse Representation Appearance Model,Pattern Recognit，2012，45（6）：2390-2404.

[4]X.Zhu,J.Liu,J.Wang,C.Li,H.Lu.Sparse Representation for Robust Abnormality Detection in Crowded Scenes,Pattern Recognit，2014，47（5）：1791-1799.

[5]L.-C.Chen,J.-W.Hsieh,Y.Yan,D.-Y.Chen,Vehicle Make and Model Recognition Using Sparse Representation and Symmetrical Surfs,Pattern Recognit，2015，48（6）：1979-1998.

[6]J.A.Wright,A.Y.Yang,A.Ganesh,S.S.Sastry,Y.Ma.Robust Face Recognition Via Sparse Representation,IEEE Trans.Pattern Anal.Mach.Intell，2009，31（2）.

[7]K.Yu,T.Zhang,Y.Gong.Nonlinear Learning Using Local Coordinate Coding.Proc.of Nips'09,2009.

[8]W.Deng,J.Hu,J.Guo,Extended SRC:Undersea Mpled Face Recognition Via Intraclass Variant Dictionary,IEEE Trans.Pattern Anal.Mach.Intell，2012，34（9）：1864-1870.

[9]S.T.Roweis,L.K.Saul.Nonlinear Dimensionality Reduction by Locally Linear Embedding,Science，2000，290（5500）：2323-2326.

[10]E.Candes,T.Tao.Near-Optimal Signal Recoveryfrom Random Projections:Universal Encoding Strategie.