Effects of ply orientation and material on the ballistic impact behavior of multilayer plain-weave aramid fabric targets

Gaurav Nilakantan,Steven Nutt

Mork Family Department of Chemical Engineering and Materials Science,M.C.Gill Composites Center,University of Southern California,Los Angeles,CA 90089,USA

1.Introduction

Continuous- filament woven fabrics comprised of high strength and high stiffness para-aramid materials such as Kevlar®(DuPont)and Twaron®(Teijin)are commonly used in law enforcement and military body armor to provide ballistic and blast protection to the torso and extremities[1-5].The impact performance of woven fabric or textile structures used in body armor is contingent on intrinsic and extrinsic factors.Extrinsic factors include the testing configuration,testing methodology,and projectile characteristics.Intrinsic factors include the geometrical,material,and architectural properties of the textile structure.Understanding the sensitivity of the ballistic impact performance to these factors is critical to designing lightweight body armor structures optimized for protection.Virtual testing through computational simulation(e.g.finite element analysis)has gained increasing momentum over the past decade,and while it is notyet ready to fully replace destructive experimental testing,it is fast gaining traction as a tool to quickly and efficiently explore new materials,weaves,and architectures through parametric studies as well as to identify and understand various mechanisms of deformation,failure,and energy dissipation that cannot be easily elucidated through experimental means.Such insight can be used to initially down-select candidate weave and material combinations from the extremely large material architecture design space available for body armor;that would otherwise be prohibitively expensive to manufacture and experimentally test each design iteration.

Advancements in multiscale modeling techniques have made possible the simulation of realistic-sized textile structures across the continuum length scales from the fiber to the fabric level.Barauskas and Abraitiene[6]were the first to present a multiscale modeling approach for woven fabrics that explicitly incorporated two length scales(i.e.yarn,fabric)within the same finite element model using a single finite element formulation(i.e.2D shell element).Since then,other multiscale models[7-15]have also incorporated multiple length scales(e.g. fiber,yarn,fabric)using multiple finite element formulations(e.g.1D truss element,2D shell element,3D solid element)within the same finite element model;including fiber-level modeling of single yarns[14,16-18]and fiber-level modeling of the entire fabric[13,19-21].Advancements in probabilistic modeling techniques have made possible the incorporation of experimentally-observed sources of statistical variability into the finite element simulations thereby enabling the vital transition from the deterministic-only capability of virtual testing to now predicting the probabilistic penetration performance of armor systems[22].Nilakantan et al.[23]was the first to introduce a new class of probabilistic simulations of woven fabric impact wherein sources of geometric and material statistical variability were mapped into the fabric finite element model.Then,through a series of impact simulations at varying impact velocities,each with a unique set of mappings,a numericalV0-V100curve was generated to represent the probability of complete fabric penetration(ranging from 0 to 1)as a function of projectile impact velocity(V).This probabilistic computational framework was capable of capturing the experimentally-observed zone of mixed results(ZMR),wherein certain penetrating shots could have an impact velocity lower than certain non-penetrating shots.This framework was then used by Nilakantan et al.[24-26]to study the stochastic effects of yarn strength,yarn friction,and projectile characteristics on theV0-V100curve of partially and fully clamped single-layer Kevlar fabric targets.This framework was later adapted by Wang et al.[19]to study the effect of inter- fiber friction on theV0-V100curve for a single-layer Kevlar fabric target.

The literature[1-4]is replete with deterministic numerical studies of fabric impact that utilize 3D yarn-level finite element models.The majority of these deterministic studies utilize singlelayer fabric models and primarily focus on the effects of interyarn friction,such as Duan et al.[27]and Nilakantan et al.[26].Some attempts[28,29]have been made at modeling deterministic multi-layer fabric targets at the 3D yarn-level.For example,Jia et al.[28]studied the impact response of 3D orthogonal weave Twaron fabrics and Chocron et al.[29]studied the impact response of multi-layered Kevlar fabrics.There are few deterministic studies that have parametrically investigated the effects of yarn material,fabric weave,and textile architecture on the ballistic impact performance of woven fabrics[30-33],and even fewer still that have considered such parametric effects on multi-layered fabric targets.For example,Tran et al.[33]studied the single-layer impact response of plain weave,basket weave,and knitted Twaron fabrics,considering various projectile shapes.Erol et al.[34]studied the inplane tensile and shear responses of single-layer plain,basket,twill,and satin weave architectures.Nilakantan et al.[31,32]studied the single and multi-layer impact response of unstitched and stitched 2D plain weave fabrics,as well as 3D fabrics comprised of unidirectional warp and fill tows interlaced by Z-tows of various inclinations and depths.Rao et al.[30]studied the effects of yarn stiffness and strength on the single-layer impact response of a plain weave Kevlar fabric.Ha-Minh et al.[35]studied the effect of friction on the impact response of 3D orthogonal weave Kevlar fabrics.In addition to weave architecture and material,there are other important practical factors to consider such as the projectile characteristics,target size and shape,and boundary or clamping configurations as these factors will undoubtedly also affect the fabric impact response.Examples of such studies,once again utilizing 3D yarn-level models,include Nilakantan and Nutt[36,37],Zhang et al.[38],and Nilakantan et al.[39].

Egres et al.[40]and Nilakantan et al.[41]disclosed inventions for new,innovative fabric target constructions based on ‘sheared’or‘non-orthogonal’plain-weave fabric architectures wherein the warp-to- fill yarn angle was lowered below the conventional 90°(e.g.15°-75°).In addition,each ply of the multilayer fabric target were rotated relative to each other.Both works demonstrated the improved ballistic impact performance in terms of reduced backface signature(BFS)of such architecturally-modified fabric targets while keeping the same yarn material.Thus,it is not simply a matter of using stiffer and stronger yarns,but also the particular manner in which the yarns and woven plies are constituted within the fabric target.BFS is an important performance metric because of the likelihood of behind armor blunt trauma(BABT)that can cause severe internal injuries.Forexample,the NIJ0101.06 standard[42]prescribes a maximum BFS of 44mm for at least 80%of the test shots and a maximum limit of 50 mm that should not be exceeded.

The present numerical study focuses on architectural and material effects on the ballistic impact response of a multi-layered Kevlar fabric target using two clamping configurations.The first part of the study focuses on the effects of individual ply orientation by considering various ply layup configurations along with three levels of inter-yarn friction.The second part of the study focusses on functionally grading the yarn material properties through the target thickness by varying the yarn tensile stiffness and strength in each ply.The effects of precise projectile impact location relative to the principal yarns and incorporating the nesting of fabric plies in the numerical model are also discussed.All simulations are performed using LS-DYNA.For each target configuration and impact scenario,two projectile impact velocities(Vi)are considered,one non-penetrating and one penetrating.Note that in some cases the non-penetrating test shots can result in the failure of individual fabric plies with the exception of the last ply that always remains intact.Because only deterministic models are considered,fabric impact performance is assessed by the time taken to arrest the projectile and the peak dynamic deflection(or BFS)for the nonpenetrating impact tests,and by the residual projectile velocity(Vr)for the penetrating impact tests.

2.Methodology

2.1.Material

A plain weave aramid fabric(Kevlar S706)is used in this study.The areal density of the fabric is 180 g/m2with an approximate thickness of 0.23mm.The warp and fill yarns are 600 denier yarns(Kevlar KM2)with a yarn span of 0.747mm.Eachyarn is comprised of 400 approximately circular filaments of diameter 12μm and density 1.44g/cm3.The longitudinal yarn tensile modulus is 82.6GPa with a tensile strength of 3.4 GPa.

2.2.Target configuration

All fabric targets consist of 6 unstitched plies of in-plane dimensions 76.2 mm×76.2mm.Fig.1 displays the impact test setup.Two clamping configurations are considered for each fabric targeta fully clamped(i.e.4-sided)and a partially clamped(i.e.2-sided)configuration.These particular choices of target in-plane size and target clamping configuration in this study were purposefully made to be consistent with other deterministic fabric models reported in the literature[1-3]that often consider single-layer,square-and rectangular-shaped,2-and 4-sided clamped fabric targets of inplane sides between 25.4mm and 101.6 mm in length.Five target configurations(see Table 1)are considered based on the individual ply orientations as follows(configuration#-angles):(#1-0°,0°,0°,0°,0°,0°),(#2-+45°,-45°,+45°,-45°,+45°,-45°),(#3-0°,+15°,-15°,+45°,-45°,0°),(#4-0°,+45°,0°,+45°,0°,+45°),and(#5-+15°,+30°,+45°,-45°,-30°,-15°).Fig.2 displays a schematic of the various ply orientations,warp yarns are colored in red and fill yarns in yellow.The ply angle refers to the angle made by the warpyarns with the horizontal or+X axis.Because the warp and fill yarns are modeled with the same crimp in the finite element model,a+45°ply is the same as a-45°ply.Two functionally graded target configurations are considered based on six hypothetical yarn material choices,for which the range of properties(i.e.yarn tensile moduli and strength)are within the realm of existing Kevlar and Twaron yarns[43,44].For the first functionally graded target configuration,#A,the yarn tensile moduli progressively increase from the top ply(strike face)to the bottom ply(rear face),while in#B,they progressively decrease.Fig.3 displays the tensile stress-strain constitutive relationships for each of the six yarn materials used in the fabric model,with a longitudinal tensile modulus as follows(material#-Young's modulus in GPa):(#1-99.1),(#2-92.5),(#3-85.9),(#4-79.3),(#5-72.7),and(#6-66.1).The stress-strain curves represent a linear elastic material until failure in accordance with observations from experimental single-yarn tensile testing[45].For each of these six hypothetical yarn materials,the total strain energy density was purposefully kept constant to allow for a consistent comparison to be made between each other.Thus,as the yarn tensile modulus increases,the tensile strength correspondingly decreases,however the total energy required to fail the yarn remains constant.The range of yarn tensile modulus values considered in this study was obtained by considering a±20%variation in the baseline yarn tensile modulus of 82.6GPa,which is the reported experimental value for a 600-denier Kevlar KM2 yarn[44].The actual yarn tensile modulus in a woven fabric can be varied by either choosing a different underlying fiber type(e.g.for Kevlar:29,49,129,KM2,etc.)or a different yarn denier(e.g.600,850,1000,etc.)based on the number of single fibers within the bundle.For example,Kim et al.[44]report an experimental yarn tensile modulus range of 73.7-120 GPa for various Kevlar yarn constructions.

Table 1Fabric ply orientations within each target configuration.

2.3.Impact testing

A 0.22 caliber spherical steel projectile of mass 0.692 gm and diameter 5.556 mm impacts the fabric target once at its center,as shown in Fig.1.This projectile type has been widely utilized in the literature for experimental and numerical fabric impact studies[1-3].The projectile is considered to be non-deformable in the simulations for consistency.Only for target configuration#1,two projectile impact locations are separately considered where the projectile either directly impacts a yarn cross-over location(yarn impact,i.e.,configuration 1a)or the interstitial gap between four yarns(gap impact,i.e.,configuration 1b).Here,all six 0°plies are perfectly aligned with each other.To study the effect of ply nesting,an additional configuration(i.e.,configuration 1c)is considered wherein all even-numbered plies in target configuration#1 are translated horizontally along the warp and fill yarn directions by half a yarn span,as shown in Fig.4.Two projectile impact velocities are considered-one non-penetrating velocity of 200m/s,and one penetrating velocity of 300m/s.For the non-penetrating test shots,some of the fabric targets may experience individual ply failure of the top plies,although the last ply will always remain intact,and the projectile will never exit through the target.The residual projectile velocity(Vr)is considered zero for non-penetrating shots.The ballistic impact performance metric for non-penetrating shots is assessed by the backface signature or peak fabric dynamic deflection,as well as the time taken to completely arrest the projectile(i.e.,zeroVr),while the magnitude ofVris used as a metric for the penetrating shots.

2.4.Finite element model

The individual Kevlar yarns are explicitly modeled as homogenous continua and discretized with single integration point solid elements.Both the warp and fill yarns are assumed to have the same degree of undulation or crimp.To account for the homogenization of the actual fiber-level yarn architecture,the material properties must be adjusted by the fiber packing fractionνf,which is computed as the ratio of the actual fiber cross-sectional area to the cross-sectional area of the homogenized finite element yarn,resulting in aνfvalue of 87%.The yarns are assigned a transversely isotropic material model with the following adjusted properties:Eaxialof 71.85 GPa(E11),Etransof 7.18GPa(E22,E33),Gof 718.5 MPa(G12,G23,G31),ν of 0.0(ν12,ν23,ν31),and ρyarnof 1.25g/cm3.For the functionally graded targets,anEtransof 1/10th and aGof 1/100ththe respectiveEaxialvalues are used.A coefficient of friction(μPF)of 0.23 is used between the projectile and the fabric.Three levels of inter-yarn friction(μy-y)are considered:a low,a baseline,and a high case with respective values of 0.10,0.18,and 0.3.The baseline friction coefficient is representative of experimentally reported values for Kevlar[30,46,47].Then,the lower and upper range of yarn friction coefficients would be respectively representative of a lubricated yarn(e.g.coated fiber surface)and a scoured yarn(e.g.removed sizing,roughened fiber surface).Obviously,the inter-layer friction coefficient(i.e.friction between the yarns of two adjacent layers)is the same as the inter-yarn friction coefficient.An element erosion-based failure model is used based on a maximum tensile stress failure criterion(σfail)of 3.4GPa,which after adjusting by the filament packing fraction of 87%to account for the homogenized yarn becomes 2.95GPa.A zero-slippage or perfectly clamped boundary condition is modeled by constraining all the degrees of freedom of the fabric nodes that are within the upper and lower fixture plates.The finite element code LS-DYNA is used for all impact simulations.

Fig.2.Fabric ply orientations(warp yarns-red, fill yarns-yellow).Note:positive angles refer to counter-clockwise ply rotations.

Fig.3.Yarn tensile stress-strain plots for the functionally graded fabric targets.

3.Results and discussion

3.1.0°and ±45°oriented fabric targets

Fig.4.Projectile impact locations relative to the principal yarns for Configuration 1.

This section compares the impact behavior of the Config 1a(all 0°plies)and Config 2(±45°plies)fabric targets for 4-sided and 2-sided clamping configurations at aVi of 200 m/s and 300 m/s,which respectively correspond to non-penetrating and penetrating impact velocities.Fig.5 compares the projectile velocity histories of Config 1a and Config 2 for the two impact velocities and two clamping configurations.Fig.5(a)shows the 4-sided clamped targets arrest the projectile faster than their 2-sided clamped counterparts for both Config 1a and Config 2 at aVi of 200 m/s.Note that the 2-sided clamped targets do not exhibit any yarn failure at the time of projectile arrest,whereas the 4-sided clamped targets exhibit varying extents of ply penetration wherein yarn failure initiates in the strike face( first ply)around 30μs for Config 1a and 35μs for Config 2.Fig.6 shows that for the 4-sided clamped targets at the time instant of projectile arrest(i.e.,zeroVr),Config 1a has five penetrated plies,while only the first three plies have been penetrated by the projectile in Config 2.Thus,for even slower nonpenetrating impact velocities wherein no yarn failure is encountered for the 4-sided clamped targets,it is expected that the time taken to arrest the projectile will be significantly less than the 2-sided clamped targets.Fig.5(a)also shows that Config 2 targets arrest the projectile faster than Config 1a targets for both clamping configurations.

Fig.5.Projectile velocity histories for the 4-and 2-sided clamped Configuration 1a and Configuration 2 fabric targets at a Vi of(a)200 m/s(b)300 m/s.

Fig.7 displays perspective views of the fabric deformation state at the time instant of projectile arrest for the 4-sided clamped Config 1a and Config 2 targets at aVi of 200 m/s.At the time of projectile arrest,the transverse displacement wave has reached the clamped boundaries for Config 1a and the base of the pyramidal fabric deformation volume is diamond-shaped.In comparison,at the time of projectile arrest for Config 2,the transverse displacement wave has not reached the clamped boundaries and the base of the pyramidal deformation is square-shaped.This shape is a consequence of the ±45°ply orientations relative to the clamped boundaries.For the penetrating impacts at aVi of 300 m/s,Fig.5(b)shows that the 2-sided clamped targets result in a lowerVr than their 4-sided clamped counterparts for both Config 1a and Config 2.Fig.5(b)also shows that for each clamping configuration,Config 2 targets result in a lowerVr than Config 1a.Overall,Config 2 exhibits superior impact performance relative to Config 1a for the two impact velocities selected.

Fig.8 displays the fabric energy transformation histories during the impact event for the 4-and 2-sided clamped Config 1a targets at aVi of 300m/s.The time instant of deviation in the fabric internal and kinetic energies,at～15μs,corresponds to the instant of yarn failure in the strike face of the 4-sided clamped target.The fabric kinetic energy,an indication of the extent of momentum transfer between the projectile and target,grows at a faster rate to much higher overall levels than the fabric internal energy,which is indicative of tensile yarn straining.The frictional or sliding energy dissipated by frictional interactions between the warp and fill yarns in each layer as well as inter-layer interactions,steadily grows at similar rates and magnitudes for both the 4-sided and 2-sided clamped targets.Moreover,the fabric frictional energy initially grows at slower rates than the fabric internal energies for both clamping configurations.However,the magnitude of frictional energy catches up and even overtakes the fabric internal energy towards the end of the impact event,i.e.,around the start of the plateau region of the projectile velocity history that indicates almost complete target penetration.

Fig.9 displays fabric energy transformation histories for the 2-sided clamped Config 1a and Config 2 targets at aVi of 300 m/s.Similar trends are observed with the fabric kinetic energies dominating the overall energy dissipation,and the fabric frictional energies growing at lower initial rates than the fabric internal energies.However,the frictional energy continuously grows during the impact event and eventually overtakes the fabric internal energies in magnitude.Figs.8 and 9 indicate that the delayed onset of ply failure in the strike face as well as subsequent plies results in the lowerVr of the 2-sided clamped targets compare to the 4-sided clamped targets,as well as the lowerVr of the Config 2 targets compare to Config 1a.This is further attributed to the greater extents of momentum transfer that continuously occur between the projectile and fabric target while the plies remain intact.However,once the plies fail,their contribution to the overall fabric kinetic energy greatly diminishes,keeping in mind that this penetrating impact event is dominated by the fabric kinetic energy and governed to much lesser extents by the fabric internal and frictional energies.

The similarity in magnitudes of frictional energies for all four cases is unusual and indicates similar extents of frictional sliding perhaps brought about by the decreased yarn mobility within each ply caused by the pressing together of multiple plies.This is distinct from single-layer fabric targets,wherein large differences are seen in the frictional energies of 2-sided clamped normal and bias oriented targets as well as in normal oriented 2-sided and 4-sided clamped targets.For such impact scenarios,yarn reorientation(or scissoring)and principal yarn pullout are predominant frictional energy dissipating mechanisms.Such mechanisms appear to be suppressed in these multilayer fabric targets.However,these penetrating impact events occurred over relatively short time scales(maximum of 50μs)that were momentum-driven.In contrast,for longer time scales,larger fabric targets,and impact velocities closer to the respective fabricV50velocities,frictional energy dissipating mechanisms may have greater opportunity to manifest.

Fig.10 compares the 4-sided and 2-sided clamped fabric ply deformation states at select time intervals for the first layer(strike face)and sixth layer(rear face)for Config 1a targets at aVi of 300m/s.At 20μs,both projectile velocity histories are still overlapping,as shown previously in Fig.5(b).At this time instant,the failure pattern in the first layer appears similar for both the 4-sided and 2-sided targets,with only a few warp yarns(in red)and a few fill yarns(in yellow)failed at the impact site,as shown in Fig.10.However,later,as the projectile velocity histories start to deviate from each other,as shown in Fig.5(b),the yarn failure patterns in the rear face appear different for the 4-sided and 2-sided clamped targets(see Fig.10).The exit hole in the sixth layer of the 4-sided clamped target appears circular,with a similar number of warp and fill yarns failing in tension.In contrast,the exit hole is oblong for the 2-sided clamped target,with a greater number of failed warp yarns compared to failed fill yarns.Recall that in these 2-sided clamped Config 1a targets,the fill yarns are unclamped,while the warp yarns are clamped,leading to higher warp yarn tension levels during impact and a greater number of warp yarn failures.However,once a few of the unclamped principal fill yarns have failed at the impact site,the neighboring fill yarns simply slide around the penetrating projectile,remaining intact and leading to a windowing mechanism and the oblong exit hole.

Fig.11 compares the side view of fabric deformation and ply failure at specific time intervals for the 4-sided clamped Config 1a targets at a non-penetratingVi of 200 m/s and a penetratingVi of 300m/s.The black arrows in Fig.11 mark the fronts of the outwardly propagating transverse displacement wave.The fabric material behind the transverse wave front and within the pyramidal deformation volume contribute primarily to momentum transfer between the projectile and fabric target.At the time of projectile arrest,only the sixth layer(rear face)remains intact,as shown in Fig.11(a)for the non-penetrating shot.As the first five fabric layers progressively fail,individual layers start to spring back and separate from the rest of the fabric target,as the plies are not stitched together.Similar behavior is shown in Fig.11(b)for the penetrating shot,although all fabric layers have failed.At the instant of complete projectile penetration through the fabric target,the transverse displacement wave fronts remain well away from the clamped boundaries.Thus,the impact event is localized within the interior of the fabric target.

Figs.12-14 compare the fabric deformation states at specific time intervals between 2-sided clamped Config 1a and Config 2 targets at aVi of 200 m/s.Recall for these 2-sided clamped nonpenetrating shots,there is no yarn failure during the impact event.Fig.12 displays a perspective view of fabric deformation,clearly showing the pyramidal fabric deformation and the fronts of the transverse displacement wave,while Fig.14 displays the corresponding side views.The base of the pyramidal deformation is diamond-shaped for Config 1a,and is wider along the warp yarn direction,since the warp yarns are clamped,while the fill yarns are unclamped.At the time of projectile arrest,the transverse displacement wave has reached the clamped boundaries,although it has not reached the free edges of the fabric target.In comparison,the base of the pyramidal deformation is square-shaped for Config 2,where the warp and fill yarns are at±45°relative to the clamped boundaries,thus,at least one end of both the warp and fill yarns are clamped.At the time of projectile arrest for the Config 2 target,the transverse displacement wave has not reached the fabric boundaries.

Fig.6.Individual fabric ply deformation states at the time instant of projectile arrest for 4-sided clamped targets at a Vi of 200m/s(a)Configuration 1a at 100μs(b)Configuration 2 at 75μs.

Fig.13 displays the contours of vertical fabric displacement along the direction of projectile travel.These color contours clearly distinguish the propagation of the transverse displacement wave,and the shape and size of the base of the pyramidal deformation.For single-layer 2-sided clamped fabric targets,the two free edges of the fabric are typically pulled inwards towards the impact site.However,for these multi-layer targets,there appears to be only minimal inward pulling of the free edges towards the impact site,a consequence of the inter-ply friction that limits the mobility of each layer.

Fig.7.Fabric deformation states at the time instant of projectile arrest for 4-sided clamped targets at a Vi of 200 m/s(a)Configuration 1a at 100μs(b)Configuration 2 at 75μs.

Fig.8.Energy transformation histories for the 4-and 2-sided clamped Configuration 1a fabric targets at a Vi of 300 m/s(IE-internal energy,KE-kinetic energy,FE-frictional energy).

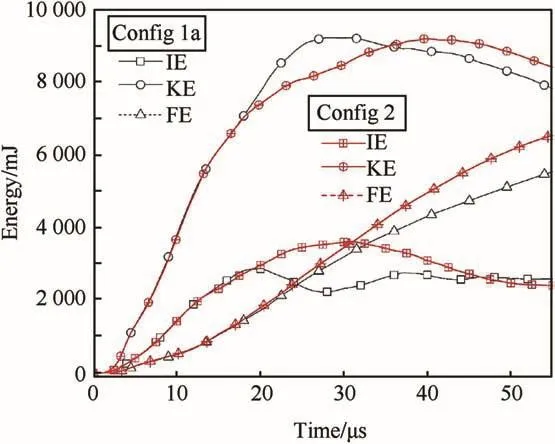
Fig.9.Energy transformation histories for the 2-sided clamped Configuration 1a and Configuration 2 targets at a Vi of 300 m/s(IE-internal energy,KE-kinetic energy,FE-frictional energy).

3.2.Effects of ply orientation,stacking sequence,and inter-yarn friction

This section compares the impact performance of the five fabric target configurations(Config 1 to Config 5)that consist of various ply orientations.Both 2-sided and 4-sided clamped configurations are considered with the same two choices of projectile impact velocity-non-penetrating at aVi of 200 m/s,and penetrating at aVi of 300m/s.In addition,three inter-yarn friction levels(μy-y)of 0.10,0.18,and 0.30 are considered.Fig.15(a)and(b)respectively display the time required to arrest the projectile,and the corresponding peak fabric dynamic deflection at the time of arrest for the 4-sided clamped fabric targets at aVi of 200m/s.For Config 1a,Config 2,and Config 5,increasing levels of inter-yarn friction result in increasing peak fabric dynamic deflections and increasing times to arrest the projectile.However,Config 3 and Config 4 exhibited distinct and unexpected trends.The lowest fabric dynamic deflection and corresponding fastest time to completely arrest the projectile were observed for Config 2 with aμy-yof 0.10.For the penetrating impacts at aVi of 300 m/s in all five configurations,the lowestμy-yof 0.10 resulted in the lowest residual velocities,while the highestμy-yof 0.30 resulted in the highest residual velocities.In Config 1a,the two lowestμy-ylevels resulted in an identical residual velocity,while for Config 4 and Config 5,the two highestμy-ylevels resulted in identical residual velocities.These trends clearly indicate that the effects of inter-yarn friction for both non-penetrating and penetrating impact events are closely tied to the architecture of the fabric target,which in this case is the ply orientation.Comparing all fabric target configurations and cases,Config 2 with aμy-yof 0.10 resulted in the highest overall impact performance.

Fig.16 displays information analogous to Fig.15,but for the 2-sided clamped targets.As shown in Fig.16(a)and(b),for Config 1a with aVi of 200 m/s,the three inter-yarn friction levels result in the exact same peak fabric dynamic deflection,but take different times to arrest the projectile.Apart from Config 1 and Config 5,higher inter-yarn friction levels resulted in shorter times to arrest the projectile and smaller peak fabric dynamic deflections.Config 3 showed insensitivity to inter-yarn friction for the non-penetrating impact,with allthree μy-ylevels yielding similar metrics.Fig.16(c)shows that for the penetrating impact at aVi of 300 m/s,increasing inter-yarn friction levels leads to increasing residual velocities.Thus,the trend in residual velocities and inter-yarn friction levels is similar for both the 4-sided and 2-sided clamped fabric targets across all configurations.Comparing all fabric target configurations and cases,Config 2 with aμy-yof 0.30 resulted in the highest non-penetrating impact performance,while Config 2 with aμy-yof 0.10 resulted in the highest penetrating impact performance.A general observation from this deterministic study and for this impact scenario is that a bias-oriented,fully-clamped or partially-clamped multi-layer fabric target with a low level of interyarn friction yields improved impact performance.

Fig.10.Individual fabric ply deformation states for Configuration 1a fabric targets at a Viof 300 m/s(left)4-sided(right)2-sided.

Fig.11.Side view of fabric deformation states for 4-sided clamped Configuration 1a at a Viof(a)200 m/s(b)300 m/s.

Fig.12.Fabric deformation states for 2-sided clamped targets at a Viof 200 m/s(left)Configuration 1a(right)Configuration 2.

Fig.17 compares the non-penetrating and penetrating impact performance metrics of the 2-sided and 4-sided clamped fabric targets for all configurations with a baselineμy-yof 0.18.In addition to Config 1a that consisted of aligned fabric plies with a yarn-based impact location,Config 1b and Config 1c are also included,where the former consists of aligned fabric plies with a gap-based impact location and the latter consists of nestled fabric plies with a yarnbased impact location.To recall,yarn and gap impacts refer to the precise location of impact of the projectile at the fabric dead center.Fig.17(a)and(b)show that for Config 1,the non-penetrating impact response is sensitive to the precise location of projectile impact and the layer-to-layer alignment for the 4-sided clamped target,but shows little to no sensitivity for the 2-sided clamped target.Recall that except for the sixth layer(rear face),there were incidents of ply failure in these 4-sided targets.However,it is expected that for non-penetrating impacts of these 4-sided clamped targets with no incidents of ply failure(e.g.,at a lowerVi),there would be little to no sensitivity to precise projectile impact location.With the exception of Config 4,Fig.17(a)and(b)show that for the non-penetrating impacts at aVi of 200 m/s,the 4-sided clamped targets arrested the projectile faster and with lower peak fabric dynamic deflection than the 2-sided clamped targets,and therefore improved impact performance.However,for the penetrating impacts at aVi of 300 m/s,Fig.17(c)shows that the 2-sided clamped targets consistently resulted in lower residual velocities and therefore improved impact performance relative to the 4-sided clamped targets.For these penetrating shots(i.e.,Fig.17(c)),the 4-sided clamped Config 1 targets showed almost no sensitivity to precise projectile impact location and layer-to-layer alignment,while the 2-sided clamped Config 1 targets did show some sensitivity.This observation is opposite to the trend observed for the non-penetrating impacts of Config 1 targets(i.e.,Fig.17(a)and(b)).

Fig.13.Contours of vertical displacement for 2-sided clamped targets at a Viof 200 m/s(left)Configuration 1a(right)Configuration 2.

Fig.14.Side view of fabric deformation states for 2-sided clamped targets at a Viof 200 m/s(top)Configuration 1a(bottom)Configuration 2.

3.3.Effects of material functional grading

This section investigates the effects of functionally grading(i.e.,Type A and Type B)the Config 1a and Config 2 targets based on varying yarn stiffness and strength values across the plies,while maintaining the same yarn strain energy density.All three inter yarn friction levels(μy-yof 0.10,0.18,0.30)are considered for the baseline Config 1a and Config 2 targets.Here,baseline refers to all plies having the same material properties.However,the functionally graded Config 1a and Config 2 targets initially utilize only the baseline inter-yarn friction(i.e.,μy-yof 0.18).Based on the resulting impact performance,an additional case is then considered using the functionally graded target with a different level of inter-yarn friction.The results of this additional case are highlighted in the red dashed-line frames of figs.18 and 19.Fig.18 compares the impact performance metrics for the 4-sided clamped targets,while Fig.19 compares them for the 2-sided clamped targets.As before,two impact velocities are considered-a non-penetrating shot at aVi of 200 m/s,and a penetrating shot at aVi of 300 m/s.From Fig.18(a)and(b),for the non-penetrating shots,the Type A and Type B Config 1a and Config 2 targets at aμy-yof 0.18 perform either similar toor below the corresponding baseline(i.e.,notfunctionally graded)Config 1a and Config 2 targets also at aμy-yof 0.18.However,when combining the Type B Config 2 target with a lowerμy-yof 0.10,there is a marginal increase in the performance metrics,with a slightly shorter time to arrest the projectile and peak dynamic deflection.Nevertheless,this marginally-increased impact performance is still inferior in comparison to the highest nonpenetrating impact performance obtained from all the cases considered in Fig.18(a)and(b)viz.,the baseline Config 2 target with aμy-yof 0.10.Thus for the 4-sided clamped non-penetrating case,the combination of functional grading and low inter-inter friction level marginally increased the impact performance,but was still below the target with no functional grading and a low inter-yarn friction level.

Fig.15.Impact performance of 4-sided clamped targets(a)time taken to arrest the projectile at a Vi of 200 m/s(b)peak fabric dynamic deflection at a Vi of 200 m/s(c)residual projectile velocity at a Vi of 300 m/s.

Fig.16.Impact performance of 2-sided clamped targets(a)time taken to arrest the projectile at a Vi of 200 m/s(b)peak fabric dynamic deflection at a Vi of 200 m/s(c)residual projectile velocity at a Vi of 300m/s.

Fig.17.Comparison of impact performance of 4-and 2-sided clamped fabric targets(a)time taken to arrest the projectile at a Vi of 200 m/s(b)peak fabric dynamic deflection at a Vi of 200 m/s(c)residual projectile velocity at a Vi of 300 m/s.

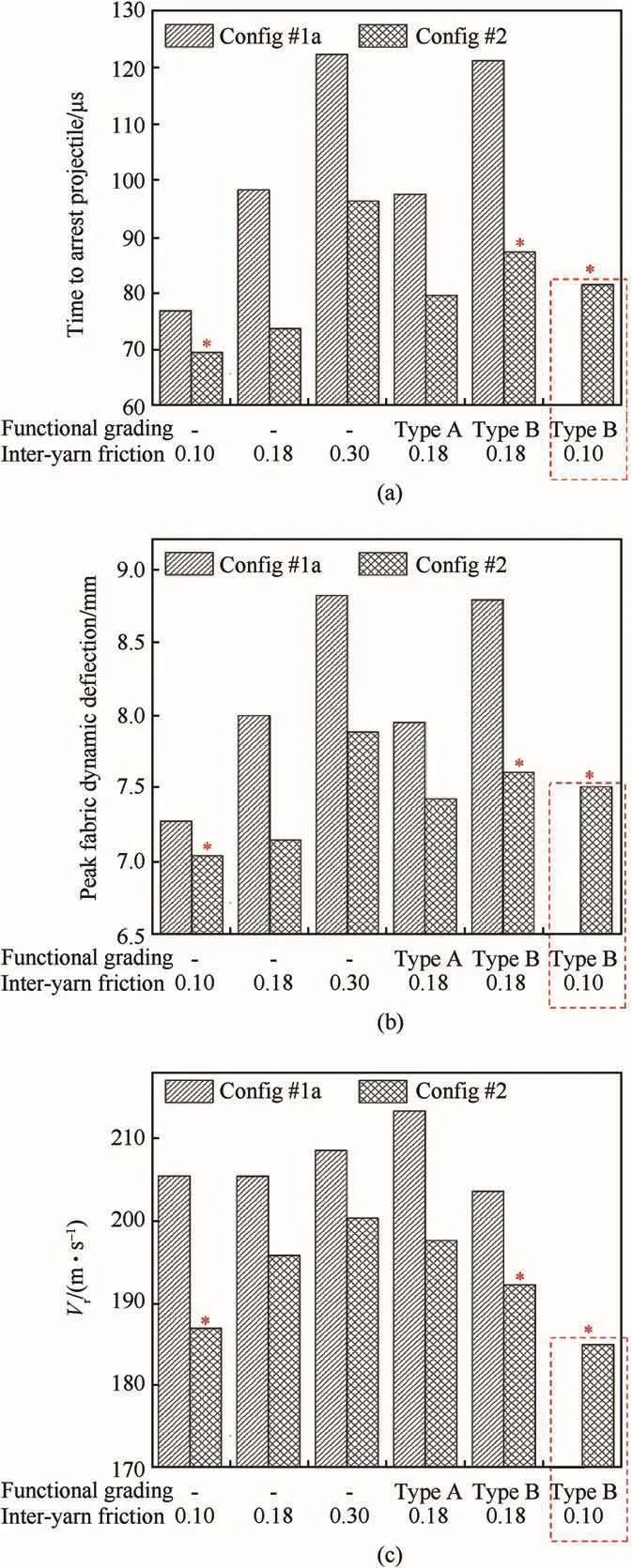
Fig.18.Impact performance of 4-sided clamped functionally graded Configuration 1a and Configuration 2 fabric targets(a)time taken to arrest the projectile at a Vi of 200 m/s(b)peak fabric dynamic deflection at a Vi of 200m/s(c)residual projectile velocity at a Vi of 300 m/s.

From Fig.18(c),for the penetrating shots,while the Type A Config 1a and Config 2 targets at aμy-yof 0.18 perform below the corresponding baseline(i.e.,not functionally graded)Config 1a and Config 2 targets also at aμy-yof 0.18,the Type B Config 1a and Config 2 targets perform better with slightly lower residual velocities.However,when combining the Type B Config 2 target with a lowerμy-yof 0.10,there is a further enhancement of the response,with a noticeably lower residual velocity than the baseline Config 2 target.Furthermore,this residual velocity is also marginally lower than the lowest residual velocity obtained from all the cases considered in Fig.18(c)viz.,the baseline Config 2 target with aμy-yof 0.10.Thus,for the 4-sided clamped penetrating case,the combination of functional grading and low inter-yarn friction level overall enhanced the impact performance.

For the non-penetrating case with the 2-sided clamped targets in Fig.19(a)and(b),functionally grading the targets for both Config 1a and Config 2 had negligible effect on the impact performance metrics in terms of either the time required to arrest the projectile or the peak fabric dynamic deflection.When combining the Type B Config 1a target with a lower inter-yarn friction level,there was no change in impact performance,as shown in Fig.19(a)and(b).In contrast,while the Type A Config 1a and Config 2 targets at aμy-yof 0.18 resulted in higher residual velocities than the corresponding baseline(i.e.,not functionally graded)Config 1a and Config 2 targets also at aμy-yof 0.18,the Type B Config 1a and Config 2 targets resulted in enhanced impact performance,as evidenced by the lower residual velocities in Fig.19(c).When combining the Type B Config 1a target with a lowerμy-yof 0.10,there is a further enhancement in the response,with a noticeably lower residual velocity.Furthermore,this residual velocity is also the lowest of all the residual velocities in Fig.19(c)for the Config 1a targets.Thus,for the 2-sided clamped penetrating impact case,the combination of functional grading and low inter-inter friction level marginally enhanced the impact performance.

A general trend that emerges from Figs.18 and 19 is that there is marginal to noticeable increase in impact performance when using a low inter-yarn friction coefficient and functionally grading the fabric plies with decreasing stiffness away from the strike face,but keeping in mind that the functional grading was performed for a constant yarn strain energy density.Because of the short time scales of the impact event and the much smaller fabric target sizes considered in this study compared to a realistic fabric ballistic pack(for e.g.,28 layers of in-plane dimensions 381 mm×381mm),the reported increases or decreases in impact performance appear small in magnitude(e.g.,magnitudes of peak fabric dynamic deflection and residual velocity),although because this study is deterministic,the trends are valid.However,if statistical variability were considered along with a probabilistic penetration performance,then only those trends that lay outside of the overlapping error bars when comparing performance metrics would be valid,as only they would be statistically meaningful.

Fig.19.Impact performance of 2-sided clamped functionally graded Configuration 1a and Configuration 2 fabric targets(a)time taken to arrest the projectile at a Vi of 200 m/s(b)peak fabric dynamic deflection at a Vi of 200 m/s(c)residual projectile velocity at a Vi of 300m/s.

3.4.Comparison between single layer and multilayer fabric targets

It was shown in Nilakantan and Gillespie[26]that theV50velocities of single-layer plain weave Kevlar fabrics decreased with increasing levels of inter-yarn friction for 4-sided clamped targets,although an increase inV50velocities was observed for 2-sided clamped targets.Furthermore,Nilakantan and Nutt[36]showed that a single-layer Kevlar fabric clamped on 2-sides had a lowerV50velocity than the same target clamped on 4-sides.For the singlelayer 4-sided clamped fabric targets,frictional energy dissipations were negligible in comparison with the magnitudes of fabric internal and kinetic energies.Thus,the role of yarn friction was indirect or secondary in nature,by affecting inter-yarn load sharing and yarn stress patterns at the impact site,and consequently the tensile failure of the principal yarns.For the single-layer 2-sided clamped fabric targets,frictional energy dissipations remained negligible until the central unclamped yarn(s)began to pull out of the fabric weave.Frictional sliding and pullout of a single principal yarn alonewas sufficient to arrest the projectile completely,and the corresponding frictional energy dissipation greatly exceeded the fabric internal and kinetic energies.Single-layer,4-sided clamped fabric targets result in greater initial projectile decelerations than 2-sided clamped targets before the onset of yarn failure,because both the warp and fill yarns are clamped and develop yarn tensions at a faster rate.For single-layer impact,the fabric kinetic energy due to momentum transfer between the projectile and fabric initially grows at a faster rate than the fabric internal energy due to tensile straining of the yarns.However,this kinetic energy reaches smaller peak magnitudes.

There are key differences between the aforementioned single layer fabric impact behavior and that of multi-layer fabric targets.For multi-layer targets,the fabric kinetic energy also initially grows at a faster rate than the fabric internal energy,although it can reach higher peak magnitudes.This can be attributed to the fact that impact event tends to be more ‘localized’around the impact site,and energy dissipations via yarn tensile straining are not spread as far and wide towards the clamped boundaries compared to that observed for single-layer targets.Multi-layer fabric targets also show less sensitivity of the initial rate of projectile deceleration to the clamping configuration.Both 4-sided and 2-sided clamped targets show similar initial projectile decelerations,which are momentum-dominated,but eventually grow apart with 4-sided clamped targets showing faster deceleration rates prior to the onset of yarn failure.

Perhaps the biggest difference between the impact behavior of single-layer and multi-layer fabric targets arises in the frictional mechanisms for 2-sided clamped targets.In multi-layer,2-sided clamped targets,with the possible exception of the last fabric layer(i.e.,away from the strike face),there is no significant yarn pullout or yarn ejection from the fabric weave.Frictional energy dissipations instead arise from small extents of yarn sliding at the cross-over locations and yarn reorientation(or scissoring).This is because inter-layer contact increases frictional forces and restricts the mobility of the yarns in the neighboring layers.The successive intact layer that is directly beneath the preceding failed or penetrated layer prevents the unclamped yarns in the preceding failed layer from pulling out of the weave.However,because the last layer has no ‘backing’,yarns in the last layer(rear face)can get pulled out from the fabric weave in a manner similar to that observed in 2-sided clamped single-layer targets.

While this study did not computeV50velocities for the multilayer fabric targets,the penetrating impact tests showed lower residual projectile velocities for the 2-sided clamped targets,which according to the performance metric considered herein,is considered as improved impact performance over the 4-sided clamped multi-layered fabric targets.Regardless of whether the multi-layer fabric target is 4-sided or 2-sided clamped,yarn friction has both a direct or primary effect,as well as an indirect or secondary effect.The primary effect refers to the magnitudes of frictional energy dissipations,which unlike the single-layer fabric targets,are comparable to those of the fabric internal and kinetic energies.Another difference is that the frictional energy dissipation for multi-layer fabric targets steadily increases during the impact event from the time instant of projectile impact,unlike the single-layer 2-sided clamped target,where a substantial increase in frictional energy dissipation was only observed after the unclamped principal yarn(s)began to pull out of the fabric weave.Projectile-yarn and projectile-fabric frictional interactions are also expected to be significantly more important for multi-layer fabric targets,as the projectile sequentially penetrates and windows through the failed plies.

4.Conclusions

Perhaps the most important finding of this study is that there are significant differences between the underlying impact behaviors of single-layer and multi-layer fabric targets for similar impact scenarios,and that trends observed in single-layer fabric impact studies do not necessarily translate to multi-layer fabric targets.These differences arise not just in the mechanisms of failure and energy dissipation,but also in the sensitivity to material parameters such as inter-yarn friction,and to practical considerations,such as the clamping configuration used during impact testing.This finding is significant,because the literature is replete with numerical studies of single-layer fabric targets at the yarn-level that primarily focus around the effects of yarn friction.However,there is little work in the literature to simulate multi-layer fabric targets,and consequently,the underlying mechanisms that govern their ballistic impact behavior are not as well understood.Addressing this gap in future studies could yield potentially valuable insights.

The use of a stronger and stiffer ballistic fiber would undoubtedly lead to improved fabric ballistic impact behavior,although creating such a new fiber material from the ground up is a challenging endeavor.The choice of ballistic fibers that can be incorporated into soft armor is therefore limited to what is readily available.However,this study has demonstrated that performance improvements in ballistic impact behavior can be realized without changing the underlying fiber material,and instead by tailoring the target architecture in terms of ply orientations and layup patterns,as well as bytailoring the inter-yarn friction.Such tailoring of target architecture is straightforward and can be readily accomplished.However,even advanced tailoring,such as changing the angle between the orthogonal warp and fill yarns in a 2D fabric(i.e.,nonorthogonal or sheared fabric),which in the past was difficult to weave,can nowadays be accomplished with modern braiding machines.Inter-yarn frictional interactions,which are strongly coupled with the fabric weave architecture,can be strategically tailored through the application of coatings and yarn sizing.The ply-level material functional grading technique chosen as a starting point in this study led to slight improvements in impact performance in limited cases,but degraded performance in other cases.Tailoring of yarn stiffness and strength does not necessarily require a new ballistic fiber,but by changing the yarn denier(e.g., fiber bundle size)as well as the weave tightness,the stiffness and strength of individual yarns as well as the mechanical behavior of the overall ply can be respectively tailored.Another option worth considering is the use of hybrid yarns comprised of one or more fiber types,or hybrid fabrics comprised of different yarn materials in the warp and fill directions within the same ply.

The material and architectural parameters studied here only represent a small portion of the parameter space that is available for strategic tailoring and optimization,and further improvements in ballistic impact performance are therefore yet to be realized.This study has demonstrated a path forward for such improvements and design optimizations,driven by numerical simulations,as part of an overall“materials-by-design”paradigm to design improved lightweight body armor.

Declaration of conflicting interests

The author(s)declared no potential conflicts of interest with respect to the research,authorship,and/or publication of this article.

Funding

The authors acknowledge support from the M.C.Gill Composites Center at the University of Southern California(USC).Computation for the work described in this paper was supported by the USC Center for High-Performance Computing(hpcc.usc.edu).

[1]Cheeseman BA,Bogetti TA.Ballistic impact into fabric and compliant composite laminates.Compos Struct 2003;61:161-73.

[2]Tabiei A,Nilakantan G.Ballistic impact of dry woven fabric composites:a review.Appl Mech Rev 2008;61(1):010801-13.

[3]Sockalingam S,Chowdhury SC,Gillespie JW,Keefe M.Recent advances in modeling and experiments of Kevlar ballistic fibrils, fibers,yarns and flexible woven textile fabrics-a review.Text Res J 2017;87(8):984-1010.2017/04:0040517516646039.

[4]David NV,Gao XL,Zheng JQ.Ballistic resistant body armor:contemporary and prospective materials and related protection mechanisms.Appl Mech Rev 2009;62:1-20.

[5]Cavallaro P.Soft body armor:an overview of materials,manufacturing,testing,and ballistic impact dynamics.2011.NUWC-NPT Technical Report 12,057.

[6]Barauskas R,Abraitiene A.Computational analysis of impact of a bullet against the multilayer fabrics in LS-DYNA.Int J Impact Eng 2007;34:1286-305.

[7]Barauskas R,Abraitiene A.Multi-resolution finite element models for simulation of the ballistic impact on non-crimped composite fabric packages.Compos Struct 2013;10(104):215-29.

[8]Nilakantan G,Keefe M,Bogetti TA,Adkinson A,Gillespie Jr JW.On the finite element analysis of woven fabric impact using multiscale modeling techniques.Int J Solid Struct 2010;47(17):2300-15.

[9]Nilakantan G,Keefe M,Bogetti TA,Gillespie Jr JW.Multiscale modeling of the impact of textile fabrics based on hybrid element analysis.Int J Impact Eng 2010;37(10):1056-71.

[10]Jia X,Huang Z,Zu X,Gu X,Xiao Q.Effect of mesoscale and multiscale modeling on the performance of kevlar woven fabric subjected to ballistic impact:a numerical study 2013;20(6):1195-214.

[11]Ha-Minh C,Kanit T,Boussu F,Imad A.Numerical multi-scale modeling for textile woven fabric against ballistic impact.Comput Mater Sci 2011;50:2172-84.

[12]Ha-Minh C,Boussu F,Imad A,Kanit T,Crepin D.Multi-scale model to predict the ballistic impact behavior of multi-layer plain-woven fabrics.Int J Comput Meth 2014 06/01;11(03),1343011.2017/07.

[13]Wang Y,Miao Y,Swenson D,Cheeseman BA,Yen C,LaMattina B.Digital element approach for simulating impact and penetration of textiles.IntJImpact Eng 2010 5;37(5):552-60.

[14]Nilakantan G.Filament-level modeling of Kevlar KM2 yarns for ballistic impact studies.Compos Struct 2013;104:1-13.

[15]Rao MP,Nilakantan G,Keefe M,Powers BM,Bogetti TA.Global/local modeling of ballistic impact onto woven fabrics.J Compos Mater 2009;43(5):445-67.

[16]Sockalingam S,Gillespie JW,Keefe M.Modeling the fiber length-scale response of Kevlar KM2 yarn during transverse impact.Text Res J 2017;87(18):2242-54.2017/08:0040517516669074.

[17]Recchia S,Zheng JQ,Horner S,Pelegri AA.Multiscale modeling of randomly interwoven fibers for prediction of KM2 Kevlar yarn strength and damage.Acta Mech 2015 12/01;226(12):4149-58.

[18]del Sorbo P,Girardot J,Dau F,Iordanoff I.Numerical investigations on a yarn structure at the microscale towards scale transition.Compos Struct 2018;183:489-98.

[19]Wang Y,Miao Y,Huang L,Swenson D,Yen C,Yu J,et al.Effect of the inter- fiber friction on fiber damage propagation and ballistic limit of 2-D woven fabrics under a fully confined boundary condition.Int J Impact Eng 2016;11(97):66-78.

[20]Grujicic M,Hariharan A,Pandurangan B,Yen CF,Cheeseman BA,Wang Y,et al.Fiber-level modeling of dynamic strength of Kevlar KM2 ballistic fabric.J Mater Eng Perform 2011.https://doi.org/10.1007/s11665-011-0006-1.

[21]Grujicic M,Ramaswami S,Snipes JS,Galgalikar R.Finite-element-based fiberlength-scale modeling of the ballistic-impact response of Kevlar KM2 fabric.Textil Light Ind Sci Technol 2016;5:1-15.

[22]Nilakantan G,Nutt S.State of the art in the deterministic and probabilistic ballistic impact modeling of soft body armor: filaments to fabrics.In:American society for Composites 29th technical conference;September 8-10,2014.San Diego,CA,USA.

[23]Nilakantan G,Keefe M,Wetzel ED,Bogetti TA,Gillespie Jr JW.Computational modeling of the probabilistic impact response of flexible fabrics.Compos Struct 2011;93:3163-74.

[24]Nilakantan G,Keefe M,Wetzel ED,Bogetti TA,Gillespie Jr JW.Effect of statistical yarn tensile strength on the probabilistic impact response of woven fabrics.Compos Sci Technol 2012;72(2):320-9.

[25]Nilakantan G,Wetzel ED,Bogetti TA,Gillespie Jr JW.Finite element analysis of projectile size and shape effects on the probabilistic penetration response of high strength fabrics.Compos Struct 2012;94(5):1846-54.

[26]Nilakantan G,Gillespie Jr JW.Ballistic impact modeling of woven fabrics considering yarn strength,friction,projectile impact location,and fabric boundary condition effects.Compos Struct 2012;94(12):3624-34.

[27]Duan Y,Keefe M,Bogetti TA,Cheeseman BA,Powers B.A numerical investigation of the influence of friction on the energy absorption by a high-strength fabric subjected to ballistic impact.Int J Impact Eng 2006;32:1299-312.

[28]Jia X,Sun B,Gu B.A numerical simulation on ballistic penetration damage of 3D orthogonal woven fabric at microstructure level.Int J Damage Mech 2012;21(2):237-66.

[29]Chocron S,Figueroa E,King N,Kirchdoerfer T,Nicholls AE,Sagebiel E,et al.Modeling and validation of full fabric targets under ballistic impact.Compos Sci Technol 2010 11/15;70(13):2012-22.

[30]Rao MP,Duan Y,Keefe M,Powers BM,Bogetti TA.Modeling the effects of yarn material properties and friction on the ballistic impact of a plain-weave fabric.Compos Struct 2009;89(4):556-66.

[31]Nilakantan G,Keefe M,Gillespie Jr JW,Bogetti TA,Adkinson R.A study of material and architectural effects on the impact response of 2D and 3D dry textile composites using LS-DYNA.In:7th European LS-DYNA conference;May 14-15,2009.Salzburg,Austria.

[32]Nilakantan G,Keefe M,Gillespie Jr JW,Bogetti T,Adkinson R.A numerical investigation into the effects of 3D architecture on the impact response of flexible fabrics.In:Second world conference on 3D fabrics and their applications;April 6-7,2009.Greenville,South Carolina,USA.

[33]Tran P,Ngo T,Yang EC,Mendis P,Humphries W.Effects of architecture on ballistic resistance of textile fabrics:numerical study.Int J Damage Mech 2014;23(3):359-76.

[34]Erol O,Powers BM,Keefe M.Effects of weave architecture and mesoscale material properties on the macroscale mechanical response of advanced woven fabrics.Compos Appl Sci Manuf 2017;101:554-66.

[35]Ha-Minh C,Boussu F,Kanit T,Cra©pin D,Imad A.Effect of frictions on the ballistic performance of a 3D warp interlock fabric:numerical analysis.Appl Compos Mater 2012 06/01;19(3):333-47.

[36]Nilakantan G,Nutt S.Effects of clamping design on the ballistic impact response of soft body armor.Compos Struct 2014;108:137-50.

[37]Nilakantan G,Nutt S.Effects of fabric target shape and size on the V50 ballistic impact response of soft body armor.Compos Struct 2014;116:661-9.

[38]Zhang GM,Batra RC,Zheng J.Effect of frame size,frame type,and clamping pressure on the ballistic performance of soft body armor.Composites 2008;39:476-89.

[39]Nilakantan G,Wetzel ED,Bogetti TA,Gillespie Jr JW.A deterministic finite element analysis of the effects of projectile characteristics on the impact response of fully clamped flexible woven fabrics.Compos Struct 2013;95:191-201.

[40]Egres RG.Anonymous Fabric architectures for improved ballistic impact performance.November 4,2010.US 2010/0275764 A1.

[41]Nilakantan G,Gillespie JWJ,Keefe M.Anonymous Ballistic resistant fabric armor.June 24,2010.US 2010/0154621 A1.

[42]Ballistic resistance of body armor.National Institute of Justice;2008.NIJ Standard-0101.06.

[43]Yang HH.Kevlar aramid fiber.New York:John Wiley&Sons;1993.p.71-102.

[44]Kim J,McDonough WG,Blair W,Holmes GA.The modified-single fiber test:a methodology for monitoring ballistic performance.J Appl Polym Sci 2008;108:876-86.

[45]Nilakantan G,Abu-Obaid A,Keefe M,Gillespie Jr JW.Experimental evaluation and statistical characterization of the strength and strain energy density distribution of Kevlar KM2 yarns:exploring length-scale and weaving effects.J Compos Mater 2011;45(17):1749-69.

[46]Dong Z,Sun CT.Testing and modeling of yarn pull-out in plain woven Kevlar fabrics.Compos Appl Sci Manuf 2009 12;40(12):1863-9.

[47]Briscoe BJ,Motamedi F.The ballistic impact characteristics of aramid fabrics:the influence of interface friction.Wear 1992;158:229-47.