地震激励下参数不确定结构重叠分散保性能控制

, ,

(合肥工业大学 土木与水利工程学院,合肥 230009)

1 引 言

工程结构振动控制问题近年来在理论和应用上均有着较大的发展,受到国内外相关专家们的重视[1]。在建立工程结构力学模型的过程中,无法精确确定结构的刚度和质量等参数,使得力学模型具有参数不确定性。结构参数的不确定性会引起控制系统的不稳定,导致控制效果不理想。

文献[2-4]分别针对不确定离散系统、不确定离散状态时滞系统以及不确定连续状态时滞系统,设计了重叠分散保性能控制器。Lien等[5]研究了不确定系统无外界干扰输入的鲁棒分析和有外界干扰输入的H∞控制方法；Tlili等[6]针对非线性不确定关联系统,提出了基于观测器反馈的鲁棒保性能分散控制方法；文献[7,8]设计了基于双线性矩阵不等式的保性能控制方法,分别解决了不确定离散状态时滞系统和不确定离散状态输入时滞系统的振动控制问题；Ahmadi等[9]针对一类不确定线性系统,研究了静态输出反馈重叠分散保性能控制方法。

大尺度工程结构系统具有未知量多和计算量大的特性,采用集中控制策略,若中央控制器失效,则整个控制系统失效。重叠分散控制策略将工程结构划分成一组独立的子系统,每一个子系统使用局部信息独立控制,为解决大尺度工程结构振动控制问题开辟了新途径[10-13]。

本文采用重叠分散控制策略,将高层建筑结构划分成一组子结构,对每一个子结构采用保性能控制方法设计控制器,提出了地震荷载作用下参数不确定结构重叠分散保性能控制方法。数值模拟结果验证了本文方法解决大尺度工程结构振动控制问题的有效性、可靠性和稳定性。

2 基本理论

考虑结构参数的不确定性,n层剪切型建筑结构(图1)的力学模型为

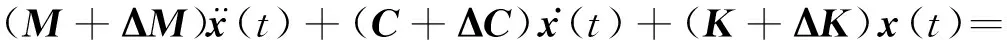
(1)

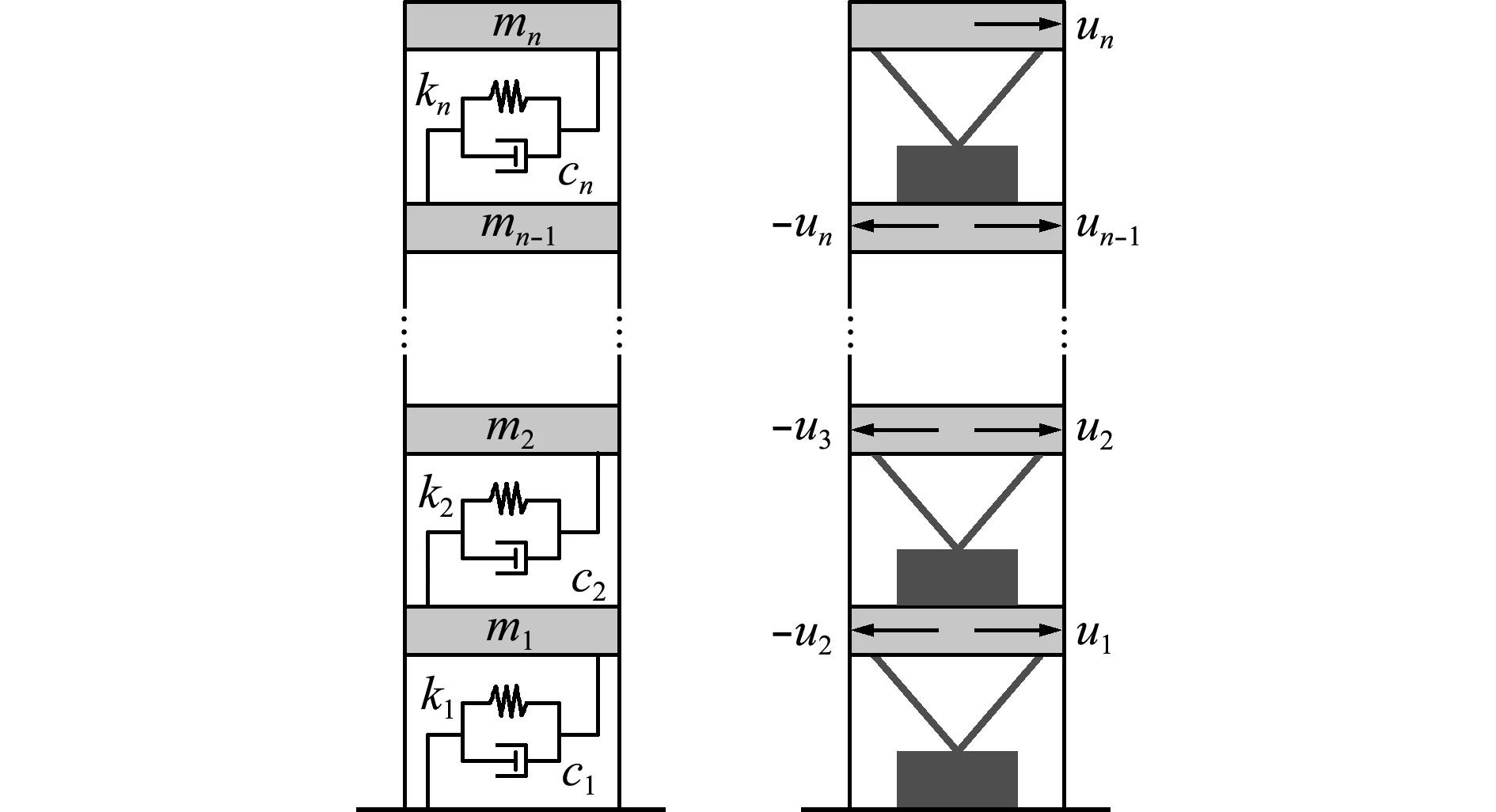
图1n层剪切型建筑结构模型

Fig.1 Mechanical model of then-story shear-type building

C=a0M+a1K

(2)

Ds=-(M+ΔM)[1]n ×1

(3)

ΔM=αδMM,ΔC=βδCC,ΔK=γδKK

(4)

式中α,β和γ为最大变化率，δM,δC和δK为未知实函数矩阵。由于δM是对角矩阵,则有[14,15]

(M+ΔM)-1=M-1+Δ1M

Δ1M=-(αM-1)δM(I+αδM)-1

(5)

方程(1)的状态空间形式如下：

(6)

式中

ΔM K=Δ1M(K+ΔK)+M-1ΔK

ΔM C=Δ1M(C+ΔC)+M-1ΔC

(ΔApΔBp)=DpFp(Ep 1Ep 2)

(7)

(8)

(9)

则新的状态空间方程可表示为

(10)

(11)

考虑一对参数不确定的线性系统：

y(t)=CyZ(t)

(12)

(13)

式中M,N和L为补偿矩阵[2,10]。

链型结构形式的剪切型建筑结构可表示成具有L个链型子系统互联,如图2所示,子系统1与子系统2组成一个子系统对,子系统2与子系统3组成一个子系统对,子系统3与子系统4组成一个子系统对,以此类推子系统N-1与子系统N组成一个子系统对。

移去相互耦联的分块矩阵[10-12],大尺度系统分解成L=N-1个相互独立的成对子系统：

(i=1,2,…,L) (14)

式中

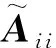
(15)

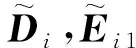
图2L个串联子系统结构

Fig.2 Schematic of the chain structure withN-subsystems

(16)

(17)

(18)

(19)

(20)

s.t. (i) 方程(20)

(21)

3 算例仿真

选取20层Benchmark建筑结构剪切模型,在结构的每层均设置控制装置,如图1所示。结构参数参考文献[11]。

结构刚度最大变异为±15%。选用Hachinohe地震波,峰值调整为3 m/s2,持续时间为35 s,采样步长为0.02 s。

(22)

为了验证本文方法(ODGCC)的优越性,将其与集中保性能控制方法(CGCC)进行分析比较。

图3 重叠分散子系统配置

Fig.3 Overlapping decentralized subsystem configuration

无控状态、集中保性能控制(CGCC)和重叠分散保性能控制(ODGCC)三种方法获得的结构层间位移峰值计算结果列入表1。可以看出，(1) 当结构刚度摄动为0时,CGCC方法的层间位移峰值控制效果达到44.30%～92.56%,ODGCC方法的层间位移峰值控制效果达到41.49%～77.94%；(2) 当结构刚度摄动为+15%时,CGCC方法层间位移峰值控制效果达到33.62%～91.55%,ODGCC方法的层间位移峰值控制效果达到35.25%～74.73%；(3) 当结构刚度摄动为-15%时,CGCC方法的层间位移控制效果达到49.24%～94.58%,ODGCC方法层间位移峰值控制效果达到54.16%～81.64%。

表1 层间位移峰值比较Tab.1 Comparison of inter-story displacement peak

图4 层间位移峰值(ΔK=0)

Fig.4 Maximal inter -story drifts (ΔK=0)

图5 层间位移峰值(ΔK=+0.15K)

Fig.5 Maximal inter -story drifts (ΔK=+0.15K)

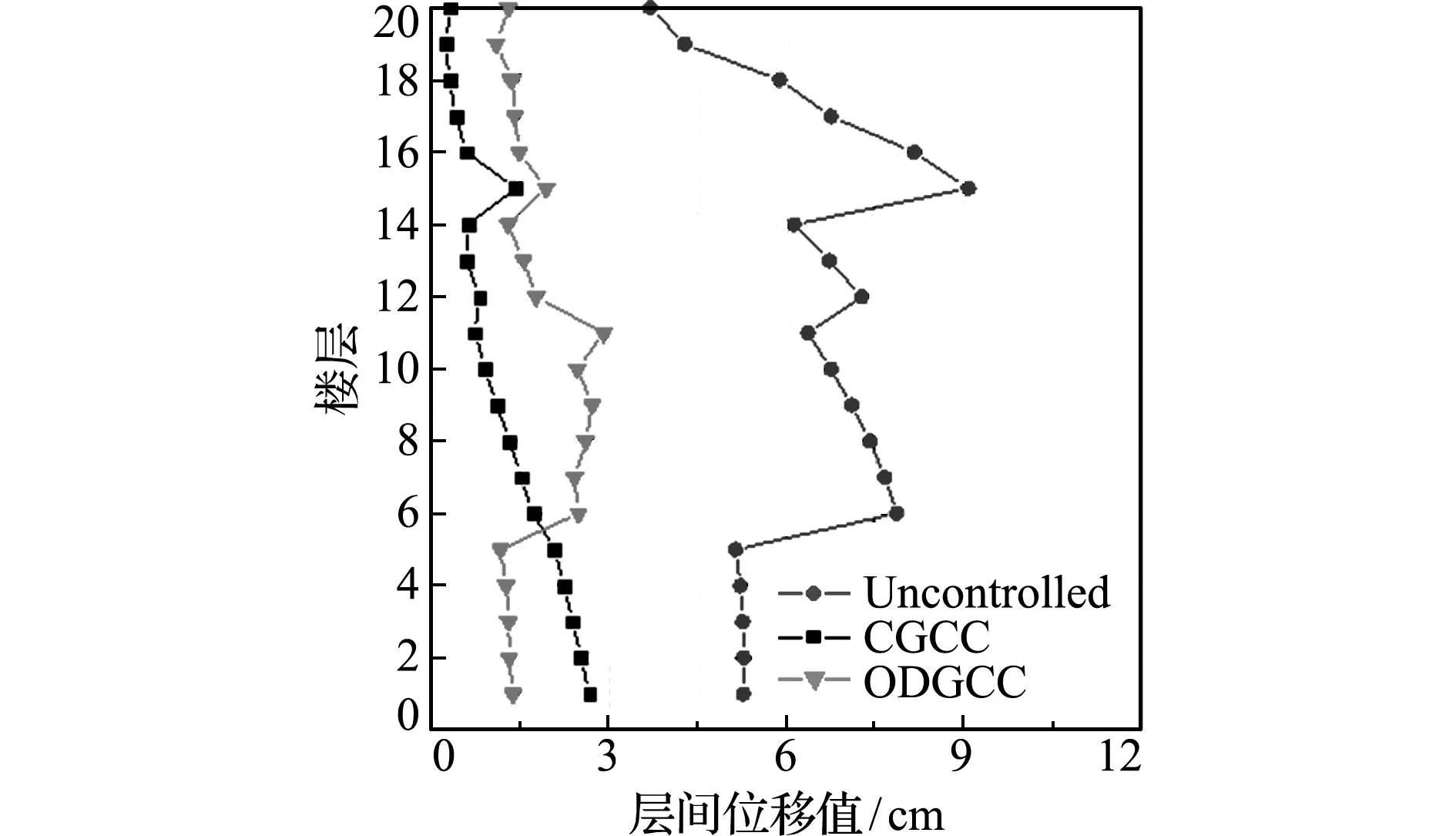
图6 层间位移峰值(ΔK=-0.15K)

Fig.6 Maximal inter -story drifts (ΔK=-0.15K)

图7 顶层加速度曲线(ΔK=0)

Fig.7 Acceleration curves of the top floor (ΔK=0)

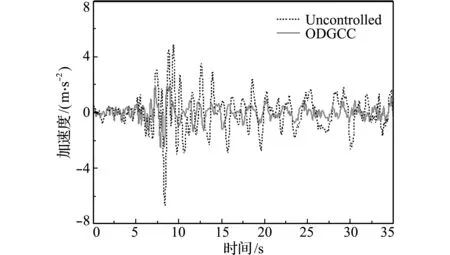
图8 顶层加速度曲线(ΔK=+0.15K)

Fig.8 Acceleration curves of the top floor (ΔK=+0.15K)

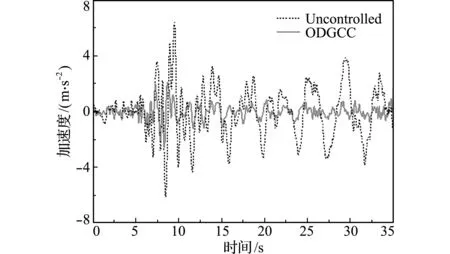
图9 顶层加速度曲线(ΔK=-0.15K)

Fig.9 Acceleration curves of the top floor (ΔK=-0.15K)

图4～图9分别给出了刚度摄动为0,+15%和-15%时结构的层间峰值位移以及顶层加速度时程曲线。可以看出,对于刚度不确定性结构,本文提出的方法对层间位移峰值的控制取得了很好的效果,同时很好地抑制了结构顶层加速度响应。

4 结 语

本文提出了不确定建筑结构在地震荷载作用下振动控制的重叠分散保性能控制方法。考虑其刚度不确定性,采用集中保性能控制和重叠分散保性能控制方法，分别对20层Benchmark模型进行了数值模拟。结果表明,对于参数不确定结构,本文方法能够有效地降低结构的地震响应，并能很好地抑制层间位移峰值和结构加速度响应。

实际工程中,结构的参数不确定性广泛存在,研究不确定结构的振动控制问题具有重要意义。本文方法适用于大尺度结构的振动控制问题。

:

[1] Thenozhi S,Yu W.Advances in modeling and vibration control of building structures[J].AnnualReviewsinControl,2013,37(2):346-364.

[2] Bakule L,Rodellar J,Rossell J M.Overlapping guaranteed cost control for time -varying discrete -time uncertain systems [J].ProceedingsoftheAme-ricanControlConference,2002,2:1705-1710.

[3] Bakule L,Rodellar J,Rossell J M.Robust overlapping guaranteed cost control of uncertain state -delay discrete -time systems[J].IEEETransactionsonAutomaticControl,2006,51(12):1943-1950.

[4] Rossell J M,Palacios-Quinonero F.Design of guaranteed cost overlapping controllers for a class of uncertain state -delay systems[A].American Control Conference[C].St.Louis,MO,USA,2009.

[5] Lien C H,Yu K W.LMI optimization approach on robustness andH∞control analysis for observer-based control of uncertain systems[J].Chaos,Solitons&Fractals,2008,36(3):617-627.

[6] Tlili A S,Dhbaibi S,Braiek N B.Robust decentralised observer based guaranteed cost control for nonlinear uncertain interconnected systems.Application to multi-machine power systems[J].InternationalJournalofSystemsScience,2012,43(9):1713-1727.

[7] Nian X,Sun Z,Wang H,et al.Bilinear matrix inequa-lity approaches to robust guaranteed cost control for uncertain discrete -time delay system[J].OptimalControlApplicationsandMethods,2013,34(4):433-441.

[8] Zhou X,Dong T,Tang X,et al.A BMI approach to guaranteed cost control of discrete -time uncertain system with both state and input delays[J].OptimalControlApplicationsandMethods,2015,36(6):844-852.

[9] Ahmadi A,Aldeen M,Abdolmaleki M.Robust overlapping output feedback control design in uncertain systems with unknown uncertainty bounds[A].Control Conference (AUCC),5t hAustralian[C].Gold Coast,QLD,Australia,2015.

[10] Palacios-Quionero F,Rossell J M,Karimi H R.Semi-decentralized strategies in structural vibration control[J].Modeling,IdentificationandControl,2011,32(2):57-77.

[11] 汪 权,庄嘉雷,张 俊,等.地震作用下高层建筑结构的重叠分散控制研究[J].计算力学学报,2015,32(1):48-52,58.(WANG Quan,ZHUANG Jia-lei,ZHANG Jun,et al.Overlapping decentralized control of tall buildings under earthquakes[J].ChineseJournalofComputationalMechanics,2015,32(1):48-52,58.(in Chinese))

[12] 康小方,王建国,许庆虎.建筑结构振动系统的多重叠分散静态输出反馈H∞控制方法[J].计算力学学报,2015,32(1):53-58.(KANG Xiao -fang,WANG Jian-guo,XU Qing-hu.Multi-overlapping decentralized static output-feedbackH∞control approach on vibration systems of tall building[J].ChineseJournalofComputationalMechanics,2015,32(1):53-58.(in Chinese))

[13] Chen X B,Xu W B,Huang T Y,et al.Pair-wise decomposition and coordinated control of complex systems[J].InformationSciences,2012,185(1):78-99.

[14] Kim S J,Choi J W.Parametric uncertainty in controlling the vibration of a building[A].39t hSICE Annual Conference[C].Iizuka,Japan,2000.

[15] Fill J A,Fishkind D E.The moore -penrose genera-lized inverse for sums of matrices[J].SIAMJournalonMatrixAnalysisandApplications,2000,21(2):629-635.

[16] 俞 立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.(YU Li.RobustControl,LinearMatrixInequalityApproach[M].Beijing:Tsinghua University Press,2002.(in Chinese))