培养逻辑思维是提升数学素养的直通车

杨 宏

（甘肃省兰州市城关区宁兴小学，甘肃 兰州）

一、逻辑思维

逻辑思维又称为抽象思维，是思维的一种高级表现形式。其特点是以抽象的概念、严谨的判断和合理的推理为思维的基本形式，以分解、综合、比较、运用、抽象和具体作为思维的基本过程，从而揭露事物的本质特点和一般规律。

小学阶段，是儿童思维发展的一个重大转折期。学生进入小学就要开始系统地学习人类目前已经掌握的自然知识和社会常识。在学习的过程中，儿童心理过程的有意性和抽象概括性也随之获得发展。

二、小学儿童思维发展的特征

（一）小学儿童的思维仍表现出很大的具体性

低年级儿童所掌握的概念大都是具体的、可以直接感知的。中高年级的学生才逐步学会分出概念中本质的东西和非本质的东西，他们的思维活动仍然具有很大的具体形象性。

如：“什么是三角形？”低年级学生回答：“粽子是三角形。”中高年级学生回答：“是由三条首尾连接的线段组成的闭合图形。”

（二）小学儿童的思维存在着不均衡性

在整个小学阶段儿童思维中的具体形象成分和抽象成分的关系在不断发生变化，但这个变化存在不均衡性。

同一年龄的学生思维发展是不一样的，学习了有关路程的数量关系，少部分学生能够举一反三，大部分只能接受消化一种数量关系。

三、培养儿童思维发展的方法

培养学生的逻辑思考能力，促进学生逻辑思维的发展，是小学数学教育的核心之一。

（一）借用语言表述，有助于调节自己的思维活动，使之逐渐完善

首先说读题，就是要求学生先读题再审题。读题时学生初步完成对文字的阅读，审题时就要抓住关键信息进行解读。训练时可以去掉情景性描述，只留下一些具体的数学信息，还可以将题目中的问题和已知条件互换，使其更加符合学生的思维方式。

如：大米和面粉各买18袋，共需多少钱？

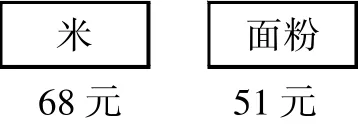
可以复述成大米每袋68元，买18袋，面粉每袋51元，买18袋，大米和面粉共需多少钱？

其次说思路，就是训练学生用完整的语言清晰准确地把自己的解题思路说出来，使学生的思维方法得到巩固。

如：甲乙两地相距440千米，一辆汽车从甲地开往乙地，已经行了140千米，剩下的路程每小时行60千米，还要行几小时？可以从已知条件入手，两地相距440千米，已经行了140千米，剩下的路程是300千米，每小时行60千米，可以得出几小时行完。

再次说算式，就是训练学生说出列式理由，可以讲解算式中每个数字具体表示的含义是什么，还可以说每个算式所隐含的计算道理，如：学生列式 440-140=300（千米），300÷60=5（小时）要求学生说出每个算式表示什么。

说算式的过程能反映学生理解问题和解决问题的能力，能反映学生是否明白问题中的算理。诸如此类的解题，能促进学生对题意的理解，提升学生的逻辑思维能力。

（二）借助信息技术手段，改变学生思维方式

儿童思维的基本特征是以具体形象思维为主，逐步过渡到以逻辑思维为主。在这种情况下，多媒体可以帮助学生初步理解知识，完成思维的转变。

在相遇问题的解决过程中，首先让学生复习行程问题数量关系（路程=时间×速度，时间=路程÷速度，速度=路程÷时间）为知识迁移做好准备。如：王叔叔从王庄拉了一车化肥去县城卖，汽车每小时行40千米，3小时后到达县城，返回王庄时用了2小时，王叔叔返回时的速度是多少？

先利用多媒体制成课件，演示情景，帮助学生理解来回的路程是一样的。最后学生经过思考，提出如下解法：

经过学生的讨论和比较，理清了算理。这样使学生逐步从感性认知跨越到理性认知，又从理性认知回归感性认知，经过这样多层次、多阶段的思维过程，加深了学生对新知识的理解。

（三）借助示意图，使思维更明了

通过画示意图将要解决的问题和已知条件形象地表示出来，使学生直观地获取感性材料和丰富的表象，使学生由感性认识上升到理性认识阶段，从而使其分析、比较能力得到提高。

如：有一堆煤，第一天运走了总数的，第二天运走了余下的，这时剩下120吨，求这堆煤的总吨数？

学生可以理解为，第一天运了，余了，第二天运了余下的，也就是这时剩下剩下的占全部的，也就是120吨，则全部的为（吨）。也可以理解为，第一天运了，余，第二天运了余下的，现在剩下余下的，也就是剩下的有120吨，则全部的有

在解决问题的教学中，培养学生的思维能力是小学数学研究工作中的一项重要课题。只要我们注意寻找适当的教学方法，通过一定形式的训练，就可以使学生具备一定的逻辑思维能力，提升学生的数学素养。