履带式移动机器人轨迹跟踪控制技术研究
, ,,
(同济大学 机械与能源工程学院,上海 201804)
移动机器人是一种能够通过自身状态和传感器信息,在没有人为干预且无需对环境进行任何规定和改变的条件下,实现面向目标的自主运动并完成相应任务的机器人综合系统.该系统集人工智能、信息处理、智能控制、图像处理等专业技术于一体,跨越机械工程、计算机工程、电子工程等多个学科,是目前科学技术发展最活跃的领域之一[1].近年来,随着机器人技术的飞速发展,移动机器人已在工业、农业、军事等领域中得到广泛应用[2].
根据移动方式的差异,移动机器人可以分为轮式移动机器人、蠕动式移动机器人、腿式移动机器人、履带式移动机器人等类型[3].其中轮式移动机器人操作简单,机械性能稳定,但在复杂路面上的运行能力较差,不具有越野性能,应用环境单一;蠕动式移动机器人虽然在特殊环境有其独特的优越性,但是承载能力和运动平稳性较差;腿式移动机器人由于其结构自由度太多,控制比较复杂,运行速度较慢,应用受到一定程度的限制;而履带式移动机器人因为对地压力小,不容易出现打滑现象,牵引性能良好,能够很好地适应特殊地形,所以对其开展的研究得以蓬勃发展.
运动控制是移动机器人自主性研究中最基本的问题,因为移动机器人要自主完成的任何一项任务都是以运动为基础的.根据控制目标的不同,运动控制问题可被分为位姿镇定、轨迹跟踪以及路径跟随3种基本问题[4].其中位姿镇定是指从指定的初始位置出发,稳定达到给定的终点位置;轨迹跟踪与路径跟随是指从指定的初始状态出发,到达并跟踪指定的期望曲线.后两者的主要区别在于:轨迹跟踪的期望曲线是依赖于时间的函数,而路径跟随的期望曲线是不包含时间参数的变量,可以看作是轨迹跟踪的一种特殊情况;同时,轨迹跟踪还要求速度以及加速度与时间相关联,显然难度更大,研究价值更高,现已成为移动机器人运动控制研究领域中的热点问题[5].
针对轨迹跟踪问题,国内外学者已经提出一些控制方法与解决方案.吴剑等[6]应用Back-Stepping控制法实现了轮式移动机器人的轨迹跟踪控制,但该方法的设计过程过于复杂.Park等[7]提出了用于轮式移动机器人的滑模控制法,通过将机器人的速度与角速度控制到滑模面内来实现轨迹跟踪,但其自身不可避免地输入抖振问题,增加了设计难度并降低了控制精度.Fateh等[8]提出了一种基于模糊控制的微调控制器,其性能优于PD模糊控制,可有效保证轨迹跟踪的稳定性,但模糊控制的隶属度函数和控制规则通常依靠专家经验进行建立,存在人为的主观因素,且在控制过程中不能实时修正,直接影响控制结果.此外,神经网络控制技术也逐渐应用于移动机器人的轨迹跟踪问题[9-10].但是,神经网络需要在线或离线学习,占用大量系统资源,轨迹跟踪控制的实时性难以保证.
本文针对履带式移动机器人的自主运动控制技术进行了研究.为了能够实现轨迹跟踪控制,提出了履带式移动机器人的运动学模型和轨迹跟踪动态误差模型.基于Lyapunov函数与轨迹跟踪动态误差模型,提出了一种状态反馈控制算法,并通过稳定性分析证明了该算法能够实现对期望轨迹的跟踪.为了测试所提方法的性能,在给定的初始条件下,进行了Matlab/Simulink环境下的轨迹跟踪仿真实验.通过仿真实验的结果验证了所提方法的有效性和可实现性.
1 履带式移动机器人模型建立
1.1 运动学模型
履带式移动机器人通过两侧履带差动驱动的运动学控制方式,实现各种工况下的作业,其运动轨迹与控制输入、地面性质以及行驶状态都有较大关系.为了便于模型建立,现对履带式移动机器人及其运动做出以下合理假设:① 移动机器人在二维平面内运动;② 整个机器人为刚体,履带与地面完全接触且不产生滑动;③ 两侧履带完全相同,其中心连线与机器人前后运动方向相互垂直.
基于以上假设,履带式移动机器人的运动学模型如图1所示.

图1 履带式移动机器人运动学模型Fig.1 Kinematic model of the tracked mobile robot
图1中:Oxy为全局坐标系;θP为机器人运动正方向与全局坐标系x轴正方向之间的姿态角;P为机器人的质心,在全局坐标系中的坐标是(xP,yP);vP为机器人质心P处的行驶速度;vL为左侧履带的行驶速度;vR为右侧履带的行驶速度;ωP为机器人的转向角速度;C为旋转瞬心;R为转弯半径;L为机器人车体宽度;d为单侧履带宽度.
根据全局坐标系中的几何关系,可以推导出履带式移动机器人的运动学模型为
(1)
由于在机器人进行转向时,各处转向角速度相等,故可以推导出
(2)
联立求解可得
通过式(3)与式(4)可知,机器人质心的行驶速度与转向角速度可根据左、右两侧履带的行驶速度获得.
1.2 轨迹跟踪动态误差模型
履带式移动机器人的轨迹跟踪问题可以描述为在全局坐标系下,机器人从初始位置出发,到达并且跟踪给定的期望轨迹,该期望轨迹由参考机器人的运动轨迹来描述,如图2所示.
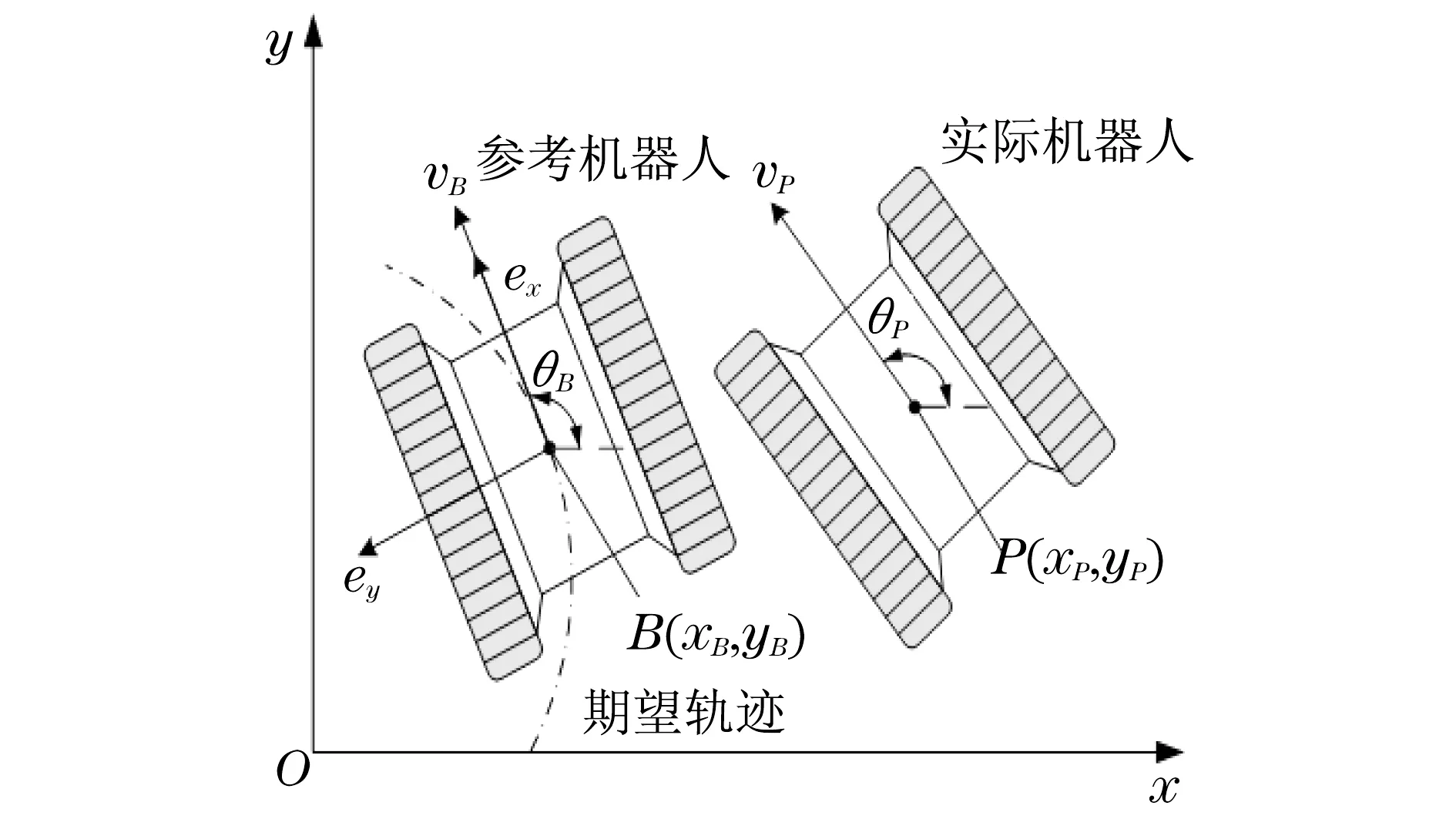
图2 履带式移动机器人轨迹跟踪误差模型Fig.2 Trajectory tracking error model of the tracked mobile robot
图2中:θB为参考机器人的姿态角;B为参考机器人的质心,在全局坐标系中的坐标是(xB,yB);vB为参考机器人质心B处的行驶速度,也称期望速度.
同样,参考机器人的运动学模型可表示为
(5)
式中:ωB为参考机器人的转向角速度,也称期望角速度.
通过将全局坐标系转换为机器人自身坐标系,参考机器人与实际机器人之间的轨迹跟踪误差模型可以表示为
(6)
式中:ex为纵向位移误差;ey为水平位移误差;eθ为姿态角误差.
对式(6)进行微分,可以得到履带式移动机器人的轨迹跟踪动态误差模型为
(7)
因此,本文所研究的轨迹跟踪控制目标就转变为寻找合适的期望控制输入vP和ωP,在控制律的作用下,到达并且跟踪指定的期望轨迹.该目标可以表示为
(8)
2 轨迹跟踪控制
2.1 控制律设计
Lyapunov稳定性理论[11-12]是设计控制律的常用工具.为有效控制履带式移动机器人,针对式(7),首先构造一个正定的Lyapunov函数:
(9)
式中:K1>0且有界.
对式(9)进行微分,可得
(10)
若控制输入选取为
(11)
式中:K2>0,K3>0,且都有界.
将式(11)代入式(10),可得
(12)
2.2 稳定性分析

(13)
3 仿真实验研究
3.1 系统仿真
为了评估本文所提出的控制律性能,在Matlab/Simulink环境下,对履带式移动机器人分别进行直线轨迹跟踪和圆形轨迹跟踪仿真实验.在仿真实验中,假设位移误差、姿态角误差、行驶速度以及转向角速度可以测量或计算得到,控制器动作为实际机器人的行驶速度与转向角速度.仿真模型结构如图3所示.
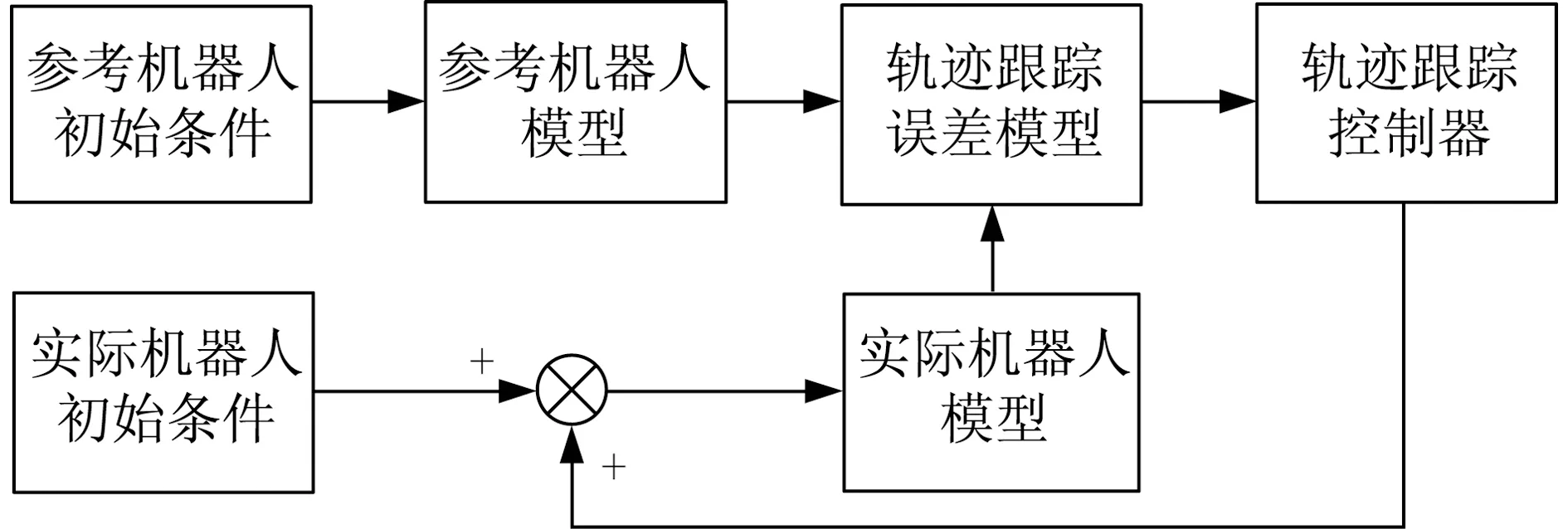
图3 轨迹跟踪控制仿真模型结构框图Fig.3 Structure diagram of the trajectory tracking control simulation model
图3中:初始条件模块为机器人模块提供相对应的初始位置、姿态角、行驶速度与转向角速度;机器人模型模块根据输入的行驶速度与转向角速度进行积分计算,计算出随时间变化的轨迹信息,包括位置与姿态角信息;轨迹跟踪误差模型模块根据参考机器人与实际机器人的轨迹信息计算得到轨迹跟踪误差,并转化到机器人自身坐标系上;轨迹跟踪控制器模块则根据误差信息和控制律进行计算,得到控制输入的行驶速度与转向角速度.
3.2 仿真实验与结果
3.2.1直线轨迹跟踪仿真实验
设置参考机器人的初始位置和姿态角为(2, 0, 0.25π),行驶速度为0.5 m/s,转向角速度为0 rad/s;设置实际机器人的初始位置和姿态角为(1, 1, 0.5π),行驶速度为0 m/s,转向角速度为0 rad/s;轨迹跟踪控制器的参数为K1=0.909,K2=1.250,K3=0.818;仿真时间为20 s.直线轨迹跟踪仿真实验的轨迹曲线、误差曲线和控制输入曲线分别如图4、图5和图6所示.
从图4可以看出,参考机器人的期望轨迹是一条与x轴正方向夹角为45°的倾斜直线,实际机器人在仿真开始时具有一定的轨迹跟踪误差,但是经过轨迹跟踪控制后,实际机器人与参考机器人的轨迹重合.从图5可以看出,由于初始条件的设定,实际机器人的轨迹跟踪误差在仿真开始时变化较为剧烈,纵向位移误差ex和水平位移误差ey大约1 s后开始平稳变化,姿态角误差eθ在3 s后开始平稳变化,ex在5 s后收敛到0,ey和eθ在10 s后收敛至0.从图6可以看出,实际机器人在开始阶段逐渐加速,并利用较大的转向角速度迅速调整自己的位置,大约在10 s后达到参考机器人的行驶速度与转向角速度,并在以后的时间内一直保持一致.

图4 直线轨迹跟踪曲线Fig.4 Trajectory curves of the straight line trajectory tracking control

图5 直线轨迹跟踪误差曲线Fig.5 Error curves of the straight line trajectory tracking control
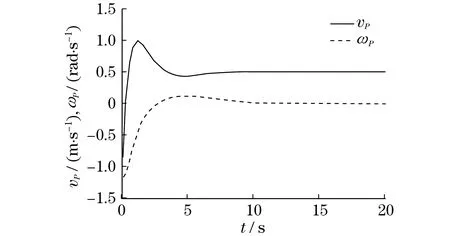
图6 直线轨迹跟踪控制输入曲线Fig.6 Control input curves of the straight line trajectory tracking control
3.2.2圆形轨迹跟踪仿真实验
设置参考机器人的初始位置和姿态角为(2, 0, 0.5π),行驶速度为1 m/s,转向角速度为0.25 rad/s;设置实际机器人的初始位置和姿态角为(2.5, 1, 0.75π),行驶速度为0 m/s,转向角速度为0 rad/s;轨迹跟踪控制器的参数为K1=1.0,K2=1.5,K3=1.2;仿真时间为24 s.圆形轨迹跟踪仿真实验的轨迹曲线、误差曲线和控制输入曲线分别如图7、图8和图9所示.

图7 圆形轨迹跟踪曲线Fig.7 Trajectory curves of the circle trajectory tracking control

图8 圆形轨迹跟踪误差曲线Fig.8 Error curves of the circle trajectory tracking control
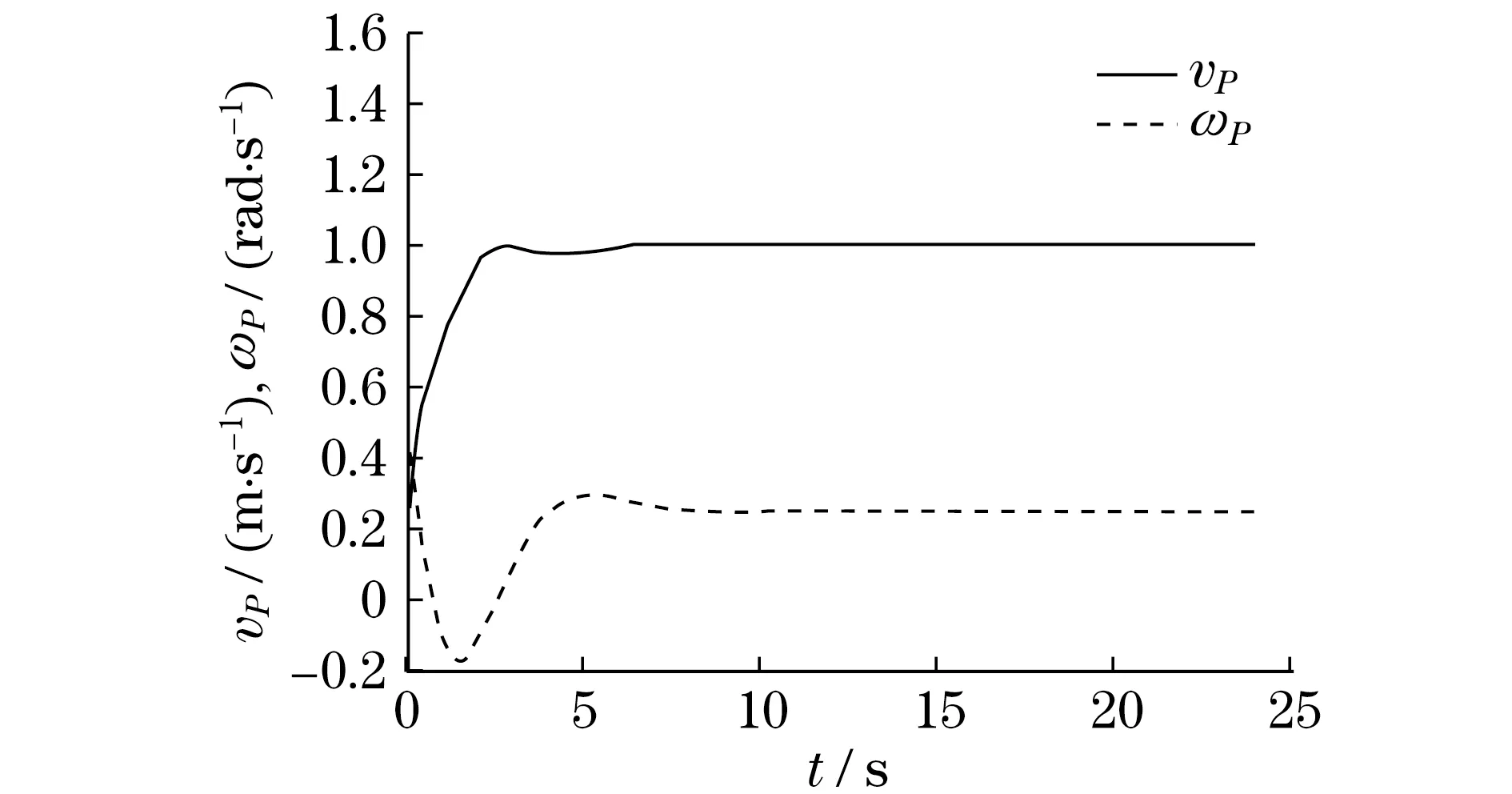
图9 圆形轨迹跟踪控制输入曲线Fig.9 Control input curves of the circle trajectory tracking control
从图7可以看出,参考机器人的期望轨迹是一个圆形曲线,实际机器人在仿真开始时具有一定的轨迹跟踪误差,但是经过轨迹跟踪控制后,实际机器人与参考机器人的轨迹重合.从图8可以看出,同样由于初始条件的设定,实际机器人的轨迹跟踪误差在仿真开始时变化较为剧烈,纵向位移误差ex和姿态角误差eθ大约1 s后开始平稳变化,水平位移误差ey在3 s后开始平稳变化,ex在5 s后收敛到0,ey和eθ在8 s后收敛至0.从图9可以看出,实际机器人在开始阶段逐渐加速,并利用较大的转向角速度迅速调整自己的位置,大约在8 s后达到参考机器人的行驶速度与转向角速度,并在以后的时间内一直保持一致.
从上述仿真结果可知,本文所提出的控制律能够快速地实现履带式移动机器人的直线轨迹跟踪与圆形轨迹跟踪,控制过程较为平稳,具有可实现性和有效性.
4 结语
本文首先提出了履带式移动机器人的运动学模型和轨迹跟踪动态误差模型.然后,基于Lyapunov稳定性理论,提出了一种状态反馈控制律,通过进行稳定性分析证明了该控制律能够实现轨迹跟踪的控制目的.最后为了评估所提出控制律的性能,在Matlab/Simulink环境下,分别进行了直线轨迹跟踪和圆形轨迹跟踪仿真实验.仿真实验结果证明,即使在给定了初始状态与初始误差的条件下,所设计的控制律仍然能够快速地实现直线轨迹跟踪与圆形轨迹跟踪,证明了所提方法的有效性和可实现性.本文所提出的方法具有良好的控制效果,能够保证控制过程的准确性与稳定性,可以广泛应用在履带式移动机器人轨迹跟踪控制的实际项目中.
参考文献:
[1] 杜孝平,赵凯琪.基于PID的移动机器人运动控制系统设计与实现[J].通信学报,2016(S1):43-49.
DU X P,ZHAO K Q.Design and implementation of the motion control system of the mobile robot based on PID[J].Journal on Communications,2016(S1):43-49.
[2] 郝存明,张英坤,梁献霞.基于滑模控制的室内移动机器人路径跟踪[J].计算机测量与控制,2017,25(8):93-96.
HAO C M,ZHANG Y K,LIANG X X.Path tracking of indoor mobile robot based on sliding model control[J].Computer Measurement and Control,2017,25(8):93-96.
[3] 吉洋,霍光青.履带式移动机器人研究现状[J].林业机械与木工设备,2012(10):7-10.
JI Y,HUO G Q.Research status of track-type mobile robots[J].Forestry Machinery and Woodworking Equipment,2012(10):7-10.
[4] 缪志强.自主移动机器人运动控制与协调方法研究[D].长沙:湖南大学,2016.
MIAO Z Q.Research on motion control and coordination for autonomous mobile robots[D].Changsha:Hunan University,2016.
[5] 杨涛.移动机器人轨迹跟踪控制[D].西安:西安电子科技大学,2014.
YANG T.Tracking control of mobile robots[D].Xi’an:Xidian University,2014.
[6] 吴剑,黄晓娟,江维.基于Back-stepping的轮式机器人轨迹跟踪[J].南昌航空大学学报(自然科学版),2012,26(4):89-93.
WU J,HUANG X J,JIANG W.Trajectory tracking for wheeled robot based on Back-stepping[J].Journal of Nanchang Hangkong University (Natural Sciences),2012,26(4):89-93.
[7] PARK B S,YOO S J,JIN B P,et al.Adaptive neural sliding mode control of nonholonomic wheeled mobile robots with model uncertainty[J].IEEE Transactions on Control Systems Technology,2009,17(1):207-214.
[8] FATEH M M,FATEH S.Fine-tuning fuzzy control of robots[J].Journal of Intelligent and Fuzzy Systems,2013,25(4):977-987.
[9] 范其明,吕书豪.移动机器人的自适应神经网络滑模控制[J].控制工程,2017,24(7):1409-1414.
FAN Q M,LYU S H.Adaptive neural network sliding mode control of mobile robots[J].Control Engineering of China,2017,24(7):1409-1414.
[10] CAI Y,GAO F,LIU Z N.Neural network compensation method for path tracking control of a spherical mobile robot[J].Applied Mechanics and Materials,2014,635/636/637:1325-1328.
[11] FRANKLIN G F,POWELL D J,EMAMI-NAEINI A.Feedback control of dynamic systems[M].5th ed.Englewood Cliffs,NJ:Prentice Hall,2006.
[12] SLOTINE J J E,LI W.Applied nonlinear control[M].Englewood Cliffs,HJ:Prentice Hall,1991.

