基于双谱能量算子的碰摩转子故障特征提取
(华北电力大学 机械工程系,河北 保定 071003)
旋转机械的转子部件在发生碰摩故障时,轴系会产生不规则、不稳定的振动,同时伴有非线性相位耦合现象,严重时会对机组产生危害.传统的傅里叶分析是建立在信号平稳的、高斯的假设之上,能够统计描述高斯过程,却不能获得高斯性的偏斜度和非线性的存在信息,无法处理非最小相位系统和非高斯信号[1].
相比于功率谱分析,高阶统计量分析能够获得信号高斯性的偏斜度和非线性存在信息,可以更加有效地描述和反映非线性系统所呈现的特征.双谱是高阶统计量中阶次最低、计算最简单的方法,可以表征信号的非线性相位耦合.2000年,Parker等[2]提出了基于双谱的诊断策略,并成功地应用于旋转机械的故障诊断.2007年,Kim等[3]通过理论和实验分析提出了一种基于双相干系数的二次相位耦合检测方法.在国内,双谱方法与其他方法结合的研究比较活跃.李辉等[4-5]提出了基于阶次双谱和倒双谱分析方法,对齿轮箱故障进行了诊断.朱忠奎等[6]提出了循环双谱表示方法,并验证了该方法在表示齿轮箱故障诊断中的有效性.杨少奇等[7]应用双谱分析和分形维数进行雷达欺骗干扰识别.蒋永华等[8]应用经验模态分解和双谱分析对滚动轴承的故障特征进行提取.国内外很多研究成果表明,双谱对齿轮和轴承等部件的故障比较有效,但对于转子碰摩故障的应用则较少.实际上,转子发生碰摩故障时,振动信号会表现出一定的非线性,且与故障的程度有关.对于早期故障,信号所包含的故障信息微弱,且极易被噪声淹没,故传统双谱方法对于碰摩故障的诊断能力较差.
转子系统的监测一般是在同一测点架设两个相互垂直的传感器进行测量,单通道双谱分析一般是将两路信号分别进行求取双谱,通过进行相似性比较来提取故障特征.实际转子系统的轴承在X,Y方向上的刚度、阻尼及等效质量是各向异性的.在转子发生碰摩故障时,支承的各向异性对转子稳定性产生的影响更加明显,而且碰摩故障的特征信息不一定出现在频率的对角线上,因此,采用双谱切片方法不足以全面、准确地反映转子的故障特征.李中原[9]、李凌均等[10]等进一步研究了基于双通道数据融合的矢谱分析方法,提出了矢双谱诊断方法,研究了矢双谱算法的设计和简单应用,但并没有给出应用矢双谱算法获取到的有价值的碰摩故障特征.
本文应用矢双谱处理转子全周碰摩数据,发现碰摩故障特征并不明显.为此,在矢双谱分析方法的基础上,结合Teager能量算子法,提出了一种新的基于双谱能量的转子全周碰摩故障特征提取方法.通过转子实验台模拟全周碰摩故障,应用该方法获取到了全周碰摩故障的双谱特征,并给出了合理的解释,从而验证了该方法的有效性.
1 基于谐波融合的矢双谱法
设X,Y为转子某一测点截面相互垂直的两个方向,xk和yk(k=0,1,…,N-1)为X,Y方向上的离散时间序列,其傅里叶变换分别为Xk和Yk.设Rxk,Ixk,Ryk,Iyk分别为Xk和Yk的实部和虚部,则信号xk和yk所包含的各谐波的幅值和相位可以表示为
(1)
式中:Axk,Ayk为k次谐波在X,Y向信号的振幅;φxk,φyk为k次谐波在X,Y向信号的相位.
k次谐波的幅值为
(2)
根据谐波融合方法[11]构造X,Y方向的融合信号
(3)
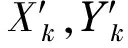
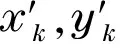
(4)
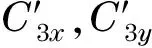
(5)
由于双谱的计算量较大,通常采用双谱切片来反映故障特征.在式(5)中令τ1=τ2=τ,则有
(6)
2 双谱能量算子
转子发生碰摩故障时,除了摩擦作用外还会产生冲击作用,其直观效应相当于给转子增加了一个瞬态激振力.Teager能量算子能够快速追踪信号总能量的变化,表征信号的瞬态能量特征,强化信号中的冲击成分[12],适合用于检测转子的碰摩故障.
对时间信号x(t)做Teager能量算子运算,符号记作ψC,简称为能量算子,计算方法如下:
(7)

假设窄带振动信号为
(8)
将v(t)代入式(7),则有
(9)
由式(9)可知,Teager能量算子输出为振动瞬时幅值与瞬时频率平方之积,相对于传统的能量定义,增加了频率项,由于瞬态冲击的振动频率较高,因此,Teager能量算子输出能有效增强瞬态冲击成分[13].
离散信号x(n)的Teager能量算子可定义为
(10)
为了应用Teager能量算子,提出了基于Teager能量算子的双谱能量算子法,用于碰摩转子的故障特征提取,具体步骤如下.
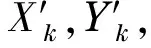

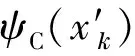
3 实验分析
为验证双谱能量算子法的有效性,在BENTLY NEVADA RK-4转子实验台上进行了实验验证.转子实验台的测试系统设置了两个测点测量轴振,每个测点在X,Y方向各架设一只电涡流传感器,如图1所示.

图1 BENTLY NEVADA RK-4转子实验台Fig.1 Test rig of BENTLY NEVADA RK-4
转子启动后,使转速上升至实验转速4 035 r/min(工频为67.25 Hz)并保持稳定,采用塑料棒与转轴进行接触,模拟单跨转子定转速全周碰摩故障,数据采集系统进行同步整周期采样,采样频率为1 280 Hz,采集到的时域信号如图2所示.
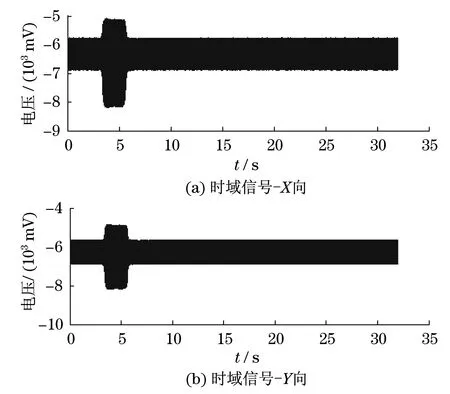
图2 转子碰摩的时域信号Fig.2 Vibration signals of rubbing rotor
由图2可知,碰摩发生时刻约为3.3 s处,碰摩结束时刻约为5.6 s处.分别截取转子正常和碰摩状态下的振动数据,数据长度为2 048点,按式(1)~式(5)计算矢双谱,所得结果如图3和图4所示.
由图3和图4可知,正常转子和碰摩转子的矢双谱在低频区基本一致,而高频区杂乱无章,且双谱数值较小,无法提取到有用的故障信息.此外,根据X,Y向数据分别得到的矢双谱在高频段也有明显差异,实际诊断中应选择哪一个方向的数据也缺乏理论依据.由此可知,虽然矢双谱融合了双通道数据,理论上所包含的信息更加充分,但在低频段没有表现出对碰摩故障的诊断能力.
将上述数据按双谱能量算子法处理,所得结果如图5和图6所示.由图5和图6可知,基于能量算子的矢双谱,X,Y两向处理结果基本一致,实用中只需取其中一个方向即可,避免了矢双谱方向选择的问题.
通过比较图5和图6的处理结果,正常转子和碰摩转子在低频段存在明显差异,碰摩数据所得的双谱能量算子,在归一化频率(0.053,0.156)处具有最大的数值,对应的信号频率为(67.84 Hz,199.68 Hz);其次是归一化频率(0.053,0.104)处的双谱值也很大,对应的信号频率为(67.84 Hz,132.51 Hz).发生的二次相位耦合的位置,位于转子工频的1,2倍频和1,3倍频处,而正常转子在此两位置上不发生二次相位耦合,此特点可以作为碰摩转子的故障特征.
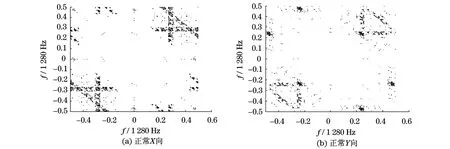
图3 正常转子矢双谱Fig.3 Vector-bispectrums of normal rotor
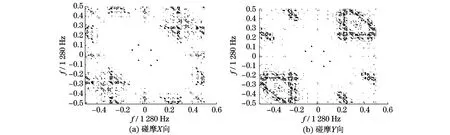
图4 碰摩转子矢双谱Fig.4 Vector-bispectrums of rubbing rotor
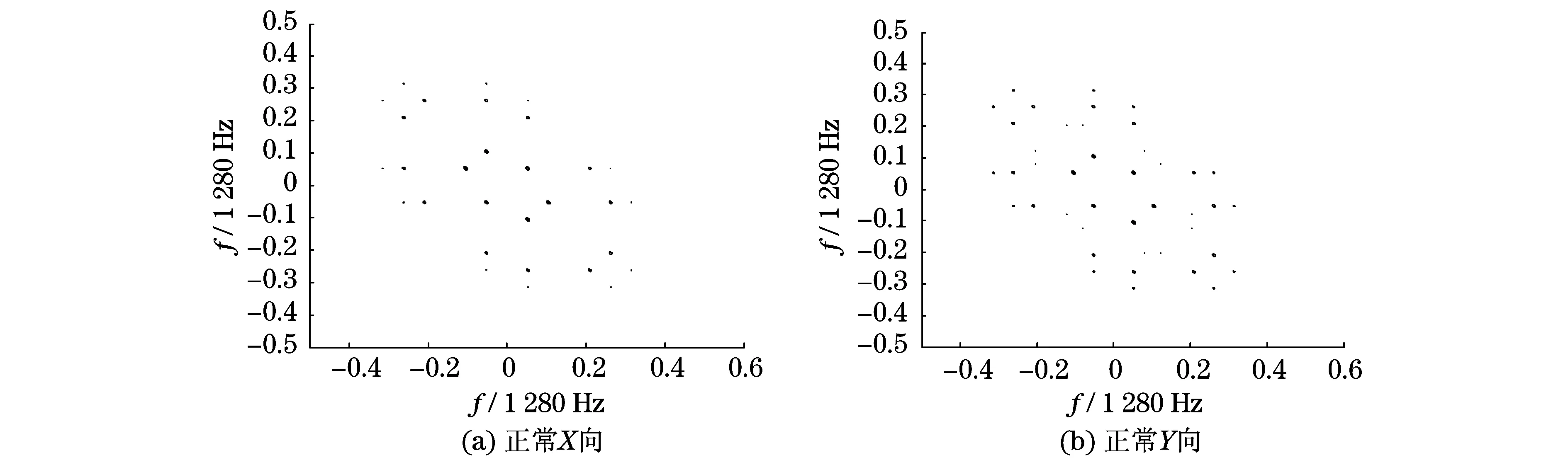
图5 正常转子双谱能量算子Fig.5 Bispectrum energy operators of normal rotor
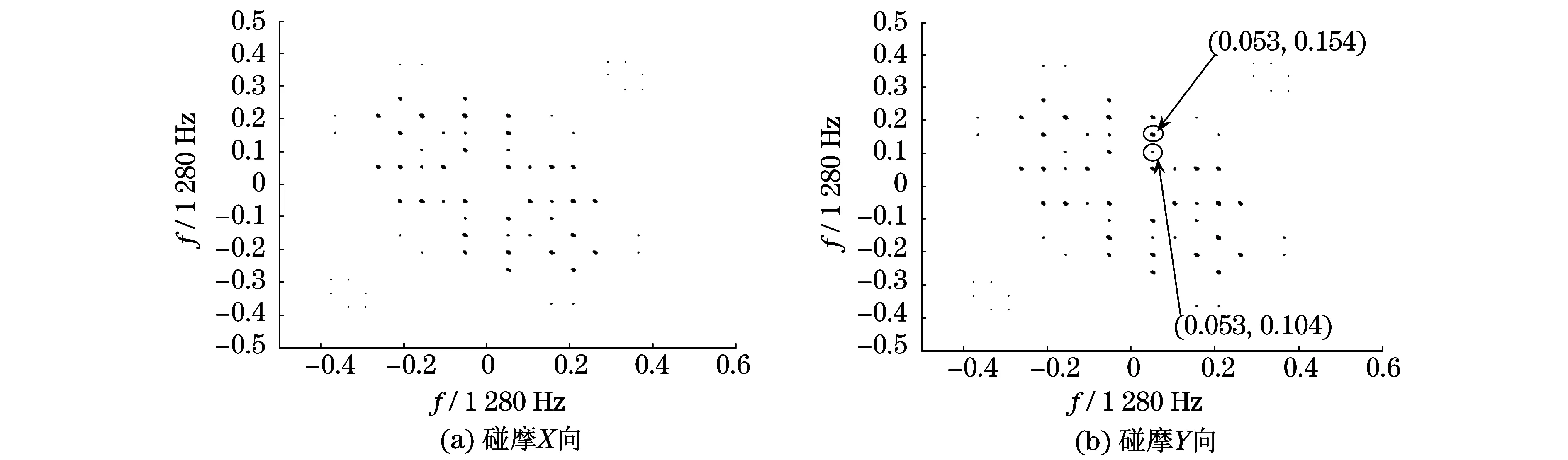
图6 碰摩转子双谱能量算子Fig.6 Bispectrum energy operators of rubbing rotor
4 结论
发生碰摩故障的转子从严格意义上来讲是非线性系统,其振动信号是非平稳的,并存在二次相位耦合现象.研究发现,矢双谱分析方法能够抑制信号中的高斯噪声,分析二次相位耦合成分,但矢双谱对于碰摩故障的特征提取存在着丢失故障特征的问题,数据方向的选择也缺乏理论依据.
针对这一问题,本文提出了基于双谱能量算子的碰摩转子故障提取新方法,并进行了实验研究.结果表明,基于能量算子的双谱能量分析方法继承了矢双谱的优良特性,充分融合了双通道信息,比矢双谱反映的信息更加全面.通过对转子碰摩数据的处理发现,双谱能量算子法所得到的两个方向处理结果是一致的,实用中可任选一个方向进行分析,从而解决了矢双谱的数据选择问题.此外,基于能量算子的双谱能量分析方法能明确区分正常转子和碰摩转子,当转子发生碰摩故障时,信号频率成分向高频区扩展,发生二相位耦合的故障信息在1,2倍频和1,3倍频处.
参考文献:
[1] 郑海波,陈心昭,李志远.基于双谱的齿轮故障特征提取与识别[J].振动工程学报,2002,15(3):354-358.
ZHENG H B,CHEN X Z,LI Z Y.Bispectrum based gear fault feature extraction and diagnosis[J].Journal of Vibration Engineering,2002,15(3):354-358.
[2] PARKER J B,WARE H A,WIPF D P,et al.Fault diagnostics using statistical change detection in the bispectral domain[J].Mechanical Systems and Signal Processing,2000,14(4):561-570.
[3] KIM T,POWERS E J,GRADY W M,et al.A novel QPC detector for the health monitoring of rotating machines[C]//Proceedings of 2007 IEEE Instrumentation and Measurement Technology.2007:1-6.
[4] 李辉,郑海起,唐力伟.基于阶次双谱分析的齿轮故障诊断研究[J].应用基础与工程科学学报,2007,15(3):351-356.
LI H,ZHENG H Q,TANG L W.Gear fault diagnosis based on order bispectrum analysis[J].Journal of Basic Science and Engineer,2007,15(3):351-356.
[5] 李辉,郑海起,唐力伟.基于倒双谱分析的轴承故障诊断研究[J].振动、测试与诊断,2010,30(4):353-356.
LI H,ZHENG H Q,TANG L W.Application of Bi-cepstrum technique to bearing fault detection[J].Journal of Vibration,Measurement and Diagnosis,2010,30(4):353-356.
[6] 朱忠奎,孔凡让,王建平,等.循环双谱及其在齿轮箱故障识别中的应用研究[J].振动工程学报,2004,17(2):224-227.
ZHU Z K,KONG F R,WANG J P,et al.Study on the applications of cyclic bispectrum in gearbox fault diagnosis[J].Journal of Vibration Engineering,2004,17(2):224-227.
[7] 杨少奇,田波,周瑞钊.应用双谱分析和分形维数的雷达欺骗干扰识别[J].西安交通大学学报,2016,50(12):128-135.
YANG S Q,TIAN B,ZHOU R Z.A jamming identification method against radar deception based on bispectrum analysis and fractal dimension[J].Journal of Xi’an Jiaotong University,2016,50(12):128-135.
[8] 蒋永华,李荣强,焦卫东,等.应用EMD和双谱分析的故障特征提取方法[J].振动、测试与诊断,2017,31(2):338-342.
JIANG Y H,LI R Q,JIAO W D,et al.Feature extraction method based on empirical mode decomposition[J].Journal of Vibration,Measurement and Diagnosis,2017,31(2):338-342.
[9] 李中原.旋转机械矢双谱分析及故障诊断应用研究[D].郑州:郑州大学,2006.
LI Z Y.Application research on vector-bispectrum analysis and fault diagnosis in rotating machinery[D].Zhengzhou:Zhengzhou University,2006.
[10] 李凌均,韩捷,李朋勇,等.矢双谱分析及其在机械故障诊断中的应用[J].机械工程学报,2011,47(17):50-54.
LI L J,HAN J,LI P Y,et al.Vector-bispectrum analysis and its application in machinery fault diagnosis[J].Journal of Mechanical Engineering,2011,47(17):50-54.
[11] 韩捷,石来德.全矢谱技术及工程应用[M].北京:机械工业出版社,2008.
HAN J,SHI L D.Full vector spectrum technology and its engineering application[M].Beijing:Mechanical Industry Press,2008.
[12] 唐贵基,王晓龙.基于EMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J].振动与冲击,2014,33(1):6-10.
TANG G J,WANG X L.Fault diagnosis for roller bearings based on EEMD de-noising and 1.5-dimensional energy spectrum[J].Journal of Vibration and Shock,2014,33(1):6-10.
[13] 马增强,李亚超,刘政,等.基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J].振动与冲击,2016,35(13):134-139
MA Z Q,LI Y C,LIU Z,et al.Rolling bearings’ fault feature extraction based on variational mode decomposition and Teager energy operator[J].Journal of Vibration and Shock,2016,35(13):134-139.

