巧用天平纠正等号认知的误区
□ 竺新波
【问题回顾】
一天,一(6)班的琪琪拿着作业本走进办公室,怯生生地说:“竺老师,我觉得这里是对的!”我看了一眼,见她指着《加法的认识》随堂练习的“3=①-④”这题,我就小声地把课堂上讲过的又和她讲了一次:“算式是从左往右读的,你这样写就变成1-4等于3了!”琪琪似懂非懂地走了。这时,同年级组的费老师说:“这道题我们班也错了很多,三分之二的人都错的!我明明强调了好多次,可很多孩子就是写不对!”是啊,我们班也是这样,孩子为什么认为“3=1-4”是对的呢?
我把错题写在了纸上,像琪琪这样的孩子应该错在了从右往左读这个算式,即4-1=3。仅仅是左右不分的问题吗?但是,从左往右读算式这样的读法似乎在教材里面找不到根据。既然是一个等式,等于号左右两边都相等,那么从右边看到左边这样的思考方式也是对的。我盯着数字中间的“=”,突然想到,问题在这里,是孩子没搞懂这个等于号!
为了证明我的思考是正确的,我在还没有上“认识大于小于和等于”这一课的一(1)班作了一次测验(我们采用年级组集体备课的方式,虽上课进度不同,但授课环节相同,根据测试结果也可推断本班孩子的情况)。

结果还不错,正确率达75%,其中要填写“=”的3、6两题正确率达到了100%。显然孩子们非常清楚“两边一样用等号”这一知识。
在学习了《加法的认识》之后,我又进行了测验。

分析测试结果,我发现“4=□+□”和“3=□-□”,出错较普遍,“3=□-□”错误率更是高达75%。
孩子明明清楚“=”表示两边一样,但碰到数和式的练习时却出现了偏差,的确匪夷所思,但细细思索,却也能找到合理的解释。
首先,在入学前家长会教给孩子简单的加减法,如2+3=5,10-3=7等,孩子练习了大量的算式,这些练习给了孩子一个非常强烈的信号:等号就是从左往右得出结果。所以,孩子眼中的等号其实只是得出结果前的过渡符号,它的作用和“→”是一样的。
其次,教师在教学时并没有意识到孩子的片面认识。等号的本质是表示左右两边相等,但无论是教材还是我们的课堂教学,都不能给孩子相应的体验。我们总是把教学重点放在认识新面孔“>”“<”上,甚至认为孩子在之前的经验中已经认识了“=”。殊不知,他们在计算式子在前数字在后的题目时(如2+5=7),把等于号当作“→”,而在见到数字在前式子在后的题目时,如得出3=1-4,自然而然地把等于号当作“←”。
再次,据皮亚杰的研究,儿童是从前运算期(大约在6~7岁)开始直到具体运算期(大约在11~12岁)才逐渐地形成逆向思维和平衡观念。如果把类似“2+5=□”这样的算式看作是顺向思维,那么在“3=□-□”的解决问题过程中是需要逆向思维和平衡观念参与的,这对一年级的孩子来讲的确是一个挑战。
【教学建议】
那么,在有限的课堂教学中,如何让学生认识等号表示两边相等的真正含义呢?
一、找准联系,使等号认知系统化
建构主义理论指出:在学习过程中帮助学生建构意义,就是要帮助他们对当前学习内容所反映的事物的性质、规律以及该事物与其他事物之间的内在联系达到较深刻的理解。大于、小于和等于号,这三个符号的共通点就是非常形象地揭示了左右两边的关系:两边一样大就开口一样大,大口朝大的那一边。
【案例1】
1.认识“=”
师:神奇的数王国的大街上发生了争吵,它们是谁呢?
师:小朋友,你说说到底谁大呢?
生:5和5同样大。
师:你可以用一个记号表示同样大的意思吗?
生:等于号。
书写等号:等号两边一样长,一样平,开口一样大。
2.认识“>”
师(出示5=5):如果左边是6,等于号还可以用吗?
(课件动态演示把等于号变成大于号:本来两边开口一样大,大数的那端口变大,另一端变成尖)
3.认识“<”
师(出示5=5):如果把5变成4,该用什么符号呢?(动态出示小于号)
【思考】一般的课堂设计中,教师会带领学生认识两个新符号,教他们要记住“大口朝大数”。案例中,用课件演示的方式,直观地告诉学生大于号、小于号是通过等于号变化而来的,即“两边相等开口相同,两边不等大口朝大数”,明确了三个符号的系统关系。
二、巧用天平,使等号认知形象化
对以形象思维为主要形式的学生进行抽象的符号教学时,还需要借助更加直观、形象的载体。天平和学生经验中的跷跷板有相通之处,当两边一样重的时候,天平是平的,就像等号一样,当哪边重的时候,天平就会向哪边倾斜。天平能使等于这个符号更形象更直观地植入学生的心中。
【案例2】
教师在黑板上画了一个天平。

师:要使天平保持平衡,而且这两个数字宝宝不能拿下来,你有什么办法呢?
生:3那里再加一个5。(板书:8=3+5)
生:8那里减掉5。(板书:8-5=3)
师:如果把8和3换个位置呢?
……
【思考】这样的设计旨在告诉学生:等式的两边犹如天平的左右两边,两边的数值相等,位置也可以左右互换。使“8=3+5”这种数字在左式子在右写法的出现不再突兀,而且清楚地告诉学生“3=8-5”等式的来历,进而避免出现前文“3=1-4”类似的错误。
三、丰富素材,使等号认知深刻化
对比各版本教材,对于□=□○□这种“逆向”的算式模型,在新课中没有提及,即使在练习中也出现得较少,缺少反复的认知刺激也是学生易错的原因。课堂教学中应该提供丰富的素材,使学生对等号的认识更加深刻。
【案例3】
在学习“认识大于、小于和等于”后可以补充如下素材进行练习。
○中该填写哪个符号?
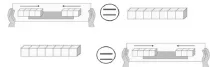
【思考】用更加直观的图解,使学生更准确地理解等号的意义。
学习了“加法的认识”之后,也可以再次进行等号的复习。

师:你能用4+3说一说每一幅图画的意思吗?
【思考】这四幅图中,看似都是简单的加法运算,其实右上天平图揭示了等号的含义,对于等号的认知颇具练习价值:左边小马身上的“7”,是和右边的“4”和“3”加起来一样大的。
就这样,笔者不断在平常的教学中进行“=”的认知训练,在期末复习中,笔者特意设置了类似易错习题,结果令人欣喜,40个学生完全避免了“3=1-4”这样的错误。

