方式多样，让课堂学习活动的展开过程走向丰盈*

□ 蒋敏杰

学生数学思维能力的提升，无论是学习方式的丰富，还是教学方式的优化，仍需注重对于课堂学习的价值定位，即要有围绕学习内容的、体现数学学科特质的、高质量互动发展的教学“过程观”。如何让课堂教学展现“过程”，体现“学习活动”的丰富意义呢？教学实践表明，散点的目标预设，线性的思维问答，机械的师生互动，局部的内容理解，是阻碍学生在课堂中体验丰富的学习过程、增进学习体验的主要原因。完全在教师预设控制下的知识学习，不会产生积极的、丰富的学习感悟，只能让学生产生数学学习无非是记公式、算题目以及想不完、道不明的解法等错误认知。

促进学生数学学习中的思维发展，需要注重动态学情的把握，理解教材内容及编排特点，顺应儿童当下的思维特点与认知经验，通过具有挑战性的问题引领，使学生经历丰富的思考与实践体验，获得对自我数学学习的认识，提升信念，形成方法，从而促进儿童数学核心素养的培育与完善。

一、结构化内容连接，提升整体感知

奥苏伯尔“先行组织者”理论对基于方法联系下的知识学习，提出了“比较性组织者”。其意图就在于通过结构相近、思维方式相似的问题引领，让学生主动对将要解决的问题中蕴含的具体思维进行回顾表征，唤醒其认知经验中对问题的连贯性的结构思考。准确把握教材内容体系，从学生的学习问题（困难）及意义链接处入手设计活动，有助于学生在后续问题分析中，形成相对完善的认识方法。基于此，数学教师在自我理解及引导学生理解教材内容时，应突破局部的“点”的认识，通过对数学内容“生长点”与“延伸点”的分析，帮助学生在回顾与整理中，突出内容之间的实质联系，帮助学生进行共性化思考。

比如，长度概念、面积概念、体积概念在认知方式上存在着结构关联，每次教学都是对认知方法的进一步完善。在教学中，教师顺应学生的认识层次，为学生深入感知理解提供方法支撑，并形成相应的研究路径与方式。在对体积概念的引领认知时，可以设计如下活动唤醒与勾连相关经验。

T：二年级的时候我们学习了长度，认识了线段，知道线段是由无数个点形成的；三年级的时候我们又研究了面积，知道由无数条线段叠加在一起可以形成面。在长度、面积的学习中，我们是怎样来认识它们的呢？想一想，它们有什么共性的地方？（学生交流、相机板书）

T：连点成线、以线成面，那么面的运动形成什么呢？（动画演示，引出：体）它又可以从哪些方面进行研究？今天我们就继续来研究“体”。

除了考虑知识间的纵向联系外，还可以从知识发展的横向联系入手进行分析，形成网状结构。更为重要的是，教师要学会从儿童的思考角度规划学习的过程，找到学习经验与内容的横向发展联系，帮助学生通过学习探究，感受到一类问题的解决途径。比如苏教版小学数学教材①本文中的教材内容均为苏教版义务教育小学数学教材，后简称为“教材”。中《乘法分配律》的教学，教师需立足“运算律”单元，横向沟通各运算律探究方式与思维过程的联系，整体设计过程与方法，不断丰富学生“观察现象—提出猜想—丰富例证—沟通应用”的思维路径，体验从特殊到一般的抽象过程，进而实现内容、方法的同步自主内化与建构。“知其然，知其所以然”，引领学生学会对数学问题进行结构关联的合理思考。

二、立体化过程推进，促进方法延伸

丰富多元的数学学习活动，也要关注活动的“品质”，也就是通过学习活动的持续、深入地推进，不只是同一层次的重复，还要不断引导学生对自身原有知识体系进行调整、重组与补充，带动学生在思维节点处“发散”与“聚类”，实现思维内容与方式的横、纵向延伸。这种状态下，活动设计除了关注“知识”之外，更强调学生知、情、意、行的协作发展，促进“方法”的延伸，体现课堂中学生思维的真实发展。

比如“异分母分数加减法”教学中，教师呈现

T：你能独立解决这个问题吗？想一想，可以怎样来计算，求出结果。教师巡视，收集学生资源。

第一种通分，将异分母分数化成同分母分数就

第二种化成小

T小结：同样的一个计算问题，可以分析数据的特点，利用通分，化成同分母分数进行计算，也可以根据分数的特点，化成小数计算，从多种不同的思维路径解决问题。

T：想想分别可以用哪些方法来解决？试着简要地写一写。

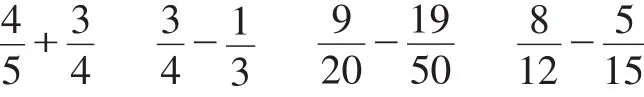
学生进行分析并计算后，教师组织横向比较交流。

T：为什么择通分？（无法化成有限小数） 为什多种通分方法？哪种更合理呢？

追问1：为什么这4个异分母计算，大家在方法应用上有差异？

追问2：通过上述计算，对你在计算上有什么启示，有什么经验可与同学分享？

T小结：同样是通分，还要根据数据的特点，选择合适的方法。有时先约分后再通分能使计算简便。

上述过程，通过教师的横、纵向比较分析，突出了“结合数据特征，合理选择算法”的运算能力培育。在“分析数据、选择算法、比较优化”的多样化问题情境下，师生的学习活动不断深入，推动了学生数学思维的提升。

上述例子展现的是一堂课的递进，同样，一类知识与方法的整体感悟，更需要教师有意识的引导，使学生认识到内容的联系。比如“三角形面积计算”教学，教师要从“单元”视角，整体把握三角形与平行四边形面积计算推导、梯形面积之间研究方式的共通性，增强研究方法结构的联系体验。向上追寻平行四边形面积计算的研究过程，向下拓展梯形等平面图形的研究方式，进而帮助学生丰富“想转化—找关系—推公式”的研究路径。如此，研究方法与实践经验将在主动探索中不断内化与拓展。

三、有向的思维互动，实现思维联动

结构的意义感知基础在问题，核心在问题的深入推进。数学课堂教学中，要让学生体验与经历丰富的数学活动过程，教师要细致地将知识、技能等聚成一个个的问题链，借助有向思维引导，指向明确的问题根源，有效触动思维活动，达成对数学现象的剖析理解，最大程度帮助学生聚焦现象、发现规律、寻求答案。同时，在这个过程推进中，教师要依据学习进程动态地捕捉资源，灵活调整教学进程，生成新的教学环节，将课堂学习活动不断进行新的拓展。

比如，在“平均数”教学中，把“平均数”的认识环节，设计成师生互动、个性表达的过程，能有效地促进学生思维的发展。

T：通过同学们刚才的分析，我们一致认为，直接比较总数与比较最大值都不能作为比较甲、乙两队完成情况的方法。同学们建议先分别求出甲、乙两队平均每个人完成多少块，再进行比较。

甲队 乙队

T：怎么求出两队的平均数？（四人小组讨论，推选一位学生介绍学习成果）

学生反馈：哪个小组来汇报一下？

估算：我们组估计一下，如果要使他们同样多，甲队大概在5块左右，乙队大概在4块左右……

平均数的范围：最小数＜平均数＜最大数

移多补少方法：对估算方法的验证延伸出来。电脑呈现：我们一起来估算一下（把一根水平线移到7的位置），平均数会是7吗？为什么？……

计算：

甲队（7+3+5）÷3=5（块）

乙队（2+7+3+4）÷4=4（块）

T：你是怎么想的？5代表什么？4代表什么？

T：和小李的5一样吗？和小风的4块一样吗？（这种数字相同纯属巧合）

T：平均数跟以前学过的每份数一样吗？（实质不同。呈现每份数的条形图和平均数的条形图作对比）

T总结：总数量÷总份数=平均数。

可以看到，学生对于平均数的意义理解，形成于师生的协作探索中，由意会而至言传，在对比中清晰概念意义、深刻理解概念。因此，数学课堂中师生交流的聚焦程度决定着学生思维的品质，师生互动结构越清晰，指向于核心问题就越精准，越切合于问题核心，学生思维内容的整体架构也就更为合理与完善。

四、个性化反省优化，增强意义链接

学生在学习过程中所获得的经验，有的是显性的、可感的，有的是内隐的、抽象的，而往往是那些隐性的经验会给学生带来意想不到的发展。教学中促进学生思维提升，需要不断增强学生对自我学习的认知，对学习内容的自我理解，对学习方法的个人认同。这些都需要教师在课堂教学中，有意识地通过回顾完善环节，帮助学生经历元认知过程，增强意义链接。

例如，在复习六年级“平面图形的面积”时，当学生对平面图形面积的计算经历了自主梳理、小组交流，形成初步结构后，教师要及时抓住思维节点，通过课堂互动交流，帮助学生在思维策略上实现反思完善。

T：这些平面图形的面积怎样计算？可以怎样推导得出？在推导过程中运用了哪些策略？（平移、旋转、化曲为直等转化策略）

T：为什么将这些平面图形按这个结构层次来安排，它们之间有哪些联系？你认为哪个图形是关键？

T：在这次梳理结构中，你遇到了哪些挑战，你是如何解决的？你最大的收获是什么？

在这组问题交流中，教师主要抓两个核心：其一是结构关联，即为什么这样来梳理，如何体现知识联系，指导学生注重知识间的内在联系，通过变与不变的分析，实现对平面图形计算的整体架构；其二是思维反省与完善，着力体现个人对学习过程的反省，帮助学生有意识地感悟方法，积累经验。

总之，教师围绕学习内容，合理规划学习活动的展开过程，设计学习任务，丰富学习研究方式，将有效推动学生的数学研究与发现。带着思考去观察与发现，丰盈数学课堂学习活动的展开过程，是提升学生思维的重要路径，将赋予学生发展的更大可能。