中国股债市场的非对称联动效应分析——基于PVAR的方差分解模型

郭 娜 李俊希

一、引言

股权融资和债权融资是一般企业进行资金融通的两种主要直接融资方式，对股债联动效应的研究有利于发现二者之间的内在关联，促进通过跨市场交易来优化资源配置，从而从内生动力上进一步深入贯彻落实党的十九大及全国金融工作会议强调的提高直接融资比重的会议精神。

大多数企业为维持一个高效率的资本结构，会选择同时发行股票和债券，当一家企业经营状况、财务报表、股东变革等发生变化时，这些相关信息会同时影响该企业发行的股票和债券的价格，也就是说，对于同一家企业的股票和债券而言，它们波动性的一部分可能是由同一种信息导致的，形成股债的信息传导及联动效应。但是，大量文献表明导致股票和债券波动的主要决定因素却大相径庭，因此，企业的股债之间具有怎样的联动效应？债股之间的风险是否会相互传导？这种传导作用是否为双向的？这些都是股票市场和债券市场中值得探讨的问题。

研究股债联动及其影响因素的文献，大多局限于几种传统的模型，如向量自回归模型、广义自回归条件异方差模型（GARCH）及 GARCH衍生模型和Copula模型等。简单地进行向量自回归虽能较好地描述变量间的动态关系，但系统中变量需要满足一定可回归的要求，GARCH模型虽适用于时间序列波动性的分析和预测，但在解释股票收益和收益变化波动之间出现的负相关现象稍显局限性。目前，针对收益率的研究相对较多，而关于收益波动率的研究仍属于开放性话题。一些文章中通过已知的变量为收益波动率给出统计学上可靠的解释，但考虑到预测变量的时间效应时，国外研究学者运用收益方差分解模型给出更有力的解释。最具代表性的是Campbell(1988）[1]提出线性估计资产定价模型，将股票超额收益分解为关于未来股票收益、股票分红及通货膨胀率的信息，并通过向量自回归中的残差信息获得分解因子的表达式，发现分红信息贡献主要的股票收益波动。此后Tom Engsted(2001）[2]将 Campbell(1988）[1]进行改进，并补充债券超额收益的分解表达式，发现通胀率是债券波动的主要驱动因素，同时探究了丹麦股票债券市场间的关系。

本文将首次运用权益方差分解模型代替传统衡量波动性的研究方法，来探讨股票收益波动性和债券收益波动性的联动特征，并综合我国学者发现对股债联动有影响的宏观因素，以及 Campbell(1988）[1]和Tom Engsted(2001）[2]所考虑的微观因素，通过多元回归来解释股债相关性。创新点在于，第一，将股债联动的研究对象从宏观上代表市场行情的指数序列转移到微观角度的多家上市企业的股票债券收益率的面板数据；第二，首次在中国股债市场中运用收益的方差分解模型并设计多元回归详细探讨股债联动的非对称特征及影响因素。

本文余下结构安排如下：第二部分，概括该课题的研究现状并从中找出创新点；第三部分，模型研究设计，参考Campbell的收益的方差分解模型分解股票与债券的非预期收益，根据相关文献，选择向量自回归模型的系统变量，利用VAR模型的残差构造收益方差和协方差序列，得到分解因子的表达式，然后分别进行分解因子方差和协方差序列的多元回归，分析联动是否具有非对称性以及影响联动的主要因素；第四部分，展示实证检验结果；第五部分，根据实证结果归纳结论，并提出相关建议。

二、文献综述

大量文献从股票指数和债券指数研究宏观市场行为，发现股票市场和债券市场一定程度上具有联动性，而联动的特征各占其词。王璐和黄登仕(2015）[3]在分割市场下引入R藤Copula模型构建多维金融市场联动模型来探讨两个股票子市场和两个债券子市场的交叉联动特征，结果表明联动性整体较弱，在下跌时股债联动性更强。郑振龙和陈志英(2011）[4]运用DCC模型发现股债相关系数是时变的，且大部分表现为正相关，同时发现股票市场的不确定性对股债相关性具有负作用。韩学红、郑妍妍和伍超明（2008）[5]研究发现整个样本期间实际股票收益率和通货膨胀率相关性不明显。同样处于供给冲击大于需求冲击的情况，两个不同时期子样本分别出现实际股票收益率和通货膨胀率负相关和正相关的结果。罗荣华、门明和吴锟（2014）[6]采用 t分布的DCC⁃MVGARCH模型来估计股票和债券收益率的动态相关系数，发现我国股债联动是非线性的。曾志坚和江洲（2007）[7]用自回归分布滞后模型（ADL）发现股票市场与债券市场月收益率之间不存在领先滞后关系，而日收益率之间债券领先于股票一天。从国内学者的研究贡献来看，我国股票市场和债券市场的联动性整体来看较弱，但具有时变性和非线性，某些时期表现出较强的相关性，某些时期相反。

而国外的情况似乎相反，Campbell和 Ammer(1993）[8]运用线性资产定价模型和向量自回归将股票收益和债券收益的联动分解，研究发现股票和债券的超额收益的方差之间具有较高的相关性。Tom Eng⁃sted和 Carsten Tanggaard(2001）[2]运用 Campbell和Ammer(1993）[8]的VAR及信息的方差分解模型，经过引导模拟调整误差后分析了丹麦股票和债券市场年度数据的联动情况，同样得出股债之间高度相关的结论；Aslanidis和Christiansen(2012）[9]基于高频数据运用平滑转换回归模型发现了股债相关关系及正负转换性；Bharat Kolluri等（2014）[10]运用多变量协整模型检验了印度的股票和政府债券市场的相互关系以及与美国，英国，日本，中国，和新兴市场股市之间的关系。结果表明印度的股票和债券市场由一个长期的协整关系联系在一起。

从股票和债券的相互影响方面来看，许多文献表明二者的作用可能是非对称的。徐林（2006）[11]研究发现国债市场对股票市场具有较大的影响力，而股票市场对国债市场的影响力十分微弱。刘大明(2012）[12]分别对全样本和子样本进行VAR和二元GARCH模型研究股票和债券相关性，发现全样本存在程度较低的相互影响关系，且债券对股票的影响作用大于股票对债券的影响作用，而子样本结果发现这种影响关系基本是对称的，并且联动具有时变性。陈学彬和曾裕峰（2016）[13]从股票和债券市场的尾部风险溢出效应角度出发，运用多元多分位数MVMQ⁃CA⁃ViaR模型发现中国股票和债券的极端风险传导效应在近年来得到加强，在牛市和熊市行情股债两市不具有显著的尾部风险溢出效应，而在震荡期表现出明显的风险溢出关系，并且股票市场对债券市场只具有单向的风险传导效应。

从已有的研究成果看来，绝大多数学者对股票市场和债券市场的联动性以及相互作用的非对称性的研究存在一些问题：第一，仅仅停留在宏观市场或指数的分析，鲜有文献针对每家企业的股票和债券之间的关系进行研究；第二，国内学者在研究股票债券关系时，大多直接运用收益率序列进行分析，国外一些学者却更重视收益率的方差序列，这也更能体现波动的特性。因此本文将运用Campbell(1993）[8]的方差收益分解模型来构造股票和债券收益率方差协方差序列，从微观角度来分析每家企业的股债面板数据之间的联动性以及非对称效应。

三、研究设计

（一）线性估计资产定价模型

我们通过线性估计资产定价模型来分析股票市场的基本特征。对数股票收益率st+1=log(Pt+1+Dt+1）-log(P）t，企业股票超额收益率et≡st-rt；以及股利收益率φt=dt-pt。Pt+1为t+1期的股票价格，pt为股票价格的对数，Dt+1为t期至t+1期的股利收益，dt为股利收益的对数。rt为t期的实际利率。将对数股票收益率进行一阶泰勒展开近似得到下列方程：

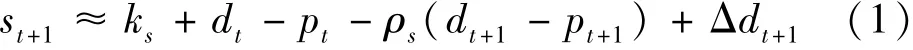
其中参数ρs=(1+exp(））-1，ks为常数，将方程(1）变形得到方程（2）

方程（2）表示对数股利收益率dt-pt可以被写成以ρs为贴现率的未来所有期的股票收益率st+i+1和股利增长率Δdt+i的折现值之和再减去常数ks/(1-ρs），将方程（2）取期望加以变形可得到下式

联立方程（1）～(3）可得到方程（4）和（5）

同理在债券市场中，定义债券收益率

其中ρb=exp(y-）-1和kb=-ρblog(ρb） -(1-ρb）log(1-ρb）为线性化过程中产生的常数，yt为t时刻的金边债券收益率，将方程（6）变形得：

定义企业债券超额收益xt+1≡bt+1-it≡bt+1-πt+1-rt+1代入方程（7）得方程（8），方程（9）为取期望形式

综合方程（6）～(9）可得方程（10）和（11）

（二）VAR及方差分解

根据 Campbell和 Ammer(1993）[8]以及 Tom Eng⁃sted和Carsten Tanggaard(2001）[2]的改进回归模型，构造向量自回归（VAR）来预测方程（5）和方程(11）右边的因素，VAR系统中的变量包括企业股票超额收益率et，企业债券超额收益率xt，实际利率rt，对数股利收益率φt以及连续复利利率的差分Δit，方程如下：

向量自回归模型可构建为：zt+1=Azt+ωt+1，A为VAR的系数矩阵，w为VAR的残差矩阵。为方便书写，将方程（5）和方程（11）简写为方程（13）和（14）形式：

并取方差可得到：

根据向量自回归的残差特点，企业股票超额收益率为VAR系统中第一个变量，因此，非预期的企业股票超额收益率即为VAR中第一个残差序列，同理，非预期的企业债券超额收益率为VAR中第二个残差序列，定义单位向量eiT=(0，…，1，…，0），根据(Et+1-Et）zt+i+1=Aiωt+1可以计算出方程（13）和(14）中各因子的表达

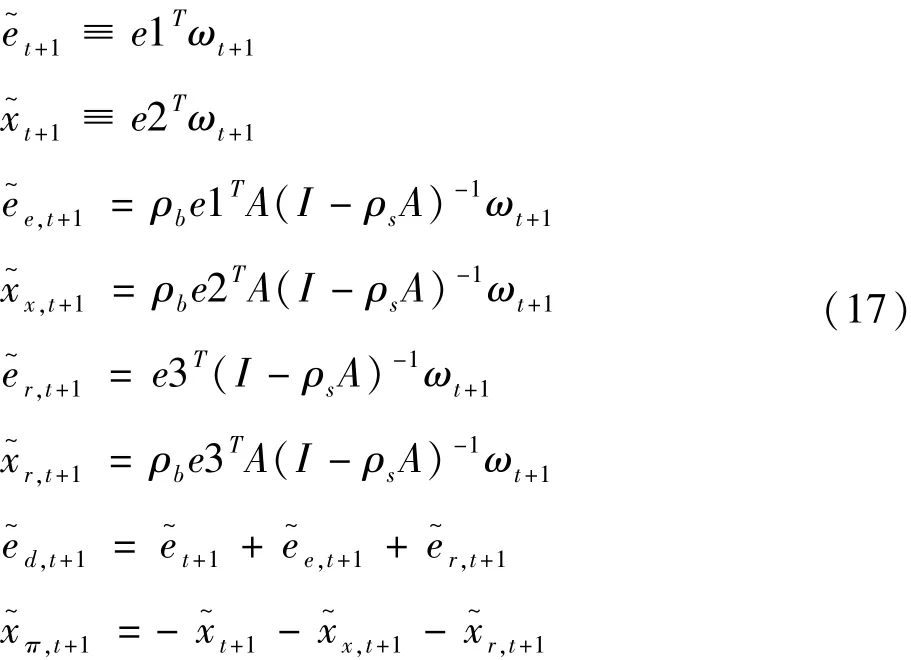
（三）多元回归

1.回归模型。

为了具体研究股票波动性和债券波动性的关系，并检验二者的联动性是否会受到二者波动性的影响，我们设计三个多元回归方程来进行因素影响分析。其中，等式左边为通过前文中向量自回归的相关数据计算出来的企业股票非预期超额收益率波动率var(）、企业债券非预期超额收益率波动率 var(），以及二者的相关系数corr(，），这三个指标分别作为三个方程的因变量，自变量除了选取主要研究的债券及股票超额收益波动率之外，根据已有文献的贡献选取了与股债关系较为密切的两个宏观变量，分别为通货膨胀率π和反应货币流动性的货币供应量m2与国民生产总值gdp之比mgdp。另外选取了三个微观变量，分别为债券市场波动率bf，股票市场波动率sf，以及股票换手率st。由于分别代表股票市场行情和债券市场行情的沪深300指数和中债全价指数均表现出明显的聚簇效应，我们通过GARCH模型消除并拟合得到两个市场的波动率数据。

2.GARCH拟合市场波动率序列。

代表股票市场和债券市场整体行情的常用指数分别为沪深300指数和中债全价指数，这两个指标的收益率序列通常情况下会出现在某个时间段变化波动幅度大，在另一个时间段变化波动幅度又比较小，会导致较大预测误差聚集在某一时间段，较小误差聚集在另一时间段的所谓聚类现象，因此选用GARCH模型来分析条件方差的变化规律，并拟合出波动率序列。

首先用方程（21）确定原始序列的均值方程，其阶数n可以用自相关函数、偏自相关函数、Ljung⁃Box统计量来确定，各参数可以用OLS求得。

其次，将方程（21）拟合得到的回归方程提取残差序列，若残差序列呈现自相关性，或在残差与时间的变化关系图上观察到聚类现象，则意味着ARCH现象的存在，最后，对残差建立GARCH(p，q）模型，如方程（22）所示，对原均值方程的回归结果进行修订。其中ht=bf或sf。

四、实证结果

（一）数据来源及变量定义

考虑到宏观变量的可获得性，将选取季度频率数据，为保证实证结果的可靠性，在选取数据时，剔除信息特异以及数据缺失的企业，最终获取本文实证分析的样本，2012—2016年A股市场中103家上市企业相关数据。其中股票收盘价SP、债券收盘价BP数据、股利D、股票换手率st、国债收益率y、实际利率r、国民生产总值GDP、货币供应量M2、沪深300指数HS和中债指数ZZ数据来源于wind数据库和大智慧数据库，收益率数据均为根据收盘价或指数通过对数收益率方法计算得出，股票市场波动率sf和债券市场波动率bf通过沪深300指数收益率和中债指数收益率的GARCH模型拟合得到。综合前文所涉及到的变量，表1给出具体的描述和变量符号。

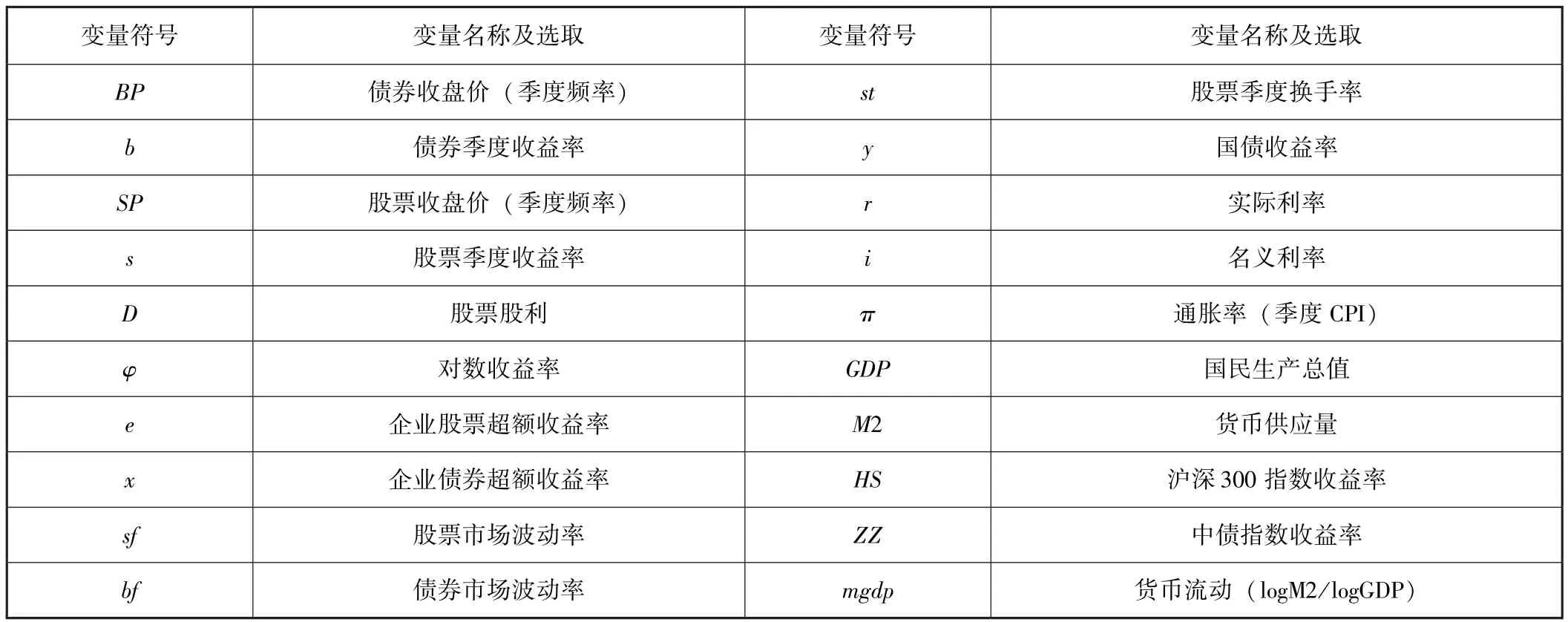
表1 变量定义及简单描述

（二）描述性统计分析

表2为涉及到的微观变量的描述性统计分析，表3为涉及到的宏观变量的描述性统计分析。从数据看来，无论是股票价格SP标准差（6.788）、股票收益率s标准差（10.052）还是企业股票超额收益率e标准差（10.021）均分别大于债券价格BP标准差(4.867）、债券收益率b标准差（1.441）以及企业债券超额收益率x标准差（1.719），这与实际经济中，股票市场波动性明显大于债券市场波动性是相符的，此外沪深300指数HS和中债全价指数ZZ标准差（43 544.120和356.054）较高，考虑两个市场的波动行情是否会影响股债联动特征也是有必要的。

表2 微观变量的描述性统计分析

表3 宏观变量的描述性统计分析

（三）平稳性检验

表4描述了各变量的ADF测试的结果，结果显示企业股票超额收益率e，企业债券超额收益率x，实际利率r、对数收益率φ和名义利率一阶差分序列Δi的pp检验统计量对应的P值均小于5%的显著性水平，因此各变量均为平稳的时间序列，保证了这五个变量的向量自回归的可实施性。此外股票换手率st、通胀率π、国民生产总值的对数值gdp以及货币供应量对数值m2的平稳性测试结果显示四个变量的pp检验统计量均大于在5%显著性水平下的临界值，即P值均小于5%显著性水平，表明四个序列均是平稳的时间序列，因此进行回归时不会出现 “虚假回归”现象。

表4 变量的平稳性检验

（四）相关性检验

表5为向量自回归中变量的相关性结果：从表5中可以看出，企业股票超额收益率e与企业债券超额收益率x相关系数为-0.008，初步看出我国两大证券市场股票市场和债券市场间的关联度不高，可能会显示出较低的联动性。表中显示不可避免的实际利率r与企业债券超额收益率x表现较高的相关系数-0.546，除此之外其余各变量的相关系数均较小，因此进行回归不会出现多重共线性问题。

表5 变量的相关性检验

（五）VAR回归结果

首先，我们对方程（12）进行自回归，根据拟合优度比较，同时便于长短期进行对比，本文选取了滞后两期的向量自回归模型。表6报告了实证结果，整体来看，向量自回归的每个方程拟合优度在接受范围内。此外可以看出，第一个方程中，企业债券超额收益率对企业股票债券超额收益率，无论滞后一阶还是滞后二阶，其t检验统计量的值（2.293和4.354）均明显大于临界值2，且系数均为正（0.362和0.689），表明债券对股票的有显著的正的影响力。而在第二个方程中，企业股票超额收益率对企业债券超额收益率的影响，无论滞后一期还是滞后二期，其t检验统计量（-0.003和-0.004）均明显小于临界值，表明股票对债券的影响并不显著。从向量自回归结果中也可进一步判断股债之间具有非对称的影响力。

表6 VAR回归结果

续前表

（六）收益分解结果及分解因子相关性

将向量自回归的结果代入方程（15）～(17）所得结果如表7所示，各分解因子的相关性如表8所示。表7中收益分解结果数据结果显示，我国证券市场中，企业股票非预期超额收益波动主要来源于未来分红信息（短期74.360和长期72.654），债券市场中，通货膨胀信息为企业债券非预期超额收益的波动贡献最大，短期为1.840长期为1.833。这一点与Campbell(1991）[1]在美国市场的发现以及Tom Engst⁃ed(2001）[2]在丹麦市场的结果是一致的。

表8展示了各分解因子之间的相关系数关系，由表8可知，企业股票非预期超额收益率与企业债券非预期超额收益率的相关系数（0.090）较小，表明我国两大证券市场整体上不具有明显的联动性。同时也可看出，未来分红信息与股票非预期超额收益的高关联性（0.994和0.972）和通货膨胀信息与债券超额收益的高负相关性（0.997和0.986），且随着期限延长，这两种关联性均略有下降。此外分红信息对债券超额收益以及未来债券预期收益具有正的相关系数(0.097和0.274），而通货膨胀信息对超额股票收益以及未来股票预期收益也是一个坏的消息。

表7 收益分解结果

表8 分解因子相关性

（七）GARCH拟合结果

通过ARMA模型拟合方程（21）和GARCH(1，1）模型拟合方程（22）可以得到债券市场波动率bf和股票市场波动率sf的序列如下：

（八）多元回归结果

方程（18）～(20）的回归结果如下表9所示。从表9可以看出，方程（18）中，企业债券非预期超额收益波动Var和债券市场波动性bf对企业股票非预期超额收益波动Vare～的回归系数分别为0.689和1 098.623，即具有正效用，且均通过1%的显著性水平。表明在99%的可信度下，我们可以认为债券市场波动对股票市场波动有显著的正的影响力，也就是说债券市场波动增加，会引起股票市场的波动。另外宏观变量中，通货膨胀率π和货币流动性mgdp均通过了1%显著性水平的系数显著性检验，对股票市场的波动有正的影响力。

而在方程（19）中，企业股票非预期超额收益率波动Vare～对企业债券非预期超额收益率波动Var的影响虽显著，但系数仅有0.016，效用较小，并且股票市场波动sf以及反应股票市场流动性的股票换手率st对企业债券超额收益波动的系数均未通过5%的显著性检验，即对债券波动未产生显著的影响。宏观变量中，货币流动性mgdp对债券波动体现出显著正效用，而通货膨胀率π对债券超额收益波动体现出显著的负效用。

从以上两个方程中可以进一步得出结论，股票市场对债券市场的影响较为微弱甚至不显著，而债券市场波动对股票市场的波动具有显著的正相关性，即债券的波动会加剧股票市场的波动，说明我国股票市场和证券市场的非对称联动性。

对于方程（20），我们考虑了股债相关性的影响因素，从结果看来，股票非预期超额收益波动对股债相关性具有显著正影响，也就是说，股票市场的波动会增强股债相关性，而债券非预期超额收益波动对股债相关性影响不显著，此外宏观变量均对股债相关性没有显著的影响，这一点可能是由于股票和债券之间本身的弱相关性导致。

表9 多元回归结果

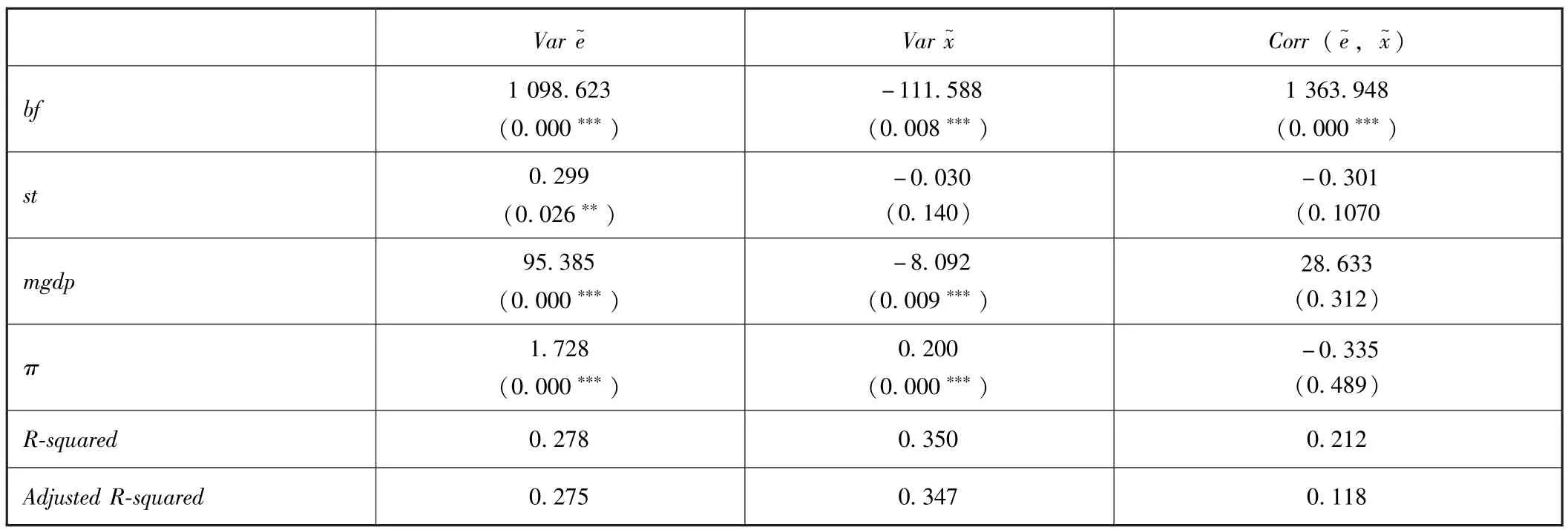
注:∗代表系数通过10%显著性水平,∗∗代表系数通过5%显著性水平,∗∗∗代表系数通过1%显著性水平。

五、结论及建议

本文首先通过线性估计资产定价模型进行股票超额收益和债券超额收益的方差分解，其次运用向量自回归模型所得到的残差来对股票非预期超额收益表达式和债券非预期超额收益表达式的各分解因子进行估计和计算，最后通过多元回归模型探究股债联动的非对称性特征及影响股债相关性的因素，其中包括宏观因素如货币流动性和通货膨胀率以及微观因素如市场指数波动率和换手率。

基于我国A股市场中103家同时拥有债权融资和股权融资两种方式的上市企业，其2012年—2016年季度股票和债券收益数据的实证分析，得到的结果表明：第一，股票收益波动与债券收益波动的相关性较小，也就是说债券市场和股票市场整体联动性较弱，其中一个市场的波动引起的另一个市场的波动幅度较小，表明我国证券市场中存在一定的市场分割性；第二，企业债券超额收益波动和债券市场指数的波动对企业股票超额收益波动会造成显著的正效应，即债券波动信息增加是导致股票非预期收益的增加的原因之一，相反，股票市场指数及股票市场流动性对企业债券的超额收益波动却没有体现出显著的影响，也就是说股票市场中的信息没有产生对债券市场的溢出效应，不会显著引起债券市场的波动变化，因此可以看出我国债券市场和股票市场表现出一种非对称的联动溢出效应；第三，企业股票超额收益波动的增加会增强股债相关系数，而企业债券超额收益波动对股债相关系数并未表现出显著的影响，同时，宏观因素中货币流动性和通货膨胀率虽都单独对股票市场和债券市场分别产生显著作用，但对股票债券的相关系数的影响是不显著的，这一点可能也体现了股债之间的弱相关性。

从结论中可以看出我国证券市场中，股债联动性整体较弱且表现出非对称的溢出效用，并且与股票市场相比，债券市场的流动性和活跃度都稍显逊色，因此为促进证券市场的健康发展和提高市场运行效率，国家和资本市场相关部门应加快完善证券市场的相关政策法规，大力发展债券市场，完善资本市场结构，加强监管，减弱市场间的非对称效应，从而减少通过市场间非对称状态来牟取暴利和操纵市场的行为，增强证券市场的有效性。

[1]Campbell，J.Y.，and R.J.Shiller.The Dividend⁃Price Ratio and Expectations of Future Dividends and Discount Factors[J].Review of Financial Studies，1988(1）：195-228.

[2]Tom Engsted，Carsten Tanggaard.The Danish Stock and Bond Markets：Comovement，Return Predictability and Variance Decomposition[J].Jour⁃nal of Empirical Finance，2001(8）：243-271

[3]王璐，黄登仕.分割市场下中国股票市场和债券市场联动特征研究 [J].金融理论与实践，2015(7）：15-21.

[4]郑振龙，陈志英.中国股票市场和债券市场收益率动态相关性分析 [J].当代财经，2011(2）：45-53.

[5]韩学红，郑妍妍，伍超明.对我国股票收益率与通货膨胀率关系的解释：1992—2007[J].金融研究，2008(4）：21-36.

[6]罗荣华，门明，吴锟.我国股票市场和债券市场联动的非线性动态分析 [J].中央财经大学学报，2014(3）：39-46.

[7]曾志坚，江洲.关于我国股票市场与债券市场收益率联动性的实证研究 [J].当代财经，2007(9）：58-64.

[8]Campbell，J.Y，John Ammer.What Moves the Stock and Bond Markets，A Variance Decomposition for Long⁃Term Asset Returns[J].The Journal of Finance，1993，48(1）：3-37.

[9]Nektarios Aslanidis，Charlotte Christiansen.Smooth Transition Patterns in the Realized Stock⁃bond Correlation[J].Journal of Empirical Finance，2012(15）：454-464.

[10]Bharat Kolluri，Susan Machuga，Mahmoud Wahab.Co⁃Movements of US and Asian Equity Markets：Evidence from Asymmetric and Time⁃Varying Coefficients[J].Review of Pacific Basin Financial Markets＆ Policies，2014，17(4）：251-171.

[11]徐林.我国股市与债市（国债）相关性研究 [D].西南财经大学，2006.

[12]刘大明.中国股票与债券市场价格联动研究 [D].首都经济贸易大学，2012.

[13]陈学彬，曾裕峰.中美股票市场和债券市场联动效应的比较研究——基于尾部风险溢出的视角 [J].经济管理，2016，(07）：1-13.

[14]Tom Engsted，Carsten Tanggaard.The comovement of US and German bond markets[J].International Review of Financial Analysis，2007(16）：172-182.

[15]Campbell，J.Y.A Variance Decomposition for Stock Returns[J].Economic Journal，1991(101）：57-179.

[16]Tom Engsted，Thomas Q，Pedersen，Carsten Tanggaard.Pitfalls in VAR Based Return Decompositions，A clarification[J].Journal of Banking ＆Finance，2012(36）：1255-1265.

[17]Lieven Baele，Geert Bekaert and Koen Inghelbrecht.The Determinants of Stock and Bond Return Comovements[J].The Review of Financial Stud⁃ies，2010，23(6）：2374-2428.

[18]Jian Yang，Yinggang Zhou and Zijun Wang.The Stock⁃bond Correlation and Macroeconomic Conditions[J].Journal of Banking ＆ Finance，2009(33）：670-680.

[19]Ruslan Y.Goyenko，Andrey D.Ukhov.Stock and Bond Market Liquidity：A Long⁃Run Empirical Analysis[J].The Journal of Financial and Quantitative Analysis，2009，44(1）：189-212

[20]曾志坚，罗长青.股票与债券市场流动性联动的实证研究 [J].财经理论与实践，2008(4）：45-49.

[21]荚超强.基于VAR模型的资产市场规模与通货膨胀的关联性研究 [J].巢湖学院学报，2015(2）：24-30.

[22]张小双.多市场协同作用与股票市场的联动关系研究 [D].哈尔滨工业大学，2014.

[23]王媛，李帆.股票市场与债券市场的相关性研究 [J].武汉理工大学学报（信息与管理工程版），2014(2）：265-269.

[24]范原源.关于股票市场和债券市场收益率联动特征的研究 [D].西南财经大学，2014.

[25]周迪.我国债市与股市不同板块收益率相关性研究 [D].复旦大学，2014.

[26]丁春辉.关于中美国债市场联动性及其影响因素的实证分析 [D].厦门大学，2014.

[27]王晴.基于BVAR模型的股债联动关系实证研究 [D].上海交通大学，2014.

[28]孙乾祐.中国股票市场与债券市场的收益率联动关系研究 [D].东北财经大学，2013.

[29]戴月.我国创业板与国内主板、中小板的联动关系研究 [D].上海师范大学，2013.

[30]郑劲.基于VAR(P）⁃MGARCH⁃BEKK模型的我国股市和债市的收益率和波动率溢出研究 [D].南京大学，2013.

[31]史永东，丁伟，袁绍锋.市场互联、风险溢出与金融稳定——基于股票市场与债券市场溢出效应分析的视角 [J].金融研究，2013(3）：170-180.

[32]高江.中国与国际债券市场收益特征及联动性研究 [J].上海财经大学学报，2012(6）：68-74.

[33]栾珺.基于Copula模型的中国股票和债券市场联动性研究 [D].东北财经大学，2012.

[34]刘子威.中国股票市场与世界主要股票市场联动效应分析 [D].西南财经大学，2012.

[35]赵博.国内外股票市场联动性研究 [D].西南财经大学，2012.

[36]黄琼.信贷经济与世界货币危机的关系研究 [J].统计与决策，2010(24）：149-151.

[37]陆贤伟.中国债券与股票市场间收益波动非对称研究 [D].西南交通大学，2010.

[38]胡秋灵，刘伟.中美股市联动性分析——基于次贷危机背景下的收益率研究 [J].金融理论与实践，2009(6）：79-84.

[39]苗国伟.我国股票市场和债券市场联动关系研究 [D].中国海洋大学，2009.

[40]骆振心.金融开放、股权分置改革与股票市场联动——基于上证指数与世界主要股指关系的实证研究 [J].当代财经，2008(4）：52-57.

[41]袁超，张兵，汪慧建.债券市场与股票市场的动态相关性研究 [J].金融研究，2008(1）：63-75.

[42]陈梦根，曹凤岐.中国证券市场价格冲击传导效应分析 [J].管理世界，2005(10）：24-33.

[43]张昱.用向量自回归和方差分解研究股票收益波动的影响因素 [D].重庆大学，2005.

[44]雷倩华，盈余质量与我国股票收益波动——基于我国股票收益VAR方差分解的实证分析 [J].金融评论，2015(1）：78-80.