基于社会网络的民航旅客影响力计算
李陇豫
(中国民航大学 中欧航空工程师学院,天津 300300)
现有的影响力度量方法主要有基于网络拓扑结构[1-2]、基于用户行为[3-4]和基于用户交互行为[5]的影响力度量方法。本文根据民航旅客订座数据(Passenger Name Record,简称为“PNR”),基于民航旅客社会网络拓扑结构和旅客共同出行行为,提出一种民航旅客影响力的度量方法。
1 基于网络结构的旅客影响力度量方法
PageRank算法是一种基于链接结构的网页排名算法,该算法通过网页之间的链接关系对网页的重要性作出评判。PageRank算法的数学公式如下:
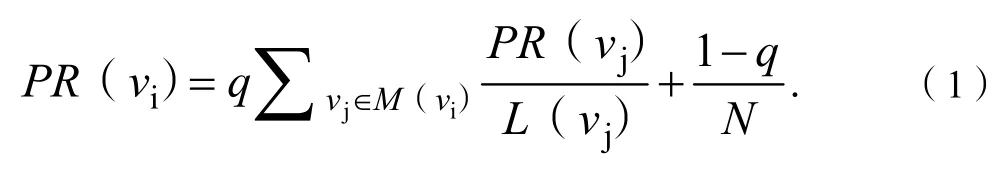
式(1)中:PR(vi)为网页vi的PageRank值;PR(vj)为链接到网页vi的网页vj的PageRank值;L(vj)为网页vj包含的链接数量;q为对网络中所有页面公平引入的阻尼系数。
由于民航旅客社会网络是一个有向加权的社会网络,PageRank算法中对初始权重平均分配并不合理,因此我们利用改进后的PageRank算法来计算网络中节点的影响力大小。改进后节点PR值的计算公式如下:
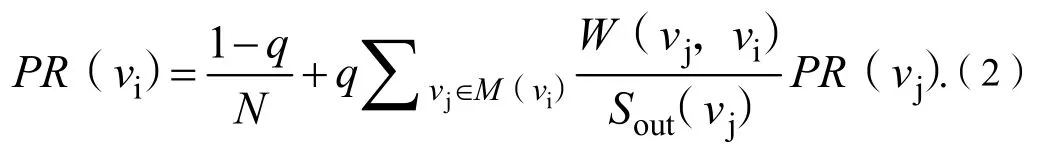
式(2)中:W(vj,vi)表示节点vj对节点vi的影响强度;Sout(vj)表示节点vj的出强度,其计算公式为:

由此,我们得到了网络中所有节点基于网络拓扑结构的影响力大小。
2 基于旅客出行行为的旅客影响力度量方法
每名旅客与其他旅客的共同出行行为对该旅客自身的影响力也有一定程度的影响,若一名旅客与其他旅客共同乘机的次数越多、频率越高,则该旅客越容易对其他旅客产生影响,则其自身的影响力也就越大。因此,度量旅客影响力时需要考虑该旅客与其他旅客的共同出行行为。本文使用旅客共同出行的次数和共同出行的频次来量化旅客vi,vj之间的共同出行行为,具体计算方法如式(4):
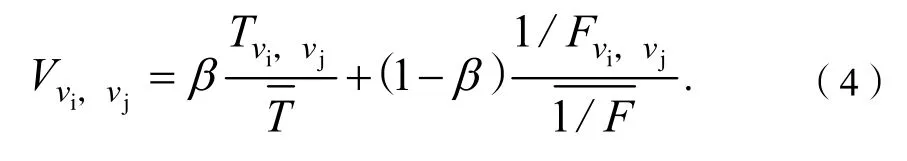
式(4)中:Tvi,vj和Fvi,vj分别表示旅客vi,vj在一段时间内的共同出行次数和旅客vi,vj最近一次出行日期与统计日期的间隔天数;和分别表示网络中所有旅客间的共同出行次数和出行频次的平均值;β为旅客共同出行次数和频次的调节因子。因此,我们得到旅客vi的平均共同出行量为:
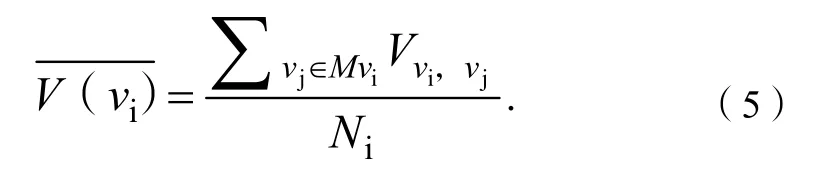
式(5)中:ivM表示旅客vi的邻居节点集合;Ni为旅客的
2.1.1 政府要大力发展农村经济。政府要立足于社会的发展,发展农村经济,农村经济有了政府政策的倾斜,可以反哺农村空巢老人生活环境的改善,使其为空巢老人在内所有老人的晚年生活提供经济保障。这样不仅可以缓解城市的就业压力,而且可以吸引外出工作的子女返乡,让空巢老人真正实现“老有所依”。
邻居节点个数,
综合民航旅客社会网络的网络拓扑结构和旅客的出行行为,我们得到民航旅客影响力计算模型CAPI-Rank如式(6)所示:

式(6)中:α为基于网络拓扑的旅客影响力和基于旅客出行行为的影响力的平衡因子,0≤α≤1.
3 实验
3.1 实验数据与实验环境
本文采用节点数为2 034、边数为13 328的民航旅客社会网络进行实验验证。实验的硬件环境为Inter(R)Core(TM)i5-2400 CPU@3.10 GHz×4,4 GB内存。
3.2 实验流程及评价指标
本文通过IC模型模拟旅客影响力的传播,将每个旅客最终激活的节点数作为他们真实的影响力值。由于民航旅客社会网络模型的间边权重表示旅客之间的影响强度,因此这里我们用网络中的边权重作为IC模型中的激活概率p.
将本文提出的CAPI-Rank影响力度量方法与度中心性DC、接近中心性CC、介数中心性BC和PageRank算法4种常用的影响力度量方法进行对比,采用斯皮尔曼相关系数ρ来衡量不同度量方法得出的旅客排名与真实旅客影响力排名的相关性。
3.3 实验参数选择
CAPI-Rank模型中共有α,β两个参数,α用来调节网络拓扑结构和旅客出行行为对影响力的影响,β用来调节旅客出行行为中出行次数和出行频次的比例。下面通过实验讨论两个参数的取值问题。
图1展示了CAPI-Rank模型在不同α,β下的变化情况。从图中可以看出,CAPI-Rank模型在α=0.765、β=0.824时取得最大值。
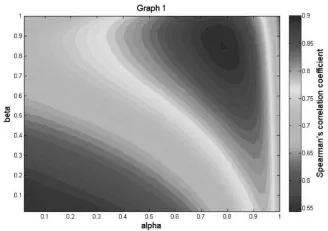
图1 不同参数取值CAPI-Rank模型ρ值变化情况
3.4 实验结果及分析
在得到CAPI-Rank中的最优参数α,β后,我们通过实验比较了CAPI-Rank和度中心性DC、接近中心性CC、介数中心性BC、PageRank算法的表现。
图2为5种度量方法在民航旅客社会网络下的ρ值。从图中我们可以看出,CAPI-Rank相比于其他度量方法能取得最大的ρ值,说明CAPI-Rank在该网络中能够取得最好的度量效果。由于网络中节点连接不紧密,并且节点之间的影响强度很小,节点的影响力很难在网络中传播开来,大多数节点只能影响网络中与它相近的小部分节点。正因为如此,DC的效果相对较好,因为DC仅按照网络中节点的度数排序,能够找到不同区域内影响力相对较大的节点;而CC考虑网络中节点与其他节点之间的路径长短,但事实上,处于网络中心的节点由于影响强度的限制很难将其影响力扩散开,因此CC的效果并不理想。而CAPI-Rank模型由于考虑可网络拓扑和旅客出行行为两方面的因素,在最终结果上要优于仅考虑网络拓扑结构的度量方法。

图2 不同度量方法在民航旅客社会网络下的ρ值
4 总结
本文根据民航旅客订座数据的特点,基于网络拓扑结构和旅客共同出行行为,提出了一种旅客影响力的计算模型。实验表明,本文提出的CAPI-Rank模型在民航旅客影响力度量准确性方面要优于传统的影响力度量方法。
[1]Page L,Brin S,Motwani R,et al.The PageRank citation ranking:Bringing order to the web[J].Food Microstructure,1999(01):1-17.
[2]金迪,马衍民.PageRank算法的分析及实现[J].经济技术协作信息,2009(18):118.
[3]Rabiger S,Spiliopoulou M.A framework for validating the merit of properties that predict the influence of a twitter user[J].Expert Systems with Applications,2015,42(5):2824-2834.
[4]毛佳昕,刘奕群,张敏,等.基于用户行为的微博用户社会影响力分析[J].计算机学报,2014,37(4):791-800.
[5]史艳翠,杨巨成,陈亚瑞,等.基于移动数据的用户间影响力计算方法[J].华中科技大学学报,2017,45(7):110-114.
[6]张琨,李配配,朱保平,等.基于PageRank的有向加权复杂网络节点重要性评估方法[J].南京航空航天大学学报,2013(03):429-434.

