基于回转半径法的任务定价和完成度分析研究

陈茂林，张 雷，范泽华，崔雅洪

（重庆交通大学，重庆 080605）

随着互联网的快速发展和网民的不断增加，电子商务蓬勃崛起。在这一形势下，外包的出现使交易模式发生巨大的改变。电子商务掀起一番热潮，众包随之引起社会各界的关注。“拍照赚钱”就是一种自助服务模式。用户下载相应APP后注册，在APP上自助领取任务，完成任务后赚取任务标定金额。对比传统的市场调查，不仅有效降低了成本，而且保证了调查的真实性，但随之而来的便是任务定价和完成度的问题。

1 模型的建立

1.1 任务位置与会员位置之间的距离

先用Excel软件将任务标价为65的所有任务筛选出来，将这些数据与会员信息放在同一表格内。计算这些筛选数据中的每个任务位置与所有会员位置的距离，公式如下：

式（1）中：l为任务位置与会员位置的距离；（xi，yi）（xj，yj）分别为任务位置与会员位置。

将所得的所有距离从小到大进行排列。

1.2 定价半径

当会员成本大于收益，任务几乎为不可能完成。因此，我们规定会员愿意接受距离其在30 km以内的任务，并且规定定价半径的范围是（15，30）。用回转半径法求解定价半径，应用在这里的回转半径法是指以会员位置（xj，yj）为中心做标准圆，以任务位置与会员位置的距离l为半径，不断变化任务位置与会员位置的距离l，观察会员在不同半径范围内的分布状况，进而得到会员在空间上的分布特征。运用MATLAB软件画出会员个数与任务位置与会员位置的距离对应的空间分布曲线，求解会员在空间上的分布特点。

分析任务标价为65的65组数据。在（15，30）内，用二分法不断缩小定价半径的范围，取得最优值。最后得定价半径的最优值为19 km。

1.3 会员密度

根据任务位置的分布可以得出，任务标价为80，85时，离会员集中分布的区域较远。在不考虑标价的影响下，令A～U分别为任务标价为65～75中任务的集合。

对于A集合中的65个项目而言，以19 km为定价半径，分别得到圆内的会员个数。取区域会员个数的均值作为任务标价为65时圆内的会员个数，公式如下：式（2）中：（n=1，2，…，21）为集合A～T的圆内的会员个数，Nai表示A集合中各个项目的圈内会员个数。

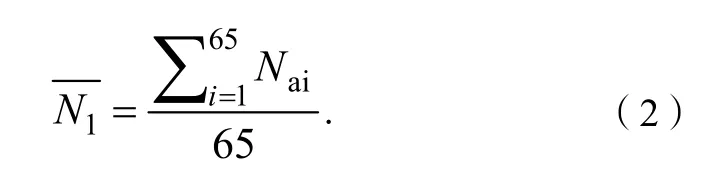
任务标价为65～75时，会员密度为：

式（3）中：ρn（n=1，2，…，20）为集合A～T会员密度；r为定价半径。

1.4 定价模型

用SPSS拟合出任务定价P与会员密度ρ之间的关系，即定价模型为p=88.197ρ2－70.058ρ+78.497.

1.5 任务未完成原因

首先根据题目所给中的数据，0为任务未完成，1为任务完成。将相应的GPS经纬度转化具体位置，发现几乎所有数据都集中在广东的4个城市，分别为佛山市、深圳市、广州市和东莞市，如表1所示。

表1 四个城市的任务完成情况

观察数据可知，未完成的项目都分布在佛山市、深圳市和广州市三座城市，而在东莞的项目全部完成任务。

将任务未完成的数据筛选出来，求出每个数据的会员密度为：

式（4）中：ρi（i=1，2，…，795）为所以未完成项目的会员密度；r为定价半径。

将所得ρi（i=1，2，…，795）与任务标价相等时的ρn（n=1，2，…，20）进行比较，当ρi＜ρn时，不符合定价规律；当ρi＞ρn时，符合定价规律。发生这两种情况的个数分别占总个数μ的比例为：

2 结果分析

2.1 定价模型的结果分析

由上述推导过程得出任务定价p与会员密度ρ之间的关系为p=88.197ρ2－70.058ρ+78.497.由模型可知，附件一中的定价规律为：任务定价p随着会员密度ρ的增大而减小，即人员越密集的地方，任务定价越低。符合现实情况，当一个任务的附近存在很多的会员，就会有越多的人来完成这个任务，这个任务被完成的可能性就会非常大，所以，定价低时也能完成一定的任务；相反，一个任务附近的会员个数特别少，则来领这个任务的人就少，随之任务完成率降低。因此，应以更高的任务定价来吸引会员，以提高这些任务的完成率。

2.2 对任务未完成原因的结果分析

从未完成数据中分析得按照定价原则分析：当ρi＜ρn时，不符合定价规律，这种情况是任务标价相同，未完成的人员密度小于平均的人员密度，人比规定的要少，价格却与规定的一样，所以，此时的任务未完原因是价格的不合理；当ρi＞ρn时，符合定价规律，这种情况是任务标价相同，未完成的人员密度大于平均的人员密度，人比规定的要多，价格却是一样的，这种情况的会员占优势，所以，此时的价格是高于同水平的人员密度所对应的价格。

查相关资料得知这45%的点所处地理位置的消费物价指数（CPI）高于附近的其他地区。所以，任务未完成的原因是所给出的价格相对他们日常生活中的CPI是不合理的，不够满足他们对佣金的最低需求水平。

综上所述，在未完成的项目中，55%的原因是因为任务定价的不合理，剩下45%是因为当地的CPI过高。

3 模型检验

运用Excel软件对定价模型进行回归分析，得到相关数据如表2所示。

表2 定价模型的回归分析

从表2可以看出，代表任务单价P与会员密度ρ拟合程度的R2=0.926，非常接近于1，所以p=88.197ρ2－70.058ρ+78.497能够充分地表达定价规律。

4 结束语

本文以会员密度建立定价标准，能够很好地满足大多数任务点的定价要求。该定价模型取各个任务项目圈内平均值作为相应标价代表性的会员个数，所求得代表性会员个数并不能满足全部的项目。针对该方面不足可以依照第30位最高小时交通量原则，满足80%的项目。即将一个标价内的所有项目的圈内会员个数从大到小排列，取占总数第20%的数据为代表会员个数方向进行改进。

［1］彭放，杨瑞琰.数学建模方法［M］.北京：科学出版社，2012.

［2］赵明，吴必虎.城市周边度假地空间区位研究——基于北京城市中心距离变化的思考［J］.重庆师范大学学报（自然科学版），2010，27（01）：74-75.

［3］柴宗政.基于相邻关系的森林空间结构量化评价及R语言编程实现——以秦岭中山带典型次生林为例［D］.咸阳：西北农林科技大学，2016.